f-число
Число f является мерой способности оптической системы, такой как объектив камеры, собирать свет. Оно вычисляется путем деления фокусного расстояния системы на диаметр входного зрачка («чистая апертура »). [1] [2] [3] Число f также известно как фокусное отношение , f-ratio или f-stop , и оно играет ключевую роль в определении глубины резкости , дифракции и экспозиции фотографии. [4] Число f является безразмерным и обычно выражается с помощью строчной буквы f с крючком в форматеж /N , где N — диафрагменное число.
Число f также известно как обратная относительная апертура , потому что это величина, обратная относительной апертуре , определяемой как диаметр апертуры, деленный на фокусное расстояние. [5] Относительная апертура показывает, сколько света может пройти через объектив при заданном фокусном расстоянии. Меньшее число f означает большую относительную апертуру и больше света, попадающего в систему, в то время как большее число f означает меньшую относительную апертуру и меньше света, попадающего в систему. Число f связано с числовой апертурой (NA) системы, которая измеряет диапазон углов, в которых свет может входить или выходить из системы. Числовая апертура учитывает показатель преломления среды, в которой работает система, в то время как число f не учитывает.
Обозначение
Диафрагменное число N определяется по формуле:
где f - фокусное расстояние , а D - диаметр входного зрачка ( эффективная апертура ). Обычно числа f пишутся с предваряющим их символом "ж /", который формирует математическое выражение диаметра входного зрачка в терминах f и N. [ 1] Например, если фокусное расстояние линзы равно100 мм , а диаметр его входного зрачка был50 мм , число f будет равно 2. Это будет выражено как "ж /2" в системе линз. Диаметр апертуры будет равен f /2 .
Объективы камер часто включают регулируемую диафрагму , которая изменяет размер диафрагмы и , таким образом, размер входного зрачка. Это позволяет пользователю изменять число f по мере необходимости. Диаметр входного зрачка не обязательно равен диаметру диафрагмы из-за увеличительного эффекта линз перед апертурой.
Игнорируя различия в эффективности пропускания света, объектив с большим числом f проецирует более темные изображения. Яркость проецируемого изображения ( освещенность ) относительно яркости сцены в поле зрения объектива ( яркость ) уменьшается пропорционально квадрату числа f.Фокусное расстояние 100 ммж /4Линза имеет входной зрачок диаметром25 мм . АФокусное расстояние 100 ммж /2Линза имеет входной зрачок диаметром50 мм . Поскольку площадь пропорциональна квадрату диаметра зрачка, [6] количество света, пропускаемогож /2линза в четыре раза больше, чемж /4объектив. Чтобы получить ту же фотографическую экспозицию , время экспозиции должно быть уменьшено в четыре раза.
АФокусное расстояние 200 ммж /4Линза имеет входной зрачок диаметром50 мм .Входной зрачок объектива 200 мм имеет площадь, в четыре раза превышающую площадь100 мм ж /4входной зрачок линзы, и таким образом собирает в четыре раза больше света от каждого объекта в поле зрения линзы. Но по сравнению с100 мм объектив,Объектив с фокусным расстоянием 200 мм проецирует изображение каждого объекта в два раза выше и в два раза шире, охватывая в четыре раза большую площадь, и поэтому оба объектива создают одинаковую освещенность в фокальной плоскости при съемке сцены заданной яркости.
Остановки, условные обозначения диафрагмы и экспозиция


Слово «стоп» иногда сбивает с толку из-за его множественных значений. Стоп может быть физическим объектом: непрозрачной частью оптической системы, которая блокирует определенные лучи. Диафрагма — это настройка диафрагмы, которая ограничивает яркость изображения путем ограничения размера входного зрачка, в то время как полевая диафрагма — это диафрагма, предназначенная для отсечения света, который находится за пределами желаемого поля зрения и может вызвать блики или другие проблемы, если ее не остановить.
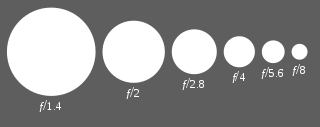
В фотографии стопы также являются единицей, используемой для количественной оценки соотношений света или экспозиции, причем каждая добавленная стопа означает коэффициент два, а каждая вычитаемая стопа означает коэффициент один в два раза. Единица в одну стопу также известна как единица EV ( значение экспозиции ). На камере настройка диафрагмы традиционно регулируется дискретными шагами, известными как f-стопы . Каждая « стопа » отмечена соответствующим ей числом f и представляет собой уменьшение вдвое интенсивности света по сравнению с предыдущей остановкой. Это соответствует уменьшению диаметров зрачка и диафрагмы в 1/ √ 2 или примерно на 0,7071, и, следовательно, уменьшению вдвое площади зрачка.
Большинство современных объективов используют стандартную шкалу диафрагмы, которая представляет собой приблизительно геометрическую последовательность чисел, соответствующую последовательности степеней квадратного корня из 2 : ж /1,ф /1.4,ж /2,диафрагма /2.8,ж /4,ж /5.6,ж /8,ж /11,ж /16,ж /22,ж /32,ж /45,ж /64,ф /90,ж /128и т. д. Каждый элемент в последовательности на одну ступень ниже элемента слева от него и на одну ступень выше элемента справа. Значения отношений округлены до этих конкретных условных чисел, чтобы их было легче запомнить и записать. Последовательность выше получена путем аппроксимации следующей точной геометрической последовательности:
Точно так же, как одна ступень диафрагмы соответствует двукратному увеличению интенсивности света, выдержки устроены так, что каждая настройка отличается по длительности примерно в два раза от соседней. Открытие объектива на одну ступень позволяет в два раза большему количеству света попасть на пленку за определенный период времени. Следовательно, чтобы получить ту же экспозицию при этой большей диафрагме, что и при предыдущей, затвор должен быть открыт на половину времени (т. е. на вдвое большую скорость). Пленка будет одинаково реагировать на эти равные количества света, поскольку она обладает свойством взаимности . Это менее верно для чрезвычайно длинных или коротких выдержек, где имеет место нарушение взаимности . Диафрагма, выдержка и чувствительность пленки связаны: для постоянной яркости сцены удвоение площади диафрагмы (одна ступень), уменьшение вдвое выдержки (удвоение времени открытия) или использование пленки в два раза более чувствительной оказывает одинаковое влияние на экспонируемое изображение. Для всех практических целей не требуется экстремальная точность (механические скорости затвора были печально известны своей неточностью, поскольку износ и смазка варьировались, не влияя на экспозицию). Не имеет значения, что площади диафрагмы и скорости затвора не изменяются ровно в два раза.
Фотографы иногда выражают другие соотношения экспозиции в терминах «стопов». Игнорируя маркировку числа f, значения f образуют логарифмическую шкалу интенсивности экспозиции. Учитывая эту интерпретацию, можно подумать о том, чтобы сделать полшага по этой шкале, чтобы получить разницу экспозиции в «полстопа».
Дробные остановки
Большинство камер двадцатого века имели плавно изменяющуюся апертуру с использованием ирисовой диафрагмы , с каждой отмеченной полной остановкой. Диафрагма с щелчком стала широко использоваться в 1960-х годах; шкала диафрагмы обычно имела щелчок на каждой целой и половинной остановке.
На современных камерах, особенно когда диафрагма установлена на корпусе камеры, f-число часто делится более мелко, чем шаги в одну ступень. Шаги в одну треть ступени ( 1 ⁄ 3 EV) являются наиболее распространенными, поскольку это соответствует системе светочувствительности пленки ISO . На некоторых камерах используются шаги в половину ступени. Обычно полные ступени отмечены, а промежуточные положения щелкают, но не отмечены. Например, диафрагма, которая на треть ступени меньше, чемдиафрагма /2.8являетсяж /3.2, на две трети меньшедиафрагма /3.5, и на одну целую остановку меньшеж /4. Следующие несколько значений диафрагмы в этой последовательности:
Для расчета шагов в полной остановке (1 EV) можно использовать
Шаги в серии полустопов ( 1 ⁄ 2 EV) будут следующими:
Шаги в третьей остановке ( 1 ⁄ 3 EV) серии будут следующими:
Как и в более ранних стандартах чувствительности пленки DIN и ASA, чувствительность ISO определяется только с шагом в одну треть ступени, а выдержки цифровых камер обычно имеют ту же шкалу в обратных секундах. Часть диапазона ISO представляет собой последовательность
в то время как выдержки в обратных секундах имеют несколько условных различий в своих числах ( 1 ⁄ 15 , 1 ⁄ 30 и 1 ⁄ 60 секунды вместо 1 ⁄ 16 , 1 ⁄ 32 и 1 ⁄ 64 ).
На практике максимальная апертура объектива часто не равна целой степени √ 2 (т. е. √ 2 в степени целого числа), в этом случае она обычно на половину или треть ступени выше или ниже целой степени √ 2 .
Современные сменные объективы с электронным управлением, например, те, что используются в зеркальных фотокамерах, имеют внутренние значения диафрагмы с шагом 1 ⁄ 8 ступени, поэтому настройки камеры в 1 ⁄ 3 ступени приблизительно соответствуют ближайшей настройке объектива в 1 ⁄ 8 ступени. [ необходима ссылка ]
Стандартная шкала диафрагменных чисел с полной остановкой
Включая значение диафрагмы AV:
Обычные и расчетные числа f, серия с полной остановкой:
| средний | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Н | 0,5 | 0,7 | 1.0 | 1.4 | 2 | 2.8 | 4 | 5.6 | 8 | 11 | 16 | 22 | 32 | 45 | 64 | 90 | 128 | 180 | 256 |
| рассчитано | 0,5 | 0,707... | 1.0 | 1.414... | 2.0 | 2.828... | 4.0 | 5.657... | 8.0 | 11.31... | 16.0 | 22.62... | 32.0 | 45,25... | 64.0 | 90,51... | 128.0 | 181.02... | 256.0 |
Типичная шкала диафрагменных чисел в полступени
| средний | −1 | − 1 ⁄ 2 | 0 | 1 ⁄ 2 | 1 | 1+1 ⁄ 2 | 2 | 2+1 ⁄ 2 | 3 | 3+1 ⁄ 2 | 4 | 4+1 ⁄ 2 | 5 | 5+1 ⁄ 2 | 6 | 6+1 ⁄ 2 | 7 | 7+1 ⁄ 2 | 8 | 8+1 ⁄ 2 | 9 | 9+1 ⁄ 2 | 10 | 10+1 ⁄ 2 | 11 | 11+1 ⁄ 2 | 12 | 12+1 ⁄ 2 | 13 | 13+1 ⁄ 2 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Н | 0,7 | 0.8 | 1.0 | 1.2 | 1.4 | 1.7 | 2 | 2.4 | 2.8 | 3.3 | 4 | 4.8 | 5.6 | 6.7 | 8 | 9.5 | 11 | 13 | 16 | 19 | 22 | 27 | 32 | 38 | 45 | 54 | 64 | 76 | 90 | 107 | 128 |
Типичная шкала диафрагменного числа в одну треть ступени
| средний | −1 | − 2 ⁄ 3 | − 1 ⁄ 3 | 0 | 1 ⁄ 3 | 2 ⁄ 3 | 1 | 1+1 ⁄ 3 | 1+2 ⁄ 3 | 2 | 2+1 ⁄ 3 | 2+2 ⁄ 3 | 3 | 3+1 ⁄ 3 | 3+2 ⁄ 3 | 4 | 4+1 ⁄ 3 | 4+2 ⁄ 3 | 5 | 5+1 ⁄ 3 | 5+2 ⁄ 3 | 6 | 6+1 ⁄ 3 | 6+2 ⁄ 3 | 7 | 7+1 ⁄ 3 | 7+2 ⁄ 3 | 8 | 8+1 ⁄ 3 | 8+2 ⁄ 3 | 9 | 9+1 ⁄ 3 | 9+2 ⁄ 3 | 10 | 10+1 ⁄ 3 | 10+2 ⁄ 3 | 11 | 11+1 ⁄ 3 | 11+2 ⁄ 3 | 12 | 12+1 ⁄ 3 | 12+2 ⁄ 3 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Н | 0,7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 | 36 | 40 | 45 | 51 | 57 | 64 | 72 | 80 | 90 |
Иногда одно и то же число включено в несколько шкал; например, отверстиеф /1.2может использоваться как в системе полустопа [7] , так и в системе одной трети стопа; [8] иногдаф /1.3иж /3.2и другие различия используются для шкалы одной трети остановки. [9]
Типичная шкала диафрагменного числа в одну четверть ступени
| средний | 0 | 1 ⁄ 4 | 1 ⁄ 2 | 3 ⁄ 4 | 1 | 1+1 ⁄ 4 | 1+1 ⁄ 2 | 1+3 ⁄ 4 | 2 | 2+1 ⁄ 4 | 2+1 ⁄ 2 | 2+3 ⁄ 4 | 3 | 3+1 ⁄ 4 | 3+1 ⁄ 2 | 3+3 ⁄ 4 | 4 | 4+1 ⁄ 4 | 4+1 ⁄ 2 | 4+3 ⁄ 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Н | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.7 | 1.8 | 2 | 2.2 | 2.4 | 2.6 | 2.8 | 3.1 | 3.3 | 3.7 | 4 | 4.4 | 4.8 | 5.2 | 5.6 |
| средний | 5 | 5+1 ⁄ 4 | 5+1 ⁄ 2 | 5+3 ⁄ 4 | 6 | 6+1 ⁄ 4 | 6+1 ⁄ 2 | 6+3 ⁄ 4 | 7 | 7+1 ⁄ 4 | 7+1 ⁄ 2 | 7+3 ⁄ 4 | 8 | 8+1 ⁄ 4 | 8+1 ⁄ 2 | 8+3 ⁄ 4 | 9 | 9+1 ⁄ 4 | 9+1 ⁄ 2 | 9+3 ⁄ 4 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Н | 5.6 | 6.2 | 6.7 | 7.3 | 8 | 8.7 | 9.5 | 10 | 11 | 12 | 14 | 15 | 16 | 17 | 19 | 21 | 22 | 25 | 27 | 29 | 32 |
H-стоп
Диафрагма H (от слова hole, по традиции пишется с заглавной буквы H) — это эквивалент числа f для эффективной экспозиции, рассчитанный на основе площади, охватываемой отверстиями в диффузионных дисках или ситчатой апертуре объективов Rodenstock Imagon .
Т-стоп
T -stop (для остановок пропускания, по соглашению пишется с заглавной буквы T) — это f-число, скорректированное с учетом эффективности пропускания света ( коэффициента пропускания ). Объектив с T-stop N проецирует изображение той же яркости, что и идеальный объектив с коэффициентом пропускания 100% и f-числом N. T-stop конкретного объектива, T , определяется путем деления f-числа на квадратный корень из коэффициента пропускания этого объектива: Например,f /2.0Объектив с коэффициентом пропускания 75% имеет T-стоп 2,3: поскольку реальные объективы имеют коэффициент пропускания менее 100%, число T-стоп объектива всегда больше его f-числа. [10]
При 8%-ных потерях на поверхность воздух-стекло на линзах без покрытия многослойное покрытие линз является ключевым фактором в конструкции линз для снижения потерь пропускания линз. Некоторые обзоры объективов измеряют T-стоп или скорость пропускания в своих эталонных тестах. [11] [12] T-стоп иногда используется вместо f-числа для более точного определения экспозиции, особенно при использовании внешних экспонометров . [13] Типичным является пропускание объективов 60%–95%. [14] T-стоп часто используется в кинематографии, где много изображений видны в быстрой последовательности, и даже небольшие изменения экспозиции будут заметны. Объективы кинокамер обычно калибруются в T-стопах вместо f-числа. [13] В неподвижной фотографии, без необходимости строгого соответствия всех используемых объективов и камер, небольшие различия в экспозиции менее важны; однако T-стоп все еще используется в некоторых видах специальных объективов, таких как объективы Smooth Trans Focus от Minolta и Sony .
Номера ASA/ISO
Чувствительность фотопленки и сенсора электронной камеры к свету часто указывается с помощью чисел ASA/ISO . Обе системы имеют линейное число, где удвоение чувствительности представлено удвоением числа, и логарифмическое число. В системе ISO увеличение логарифмического числа на 3° соответствует удвоению чувствительности. Удвоение или уменьшение чувствительности вдвое равно разнице в одну ступень T с точки зрения пропускания света.
Прирост

Большинство электронных камер позволяют усиливать сигнал, поступающий от приемного элемента. Это усиление обычно называется усилением и измеряется в децибелах. Каждый6 дБ усиления эквивалентны одному T-стопному значению светопропускания. Многие камкордеры имеют единый контроль над f-числом и усилением объектива. В этом случае, начиная с нулевого усиления и полностью открытой диафрагмы, можно либо увеличить f-число, уменьшив размер диафрагмы, при этом усиление останется нулевым, либо увеличить усиление, при этом диафрагма останется полностью открытой.
Правило «Санни 16»
Примером использования диафрагменных чисел в фотографии является правило солнечной шестнадцати : приблизительно правильная экспозиция будет получена в солнечный день при использовании диафрагмыж /16и выдержку, максимально близкую к обратной величине светочувствительности пленки ISO; например, при использовании пленки ISO 200 диафрагмаж /16и выдержку 1 ⁄ 200 секунды. Затем число f можно уменьшить для ситуаций с более слабым освещением. Выбор меньшего числа f означает «открытие» объектива. Выбор большего числа f означает «закрытие» или «закрытие» объектива.
Влияние на резкость изображения


Глубина резкости увеличивается с числом f, как показано на изображении здесь. Это означает, что фотографии, сделанные с низким числом f (большая диафрагма), будут иметь, как правило, объекты на одном расстоянии в фокусе, а остальная часть изображения (ближе и дальше элементы) вне фокуса. Это часто используется для фотографии природы и портретной съемки , поскольку размытие фона (эстетическое качество, известное как « боке ») может быть эстетически приятным и фокусирует зрителя на главном объекте на переднем плане. Глубина резкости изображения, полученного при заданном числе f, зависит также от других параметров, включая фокусное расстояние , расстояние до объекта и формат пленки или сенсора, используемых для съемки изображения. Глубину резкости можно описать как зависящую только от угла зрения, расстояния до объекта и диаметра входного зрачка (как в методе фон Рора ). В результате меньшие форматы будут иметь более глубокое поле, чем большие форматы при том же числе f для того же расстояния фокусировки и того же угла зрения , поскольку меньший формат требует меньшего фокусного расстояния (более широкоугольного объектива) для получения того же угла зрения, а глубина резкости увеличивается с более короткими фокусными расстояниями. Таким образом, эффекты уменьшенной глубины резкости потребуют меньших чисел f (и, следовательно, потенциально более сложной или сложной оптики) при использовании камер малого формата, чем при использовании камер большего формата.
Помимо фокусировки, резкость изображения связана с числом f через два различных оптических эффекта: аберрацию , вызванную несовершенной конструкцией линзы, и дифракцию , вызванную волновой природой света. [15] Оптимальное для размытия значение f-числа зависит от конструкции линзы. Для современных стандартных линз с 6 или 7 элементами наиболее резкое изображение часто получается околож /5.6–ж /8, в то время как для старых стандартных объективов, имеющих только 4 элемента ( формула Тессара ), останавливаясь наж /11даст самое резкое изображение. [ необходима цитата ] Большее количество элементов в современных объективах позволяет конструктору компенсировать аберрации, позволяя объективу давать более качественные снимки при меньших числах f. При малых диафрагмах глубина резкости и аберрации улучшаются, но дифракция создает большее рассеивание света, вызывая размытие.
Ослабление света также чувствительно к диафрагме. Многие широкоугольные объективы будут демонстрировать значительное ослабление света ( виньетирование ) по краям при больших диафрагмах.
У фотожурналистов есть поговорка: «ж /8и быть там », что означает, что быть на месте событий важнее, чем беспокоиться о технических деталях. Практически,ж /8(в форматах 35 мм и больше) обеспечивает достаточную глубину резкости и достаточную светосилу объектива для приемлемой базовой экспозиции в большинстве ситуаций дневного освещения. [16]
Человеческий глаз
Расчет числа f человеческого глаза включает расчет физической апертуры и фокусного расстояния глаза. Зрачок может быть открыт на 6–7 мм, что соответствует максимальной физической апертуре.
Число f человеческого глаза варьируется от примернож /8.3в очень ярко освещенном месте примерноф /2.1в темноте. [17] Расчет фокусного расстояния требует учета светопреломляющих свойств жидкостей в глазу. Рассмотрение глаза как обычной камеры и линзы, заполненных воздухом, приводит к неправильному фокусному расстоянию и числу f.
Фокусное отношение в телескопах

В астрономии f-число обычно называют фокусным отношением (или f-ratio ), обозначаемым как . Оно по-прежнему определяется как фокусное расстояние объектива , деленное на его диаметр или на диаметр апертурной диафрагмы в системе:
Несмотря на то, что принципы фокусного отношения всегда одинаковы, применение, к которому применяется этот принцип, может различаться. В фотографии фокусное отношение изменяет освещенность фокальной плоскости (или оптическую мощность на единицу площади изображения) и используется для управления такими переменными, как глубина резкости . При использовании оптического телескопа в астрономии не возникает проблемы глубины резкости, а яркость точечных звездных источников с точки зрения полной оптической мощности (не деленной на площадь) является функцией только абсолютной площади апертуры, независимой от фокусного расстояния. Фокусное расстояние управляет полем зрения прибора и масштабом изображения, которое представляется в фокальной плоскости на окуляре , пленочной пластине или ПЗС .
Например, 4-метровый телескоп SOAR имеет небольшое поле зрения (околож /16), что полезно для изучения звезд. Телескоп LSST 8,4 м, который будет охватывать все небо каждые три дня, имеет очень большое поле зрения. Его короткое фокусное расстояние 10,3 м (ф /1.2) стало возможным благодаря системе коррекции ошибок, которая включает в себя вторичные и третичные зеркала, трехэлементную рефракционную систему, а также активную установку и оптику. [18]
Уравнение камеры (G#)
Уравнение камеры, или G#, представляет собой отношение яркости, достигающей сенсора камеры, к яркости излучения в фокальной плоскости объектива камеры : [19]
где τ — коэффициент пропускания линзы, а единицы измерения указаны в обратных стерадианах (ср −1 ).
Рабочее число f
Число f точно описывает способность объектива собирать свет только для объектов, находящихся на бесконечном расстоянии. [20] Это ограничение обычно игнорируется в фотографии, где число f часто используется независимо от расстояния до объекта. В оптической конструкции часто требуется альтернатива для систем, где объект находится недалеко от объектива. В этих случаях используется рабочее число f . Рабочее число f N w определяется по формуле: [20]
где N — нескорректированное f-число, NA i — числовая апертура объектива в пространстве изображения , — абсолютное значение увеличения объектива для объекта, находящегося на определенном расстоянии, а P — увеличение зрачка . Поскольку увеличение зрачка редко известно, его часто принимают равным 1, что является правильным значением для всех симметричных линз.
В фотографии это означает, что при фокусировке ближе эффективная апертура объектива становится меньше, делая экспозицию темнее. Рабочее число f часто описывается в фотографии как число f, скорректированное для удлинения объектива с помощью коэффициента мехов. Это имеет особое значение в макросъемке .
История
Система чисел f для указания относительных апертур возникла в конце девятнадцатого века в конкуренции с несколькими другими системами обозначения апертуры.
Происхождение относительной апертуры
В 1867 году Саттон и Доусон определили "апертальное отношение" как, по сути, обратную величину современного числа f. В следующей цитате "апертальное отношение" " 1 ⁄ 24 " рассчитывается как отношение 6 дюймов (150 мм) к 1 ⁄ 4 дюйма (6,4 мм), что соответствуетж /24Диафрагма:
В каждой линзе есть, в соответствии с заданным апертурным отношением (то есть отношением диаметра диафрагмы к фокусному расстоянию), определенное расстояние близкого объекта от нее, между которым и бесконечностью все объекты находятся в одинаково хорошем фокусе. Например, в однообъективной линзе с фокусом 6 дюймов, с диафрагмой 1/4 дюйма (апертурное отношение одна двадцать четвертая), все объекты, расположенные на расстоянии от 20 футов от линзы до бесконечности от нее (например, неподвижная звезда), находятся в одинаково хорошем фокусе. Поэтому двадцать футов называют «фокусным расстоянием» линзы, когда используется эта диафрагма. Фокусное расстояние, следовательно, является расстоянием ближайшего объекта, который будет в хорошем фокусе, когда матовое стекло настроено на чрезвычайно удаленный объект. В одной и той же линзе фокусное расстояние будет зависеть от размера используемой диафрагмы, в то время как в разных линзах с одинаковым апертурным отношением фокусные расстояния будут больше по мере увеличения фокусного расстояния линзы. Термины «апертальное отношение» и «фокусное расстояние» не вошли в общее употребление, но было бы весьма желательно, чтобы они вошли в употребление, чтобы избежать двусмысленности и околичностей при описании свойств фотографических объективов. [21]
В 1874 году Джон Генри Даллмейер назвал это отношение «коэффициентом интенсивности» линзы:
Быстрота линзы зависит от отношения или соотношения апертуры к эквивалентному фокусу. Чтобы выяснить это, разделите эквивалентный фокус на диаметр фактической рабочей апертуры рассматриваемой линзы; и запишите частное как знаменатель с 1, или единицей, для числителя. Таким образом, чтобы найти соотношение линзы диаметром 2 дюйма и фокусом 6 дюймов, разделите фокус на апертуру, или 6, деленное на 2, равно 3; т. е. 1 ⁄ 3 является отношением интенсивности. [22]
Хотя у него еще не было доступа к теории диафрагм и зрачков Эрнста Аббе [23] , которая была широко распространена Зигфридом Чапским в 1893 году [24] , Даллмейер знал, что его рабочая апертура не совпадает с физическим диаметром апертурной диафрагмы:
Однако следует отметить, что для того, чтобы найти реальное отношение интенсивности , необходимо определить диаметр фактической рабочей апертуры. Это легко сделать в случае одиночных линз или для двойных комбинированных линз, используемых с полным отверстием, для этого требуется всего лишь применение циркуля или линейки; но когда используются двойные или тройные комбинированные линзы с диафрагмами, вставленными между комбинациями, это несколько сложнее; поскольку очевидно, что в этом случае диаметр используемой диафрагмы не является мерой фактического пучка света, передаваемого передней комбинацией. Чтобы выяснить это, сфокусируйтесь на удаленном объекте, снимите фокусировочный экран и замените его коллодиевым слайдом, предварительно вставив кусок картона вместо подготовленной пластины. Сделайте небольшое круглое отверстие в центре картона с помощью пирсинга, а затем уберите в затемненную комнату; поставьте свечу близко к отверстию и наблюдайте за освещенным пятном, видимым на передней комбинации; диаметр этого круга, тщательно измеренный, является фактической рабочей апертурой рассматриваемой линзы для конкретной используемой диафрагмы. [22]
Этот момент еще раз подчеркивается Чапским в 1893 году. [24] Согласно английской рецензии на его книгу в 1894 году, «настоятельно подчеркивается необходимость четкого различия между эффективной апертурой и диаметром физической диафрагмы». [25]
Сын Дж. Х. Даллмейера, Томас Рудольфус Даллмейер , изобретатель телеобъектива, в 1899 году перенял терминологию отношения интенсивности . [26]
Системы нумерации апертур

В то же время существовало несколько систем нумерации диафрагмы, разработанных с целью заставить время экспозиции изменяться в прямой или обратной пропорции с диафрагмой, а не с квадратом числа f или обратным квадратом апертурного отношения или отношения интенсивности. Но все эти системы включали некоторую произвольную константу, в отличие от простого отношения фокусного расстояния и диаметра.
Например, Единая система (US) диафрагм была принята в качестве стандарта Фотографическим обществом Великобритании в 1880-х годах. В 1891 году Ботэмли сказал: «Стопы всех лучших производителей теперь расположены в соответствии с этой системой». [27] US 16 — это та же диафрагма, что иж /16, но апертуры, которые больше или меньше на одну целую ступень, используют удвоение или уменьшение вдвое числа США, напримерж /11это США 8 иж /8US 4. Требуемое время экспозиции прямо пропорционально числу US. Eastman Kodak использовала US-стопы на многих своих камерах, по крайней мере, в 1920-х годах.
К 1895 году Ходжес противоречит Ботэмли, утверждая, что система чисел f взяла верх: «Это называетсяж / хсистема, и диафрагмы всех современных объективов хорошей конструкции имеют такую маркировку." [28]
Вот ситуация, как она выглядела в 1899 году:
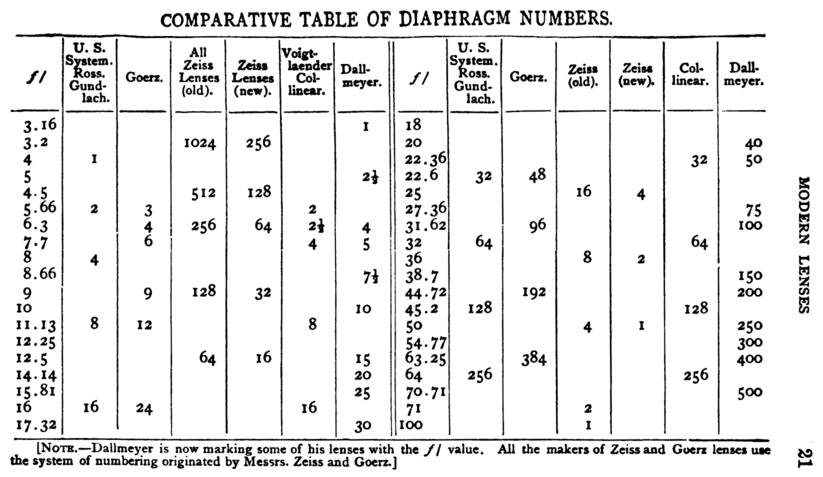
Пайпер в 1901 году [29] обсуждает пять различных систем маркировки диафрагмы: старая и новая системы Цейсса , основанные на фактической интенсивности (пропорциональной обратному квадрату числа f); и системы US, CI и Dallmeyer, основанные на экспозиции (пропорциональной квадрату числа f). Он называет число f «числом отношения», «числом отношения диафрагмы» и «отношением диафрагмы». Он называет выражения типаж /8"дробный диаметр" диафрагмы, хотя он буквально равен "абсолютному диаметру", который он выделяет как другой термин. Он также иногда использует выражения типа "диафрагма f 8" без деления, обозначенного косой чертой.
Бек и Эндрюс в 1902 году говорят о стандарте Королевского фотографического обществаж /4,ж /5.6,ж /8,ж /11.3и т. д. [30] RPS сменила название и вышла из системы США где-то между 1895 и 1902 годами.
Типографская стандартизация


К 1920 году термин f-число появился в книгах как F число и f/число . В современных публикациях формы f-число и f число встречаются чаще, хотя более ранние формы, а также F-число все еще встречаются в нескольких книгах; нередко начальная строчная буква f в f-числе или f/числе набирается в крючковой курсивной форме: ƒ. [31]
Обозначения для f-чисел также были весьма изменчивы в начале двадцатого века. Иногда они писались с заглавной буквы F, [32] иногда с точкой вместо косой черты, [33] а иногда устанавливались в виде вертикальной дроби. [34]
В стандарте ASA 1961 года PH2.12-1961 «Американские стандартные универсальные фотографические экспонометры (фотоэлектрического типа)» указано, что «символом относительной апертуры должно быть ƒ/ или ƒ:, за которым следует эффективное число ƒ». Они показывают изогнутый курсив «ƒ» не только в символе, но и в термине « число f» , которое сегодня чаще всего набирается обычным некурсивным шрифтом.
Смотрите также
- Круг неразберихи
- Группа ф/64
- Конструкция фотографического объектива
- Пинхол-камера
- Предпочтительный номер
Ссылки
- ^ ab Smith, Warren Modern Optical Engineering , 4-е изд., 2007 McGraw-Hill Professional, стр. 183.
- ^ Хехт, Юджин (1987). Оптика (2-е изд.). Эддисон Уэсли. стр. 152. ISBN 0-201-11609-X.
- ^ Грейвенкамп, Джон Э. (2004). Полевое руководство по геометрической оптике . SPIE Field Guides vol. FG01. Беллингхэм, Вашингтон: SPIE . стр. 29. ISBN 9780819452948. OCLC 53896720.
- ^ Смит, Уоррен Современный дизайн линз 2005 McGraw-Hill.
- ^ ISO, Фотография — Диафрагмы и связанные с ними свойства, относящиеся к фотографическим объективам — Обозначения и измерения, ISO 517:2008
- ^ См . Площадь круга .
- ^ Гарри С. Бокс (2003). Справочник техника по освещению на съёмочной площадке: кинооборудование, практика и электрораспределение (3-е изд.). Focal Press. ISBN 978-0-240-80495-8.
- ^ Пол Кей (2003). Подводная фотография. Гильдия мастеров-ремесленников. ISBN 978-1-86108-322-7.
- ^ Дэвид В. Самуэльсон (1998). Руководство для кинематографистов (2-е изд.). Focal Press. ISBN 978-0-240-51480-2.
- ^ Пропускание, пропускание света Архивировано 2021-05-08 на Wayback Machine , DxOMark
- ^ Обзор объектива Sigma 85mm F1.4 Art: новый эталон. Архивировано 04.01.2018 на Wayback Machine , DxOMark
- ^ Цветопередача в биноклях и объективах - Цвета и передача Архивировано 04.01.2018 на Wayback Machine , LensTip.com
- ^ ab "Kodak Motion Picture Camera Films". Eastman Kodak . Ноябрь 2000. Архивировано из оригинала 2002-10-02 . Получено 2007-09-02 .
- ^ "Marianne Oelund, "Lens T-stops", dpreview.com, 2009". Архивировано из оригинала 2012-11-10 . Получено 2013-01-11 .
- ^ Майкл Джон Лэнгфорд (2000). Basic Photography . Focal Press . ISBN 0-240-51592-7.
- ^ Леви, Майкл (2001). Выбор и использование классических камер: руководство пользователя по оценке характеристик, состояния и удобства использования классических камер . Amherst Media, Inc. стр. 163. ISBN 978-1-58428-054-5.
- ^ Хехт, Юджин (1987). Оптика (2-е изд.). Эддисон Уэсли . ISBN 0-201-11609-X.Раздел 5.7.1
- ^ Charles F. Claver; et al. (2007-03-19). "LSST Reference Design" (PDF) . LSST Corporation: 45–50. Архивировано из оригинала (PDF) 2009-03-06 . Получено 2011-01-10 .
{{cite journal}}: Цитировать журнал требует|journal=( помощь ) - ^ Дриггерс, Рональд Г. (2003). Энциклопедия оптической инженерии: Pho-Z, страницы 2049-3050. CRC Press. ISBN 978-0-8247-4252-2. Получено 18.06.2020 .
- ^ аб Грейвенкамп, Джон Э. (2004). Полевое руководство по геометрической оптике . Полевые руководства SPIE, том. ФГ01 . ШПИОН. ISBN 0-8194-5294-7.стр. 29.
- ↑ Томас Саттон и Джордж Доусон, Словарь фотографии , Лондон: Sampson Low, Son & Marston, 1867, (стр. 122).
- ^ Джон Генри Даллмейер, Фотографические объективы: об их выборе и использовании – Специальное издание, отредактированное для американских фотографов , брошюра, 1874 г.
- ^ Саутхолл, Джеймс П.С. (1910). Принципы и методы геометрической оптики: особенно в применении к теории оптических приборов. Macmillan. стр. 537.
- ^ ab Зигфрид Чапский, Theorie der optischen Instrumente, nach Abbe, Бреслау: Trewendt, 1893.
- ↑ Генри Крю, «Теория оптических инструментов доктора Чапского», в «Астрономии и астрофизике» XIII, стр. 241–243, 1894.
- ↑ Томас Р. Даллмейер, Телефотография: Элементарный трактат о конструкции и применении телеобъектива , Лондон: Heinemann, 1899.
- ↑ CH Bothamley, Ilford Manual of Photography , Лондон: Britannia Works Co. Ltd., 1891.
- ↑ Джон А. Ходжес, Фотографические объективы: как выбирать и как использовать , Брэдфорд: Percy Lund & Co., 1895.
- ^ C. Welborne Piper, Первая книга об объективе: Элементарный трактат о действии и использовании фотографического объектива , Лондон: Hazell, Watson, and Viney, Ltd., 1901.
- ↑ Конрад Бек и Герберт Эндрюс, Фотографические объективы: простой трактат , второе издание, Лондон: R. & J. Beck Ltd., ок. 1902 г.
- ^ Поиск Google
- ^ Айвс, Герберт Юджин (1920). Фотография с самолета (Google) . Филадельфия: JB Lippincott. стр. 61. ISBN 9780598722225. Получено 12.03.2007 .
- ^ Мис, Чарльз Эдвард Кеннет (1920). Основы фотографии. Eastman Kodak. стр. 28. Получено 12.03.2007 .
- ^ Дерр, Луис (1906). Фотография для студентов физики и химии (Google) . Лондон: Macmillan. стр. 83. Получено 12.03.2007 .
Внешние ссылки
- Крупноформатная фотография — как выбрать диафрагму




















