Parabolic reflector


A parabolic (or paraboloid or paraboloidal) reflector (or dish or mirror) is a reflective surface used to collect or project energy such as light, sound, or radio waves. Its shape is part of a circular paraboloid, that is, the surface generated by a parabola revolving around its axis. The parabolic reflector transforms an incoming plane wave travelling along the axis into a spherical wave converging toward the focus. Conversely, a spherical wave generated by a point source placed in the focus is reflected into a plane wave propagating as a collimated beam along the axis.
Parabolic reflectors are used to collect energy from a distant source (for example sound waves or incoming star light). Since the principles of reflection are reversible, parabolic reflectors can also be used to collimate radiation from an isotropic source into a parallel beam.[1] In optics, parabolic mirrors are used to gather light in reflecting telescopes and solar furnaces, and project a beam of light in flashlights, searchlights, stage spotlights, and car headlights. In radio, parabolic antennas are used to radiate a narrow beam of radio waves for point-to-point communications in satellite dishes and microwave relay stations, and to locate aircraft, ships, and vehicles in radar sets. In acoustics, parabolic microphones are used to record faraway sounds such as bird calls, in sports reporting, and to eavesdrop on private conversations in espionage and law enforcement.
Theory
Strictly, the three-dimensional shape of the reflector is called a paraboloid. A parabola is the two-dimensional figure. (The distinction is like that between a sphere and a circle.) However, in informal language, the word parabola and its associated adjective parabolic are often used in place of paraboloid and paraboloidal.[2]
If a parabola is positioned in Cartesian coordinates with its vertex at the origin and its axis of symmetry along the y-axis, so the parabola opens upward, its equation is , where is its focal length. (See "Parabola#In a cartesian coordinate system".) Correspondingly, the dimensions of a symmetrical paraboloidal dish are related by the equation: , where is the focal length, is the depth of the dish (measured along the axis of symmetry from the vertex to the plane of the rim), and is the radius of the dish from the center. All units used for the radius, focal point and depth must be the same. If two of these three quantities are known, this equation can be used to calculate the third.
A more complex calculation is needed to find the diameter of the dish measured along its surface. This is sometimes called the "linear diameter", and equals the diameter of a flat, circular sheet of material, usually metal, which is the right size to be cut and bent to make the dish. Two intermediate results are useful in the calculation: (or the equivalent: ) and , where F, D, and R are defined as above. The diameter of the dish, measured along the surface, is then given by: , where means the natural logarithm of x, i.e. its logarithm to base "e".
The volume of the dish is given by where the symbols are defined as above. This can be compared with the formulae for the volumes of a cylinder a hemisphere where and a cone is the aperture area of the dish, the area enclosed by the rim, which is proportional to the amount of sunlight the reflector dish can intercept. The area of the concave surface of the dish can be found using the area formula for a surface of revolution which gives . providing . The fraction of light reflected by the dish, from a light source in the focus, is given by , where and are defined as above.
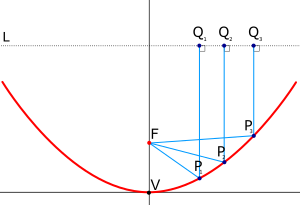
The parabolic reflector functions due to the geometric properties of the paraboloidal shape: any incoming ray that is parallel to the axis of the dish will be reflected to a central point, or "focus". (For a geometrical proof, click here.) Because many types of energy can be reflected in this way, parabolic reflectors can be used to collect and concentrate energy entering the reflector at a particular angle. Similarly, energy radiating from the focus to the dish can be transmitted outward in a beam that is parallel to the axis of the dish.
In contrast with spherical reflectors, which suffer from a spherical aberration that becomes stronger as the ratio of the beam diameter to the focal distance becomes larger, parabolic reflectors can be made to accommodate beams of any width. However, if the incoming beam makes a non-zero angle with the axis (or if the emitting point source is not placed in the focus), parabolic reflectors suffer from an aberration called coma. This is primarily of interest in telescopes because most other applications do not require sharp resolution off the axis of the parabola.
The precision to which a parabolic dish must be made in order to focus energy well depends on the wavelength of the energy. If the dish is wrong by a quarter of a wavelength, then the reflected energy will be wrong by a half wavelength, which means that it will interfere destructively with energy that has been reflected properly from another part of the dish. To prevent this, the dish must be made correctly to within about 1/20 of a wavelength. The wavelength range of visible light is between about 400 and 700 nanometres (nm), so in order to focus all visible light well, a reflector must be correct to within about 20 nm. For comparison, the diameter of a human hair is usually about 50,000 nm, so the required accuracy for a reflector to focus visible light is about 2500 times less than the diameter of a hair. For example, the flaw in the Hubble Space Telescope mirror (too flat by about 2,200 nm at its perimeter) caused severe spherical aberration until corrected with COSTAR.[3]
Microwaves, such as are used for satellite-TV signals, have wavelengths of the order of ten millimetres, so dishes to focus these waves can be wrong by half a millimetre or so and still perform well.
Variations
Focus-balanced reflector

It is sometimes useful if the centre of mass of a reflector dish coincides with its focus. This allows it to be easily turned so it can be aimed at a moving source of light, such as the Sun in the sky, while its focus, where the target is located, is stationary. The dish is rotated around axes that pass through the focus and around which it is balanced. If the dish is symmetrical and made of uniform material of constant thickness, and if F represents the focal length of the paraboloid, this "focus-balanced" condition occurs if the depth of the dish, measured along the axis of the paraboloid from the vertex to the plane of the rim of the dish, is 1.8478 times F. The radius of the rim is 2.7187 F.[a] The angular radius of the rim as seen from the focal point is 72.68 degrees.
Scheffler reflector
The focus-balanced configuration (see above) requires the depth of the reflector dish to be greater than its focal length, so the focus is within the dish. This can lead to the focus being difficult to access. An alternative approach is exemplified by the Scheffler reflector, named after its inventor, Wolfgang Scheffler. This is a paraboloidal mirror which is rotated about axes that pass through its centre of mass, but this does not coincide with the focus, which is outside the dish. If the reflector were a rigid paraboloid, the focus would move as the dish turns. To avoid this, the reflector is flexible, and is bent as it rotates so as to keep the focus stationary. Ideally, the reflector would be exactly paraboloidal at all times. In practice, this cannot be achieved exactly, so the Scheffler reflector is not suitable for purposes that require high accuracy. It is used in applications such as solar cooking, where sunlight has to be focused well enough to strike a cooking pot, but not to an exact point.[4]
Off-axis reflectors

A circular paraboloid is theoretically unlimited in size. Any practical reflector uses just a segment of it. Often, the segment includes the vertex of the paraboloid, where its curvature is greatest, and where the axis of symmetry intersects the paraboloid. However, if the reflector is used to focus incoming energy onto a receiver, the shadow of the receiver falls onto the vertex of the paraboloid, which is part of the reflector, so part of the reflector is wasted. This can be avoided by making the reflector from a segment of the paraboloid which is offset from the vertex and the axis of symmetry. The whole reflector receives energy, which is then focused onto the receiver. This is frequently done, for example, in satellite-TV receiving dishes, and also in some types of astronomical telescope (e.g., the Green Bank Telescope, the James Webb Space Telescope).
Accurate off-axis reflectors, for use in solar furnaces and other non-critical applications, can be made quite simply by using a rotating furnace, in which the container of molten glass is offset from the axis of rotation. To make less accurate ones, suitable as satellite dishes, the shape is designed by a computer, then multiple dishes are stamped out of sheet metal.
Off-axis-reflectors heading from medium latitudes to a geostationary TV satellite somewhere above the equator stand steeper than a coaxial reflector. The effect is, that the arm to hold the dish can be shorter and snow tends less to accumulate in (the lower part of) the dish.

History
The principle of parabolic reflectors has been known since classical antiquity, when the mathematician Diocles described them in his book On Burning Mirrors and proved that they focus a parallel beam to a point.[5] Archimedes in the third century BCE studied paraboloids as part of his study of hydrostatic equilibrium,[6] and it has been claimed that he used reflectors to set the Roman fleet alight during the Siege of Syracuse.[7] This seems unlikely to be true, however, as the claim does not appear in sources before the 2nd century CE, and Diocles does not mention it in his book.[8] Parabolic mirrors and reflectors were also studied extensively by the physicist Roger Bacon in the 13th century AD.[9] James Gregory, in his 1663 book Optica Promota (1663), pointed out that a reflecting telescope with a mirror that was parabolic would correct spherical aberration as well as the chromatic aberration seen in refracting telescopes. The design he came up with bears his name: the "Gregorian telescope"; but according to his own confession, Gregory had no practical skill and he could find no optician capable of actually constructing one.[10] Isaac Newton knew about the properties of parabolic mirrors but chose a spherical shape for his Newtonian telescope mirror to simplify construction.[11] Lighthouses also commonly used parabolic mirrors to collimate a point of light from a lantern into a beam, before being replaced by more efficient Fresnel lenses in the 19th century. In 1888, Heinrich Hertz, a German physicist, constructed the world's first parabolic reflector antenna.[12]
Applications

The most common modern applications of the parabolic reflector are in satellite dishes, reflecting telescopes, radio telescopes, parabolic microphones, solar cookers, and many lighting devices such as spotlights, car headlights, PAR lamps and LED housings.[14]

The Olympic Flame is traditionally lit at Olympia, Greece, using a parabolic reflector concentrating sunlight, and is then transported to the venue of the Games. Parabolic mirrors are one of many shapes for a burning glass.
Parabolic reflectors are popular for use in creating optical illusions. These consist of two opposing parabolic mirrors, with an opening in the center of the top mirror. When an object is placed on the bottom mirror, the mirrors create a real image, which is a virtually identical copy of the original that appears in the opening. The quality of the image is dependent upon the precision of the optics. Some such illusions are manufactured to tolerances of millionths of an inch.
A parabolic reflector pointing upward can be formed by rotating a reflective liquid, like mercury, around a vertical axis. This makes the liquid-mirror telescope possible. The same technique is used in rotating furnaces to make solid reflectors.
Parabolic reflectors are also a popular alternative for increasing wireless signal strength. Even with simple ones, users have reported 3 dB or more gains.[15][16]
See also
- John D. Kraus
- Liquid-mirror telescope, paraboloids produced by rotation
- Parabolic antenna
- Parabolic trough
- Solar furnace
- Toroidal reflector
Footnotes
- ^ The closeness of this number to the value of "e", the base of natural logarithms, is just an accidental coincidence, but it does make a useful mnemonic.
References
- ^ Fitzpatrick, Richard (2007-07-14). "Spherical Mirrors". Farside.ph.utexas.edu. Retrieved 2012-11-08.
- ^ "3D Printing Using a 60 GHz Millimeter Wave Segmented Parabolic Reflective Curved Antenna".
- ^ "Servicing Mission 1". NASA. Archived from the original on April 20, 2008. Retrieved April 26, 2008.
- ^ Administrator. "The Scheffler-Reflector". www.solare-bruecke.org.
- ^ pp. 162–164, Apollonius of Perga's Conica: text, context, subtext, Michael N. Fried and Sabetai Unguru, Brill, 2001, ISBN 90-04-11977-9.
- ^ pp. 73–74, The forgotten revolution: how science was born in 300 BC and why it had to be reborn, Lucio Russo, Birkhäuser, 2004, ISBN 3-540-20068-1.
- ^ "Archimedes' Weapon". Time Magazine. November 26, 1973. Archived from the original on October 12, 2007. Retrieved 2007-08-12.
- ^ p. 72, The Geometry of Burning-Mirrors in Antiquity, Wilbur Knorr, Isis 74 #1 (March 1983), pp. 53–73, doi:10.1086/353176.
- ^ pp. 465, 468, 469, A Pioneer in Anaclastics: Ibn Sahl on Burning Mirrors and Lenses, Roshdi Rashed, Isis, 81, #3 (September 1990), pp. 464–491, doi:10.1086/355456.
- ^ Chambers, Robert (1875). A biographical dictionary of eminent Scotsmen. Oxford University. p. 175.
- ^ McLean, Ian S (2008-07-29). Electronic Imaging in Astronomy: Detectors and Instrumentation. ISBN 9783540765820. Retrieved 2012-11-08.
- ^ "Prehistory of Radio Astronomy". www.nrao.edu.
- ^ "ALMA Doubles its Power in New Phase of More Advanced Observations". ESO Announcement. Retrieved 11 January 2013.
- ^ Fitzpatrick, Richard (2007-07-14). "Spherical Mirrors". Farside.ph.utexas.edu. Retrieved 2012-11-08.
- ^ "Parabolic Reflector Free WiFi Booster". Do-It-Yourself Wireless Antennas Update and Wi-Fi Resource Center | WiFi Wireless Q & A. Binarywolf.com. 2009-08-26. Archived from the original on 2019-06-09. Retrieved 2012-11-08.
- ^ "Slideshow: Wi-Fi Shootout in the Desert". Wired. 2004-08-03. Retrieved 2012-11-08.
External links
- Java demonstration of a parabolic reflector
- Parabolic Reflector Antennas www.antenna-theory.com
- Animations demonstrating parabola mirror by QED
- Make Big Paraboloid Reflectors Using Plane Segments























