метрика Керра
| Общая теория относительности |
|---|
 |
Метрика Керра или геометрия Керра описывает геометрию пустого пространства-времени вокруг вращающейся незаряженной аксиально-симметричной черной дыры с квазисферическим горизонтом событий . Метрика Керра является точным решением уравнений поля Эйнштейна общей теории относительности ; эти уравнения являются сильно нелинейными , что делает поиск точных решений очень сложным.
Обзор
Метрика Керра является обобщением на вращающееся тело метрики Шварцшильда, открытой Карлом Шварцшильдом в 1915 году, которая описывала геометрию пространства-времени вокруг незаряженного, сферически симметричного и невращающегося тела. Соответствующее решение для заряженного , сферического, невращающегося тела, метрика Рейсснера–Нордстрема , было открыто вскоре после этого (1916–1918). Однако точное решение для незаряженной вращающейся черной дыры, метрика Керра, оставалось нерешенным до 1963 года, когда ее открыл Рой Керр . [1] [2] : 69–81 Естественное расширение на заряженную вращающуюся черную дыру, метрика Керра–Ньюмена , было открыто вскоре после этого в 1965 году. Эти четыре связанных решения можно суммировать в следующей таблице, где Q представляет электрический заряд тела , а J представляет его спиновый угловой момент :
Не вращающийся ( J = 0) Вращение ( J ∈ ) Незаряженный ( Q = 0) Шварцшильд Керр Заряжено ( Q ∈ ) Рейсснер–Нордстрём Керр–Ньюман
Согласно метрике Керра, вращающееся тело должно демонстрировать эффект увлечения системы отсчета (также известный как прецессия Лензе–Тирринга ), отличительное предсказание общей теории относительности. Первое измерение этого эффекта увлечения системы отсчета было выполнено в 2011 году экспериментом Gravity Probe B. Грубо говоря, этот эффект предсказывает, что объекты, приближающиеся к вращающейся массе, будут вовлечены в ее вращение не из-за какой-либо приложенной силы или крутящего момента, которые можно почувствовать, а скорее из-за закрученной кривизны самого пространства-времени, связанной с вращающимися телами. В случае вращающейся черной дыры на достаточно близких расстояниях все объекты — даже свет — должны вращаться вместе с черной дырой; область, где это имеет место, называется эргосферой .
Свет от удаленных источников может несколько раз обойти горизонт событий (если они достаточно близко), создавая множественные изображения одного и того же объекта . Для удаленного наблюдателя кажущееся перпендикулярное расстояние между изображениями уменьшается в e 2 π раз (около 500). Однако быстро вращающиеся черные дыры имеют меньшее расстояние между множественными изображениями. [3] [4]
Вращающиеся черные дыры имеют поверхности, где метрика, по-видимому, имеет очевидные сингулярности ; размер и форма этих поверхностей зависят от массы и углового момента черной дыры. Внешняя поверхность охватывает эргосферу и имеет форму, похожую на сплющенную сферу. Внутренняя поверхность отмечает горизонт событий; объекты, проходящие внутрь этого горизонта, никогда больше не смогут общаться с миром за его пределами. Однако ни одна из поверхностей не является истинной сингулярностью, поскольку их кажущаяся сингулярность может быть устранена в другой системе координат . Похожая ситуация возникает при рассмотрении метрики Шварцшильда, которая также, по-видимому, приводит к сингулярности в точке , разделяющей пространство выше и ниже r s на два несвязанных участка; используя другое преобразование координат, можно затем связать расширенный внешний участок с внутренним участком (см. Метрика Шварцшильда § Сингулярности и черные дыры ) — такое преобразование координат устраняет кажущуюся сингулярность там, где встречаются внутренняя и внешняя поверхности. Объекты между этими двумя поверхностями должны вращаться совместно с вращающейся черной дырой, как отмечено выше; Эту особенность в принципе можно использовать для извлечения энергии из вращающейся черной дыры вплоть до ее инвариантной массовой энергии Mc 2 .
Эксперимент LIGO, впервые обнаруживший гравитационные волны и анонсированный в 2016 году, также обеспечил первое прямое наблюдение пары черных дыр Керра. [5]
Метрический
Метрика Керра обычно выражается в одной из двух форм: форма Бойера–Линдквиста и форма Керра–Шилда. Она может быть легко выведена из метрики Шварцшильда, используя алгоритм Ньюмена–Джаниса [6] с помощью формализма Ньюмена–Пенроуза (также известного как формализм спин-коэффициента), [7] уравнения Эрнста , [8] или преобразования координат эллипсоида. [9]
Координаты Бойера–Линдквиста
Метрика Керра описывает геометрию пространства-времени вблизи массы , вращающейся с угловым моментом . [10] Метрика (или, что эквивалентно, ее линейный элемент для собственного времени ) в координатах Бойера–Линдквиста равна [11] [12]
| 1 |
где координаты являются стандартными сплюснутыми сфероидальными координатами , которые эквивалентны декартовым координатам [13] [14]
| 2 |
| 3 |
| 4 |
где радиус Шварцшильда
| 5 |
и где для краткости шкалы длины и были введены как
| 6 |
| 7 |
| 8 |
Ключевой особенностью, которую следует отметить в приведенной выше метрике, является перекрестный член . Это подразумевает, что существует связь между временем и движением в плоскости вращения, которая исчезает, когда угловой момент черной дыры стремится к нулю.
В нерелятивистском пределе, где (или, что эквивалентно, ) стремится к нулю, метрика Керра становится ортогональной метрикой для сплюснутых сфероидальных координат
| 9 |
Координаты Керра–Шилда
Метрику Керра можно выразить в форме «Керра–Шилда» , используя определенный набор декартовых координат следующим образом. [15] [16] [17] Эти решения были предложены Керром и Шильдом в 1965 году.
| 10 |
| 11 |
| 12 |
| 13 |
Обратите внимание, что k — единичный 3-вектор , что делает 4-вектор нулевым вектором по отношению как к g , так и к η . [18] Здесь M — постоянная масса вращающегося объекта, η — тензор Минковского , а a — постоянный параметр вращения вращающегося объекта. Подразумевается, что вектор направлен вдоль положительной оси z. Величина r не является радиусом, а скорее неявно определяется как
| 14 |
Обратите внимание, что величина r становится обычным радиусом R
когда параметр вращения приближается к нулю. В этой форме решения единицы выбираются так, чтобы скорость света была равна единице ( ). На больших расстояниях от источника ( R ≫ a ) эти уравнения сводятся к форме Эддингтона–Финкельштейна метрики Шварцшильда.
В форме Керра–Шилда метрики Керра определитель метрического тензора везде равен отрицательной единице, даже вблизи источника. [19]
Координаты солитона
Поскольку метрика Керра (вместе с метрикой Керра–NUT) является аксиально-симметричной, ее можно привести к форме, к которой можно применить преобразование Белинского–Захарова . Это подразумевает, что черная дыра Керра имеет форму гравитационного солитона . [20]
Масса вращательной энергии
Если извлечь полную вращательную энергию черной дыры, например, с помощью процесса Пенроуза , [21] [22] оставшаяся масса не может уменьшиться ниже неприводимой массы. Следовательно, если черная дыра вращается со спином , ее полный эквивалент массы выше в раз по сравнению с соответствующей черной дырой Шварцшильда, где равно . Причина этого в том, что для того, чтобы заставить статическое тело вращаться, к системе необходимо приложить энергию. Из-за эквивалентности массы и энергии эта энергия также имеет эквивалент массы, который добавляется к полной массе и энергии системы, .
Полный эквивалент массы (гравитационная масса) тела (включая его энергию вращения ) и его неприводимая масса связаны соотношением [23] [24]
Волновой оператор
Поскольку даже прямая проверка метрики Керра требует громоздких вычислений, контравариантные компоненты метрического тензора в координатах Бойера–Линдквиста показаны ниже в выражении для квадрата оператора четырехградиента : [21]
| 15 |
Перетаскивание кадра
Мы можем переписать метрику Керра ( 1 ) в следующем виде:
| 16 |
Эта метрика эквивалентна совращающейся системе отсчета, которая вращается с угловой скоростью Ω, зависящей как от радиуса r, так и от кошироты θ , где Ω называется горизонтом Киллинга .
| 17 |
Таким образом, инерциальная система отсчета увлекается вращающейся центральной массой, чтобы участвовать во вращении последней; это называется увлечением системы отсчета и было проверено экспериментально. [25] Качественно увлечение системой отсчета можно рассматривать как гравитационный аналог электромагнитной индукции. «Конькобежец», находящийся на орбите над экватором и вращательно покоящийся относительно звезд, вытягивает свои руки. Рука, вытянутая к черной дыре, будет закручена в направлении вращения. Рука, вытянутая от черной дыры, будет закручена в направлении анти-вращения. Поэтому она будет вращательно ускорена в направлении, противоположном вращению черной дыры. Это противоположно тому, что происходит в повседневном опыте. Если она уже вращается с определенной скоростью, когда вытягивает свои руки, инерционные эффекты и эффекты увлечения системой отсчета будут сбалансированы, и ее вращение не изменится. Из-за принципа эквивалентности гравитационные эффекты локально неотличимы от инерционных эффектов, поэтому эта скорость вращения, при которой, когда она вытягивает руки, ничего не происходит, является ее локальной точкой отсчета для отсутствия вращения. Эта система вращается относительно неподвижных звезд и вращается в противоположном направлении относительно черной дыры. Полезной метафорой является планетарная зубчатая система, в которой черная дыра является солнечной шестерней, фигурист — планетарной шестерней, а внешняя вселенная — кольцевой шестерней. Это также можно интерпретировать с помощью принципа Маха .
Важные поверхности

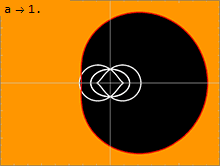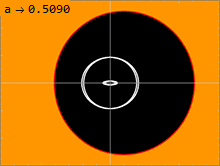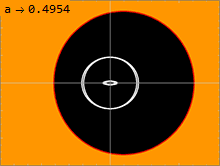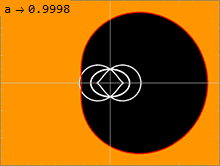
В метрике Керра ( 1 ) есть несколько важных поверхностей . Внутренняя поверхность соответствует горизонту событий, подобному наблюдаемому в метрике Шварцшильда; это происходит там, где чисто радиальная компонента g rr метрики стремится к бесконечности. Решение квадратного уравнения 1/г рр = 0 дает решение:
что в натуральных единицах (которые дают ) упрощается до:
В то время как в метрике Шварцшильда горизонт событий также является местом, где чисто временная компонента метрики g tt меняет знак с положительного на отрицательный, в метрике Керра это происходит на другом расстоянии. Снова решая квадратное уравнение g tt = 0 , получаем решение:
или в натуральных единицах:
Из-за члена cos 2 θ в квадратном корне эта внешняя поверхность напоминает сплющенную сферу, которая касается внутренней поверхности на полюсах оси вращения, где коширота θ равна 0 или π ; пространство между этими двумя поверхностями называется эргосферой. Внутри этого объема чисто временной компонент g tt отрицателен, т. е. действует как чисто пространственный метрический компонент. Следовательно, частицы внутри этой эргосферы должны вращаться совместно с внутренней массой, если они хотят сохранить свой временной характер. Движущаяся частица испытывает положительное собственное время вдоль своей мировой линии , своего пути через пространство-время. Однако это невозможно внутри эргосферы, где g tt отрицателен, если только частица не вращается совместно вокруг внутренней массы с угловой скоростью не менее . Таким образом, ни одна частица не может двигаться в направлении, противоположном вращению центральной массы внутри эргосферы.
Как и в случае с горизонтом событий в метрике Шварцшильда, кажущаяся сингулярность в точке r H обусловлена выбором координат (т. е. это координатная сингулярность ). Фактически, пространство-время может быть гладко продолжено через нее с помощью соответствующего выбора координат. В свою очередь, внешняя граница эргосферы в точке r E сама по себе не является сингулярной даже в координатах Керра из-за ненулевого члена .
Эргосфера и процесс Пенроуза
Черная дыра в общем окружена поверхностью, называемой горизонтом событий и расположенной на радиусе Шварцшильда для невращающейся черной дыры, где скорость убегания равна скорости света. Внутри этой поверхности ни один наблюдатель/частица не может поддерживать себя на постоянном радиусе. Она вынуждена падать внутрь, и поэтому это иногда называют статическим пределом .
Вращающаяся черная дыра имеет тот же статический предел на своем горизонте событий, но за пределами горизонта событий имеется дополнительная поверхность, называемая «эргоповерхностью», определяемая формулой
в координатах Бойера–Линдквиста , которые можно интуитивно охарактеризовать как сферу, где «скорость вращения окружающего пространства» увлекается вместе со скоростью света. Внутри этой сферы увлечение больше скорости света, и любой наблюдатель/частица вынужден вращаться вместе с ней.
Область за пределами горизонта событий, но внутри поверхности, где скорость вращения равна скорости света, называется эргосферой ( от греческого ergon — работа ). Частицы, падающие в эргосферу, вынуждены вращаться быстрее и тем самым получать энергию. Поскольку они все еще находятся за пределами горизонта событий, они могут покинуть черную дыру. Чистый процесс заключается в том, что вращающаяся черная дыра испускает энергичные частицы за счет своей собственной полной энергии. Возможность извлечения энергии спина из вращающейся черной дыры была впервые предложена математиком Роджером Пенроузом в 1969 году и поэтому называется процессом Пенроуза. Вращающиеся черные дыры в астрофизике являются потенциальным источником большого количества энергии и используются для объяснения энергетических явлений, таких как гамма-всплески .
Функции
Геометрия Керра демонстрирует множество примечательных особенностей: максимальное аналитическое расширение включает последовательность асимптотически плоских внешних областей, каждая из которых связана с эргосферой , стационарными предельными поверхностями, горизонтами событий , горизонтами Коши , замкнутыми времениподобными кривыми и сингулярностью кривизны в форме кольца . Геодезическое уравнение может быть решено точно в замкнутой форме. В дополнение к двум векторным полям Киллинга (соответствующим переносу времени и осесимметрии ), геометрия Керра допускает замечательный тензор Киллинга . Существует пара главных нулевых конгруэнций (одна входящая и одна исходящая ). Тензор Вейля является алгебраически специальным , фактически он имеет тип Петрова D. Глобальная структура известна. Топологически гомотопический тип пространства-времени Керра можно просто охарактеризовать как линию с окружностями, прикрепленными в каждой целочисленной точке.
Обратите внимание, что внутренняя геометрия Керра нестабильна по отношению к возмущениям во внутренней области. Эта нестабильность означает, что хотя метрика Керра является осесимметричной, черная дыра, созданная посредством гравитационного коллапса, может быть не таковой. [13] Эта нестабильность также подразумевает, что многие из особенностей геометрии Керра, описанных выше, могут отсутствовать внутри такой черной дыры. [27] [28]
Поверхность, по которой свет может вращаться вокруг черной дыры, называется фотонной сферой. Решение Керра имеет бесконечно много фотонных сфер , лежащих между внутренней и внешней. В невращающемся решении Шварцшильда с внутренняя и внешняя фотонные сферы вырождаются, так что на одном радиусе находится только одна фотонная сфера. Чем больше спин черной дыры, тем дальше друг от друга движутся внутренняя и внешняя фотонные сферы. Луч света, движущийся в направлении, противоположном спину черной дыры, будет вращаться по круговой орбите вокруг дыры во внешней фотонной сфере. Луч света, движущийся в том же направлении, что и спин черной дыры, будет вращаться по круговой орбите во внутренней фотонной сфере. Орбитальные геодезические с некоторым угловым моментом, перпендикулярным оси вращения черной дыры, будут вращаться по фотонным сферам между этими двумя крайностями. Поскольку пространство-время вращается, такие орбиты демонстрируют прецессию , поскольку происходит сдвиг переменной после завершения одного периода переменной .
Уравнения траектории


Уравнения движения для тестовых частиц в пространстве-времени Керра управляются четырьмя константами движения . [29] Первая — это инвариантная масса тестового тела, определяемая соотношением, где — это 4-импульс частицы. Кроме того, существуют две константы движения, заданные симметриями временного переноса и вращения пространства-времени Керра, энергия и компонент орбитального углового момента, параллельный спину черной дыры . [21] [30] и
Используя теорию Гамильтона-Якоби , Брэндон Картер показал, что существует четвертая константа движения, , [29] теперь называемая константой Картера . Она связана с полным угловым моментом частицы и определяется как
Поскольку существует четыре (независимых) константы движения для степеней свободы, уравнения движения пробной частицы в пространстве-времени Керра являются интегрируемыми .
Используя эти константы движения, можно записать уравнения траектории для пробной частицы (используя естественные единицы измерения ), [29] с
где — аффинный параметр, такой что . В частности, когда аффинный параметр , связан с собственным временем через .
Из-за эффекта увлечения рамки наблюдатель с нулевым угловым моментом (ZAMO) вращается с угловой скоростью , которая определяется относительно координатного времени бухгалтера . [31] Локальная скорость тестовой частицы измеряется относительно зонда, вращающегося с . Гравитационное замедление времени между ZAMO в фиксированном положении и неподвижным наблюдателем, удаленным от массы , равно В декартовых координатах Керра–Шилда уравнения для фотона имеют вид [32] где аналогично постоянной Картера, а — полезная величина
Если мы установим , геодезические Шварцшильда будут восстановлены.
Симметрии
Группа изометрий метрики Керра является подгруппой десятимерной группы Пуанкаре , которая принимает двумерное место сингулярности в себя. Она сохраняет временные трансляции (одно измерение) и вращения вокруг своей оси вращения (одно измерение). Таким образом, она имеет два измерения. Как и группа Пуанкаре, она имеет четыре связных компонента: компонент тождества; компонент, который обращает время и долготу; компонент, который отражает через экваториальную плоскость; и компонент, который делает и то, и другое.
В физике симметрии обычно связаны с сохраняющимися константами движения в соответствии с теоремой Нётер . Как показано выше, геодезические уравнения имеют четыре сохраняющиеся величины: одна из которых вытекает из определения геодезической, а две из них возникают из временной трансляции и вращательной симметрии геометрии Керра. Четвертая сохраняющаяся величина не возникает из симметрии в стандартном смысле и обычно называется скрытой симметрией.
Сверхэкстремальные решения Kerr
Местоположение горизонта событий определяется большим корнем . Когда (т.е. ), нет (действительных) решений этого уравнения, и нет горизонта событий. Без горизонтов событий, которые могли бы скрыть его от остальной части Вселенной, черная дыра перестает быть черной дырой и вместо этого становится голой сингулярностью . [33]
Черные дыры Керра как червоточины
This section needs additional citations for verification. (February 2011) |
Хотя решение Керра кажется сингулярным в корнях , на самом деле это координатные сингулярности, и при соответствующем выборе новых координат решение Керра может быть плавно продолжено через значения , соответствующие этим корням. Больший из этих корней определяет местоположение горизонта событий, а меньший определяет местоположение горизонта Коши . (Направленная в будущее, подобная времени) кривая может начинаться во внешней области и проходить через горизонт событий. После прохождения через горизонт событий координата теперь ведет себя как временная координата, поэтому она должна уменьшаться до тех пор, пока кривая не пройдет через горизонт Коши. [34]
Анти-вселенная область
Метрика Керра, описывающая геометрию пространства-времени вокруг вращающейся черной дыры, может быть расширена за пределы внутреннего горизонта событий. В системе координат Бойера-Линдквиста этот внутренний горизонт расположен в
По мере пересечения этого внутреннего горизонта радиальная координата продолжает уменьшаться, даже становясь отрицательной.
Кольцевая сингулярность и не только
При возникает своеобразная особенность: кольцевая сингулярность. В отличие от точечной сингулярности в метрике Шварцшильда (невращающейся черной дыры), сингулярность Керра представляет собой не отдельную точку, а кольцо, лежащее в экваториальной плоскости ( ). Эта кольцевая сингулярность действует как портал в новую область пространства-времени.
Если мы избежим экваториальной плоскости ( ), мы можем плавно продолжить координату до отрицательных значений. Эта область с интерпретируется как совершенно новая, асимптотически плоская вселенная, часто называемая «антивселенной». Эта антивселенная обладает некоторыми удивительными свойствами:
Отрицательная масса ADM: Антивселенная обладает отрицательной массой Арновитта-Дезера-Мизнера (ADM) , которую можно рассматривать как полную массу-энергию пространства-времени, измеренную на бесконечности. Отрицательная масса — это весьма необычное понятие в общей теории относительности, и ее физическая интерпретация все еще обсуждается.
Замкнутые времениподобные кривые и горизонт Коши
В антивселенной происходит еще более странное явление. Метрическая компонента , которая связана с азимутальным направлением вокруг сингулярности кольца, может менять знак. В частности, задается как:
Когда становится отрицательным, координата становится времениподобной, а линейная комбинация координат и становится пространственноподобной. Это приводит к существованию замкнутых времениподобных кривых (ЗВК). ЗВК — это путь через пространство-время, по которому объект может вернуться в свое прошлое, нарушая причинность.
Граница, где впервые появляются изменения знака и КТК, называется горизонтом Коши . Она определяется условием , которое дает
Горизонт Коши действует как граница, за пределами которой привычные понятия причины и следствия рушатся. Наличие ЗВК поднимает фундаментальные вопросы о предсказуемости и последовательности законов физики в этих экстремальных областях пространства-времени.
Область антивселенной расширенной метрики Керра — это увлекательная и озадачивающая теоретическая конструкция. Она представляет собой сценарий с отрицательной массой, обратной ориентацией времени и возможностью путешествия во времени через замкнутые времениподобные кривые. [27] [28] Хотя физическая реальность антивселенной остается неопределенной, ее изучение дает ценные сведения о природе пространства-времени, гравитации и пределах нашего текущего понимания вселенной.
Хотя ожидается, что внешняя область решения Керра стабильна и что все вращающиеся черные дыры в конечном итоге приблизятся к метрике Керра, внутренняя область решения, по-видимому, нестабильна, подобно карандашу, сбалансированному на своем острие. [35] [13] Это связано с идеей космической цензуры .
Связь с другими точными решениями
Геометрия Керра является частным примером стационарного аксиально-симметричного вакуумного решения уравнения поля Эйнштейна . Семейство всех стационарных аксиально-симметричных вакуумных решений уравнения поля Эйнштейна — это вакуумы Эрнста.
Решение Керра также связано с различными невакуумными решениями, которые моделируют черные дыры. Например, электровакуум Керра–Ньюмена моделирует (вращающуюся) черную дыру, наделенную электрическим зарядом, в то время как нулевая пыль Керра–Вайдьи моделирует (вращающуюся) дыру с падающим электромагнитным излучением.
Частный случай метрики Керра дает метрику Шварцшильда, которая моделирует невращающуюся черную дыру, которая является статической и сферически симметричной , в координатах Шварцшильда . (В этом случае каждый момент Героха, кроме массы, обращается в нуль.)
Внутренняя часть геометрии Керра, или, скорее, ее часть, локально изометрична вакууму Чандрасекара–Феррари CPW, примеру модели сталкивающихся плоских волн. Это особенно интересно, поскольку глобальная структура этого решения CPW существенно отличается от структуры геометрии Керра, и в принципе экспериментатор мог бы надеяться изучить геометрию (внешней части) внутренней части Керра, организовав столкновение двух подходящих гравитационных плоских волн .
Мультипольные моменты
Каждый асимптотически плоский вакуум Эрнста можно охарактеризовать, задав бесконечную последовательность релятивистских мультипольных моментов , первые два из которых можно интерпретировать как массу и угловой момент источника поля. Существуют альтернативные формулировки релятивистских мультипольных моментов, предложенные Хансеном, Торном и Герохом, которые, как оказалось, согласуются друг с другом. Релятивистские мультипольные моменты геометрии Керра были вычислены Хансеном; они оказались
Таким образом, частный случай вакуума Шварцшильда ( ) дает «монопольный точечный источник » общей теории относительности. [a]
Мультипольные моменты Вейля возникают при обработке определенной метрической функции (формально соответствующей ньютоновскому гравитационному потенциалу), которая появляется как карта Вейля–Папапетру для семейства Эрнста всех стационарных осесимметричных вакуумных решений с использованием стандартных евклидовых скалярных мультипольных моментов . Они отличаются от моментов, вычисленных Хансеном выше. В некотором смысле моменты Вейля только (косвенно) характеризуют «распределение масс» изолированного источника, и они оказываются зависящими только от релятивистских моментов четного порядка . В случае решений, симметричных относительно экваториальной плоскости, моменты Вейля нечетного порядка исчезают. Для вакуумных решений Керра первые несколько моментов Вейля задаются как
В частности, мы видим, что вакуум Шварцшильда имеет ненулевой момент Вейля второго порядка, что соответствует тому факту, что «монополь Вейля» является вакуумным решением Шази–Керзона, а не вакуумным решением Шварцшильда, которое возникает из ньютоновского потенциала некоторого тонкого стержня конечной длины с однородной плотностью .
В общей теории относительности слабого поля удобно рассматривать изолированные источники, используя другой тип мультиполей, которые обобщают моменты Вейля до массовых мультипольных моментов и импульсных мультипольных моментов , характеризующих соответственно распределение массы и импульса источника. Это многоиндексные величины, чьи соответствующим образом симметризованные и антисимметризованные части могут быть связаны с действительными и мнимыми частями релятивистских моментов для полной нелинейной теории довольно сложным образом.
Перес и Морески дали альтернативное понятие «монопольных решений», расширив стандартную тетраду NP вакуумов Эрнста по степеням (радиальная координата в диаграмме Вейля–Папапетру). Согласно этой формулировке:
- изолированный источник массового монополя с нулевым угловым моментом — это вакуумное семейство Шварцшильда (один параметр),
- изолированный источник массового монополя с радиальным угловым моментом — это вакуумное семейство Тауба–НУТ (два параметра; не совсем асимптотически плоское),
- источник изолированного массового монополя с аксиальным угловым моментом — это вакуумное семейство Керра (два параметра).
В этом смысле вакуумы Керра являются простейшими стационарными осесимметричными асимптотически плоскими вакуумными решениями в общей теории относительности.
Открытые проблемы
Геометрия Керра часто используется в качестве модели вращающейся черной дыры , но если решение считается справедливым только за пределами некоторой компактной области (с учетом определенных ограничений), в принципе, его можно использовать в качестве внешнего решения для моделирования гравитационного поля вокруг вращающегося массивного объекта, отличного от черной дыры, такого как нейтронная звезда или Земля. Это очень хорошо работает для невращающегося случая, когда внешняя часть вакуума Шварцшильда может быть сопоставлена с внутренней частью жидкости Шварцшильда и, конечно, с более общими статическими сферически симметричными решениями идеальной жидкости. Однако проблема нахождения внутренней части вращающейся идеальной жидкости, которая может быть сопоставлена с внешней частью Керра или, конечно, с любым асимптотически плоским решением внешней вакуумной среды, оказалась очень сложной. В частности, жидкость Вальквиста , которая когда-то считалась кандидатом на сопоставление с внешней частью Керра, теперь, как известно, не допускает никакого такого сопоставления. В настоящее время, по-видимому, известны только приближенные решения, моделирующие медленно вращающиеся жидкие шары (это релятивистский аналог сплющенных сфероидальных шаров с ненулевой массой и угловым моментом, но исчезающими высшими мультипольными моментами). Однако внешняя часть диска Нейгебауэра–Мейнела, точное пылевое решение , моделирующее вращающийся тонкий диск, в предельном случае приближается к геометрии Керра . Известны также физические решения для тонкого диска, полученные путем идентификации частей пространства-времени Керра. [36]
Смотрите также
- метрика Шварцшильда
- Метрика Керра–Ньюмана
- Метрика Керра–Ньюмана–де–Ситтера
- Метрика Рейсснера–Нордстрема
- Метрика Хартла–Торна
- Спин-флип
- Вращающаяся черная дыра
Сноски
- ^ Предупреждение: не путайте релятивистские мультипольные моменты, вычисленные Хансеном, с мультипольными моментами Вейля, обсуждаемыми ниже.
Ссылки
- ^ Керр, Рой П. (1963). «Гравитационное поле вращающейся массы как пример алгебраически специальных метрик». Physical Review Letters . 11 (5): 237– 238. Bibcode : 1963PhRvL..11..237K. doi : 10.1103/PhysRevLett.11.237.
- ^ Мелиа, Фульвио (2009). «Взлом кода Эйнштейна: теория относительности и рождение физики черных дыр, с послесловием Роя Керра», Princeton University Press, Принстон, ISBN 978-0226519517
- ^ Снеппен, Альберт (декабрь 2021 г.). «Расходящиеся отражения вокруг фотонной сферы черной дыры». Scientific Reports . 11 (1). Cosmic Dawn Center : 14247. Bibcode :2021NatSR..1114247S. doi :10.1038/s41598-021-93595-w. PMC 8270963 . PMID 34244573.
- ^ Саттер, Пол (22 июля 2021 г.). «Черные дыры деформируют вселенную, превращая ее в гротескный зал зеркал». livescience.com .
- ^ Эббот, Б. П. (11 февраля 2016 г.). «Наблюдение гравитационных волн от слияния бинарных черных дыр». Physical Review Letters . 116 (6): 061102. arXiv : 1602.03837 . Bibcode : 2016PhRvL.116f1102A. doi : 10.1103/PhysRevLett.116.061102. PMID 26918975. S2CID 124959784.
- ^ Ньюман, ET; Дженис, AI (1965-06-01). «Заметка о метрике вращающихся частиц Керра». Журнал математической физики . 6 (6): 915–917 . Bibcode : 1965JMP.....6..915N. doi : 10.1063/1.1704350. ISSN 0022-2488.
- ^ Ньюман, Эзра; Адамо, Тим (2014). «Метрика Керра–Ньюмана». Scholarpedia . 9 (10): 31791. arXiv : 1410.6626 . Bibcode : 2014SchpJ...931791N. doi : 10.4249/scholarpedia.31791 . ISSN 1941-6016.
- ^ Харрисон, Б. Кент (1978-10-30). «Преобразование Бэклунда для уравнения Эрнста общей теории относительности». Physical Review Letters . 41 (18): 1197– 1200. Bibcode : 1978PhRvL..41.1197H. doi : 10.1103/PhysRevLett.41.1197. ISSN 0031-9007.
- ^ Chou, Yu-Ching (январь 2020 г.). «Излучающая черная дыра Керра и излучение Хокинга». Heliyon . 6 (1): e03336. Bibcode :2020Heliy...603336C. doi : 10.1016/j.heliyon.2020.e03336 . PMC 7002888 . PMID 32051884.
- ^ Ландау, Л. Д .; Лифшиц, Э. М. (1975). Классическая теория полей . Курс теоретической физики. Т. 2 (пересмотренное 4-е англ. изд.). Нью-Йорк: Pergamon Press. С. 321–330 . ISBN 978-0-08-018176-9.
- ^ Реццолла, Лучано; Занотти, Олиндо (2013). Релятивистская гидродинамика. Oxford University Press. стр. 55–57 [уравнения 1.249–1.265]. ISBN 978-0-19-852890-6.
- ^ Кристофер М. Хирата: Лекция XXVI: Керровские черные дыры: I. Метрическая структура и регулярность орбит частиц, стр. 1, Ур. 1
- ^ abcd Виссер, Мэтт (2007). «Пространство-время Керра: краткое введение». стр. 15, уравнения 60–61, стр. 24, стр. 35. arXiv : 0706.0622v3 [gr-qc].
- ^ Бойер, Роберт Х.; Линдквист, Ричард В. (1967). «Максимальное аналитическое расширение метрики Керра». J. Math. Phys . 8 (2): 265– 281. Bibcode :1967JMP.....8..265B. doi :10.1063/1.1705193.
- ^ Дебни, GC; Керр, RP; Шильд, A. (1969). «Решения уравнений Эйнштейна и Эйнштейна-Максвелла». Журнал математической физики . 10 (10): 1842– 1854. Bibcode : 1969JMP....10.1842D. doi : 10.1063/1.1664769.Особенно см. уравнения (7.10), (7.11) и (7.14).
- ^ Баласин, Герберт; Нахбагауэр, Герберт (1994). «Распределительный тензор энергии-импульса семейства пространства-времени Керра–Ньюмена». Классическая и квантовая гравитация . 11 (6): 1453– 1461. arXiv : gr-qc/9312028 . Bibcode : 1994CQGra..11.1453B. doi : 10.1088/0264-9381/11/6/010. S2CID 6041750.
- ^ Берман, Марсело. «Энергия черных дыр и Вселенная Хокинга» в книге «Тенденции в исследовании черных дыр» , стр. 148 (ред. Крейтлера, Nova Publishers 2006).
- ^ Виссер, Мэтт (14 января 2008 г.). «Пространство-время Керра: краткое введение». стр. 12. arXiv : 0706.0622 [gr-qc].
- ^ Стефани, Ганс и др. Точные решения уравнений поля Эйнштейна (Cambridge University Press 2003). См. стр. 485 относительно определителя метрического тензора. См. стр. 325 относительно обобщений.
- ^ Белинский, В.; Вердагер, Э. (2001). Гравитационные солитоны . Кембриджские монографии по математической физике. Издательство Кембриджского университета . ISBN 978-0521805865.PDF
- ^ abc Misner, Thorne & Wheeler: Gravitation Архивировано 22 августа 2017 г. в Wayback Machine , страницы 899, 900, 908
- ^ Бхат, Манджири; Дхурандхар, Санджив; Дадхич, Нареш (1985). «Энергетика черной дыры Керра–Ньюмена с помощью процесса Пенроуза». Журнал астрофизики и астрономии . 6 (2): 85– 100. Bibcode : 1985JApA....6...85B. CiteSeerX 10.1.1.512.1400 . doi : 10.1007/BF02715080. S2CID 53513572.
- ^ Тибо Дамур : Черные дыры: Энергетика и термодинамика, стр. 11
- ^ Стейн ван Тонгерен: Вращающиеся черные дыры, страница 42
- ^ Уилл, Клиффорд М. (май 2011 г.). «Наконец-то результаты Gravity Probe B». Physics . 4 : 43. arXiv : 1106.1198 . Bibcode :2011PhyOJ...4...43W. doi :10.1103/Physics.4.43. S2CID 119237335.
- ^ де Врис, Андреас. «Тени вращающихся черных дыр» (PDF) . стр. 8.
- ^ ab Пол Дэвис : О времени: Незаконченная революция Эйнштейна
- ^ ab Научное сотрудничество LIGO; Сотрудничество Virgo (2007). "Пространство-время Керра: краткое введение". стр. 13, ниже уравнение 52. arXiv : 0706.0622v3 [gr-qc].
- ^ abc Carter, Brandon (1968). "Глобальная структура семейства гравитационных полей Керра" (PDF) . Physical Review . 174 (5): 1559– 1571. Bibcode :1968PhRv..174.1559C. doi :10.1103/PhysRev.174.1559. S2CID 123261579. Архивировано из оригинала (PDF) 2020-02-25.
- ^ Бардин, Джеймс М.; Пресс, Уильям Х.; Тьюкольский, Сол А. (1972). «Вращающиеся черные дыры: локально невращающиеся системы отсчета, извлечение энергии и скалярное синхротронное излучение». The Astrophysical Journal . 178 : 347. Bibcode : 1972ApJ...178..347B. doi : 10.1086/151796.
- ^ Фролов, Андрей В.; Фролов, Валерий П. (2014). "Жестко вращающиеся поверхности наблюдателя с нулевым угловым моментом в пространстве-времени Керра". Physical Review D. 90 ( 12): 124010. arXiv : 1408.6316 . Bibcode : 2014PhRvD..90l4010F. doi : 10.1103/PhysRevD.90.124010. S2CID 118417747.)
- ^ Риасуэло, Ален (декабрь 2020 г.). «Видеть относительность — III. Путешествие в метрике Керра к области отрицательной гравитации». International Journal of Modern Physics D . 29 (16): 2050109– 2050202. arXiv : 2008.04384 . Bibcode :2020IJMPD..2950109R. doi :10.1142/S0218271820501096. ISSN 0218-2718. S2CID 221095833.
- ^ Чандрасекар, С. (1983). Математическая теория черных дыр . Международная серия монографий по физике. Т. 69. С. 375.
- ^ Эндрю Гамильтон: Диаграммы Пенроуза для чёрных дыр (JILA Colorado)
- ^ Пенроуз 1968
- ^ Бичак, Джржи; Ледвинка, Томаш (1993). «Релятивистские диски как источники метрики Керра». Physical Review Letters . 71 (11): 1669– 1672. Bibcode : 1993PhRvL..71.1669B. doi : 10.1103/physrevlett.71.1669. PMID 10054468.
Дальнейшее чтение
- Wiltshire, David L.; Visser, Matt; Scott, Susan M. , ред. (2009). Пространство-время Керра: вращающиеся черные дыры в общей теории относительности . Кембридж: Cambridge University Press. ISBN 978-0-521-88512-6.
- Стефани, Ганс; Крамер, Дитрих; Маккаллум, Малкольм; Хоенселаерс, Корнелиус; Херлт, Эдуард (2003). Точные решения уравнений поля Эйнштейна . Кембридж: Cambridge University Press. ISBN 978-0-521-46136-8.
- Майнель, Рейнхард ; Ансорг, Маркус; Кляйнвахтер, Андреас; Нойгебауэр, Гернот; Петров, Дэвид (2008). Релятивистские фигуры равновесия. Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-86383-4.
- О'Нил, Барретт (1995). Геометрия черных дыр Керра . Уэллсли, Массачусетс: AK Peters. ISBN 978-1-56881-019-5.
- D'Inverno, Ray (1992). Введение в теорию относительности Эйнштейна . Оксфорд: Clarendon Press. ISBN 978-0-19-859686-8. Введение на продвинутом уровне бакалавриата см. в главе 19.
- Чандрасекар, С. (1992). Математическая теория черных дыр . Оксфорд: Clarendon Press. ISBN 978-0-19-850370-5. См. главы 6–10 для очень подробного изучения на уровне продвинутого магистра.
- Гриффитс, Дж. Б. (1991). Столкновение плоских волн в общей теории относительности . Оксфорд: Oxford University Press. ISBN 978-0-19-853209-5. См. главу 13 для модели Чандрасекара/Феррари CPW.
- Адлер, Рональд; Базен, Морис; Шиффер, Менахем (1975). Введение в общую теорию относительности (второе изд.). Нью-Йорк: McGraw-Hill. ISBN 978-0-07-000423-8. См. главу 7 .
- Пенроуз, Р. (1968). под ред. К. де Витта и Дж. Уиллера (ред.). Баттель Реконтр . У.А. Бенджамин, Нью-Йорк. п. 222.
- Перес, Алехандро; Морески, Освальдо М. (2000). «Характеристика точных решений с помощью асимптотических физических концепций». arXiv : gr-qc/0012100v1 .Характеристика трех стандартных семейств вакуумных решений, как отмечено выше.
- Сотириу, Томас П.; Апостолатос, Теохарис А. (2004). «Исправления и комментарии к мультипольным моментам осесимметричных электровакуумных пространств-времен». Класс. Квантовая гравитация . 21 (24): 5727– 5733. arXiv : gr-qc/0407064 . Bibcode : 2004CQGra..21.5727S. doi : 10.1088/0264-9381/21/24/003. S2CID 16858122.Дает релятивистские мультипольные моменты для вакуумов Эрнста (плюс электромагнитные и гравитационные релятивистские мультипольные моменты для заряженного обобщения).
- Картер, Б. (1971). «Осесимметричная черная дыра имеет только две степени свободы». Physical Review Letters . 26 (6): 331– 333. Bibcode : 1971PhRvL..26..331C. doi : 10.1103/PhysRevLett.26.331.
- Wald, RM (1984). Общая теория относительности . Чикаго: Издательство Чикагского университета. С. 312–324 . ISBN 978-0-226-87032-8.
- Керр, РП; Шильд, А. (2009). «Переиздание: Новый класс вакуумных решений уравнений поля Эйнштейна». Общая теория относительности и гравитация . 41 (10): 2485– 2499. Bibcode : 2009GReGr..41.2485K. doi : 10.1007/s10714-009-0857-z. S2CID 361088.
- Красински, Анджей; Вердагер, Энрик; Керр, Рой Патрик (2009). «Редакционное примечание к: RP Kerr и A. Schild, Новый класс вакуумных решений уравнений поля Эйнштейна». Общая теория относительности и гравитация . 41 (10): 2469– 2484. Bibcode : 2009GReGr..41.2469K. doi : 10.1007/s10714-009-0856-0 .«... Эта заметка призвана стать руководством для тех читателей, которые желают проверить все детали [вывода решения Керра]...»









































































![{\displaystyle {\ddot {x}}+i{\ddot {y}}=4iMa{\frac {r}{\Sigma ^{2}}}W\left[{\dot {x}}+i{\dot {y}}-{\frac {x+iy}{r}}{\dot {r}}\right]-M(x+iy)\left({\frac {4r^{2}}{\Sigma }}-1\right){\frac {Ca^{2}W^{2}}{r\Sigma ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fe5085203cdf9ef96c35da0c12f7ef468f7e0c4)



















![{\displaystyle M_{n}=M[ia]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/893371be1a5049a3794f9a6c348145599d2e5db2)



