Черная дыра
Черная дыра — это область пространства-времени , где гравитация настолько сильна, что ничто, даже свет и другие электромагнитные волны , не способно обладать достаточной энергией, чтобы вырваться из нее. [2] Общая теория относительности Эйнштейна предсказывает, что достаточно компактная масса может деформировать пространство-время, образуя черную дыру. [3] [4] Граница невыхода называется горизонтом событий . Черная дыра оказывает большое влияние на судьбу и обстоятельства объекта, пересекающего ее, но у нее нет локально обнаруживаемых особенностей согласно общей теории относительности. [ 5] Во многих отношениях черная дыра ведет себя как идеальное черное тело , поскольку она не отражает свет. [6] [7] Квантовая теория поля в искривленном пространстве-времени предсказывает, что горизонты событий испускают излучение Хокинга с тем же спектром , что и черное тело с температурой, обратно пропорциональной его массе. Эта температура составляет порядка миллиардных долей кельвина для звездных черных дыр , что делает по существу невозможным прямое наблюдение.
Объекты, гравитационные поля которых слишком сильны для того, чтобы свет мог их покинуть, были впервые рассмотрены в 18 веке Джоном Мичеллом и Пьером-Симоном Лапласом . [8] В 1916 году Карл Шварцшильд нашел первое современное решение общей теории относительности, которое характеризовало бы черную дыру. Благодаря его влиятельным исследованиям метрика Шварцшильда названа в его честь. Дэвид Финкельштейн в 1958 году впервые опубликовал интерпретацию «черной дыры» как области пространства, из которой ничто не может покинуть ее. Черные дыры долгое время считались математической диковинкой; только в 1960-х годах теоретические работы показали, что они являются общим предсказанием общей теории относительности. Открытие нейтронных звезд Джоселин Белл Бернелл в 1967 году вызвало интерес к гравитационно сколлапсировавшим компактным объектам как к возможной астрофизической реальности. Первой известной черной дырой была Cygnus X-1 , идентифицированная несколькими исследователями независимо в 1971 году. [9] [10]
Черные дыры звездной массы образуются, когда массивные звезды коллапсируют в конце своего жизненного цикла. После того, как черная дыра образовалась, она может расти, поглощая массу из своего окружения. Сверхмассивные черные дыры массой в миллионы солнечных ( M ☉ ) могут образовываться, поглощая другие звезды и сливаясь с другими черными дырами, или путем прямого коллапса газовых облаков . Существует консенсус, что сверхмассивные черные дыры существуют в центрах большинства галактик .
Присутствие черной дыры можно вывести по ее взаимодействию с другой материей и с электромагнитным излучением, таким как видимый свет. Любая материя, которая падает на черную дыру, может образовать внешний аккреционный диск , нагреваемый трением , образуя квазары , одни из самых ярких объектов во Вселенной. Звезды, проходящие слишком близко к сверхмассивной черной дыре, могут быть измельчены в потоки, которые сияют очень ярко, прежде чем будут «проглочены». [11] Если другие звезды вращаются вокруг черной дыры, их орбиты можно использовать для определения массы и местоположения черной дыры. Такие наблюдения можно использовать для исключения возможных альтернатив, таких как нейтронные звезды. Таким образом, астрономы идентифицировали множество кандидатов на роль звездной черной дыры в двойных системах и установили, что радиоисточник, известный как Стрелец A* , в ядре галактики Млечный Путь , содержит сверхмассивную черную дыру массой около 4,3 миллиона солнечных .
История
Идея о теле настолько большом, что даже свет не может вырваться, была кратко предложена английским астрономом-пионером и священнослужителем Джоном Мичеллом в письме, опубликованном в ноябре 1784 года. Упрощенные расчеты Мичелла предполагали, что такое тело может иметь ту же плотность, что и Солнце, и пришли к выводу, что оно образуется, когда диаметр звезды превышает диаметр Солнца в 500 раз, а ее поверхностная скорость убегания превышает обычную скорость света. Мичелл правильно заметил, что такие сверхмассивные, но не излучающие тела могут быть обнаружены по их гравитационному воздействию на близлежащие видимые тела. [8] [12] [13] Ученые того времени изначально были взволнованы предположением о том, что гигантские, но невидимые «темные звезды» могут скрываться на виду, но энтузиазм угас, когда волновая природа света стала очевидной в начале девятнадцатого века, [14] поскольку если бы свет был волной, а не частицей, было бы неясно, какое влияние гравитация окажет на выходящие световые волны, если таковое имеется. [8] [13]
Современная теория гравитации, общая теория относительности, дискредитирует идею Мичелла о том, что луч света вылетает непосредственно с поверхности сверхмассивной звезды, замедляется гравитацией звезды, останавливается и затем свободно падает обратно на поверхность звезды. [15] Вместо этого само пространство-время искривлено таким образом, что геодезическая , по которой движется свет, никогда не покидает поверхность «звезды» (черной дыры).
Общая теория относительности
| Общая теория относительности |
|---|
 |
В 1915 году Альберт Эйнштейн разработал свою общую теорию относительности , ранее показав, что гравитация действительно влияет на движение света. Всего несколько месяцев спустя Карл Шварцшильд нашел решение уравнений поля Эйнштейна , которое описывает гравитационное поле точечной массы и сферической массы. [16] [17] Через несколько месяцев после Шварцшильда, Иоганнес Дросте , ученик Хендрика Лоренца , независимо дал то же самое решение для точечной массы и более подробно описал ее свойства. [18] [19] Это решение имело своеобразное поведение в том, что сейчас называется радиусом Шварцшильда , где оно становилось сингулярным , что означало, что некоторые члены в уравнениях Эйнштейна становились бесконечными. Природа этой поверхности в то время была не совсем понятна.
В 1924 году Артур Эддингтон показал, что сингулярность исчезает после изменения координат. В 1933 году Жорж Леметр понял, что это означает, что сингулярность на радиусе Шварцшильда является нефизической координатной сингулярностью . [20] Артур Эддингтон прокомментировал возможность существования звезды с массой, сжатой до радиуса Шварцшильда, в книге 1926 года, отметив, что теория Эйнштейна позволяет нам исключить слишком большую плотность для видимых звезд, таких как Бетельгейзе, потому что «звезда радиусом 250 миллионов км не могла бы иметь такую высокую плотность, как Солнце. Во-первых, сила гравитации была бы настолько велика, что свет не смог бы вырваться из нее, лучи падали бы обратно на звезду, как камень на землю. Во-вторых, красное смещение спектральных линий было бы настолько велико, что спектр был бы смещен из существования. В-третьих, масса создавала бы такую большую кривизну метрики пространства-времени, что пространство сомкнулось бы вокруг звезды, оставив нас снаружи (т. е. нигде)». [21] [22]
В 1931 году Субраманьян Чандрасекар рассчитал, используя специальную теорию относительности, что невращающееся тело электронно-вырожденной материи выше определенной предельной массы (теперь называемой пределом Чандрасекара при 1,4 M ☉ ) не имеет устойчивых решений. [23] Его аргументы были опровергнуты многими его современниками, такими как Эддингтон и Лев Ландау , которые утверждали, что какой-то пока неизвестный механизм остановит коллапс. [24] Они были отчасти правы: белый карлик, немного более массивный, чем предел Чандрасекара, коллапсирует в нейтронную звезду , [25] которая сама по себе стабильна.
В 1939 году Роберт Оппенгеймер и другие предсказали, что нейтронные звезды выше другого предела, предела Толмена–Оппенгеймера–Волкова , будут коллапсировать дальше по причинам, представленным Чандрасекаром, и пришли к выводу, что никакой закон физики, вероятно, не вмешается и не остановит по крайней мере некоторые звезды от коллапса в черные дыры. [26] Их первоначальные расчеты, основанные на принципе исключения Паули , дали его как 0,7 M ☉ . Последующее рассмотрение отталкивания нейтронов, опосредованного сильным взаимодействием, повысило оценку примерно до 1,5 M ☉ до 3,0 M ☉ . [27] Наблюдения за слиянием нейтронных звезд GW170817 , которое, как полагают, вскоре породило черную дыру, уточнили оценку предела TOV до ~2,17 M ☉ . [28] [29] [30] [31] [32]
Оппенгеймер и его соавторы интерпретировали сингулярность на границе радиуса Шварцшильда как указание на то, что это была граница пузыря, в котором время остановилось. Это допустимая точка зрения для внешних наблюдателей, но не для наблюдателей, падающих внутрь. Гипотетические коллапсировавшие звезды были названы «замороженными звездами», потому что внешний наблюдатель увидел бы поверхность звезды, замороженную во времени в тот момент, когда ее коллапс перенесет ее на радиус Шварцшильда. [33]
Также в 1939 году Эйнштейн попытался доказать невозможность существования черных дыр в своей публикации «О стационарной системе со сферической симметрией, состоящей из многих гравитирующих масс», используя свою общую теорию относительности для защиты своего аргумента. [34] Несколько месяцев спустя Оппенгеймер и его студент Хартланд Снайдер представили модель Оппенгеймера–Снайдера в своей статье «О непрерывном гравитационном сокращении» [35] , которая предсказала существование черных дыр. В статье, которая не ссылалась на недавнюю публикацию Эйнштейна, Оппенгеймер и Снайдер использовали собственную теорию относительности Эйнштейна, чтобы показать условия, при которых может возникнуть черная дыра, впервые в современной физике. [34]
Золотой век
В 1958 году Дэвид Финкельштейн определил поверхность Шварцшильда как горизонт событий , «совершенную однонаправленную мембрану: причинные влияния могут пересекать ее только в одном направлении». [36] Это не противоречило строго результатам Оппенгеймера, но расширяло их, включая точку зрения падающих наблюдателей. Решение Финкельштейна расширило решение Шварцшильда для будущего наблюдателей, падающих в черную дыру. Полное расширение уже было найдено Мартином Крускалом , которого настоятельно просили опубликовать его. [37]
Эти результаты появились в начале золотого века общей теории относительности , который был отмечен общей теорией относительности и черными дырами, ставшими основными объектами исследований. Этому процессу способствовало открытие пульсаров Джоселин Белл Бернелл в 1967 году [38] [39] , которые к 1969 году оказались быстро вращающимися нейтронными звездами. [40] До этого времени нейтронные звезды, как и черные дыры, считались просто теоретическими диковинками; но открытие пульсаров показало их физическую значимость и подстегнуло дальнейший интерес ко всем типам компактных объектов, которые могли быть образованы гравитационным коллапсом. [41]
В этот период были найдены более общие решения для черной дыры. В 1963 году Рой Керр нашел точное решение для вращающейся черной дыры . Два года спустя Эзра Ньюман нашел осесимметричное решение для черной дыры, которая одновременно вращается и электрически заряжена . [42] Благодаря работам Вернера Израиля , [43] Брэндона Картера , [44] [45] и Дэвида Робинсона [46] появилась теорема об отсутствии волос , утверждающая, что стационарное решение для черной дыры полностью описывается тремя параметрами метрики Керра–Ньюмана : массой , угловым моментом и электрическим зарядом. [47]
Сначала предполагалось, что странные особенности решений для черных дыр являются патологическими артефактами из-за наложенных условий симметрии, и что сингулярности не будут появляться в общих ситуациях. Этой точки зрения придерживались, в частности, Владимир Белинский , Исаак Халатников и Евгений Лифшиц , которые пытались доказать, что в общих решениях не возникает никаких сингулярностей. Однако в конце 1960-х годов Роджер Пенроуз [48] и Стивен Хокинг использовали глобальные методы, чтобы доказать, что сингулярности появляются в общем виде. [49] За эту работу Пенроуз получил половину Нобелевской премии по физике 2020 года , Хокинг умер в 2018 году. [50] Основываясь на наблюдениях в Гринвиче и Торонто в начале 1970-х годов, Cygnus X-1 , галактический рентгеновский источник, открытый в 1964 году, стал первым астрономическим объектом, который общепринято считается черной дырой. [51] [52]
Работа Джеймса Бардина , Джейкоба Бекенштейна , Картера и Хокинга в начале 1970-х годов привела к формулировке термодинамики черных дыр . [53] Эти законы описывают поведение черной дыры в тесной аналогии с законами термодинамики, связывая массу с энергией, площадь с энтропией и поверхностную гравитацию с температурой . Аналогия была завершена, когда Хокинг в 1974 году показал, что квантовая теория поля подразумевает, что черные дыры должны излучать как черное тело с температурой, пропорциональной поверхностной гравитации черной дыры, предсказывая эффект, теперь известный как излучение Хокинга . [54]
Наблюдение
11 февраля 2016 года научное сотрудничество LIGO и сотрудничество Virgo объявили о первом прямом обнаружении гравитационных волн , что представляет собой первое наблюдение слияния черных дыр. [55] 10 апреля 2019 года было опубликовано первое прямое изображение черной дыры и ее окрестностей, после наблюдений, сделанных телескопом Event Horizon Telescope (EHT) в 2017 году за сверхмассивной черной дырой в галактическом центре Мессье 87. [56] [57] [58] По состоянию на 2023 год ближайшее известное тело, которое считается черной дырой, Gaia BH1 , находится на расстоянии около 1560 световых лет (480 парсеков ) от нас. [59] Хотя до сих пор в Млечном Пути было обнаружено всего несколько десятков черных дыр , считается, что их сотни миллионов, большинство из которых являются одиночными и не вызывают испускания излучения. [60] Поэтому их можно обнаружить только с помощью гравитационного линзирования .[update]
Этимология
Джон Мичелл использовал термин «темная звезда» в письме Генри Кавендишу от ноября 1783 года [ требуется ссылка ] , а в начале 20-го века физики использовали термин «гравитационно коллапсирующий объект». Научный писатель Марсия Бартусяк прослеживает термин «черная дыра» до физика Роберта Х. Дике , который в начале 1960-х годов, как сообщается, сравнил это явление с Черной дырой Калькутты , печально известной как тюрьма, куда люди попадали, но никогда не выходили живыми. [61]
Термин «черная дыра» был использован в печати журналами Life и Science News в 1963 году [61], а также научным журналистом Энн Юинг в ее статье « Черные дыры» в космосе» от 18 января 1964 года, которая представляла собой отчет о заседании Американской ассоциации содействия развитию науки, состоявшемся в Кливленде, штат Огайо. [62] [63]
В декабре 1967 года один из студентов, как сообщается, предложил фразу «черная дыра» на лекции Джона Уиллера ; [62] Уиллер принял этот термин из-за его краткости и «рекламной ценности», и он быстро прижился, [64] что заставило некоторых приписать Уиллеру создание этой фразы. [65]
Свойства и структура
Теорема об отсутствии волос постулирует, что после достижения устойчивого состояния после формирования черная дыра имеет только три независимых физических свойства: массу, электрический заряд и угловой момент; в остальном черная дыра лишена каких-либо особенностей. Если гипотеза верна, то любые две черные дыры, которые имеют одинаковые значения этих свойств или параметров, неотличимы друг от друга. Степень, в которой гипотеза верна для реальных черных дыр в соответствии с законами современной физики, в настоящее время является нерешенной проблемой. [47]
Эти свойства являются особенными, поскольку они видны снаружи черной дыры. Например, заряженная черная дыра отталкивает другие одноименные заряды, как и любой другой заряженный объект. Аналогично, общая масса внутри сферы, содержащей черную дыру, может быть найдена с помощью гравитационного аналога закона Гаусса (через массу ADM ), вдали от черной дыры. [66] Аналогично, угловой момент (или спин) может быть измерен издалека с помощью увлечения системы отсчета гравитомагнитным полем , например, с помощью эффекта Лензе–Тирринга . [67]

Когда объект падает в черную дыру, любая информация о форме объекта или распределении заряда на нем равномерно распределяется вдоль горизонта черной дыры и теряется для внешних наблюдателей. Поведение горизонта в этой ситуации представляет собой диссипативную систему , которая очень похожа на поведение проводящей эластичной мембраны с трением и электрическим сопротивлением — мембранная парадигма . [68] Это отличается от других полевых теорий, таких как электромагнетизм, которые не имеют никакого трения или сопротивления на микроскопическом уровне, потому что они обратимы во времени . [69] [70]
Поскольку черная дыра в конечном итоге достигает устойчивого состояния всего с тремя параметрами, нет способа избежать потери информации о начальных условиях: гравитационное и электрическое поля черной дыры дают очень мало информации о том, что вошло. Теряемая информация включает в себя все величины, которые не могут быть измерены вдали от горизонта черной дыры, включая приблизительно сохраняющиеся квантовые числа, такие как общее число барионов и число лептонов . Такое поведение настолько загадочно, что его назвали парадоксом потери информации черной дырой . [69] [71]
Физические свойства
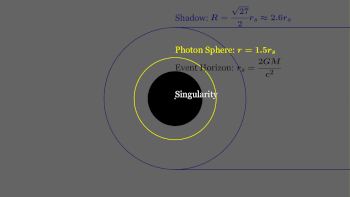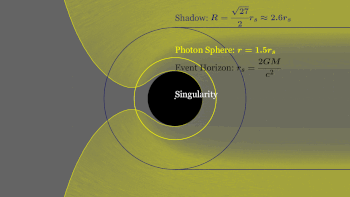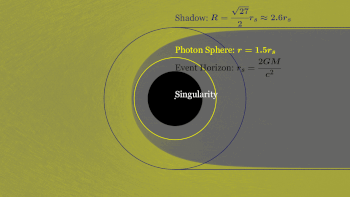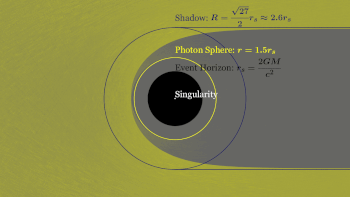
Простейшие статические черные дыры имеют массу, но не имеют ни электрического заряда, ни углового момента. Эти черные дыры часто называют черными дырами Шварцшильда в честь Карла Шварцшильда, который открыл это решение в 1916 году. [17] Согласно теореме Биркгофа , это единственное вакуумное решение , которое является сферически симметричным . [72] Это означает, что нет никакой наблюдаемой разницы на расстоянии между гравитационным полем такой черной дыры и полем любого другого сферического объекта той же массы. Популярное представление о черной дыре, «засасывающей все» в своем окружении, поэтому верно только вблизи горизонта черной дыры; вдали внешнее гравитационное поле идентично полю любого другого тела той же массы. [73]
Существуют также решения, описывающие более общие черные дыры. Невращающиеся заряженные черные дыры описываются метрикой Рейсснера–Нордстрема , в то время как метрика Керра описывает незаряженную вращающуюся черную дыру. Наиболее общее известное решение для стационарной черной дыры — это метрика Керра–Ньюмана, которая описывает черную дыру как с зарядом, так и с угловым моментом. [74]
В то время как масса черной дыры может принимать любое положительное значение, заряд и момент импульса ограничены массой. Ожидается, что полный электрический заряд Q и полный момент импульса J будут удовлетворять неравенству
для черной дыры с массой M. Черные дыры с минимально возможной массой, удовлетворяющей этому неравенству, называются экстремальными . Решения уравнений Эйнштейна, которые нарушают это неравенство, существуют, но они не обладают горизонтом событий. Эти решения имеют так называемые голые сингулярности , которые можно наблюдать извне, и поэтому считаются нефизическими . Гипотеза космической цензуры исключает образование таких сингулярностей, когда они создаются посредством гравитационного коллапса реальной материи . [3] Это подтверждается численным моделированием. [75]
Из-за относительно большой силы электромагнитного взаимодействия , черные дыры, образующиеся при коллапсе звезд, как ожидается, сохранят почти нейтральный заряд звезды. Однако ожидается, что вращение будет универсальной чертой компактных астрофизических объектов. Кандидат в черные дыры, двойной рентгеновский источник GRS 1915+105 [76], по-видимому, имеет угловой момент, близкий к максимально допустимому значению. Этот предел без заряда [77]
позволяя определить безразмерный параметр спина таким образом, что [77]
- [77] [Примечание 1]
| Сорт | Приблизительная масса | Приблизительный радиус |
|---|---|---|
| Сверхмассивная черная дыра | 109–1011 М ☉ | >1000 а.е. |
| Сверхмассивная черная дыра | 106–109 М ☉ | 0,001–400 а.е. |
| Черная дыра средней массы | 102–105 М ☉ | 10 3 км ≈ R Земля |
| Звездная черная дыра | 2-150 М ☉ | 30 км |
| Микро черная дыра | до М Луны | до 0,1 мм |
Черные дыры обычно классифицируются по их массе, независимой от углового момента J. Размер черной дыры, определяемый радиусом горизонта событий или радиусом Шварцшильда, пропорционален массе M через
где r s — радиус Шварцшильда, а M ☉ — масса Солнца . [79] Для черной дыры с ненулевым спином и/или электрическим зарядом радиус меньше, [Примечание 2] до тех пор, пока экстремальная черная дыра не может иметь горизонт событий, близкий к [80]
Горизонт событий
Определяющей чертой черной дыры является появление горизонта событий — границы в пространстве-времени , через которую материя и свет могут проходить только внутрь к массе черной дыры. Ничто, даже свет, не может вырваться из-под горизонта событий. [82] [83] Горизонт событий называется так потому, что если событие происходит внутри границы, информация об этом событии не может достичь внешнего наблюдателя, что делает невозможным определение того, произошло ли такое событие. [84]
Как предсказывает общая теория относительности, наличие массы деформирует пространство-время таким образом, что траектории частиц изгибаются в сторону массы. [85] На горизонте событий черной дыры эта деформация становится настолько сильной, что не остается путей, ведущих от черной дыры. [86]
Для удаленного наблюдателя часы вблизи черной дыры будут казаться идущими медленнее, чем те, что находятся дальше от черной дыры. [87] Из-за этого эффекта, известного как гравитационное замедление времени , объект, падающий в черную дыру, кажется замедляющимся по мере приближения к горизонту событий, и ему требуется бесконечное количество времени, чтобы достичь его. [88] В то же время все процессы на этом объекте замедляются с точки зрения неподвижного внешнего наблюдателя, в результате чего любой свет, испускаемый объектом, кажется более красным и тусклым, эффект, известный как гравитационное красное смещение . [89] В конце концов, падающий объект исчезает, пока его больше нельзя увидеть. Обычно этот процесс происходит очень быстро, и объект исчезает из виду менее чем за секунду. [90]
С другой стороны, неразрушимые наблюдатели, падающие в черную дыру, не замечают ни одного из этих эффектов, пересекая горизонт событий. Согласно их собственным часам, которые, как им кажется, идут нормально, они пересекают горизонт событий за конечное время, не замечая никакого сингулярного поведения; в классической общей теории относительности невозможно определить местоположение горизонта событий из локальных наблюдений из-за принципа эквивалентности Эйнштейна . [91] [92]
Топология горизонта событий черной дыры в состоянии равновесия всегда сферическая. [ Примечание 4] [95] Для невращающихся (статичных) черных дыр геометрия горизонта событий точно сферическая, тогда как для вращающихся черных дыр горизонт событий сплющенный. [96] [97] [98]
Сингулярность
В центре черной дыры, как описано общей теорией относительности, может находиться гравитационная сингулярность , область, где кривизна пространства-времени становится бесконечной. [99] Для невращающейся черной дыры эта область принимает форму одной точки; для вращающейся черной дыры она размазывается, образуя кольцевую сингулярность , которая лежит в плоскости вращения. [100] В обоих случаях сингулярная область имеет нулевой объем. Можно также показать, что сингулярная область содержит всю массу решения черной дыры. [101] Таким образом, сингулярную область можно рассматривать как имеющую бесконечную плотность . [102]
Наблюдатели, падающие в черную дыру Шварцшильда (т. е. не вращающуюся и не заряженную), не могут избежать попадания в сингулярность, как только они пересекут горизонт событий. Они могут продлить этот опыт, ускоряясь, чтобы замедлить свое падение, но только до определенного предела. [103] Когда они достигают сингулярности, они сжимаются до бесконечной плотности, и их масса добавляется к общей массе черной дыры. Прежде чем это произойдет, они будут разорваны на части растущими приливными силами в процессе, иногда называемом спагеттификацией или «эффектом лапши». [104]
В случае заряженной (Рейсснера-Нордстрема) или вращающейся (Керра) черной дыры можно избежать сингулярности. Расширение этих решений насколько это возможно, раскрывает гипотетическую возможность выхода из черной дыры в другое пространство-время, где черная дыра действует как червоточина . [ 105] Однако возможность путешествия в другую вселенную является лишь теоретической, поскольку любое возмущение уничтожило бы эту возможность. [106] Также, по-видимому, возможно следовать замкнутым времениподобным кривым (возвращаясь к собственному прошлому) вокруг сингулярности Керра, что приводит к проблемам с причинностью, таким как парадокс дедушки . [107] Ожидается, что ни один из этих своеобразных эффектов не сохранится при надлежащем квантовом рассмотрении вращающихся и заряженных черных дыр. [108]
Появление сингулярностей в общей теории относительности обычно воспринимается как сигнал о крахе теории. [109] Этот крах, однако, ожидаем; он происходит в ситуации, когда квантовые эффекты должны описывать эти действия, из-за чрезвычайно высокой плотности и, следовательно, взаимодействия частиц. На сегодняшний день не удалось объединить квантовые и гравитационные эффекты в единую теорию, хотя существуют попытки сформулировать такую теорию квантовой гравитации . Обычно ожидается, что такая теория не будет содержать никаких сингулярностей. [110] [111]
Фотонная сфера
Фотонная сфера — это сферическая граница, где фотоны, двигающиеся по касательным к этой сфере, будут пойманы в нестабильную, но круговую орбиту вокруг черной дыры. [112] Для невращающихся черных дыр радиус фотонной сферы в 1,5 раза больше радиуса Шварцшильда. Их орбиты будут динамически нестабильными , поэтому любое небольшое возмущение, такое как частица падающей материи, вызовет нестабильность, которая будет расти со временем, либо устанавливая фотон на внешнюю траекторию, заставляя его покинуть черную дыру, либо на внутреннюю спираль, где он в конечном итоге пересечет горизонт событий. [113]
Хотя свет все еще может вырваться из фотонной сферы, любой свет, пересекающий фотонную сферу по входящей траектории, будет захвачен черной дырой. Следовательно, любой свет, достигающий внешнего наблюдателя из фотонной сферы, должен быть испущен объектами между фотонной сферой и горизонтом событий. [113] Для черной дыры Керра радиус фотонной сферы зависит от параметра спина и от деталей фотонной орбиты, которая может быть прямой (фотон вращается в том же направлении, что и спин черной дыры) или ретроградной. [114] [115]
Эргосфера
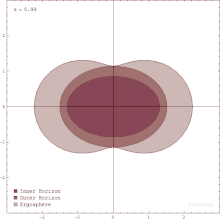
Вращающиеся черные дыры окружены областью пространства-времени, в которой невозможно стоять на месте, называемой эргосферой. Это результат процесса, известного как перетаскивание кадров ; общая теория относительности предсказывает, что любая вращающаяся масса будет иметь тенденцию слегка «перетаскиваться» по пространству-времени, непосредственно окружающему ее. Любой объект вблизи вращающейся массы будет иметь тенденцию начинать движение в направлении вращения. Для вращающейся черной дыры этот эффект настолько силен вблизи горизонта событий, что объект должен был бы двигаться быстрее скорости света в противоположном направлении, чтобы просто стоять на месте. [117]
Эргосфера черной дыры — это объем, ограниченный горизонтом событий черной дыры и эргоповерхностью , которая совпадает с горизонтом событий на полюсах, но находится на гораздо большем расстоянии вокруг экватора. [116]
Объекты и излучение могут покидать эргосферу обычным образом. Благодаря процессу Пенроуза объекты могут выходить из эргосферы с большей энергией, чем они вошли. Дополнительная энергия берется из энергии вращения черной дыры. Тем самым вращение черной дыры замедляется. [118] Разновидность процесса Пенроуза в присутствии сильных магнитных полей, процесс Блэндфорда-Знаека считается вероятным механизмом для огромной светимости и релятивистских струй квазаров и других активных ядер галактик .
Самая внутренняя устойчивая круговая орбита (ISCO)
В ньютоновской гравитации тестовые частицы могут стабильно вращаться на произвольных расстояниях от центрального объекта. Однако в общей теории относительности существует внутренняя устойчивая круговая орбита (часто называемая ISCO), для которой любые бесконечно малые внутренние возмущения круговой орбиты приведут к скручиванию в черную дыру, а любые внешние возмущения, в зависимости от энергии, приведут к скручиванию в, стабильному вращению между апастроном и периастроном или уходу в бесконечность. [119] Местоположение ISCO зависит от спина черной дыры, в случае черной дыры Шварцшильда (спин ноль) это:
и уменьшается с увеличением спина черной дыры для частиц, вращающихся в том же направлении, что и спин. [120]
Погружающаяся область
Последняя наблюдаемая область пространства-времени вокруг черной дыры называется областью погружения. В этой области материя больше не может следовать по круговым орбитам или остановить окончательное падение в черную дыру. Вместо этого она будет стремительно падать в черную дыру со скоростью, близкой к скорости света. [121] [122]
Формирование и эволюция
Учитывая странный характер черных дыр, долгое время ставился под сомнение, могут ли такие объекты действительно существовать в природе или они являются просто патологическими решениями уравнений Эйнштейна. Сам Эйнштейн ошибочно считал, что черные дыры не образуются, поскольку он считал, что угловой момент коллапсирующих частиц стабилизирует их движение на некотором радиусе. [123] Это привело к тому, что сообщество общей теории относительности на протяжении многих лет отвергало все результаты, свидетельствующие об обратном. Однако меньшинство релятивистов продолжало утверждать, что черные дыры являются физическими объектами, [124] и к концу 1960-х годов они убедили большинство исследователей в этой области, что нет никаких препятствий для образования горизонта событий. [125]
Пенроуз продемонстрировал, что как только горизонт событий формируется, общая теория относительности без квантовой механики требует, чтобы внутри него образовалась сингулярность. [48] Вскоре после этого Хокинг показал, что многие космологические решения, описывающие Большой взрыв, имеют сингулярности без скалярных полей или другой экзотической материи . [ необходимо разъяснение ] Решение Керра , теорема об отсутствии волос и законы термодинамики черных дыр показали, что физические свойства черных дыр просты и понятны, что делает их достойными объектами для исследований. [126] Обычные черные дыры образуются в результате гравитационного коллапса тяжелых объектов, таких как звезды, но теоретически они также могут быть образованы другими процессами. [127] [128]
Гравитационный коллапс

Гравитационный коллапс происходит, когда внутреннее давление объекта недостаточно для сопротивления собственной гравитации объекта. Для звезд это обычно происходит либо потому, что у звезды осталось слишком мало «топлива», чтобы поддерживать ее температуру посредством звездного нуклеосинтеза , либо потому, что звезда, которая была бы стабильной, получает дополнительную материю таким образом, что это не повышает температуру ее ядра. В любом случае температура звезды уже недостаточно высока, чтобы предотвратить ее коллапс под собственным весом. [130]
Коллапс может быть остановлен давлением вырождения компонентов звезды, что позволяет сгущать материю в экзотическое более плотное состояние . Результатом является один из различных типов компактной звезды . Какой тип образуется, зависит от массы остатка исходной звезды, оставшейся, если внешние слои были сдуты (например, в сверхновой типа II ). Масса остатка, коллапсировавшего объекта, который переживает взрыв, может быть существенно меньше массы исходной звезды. Остатки, превышающие 5 M ☉, образуются звездами, которые имели массу более 20 M ☉ до коллапса. [130]
Если масса остатка превышает примерно 3–4 M ☉ (предел Толмена–Оппенгеймера–Волкова [26] ), либо потому, что исходная звезда была очень тяжелой, либо потому, что остаток собрал дополнительную массу за счет аккреции материи, даже давления вырождения нейтронов недостаточно, чтобы остановить коллапс. Ни один известный механизм (за исключением, возможно, давления вырождения кварков) не является достаточно мощным, чтобы остановить имплозию, и объект неизбежно коллапсирует, образуя черную дыру. [130]
Гравитационный коллапс тяжелых звезд, как предполагается, ответственен за образование черных дыр звездной массы . Звездообразование в ранней Вселенной могло привести к появлению очень массивных звезд, которые после своего коллапса могли бы произвести черные дыры массой до 103 M ☉ . Эти черные дыры могли быть зародышами сверхмассивных черных дыр, обнаруженных в центрах большинства галактик. [131] Кроме того, было высказано предположение, что массивные черные дыры с типичными массами ~105 M ☉ могли образоваться в результате прямого коллапса газовых облаков в молодой Вселенной. [127] Эти массивные объекты были предложены в качестве семян, которые в конечном итоге сформировали самые ранние квазары, наблюдаемые уже при красном смещении. [132] Некоторые кандидаты на такие объекты были обнаружены в наблюдениях за молодой Вселенной. [127]
Хотя большая часть энергии, высвобождаемой во время гравитационного коллапса, испускается очень быстро, внешний наблюдатель фактически не видит конца этого процесса. Несмотря на то, что коллапс занимает конечное количество времени в системе отсчета падающей материи, удаленный наблюдатель увидел бы, как падающая материя замедляется и останавливается прямо над горизонтом событий из-за гравитационного замедления времени. Свету от коллапсирующего материала требуется все больше и больше времени, чтобы достичь наблюдателя, при этом свет, испускаемый непосредственно перед формированием горизонта событий, задерживается на бесконечное количество времени. Таким образом, внешний наблюдатель никогда не видит формирования горизонта событий; вместо этого коллапсирующий материал, кажется, становится более тусклым и все более смещается в красную область спектра, в конечном итоге исчезая. [133]
Первичные черные дыры и Большой взрыв
Гравитационный коллапс требует большой плотности. В нынешнюю эпоху Вселенной такие высокие плотности встречаются только в звездах, но в ранней Вселенной вскоре после Большого взрыва плотности были намного больше, что, возможно, позволило создать черные дыры. Высокой плотности недостаточно для образования черных дыр, поскольку равномерное распределение массы не позволит массе скапливаться. Для того чтобы первичные черные дыры образовались в такой плотной среде, должны были быть начальные возмущения плотности, которые затем могли расти под действием собственной гравитации. Различные модели ранней Вселенной сильно различаются в своих предсказаниях масштаба этих флуктуаций. Различные модели предсказывают создание первичных черных дыр размером от массы Планка ( ≈1,2 × 10 19 ГэВ/ c 2 ≈2,2 × 10−8 кг ) до сотен тысяч масс Солнца. [ 128]
Несмотря на то, что ранняя вселенная была чрезвычайно плотной , она не сколлапсировала в черную дыру во время Большого взрыва, поскольку скорость расширения была больше, чем притяжение. Согласно теории инфляции, в начале и до конца инфляции существовала чистая отталкивающая гравитация. С тех пор поток Хаббла замедлялся плотностью энергии вселенной.
Модели гравитационного коллапса объектов относительно постоянного размера, таких как звезды , не обязательно применимы таким же образом к быстро расширяющемуся пространству, такому как Большой взрыв. [134]
Столкновения с высокой энергией
Гравитационный коллапс — не единственный процесс, который может создавать черные дыры. В принципе, черные дыры могут образовываться в столкновениях высокой энергии , которые достигают достаточной плотности. По состоянию на 2002 год такие события не были обнаружены, ни напрямую, ни косвенно как дефицит баланса массы в экспериментах на ускорителях частиц . [135] Это говорит о том, что должен быть нижний предел для массы черных дыр. Теоретически ожидается, что эта граница будет лежать около массы Планка, где квантовые эффекты, как ожидается, сделают недействительными предсказания общей теории относительности. [136]
Это поставило бы создание черных дыр вне досягаемости любого высокоэнергетического процесса, происходящего на Земле или вблизи нее. Однако некоторые разработки в области квантовой гравитации предполагают, что минимальная масса черной дыры может быть намного ниже: некоторые сценарии бранного мира , например, устанавливают границу так низко, как1 ТэВ/ c2 . [137] Это сделало бы возможным создание микрочерных дыр в столкновениях высоких энергий, которые происходят, когда космические лучи попадают в атмосферу Земли, или, возможно, в Большом адронном коллайдере в ЦЕРНе . Эти теории весьма спекулятивны, и создание черных дыр в этих процессах многими специалистами считается маловероятным. [138] Даже если микрочерные дыры могли бы образоваться, ожидается, что они испарятся примерно за 10−25 секунд , не представляя никакой угрозы для Земли. [139]
Рост
После того, как черная дыра образовалась, она может продолжать расти, поглощая дополнительную материю . Любая черная дыра будет постоянно поглощать газ и межзвездную пыль из своего окружения. Этот процесс роста является одним из возможных способов, посредством которого могли образоваться некоторые сверхмассивные черные дыры, хотя образование сверхмассивных черных дыр все еще остается открытой областью исследований. [131] Похожий процесс был предложен для образования черных дыр средней массы, обнаруженных в шаровых скоплениях . [140] Черные дыры также могут сливаться с другими объектами, такими как звезды или даже другие черные дыры. Считается, что это было важно, особенно на раннем этапе роста сверхмассивных черных дыр, которые могли образоваться из агрегации многих более мелких объектов. [131] Этот процесс также был предложен в качестве источника некоторых черных дыр средней массы. [141] [142]
Испарение
В 1974 году Хокинг предсказал, что черные дыры не полностью черные, а испускают небольшое количество теплового излучения при температуре ħc 3 /(8 πGM k B ); [54] этот эффект стал известен как излучение Хокинга. Применив квантовую теорию поля к статическому фону черной дыры, он определил, что черная дыра должна испускать частицы, которые демонстрируют идеальный спектр черного тела . После публикации Хокинга многие другие проверили результат с помощью различных подходов. [143] Если теория излучения черной дыры Хокинга верна, то ожидается, что черные дыры будут сжиматься и испаряться со временем, поскольку они теряют массу за счет испускания фотонов и других частиц. [54] Температура этого теплового спектра ( температура Хокинга ) пропорциональна поверхностной гравитации черной дыры, которая для черной дыры Шварцшильда обратно пропорциональна массе. Следовательно, большие черные дыры испускают меньше излучения, чем маленькие черные дыры. [144]
Звездная черная дыра массой 1 M ☉ имеет температуру Хокинга 62 нанокельвина . [145] Это намного меньше температуры 2,7 К реликтового излучения. Черные дыры звездной массы или большего размера получают больше массы от реликтового излучения, чем испускают через излучение Хокинга, и поэтому будут расти, а не сжиматься. [146] Чтобы иметь температуру Хокинга больше 2,7 К (и иметь возможность испаряться), черной дыре потребуется масса меньше Луны . Такая черная дыра будет иметь диаметр менее одной десятой миллиметра. [147]
Если черная дыра очень мала, ожидается, что эффекты излучения станут очень сильными. Черная дыра с массой автомобиля будет иметь диаметр около 10 −24 м и ей потребуется наносекунда, чтобы испариться, в течение которого она на короткое время будет иметь светимость более чем в 200 раз больше, чем у Солнца. Ожидается, что черные дыры с меньшей массой будут испаряться еще быстрее; например, черной дыре массой 1 ТэВ/ c 2 потребуется менее 10 −88 секунд, чтобы полностью испариться. Для такой маленькой черной дыры эффекты квантовой гравитации, как ожидается, будут играть важную роль и гипотетически могут сделать такую маленькую черную дыру стабильной, хотя текущие разработки в области квантовой гравитации не указывают на то, что это так. [148] [149]
Излучение Хокинга для астрофизической черной дыры, как предсказывают, будет очень слабым и, таким образом, его будет чрезвычайно трудно обнаружить с Земли. Однако возможным исключением является вспышка гамма-лучей, испускаемых на последней стадии испарения первичных черных дыр. Поиски таких вспышек оказались безуспешными и накладывают строгие ограничения на возможность существования маломассивных первичных черных дыр. [150] Космический гамма-телескоп НАСА «Ферми» , запущенный в 2008 году, продолжит поиск этих вспышек. [151]
Если черные дыры испаряются посредством излучения Хокинга, черная дыра солнечной массы испарится (начиная с того момента, как температура космического микроволнового фона упадет ниже температуры черной дыры) в течение периода 10 64 лет. [152] Сверхмассивная черная дыра с массой 1011 M ☉ испарится примерно через 2×10 100 лет. [153] Прогнозируется, что некоторые гигантские черные дыры во Вселенной продолжат расти, возможно, до 1014 M ☉ во время коллапса сверхскоплений галактик. Даже они испарились бы за время до 10 106 лет. [152]
Данные наблюдений
По своей природе черные дыры сами по себе не испускают никакого электромагнитного излучения, кроме гипотетического излучения Хокинга , поэтому астрофизики, ищущие черные дыры, должны, как правило, полагаться на косвенные наблюдения. Например, существование черной дыры иногда можно вывести, наблюдая ее гравитационное влияние на ее окружение. [154]
Прямая интерферометрия


Телескоп горизонта событий (EHT) — это активная программа, которая напрямую наблюдает за ближайшим окружением горизонтов событий черных дыр, например, за черной дырой в центре Млечного Пути. В апреле 2017 года EHT начал наблюдение за черной дырой в центре Мессье 87. [ 155] [156] «В общей сложности восемь радиообсерваторий на шести горах и четырех континентах наблюдали галактику в Деве с перерывами в течение 10 дней в апреле 2017 года», чтобы предоставить данные, дающие изображение в апреле 2019 года. [157]
После двух лет обработки данных EHT опубликовала первое прямое изображение черной дыры. А именно, сверхмассивной черной дыры, которая находится в центре вышеупомянутой галактики. [158] [159] То, что видно, — это не черная дыра, которая выглядит черной из-за потери всего света в этой темной области. Вместо этого, это газы на краю горизонта событий, отображаемые оранжевым или красным, которые определяют черную дыру. [160]
12 мая 2022 года EHT опубликовал первое изображение Стрельца A* , сверхмассивной черной дыры в центре галактики Млечный Путь . Опубликованное изображение отображало ту же кольцевую структуру и круглую тень , что и у черной дыры M87* , и изображение было создано с использованием тех же методов, что и для черной дыры M87. Процесс получения изображения для Стрельца A*, который более чем в тысячу раз меньше и менее массивен, чем M87*, был значительно более сложным из-за нестабильности его окружения. [161] Изображение Стрельца A* было частично размыто турбулентной плазмой на пути к галактическому центру, эффект, который препятствует разрешению изображения на более длинных волнах. [162]
Считается, что яркость этого материала в «нижней» половине обработанного изображения EHT вызвана доплеровским излучением , при котором материал, приближающийся к наблюдателю с релятивистской скоростью, воспринимается как более яркий, чем материал, удаляющийся. В случае черной дыры это явление подразумевает, что видимый материал вращается с релятивистской скоростью (>1000 км/с [2200000 миль/ч]), единственной скоростью, при которой возможно центробежно уравновесить огромное гравитационное притяжение сингулярности и, таким образом, оставаться на орбите выше горизонта событий. Такая конфигурация яркого материала подразумевает, что EHT наблюдал M87* с перспективы, захватывающей аккреционный диск черной дыры почти с ребра, поскольку вся система вращалась по часовой стрелке. [163] [164]
Экстремальное гравитационное линзирование, связанное с черными дырами, создает иллюзию перспективы, которая видит аккреционный диск сверху. В действительности большая часть кольца на изображении EHT была создана, когда свет, испускаемый дальней стороной аккреционного диска, огибал гравитационный колодец черной дыры и выходил наружу, что означает, что большинство возможных перспектив на M87* позволяют видеть весь диск, даже тот, что находится прямо за «тенью».
В 2015 году EHT обнаружил магнитные поля сразу за горизонтом событий Стрельца A* и даже распознал некоторые из их свойств. Линии поля, проходящие через аккреционный диск, представляли собой сложную смесь упорядоченных и запутанных. Теоретические исследования черных дыр предсказали существование магнитных полей. [165] [166]
В апреле 2023 года было представлено изображение тени черной дыры Мессье 87 и связанной с ней высокоэнергетической струи, впервые увиденных вместе. [167] [168]
Обнаружение гравитационных волн от слияния черных дыр

14 сентября 2015 года гравитационно-волновая обсерватория LIGO провела первое в истории успешное прямое наблюдение гравитационных волн . [55] [169] Сигнал соответствовал теоретическим предсказаниям для гравитационных волн, созданных слиянием двух черных дыр: одна с массой около 36 солнечных масс, а другая — около 29 солнечных масс. [55] [170] Это наблюдение дает наиболее конкретные доказательства существования черных дыр на сегодняшний день. Например, гравитационно-волновой сигнал предполагает, что разделение двух объектов до слияния составляло всего 350 км, или примерно в четыре раза больше радиуса Шварцшильда, соответствующего предполагаемым массам. Следовательно, объекты должны были быть чрезвычайно компактными, что делает черные дыры наиболее правдоподобной интерпретацией. [55]
Что еще более важно, сигнал, наблюдаемый LIGO, также включал начало кольцевого спада после слияния , сигнала, производимого, когда новообразованный компактный объект переходит в стационарное состояние. Можно утверждать, что кольцевой спад является наиболее прямым способом наблюдения за черной дырой. [171] Из сигнала LIGO можно извлечь частоту и время затухания доминирующей моды кольцевого спада. Из них можно вывести массу и угловой момент конечного объекта, которые соответствуют независимым предсказаниям из численного моделирования слияния. [172] Частота и время затухания доминирующей моды определяются геометрией фотонной сферы. Следовательно, наблюдение этой моды подтверждает наличие фотонной сферы; однако оно не может исключить возможные экзотические альтернативы черным дырам, которые достаточно компактны, чтобы иметь фотонную сферу. [171] [173]
Наблюдение также предоставляет первое наблюдательное свидетельство существования двойных черных дыр звездной массы. Более того, это первое наблюдательное свидетельство существования черных дыр звездной массы, весящих 25 солнечных масс или больше. [174]
С тех пор было замечено гораздо больше событий, связанных с гравитационными волнами . [175]
Звезды, вращающиеся вокруг Стрельца А*

Собственные движения звезд вблизи центра нашего Млечного Пути дают веские наблюдательные доказательства того, что эти звезды вращаются вокруг сверхмассивной черной дыры. [176] С 1995 года астрономы отслеживали движения 90 звезд, вращающихся вокруг невидимого объекта, совпадающего с радиоисточником Стрелец A*. Подгоняя их движения к кеплеровским орбитам , астрономы смогли сделать вывод в 1998 году, что2,6 × 10 6 M ☉ объект должен содержаться в объеме с радиусом 0,02 световых лет , чтобы вызвать движение этих звезд. [177]
С тех пор одна из звезд — S2 — завершила полный оборот по орбите. На основе орбитальных данных астрономы смогли уточнить расчеты массы до4,3 × 10 6 M ☉ и радиус менее 0,002 световых лет для объекта, вызывающего орбитальное движение этих звезд. [176] Верхний предел размера объекта все еще слишком велик, чтобы проверить, меньше ли он его радиуса Шварцшильда. Тем не менее, эти наблюдения настоятельно предполагают, что центральный объект является сверхмассивной черной дырой, поскольку нет других правдоподобных сценариев для ограничения столь большой невидимой массы в столь малом объеме. [177] Кроме того, есть некоторые наблюдательные свидетельства того, что этот объект может обладать горизонтом событий, особенностью, уникальной для черных дыр. [178]
Аккреция материи
Из-за сохранения углового момента [180] газ, падающий в гравитационную яму , созданную массивным объектом, обычно образует вокруг объекта дискообразную структуру. Художественные представления, такие как сопутствующее изображение черной дыры с короной, обычно изображают черную дыру так, как если бы она была плоским телом, скрывающим часть диска прямо за собой, но в действительности гравитационное линзирование сильно исказило бы изображение аккреционного диска. [181]
Внутри такого диска трение приведет к перемещению углового момента наружу, что позволит материи падать глубже внутрь, тем самым высвобождая потенциальную энергию и повышая температуру газа. [182]
Когда аккрецирующий объект является нейтронной звездой или черной дырой, газ во внутреннем аккреционном диске вращается по орбите с очень высокой скоростью из-за своей близости к компактному объекту . Результирующее трение настолько значительно, что оно нагревает внутренний диск до температур, при которых он испускает огромное количество электромагнитного излучения (в основном рентгеновского). Эти яркие источники рентгеновского излучения могут быть обнаружены телескопами. Этот процесс аккреции является одним из самых эффективных известных процессов производства энергии. До 40% массы покоя аккрецированного материала может быть испущено в виде излучения. [182] В ядерном синтезе только около 0,7% массы покоя будет испущено в виде энергии. Во многих случаях аккреционные диски сопровождаются релятивистскими струями , которые испускаются вдоль полюсов, которые уносят большую часть энергии. Механизм создания этих струй в настоящее время недостаточно изучен, отчасти из-за недостатка данных. [183]
Таким образом, многие из наиболее энергичных явлений Вселенной были приписаны аккреции материи на черных дырах. В частности, активные ядра галактик и квазары считаются аккреционными дисками сверхмассивных черных дыр. [184] Аналогично, рентгеновские двойные, как правило, считаются двойными звездными системами, в которых одна из двух звезд является компактным объектом, аккрецирующим материю со своего компаньона. [184] Также было высказано предположение, что некоторые сверхъяркие рентгеновские источники могут быть аккреционными дисками черных дыр промежуточной массы. [185]
Наблюдалось, что звезды разрываются приливными силами в непосредственной близости от сверхмассивных черных дыр в ядрах галактик, в так называемом событии приливного разрушения (TDE) . Часть материала разрушенной звезды образует аккреционный диск вокруг черной дыры, который испускает наблюдаемое электромагнитное излучение.
В ноябре 2011 года было сообщено о первом прямом наблюдении аккреционного диска квазара вокруг сверхмассивной черной дыры. [186] [187]
Рентгеновские двойные звезды

Рентгеновские двойные — это двойные звездные системы, которые испускают большую часть своего излучения в рентгеновской части спектра. Обычно считается, что эти рентгеновские излучения возникают, когда одна из звезд (компактный объект) аккрецирует вещество из другой (обычной) звезды. Присутствие обычной звезды в такой системе дает возможность изучить центральный объект и определить, может ли он быть черной дырой. [184]
Если такая система испускает сигналы, которые можно напрямую проследить до компактного объекта, то она не может быть черной дырой. Однако отсутствие такого сигнала не исключает возможности того, что компактный объект является нейтронной звездой. Изучая звезду-компаньона, часто можно получить орбитальные параметры системы и получить оценку массы компактного объекта. Если это намного больше предела Толмена-Оппенгеймера-Волкова (максимальной массы, которую звезда может иметь без коллапса), то объект не может быть нейтронной звездой и, как правило, ожидается, что он будет черной дырой. [184]
Первый сильный кандидат на роль черной дыры, Cygnus X-1 , был обнаружен таким образом Чарльзом Томасом Болтоном [188] , Луизой Вебстер и Полом Мурдином [189] в 1972 году. [190] [191] Оставались некоторые сомнения из-за неопределенностей, возникающих из-за того, что звезда-компаньон намного тяжелее кандидата на роль черной дыры. В настоящее время лучшие кандидаты на роль черных дыр находятся в классе рентгеновских двойных систем, называемых мягкими рентгеновскими транзиентами. В этом классе систем звезда-компаньон имеет относительно небольшую массу, что позволяет более точно оценить массу черной дыры. Эти системы активно испускают рентгеновские лучи всего несколько месяцев каждые 10–50 лет. В период слабого рентгеновского излучения, называемый спокойствием, аккреционный диск чрезвычайно слаб, что позволяет проводить детальные наблюдения за звездой-компаньоном в течение этого периода. Одним из лучших таких кандидатов является V404 Cygni [184 ]
Квазипериодические колебания
Рентгеновские излучения аккреционных дисков иногда мерцают на определенных частотах. Эти сигналы называются квазипериодическими колебаниями и, как полагают, вызываются материалом, движущимся вдоль внутреннего края аккреционного диска (самая внутренняя устойчивая круговая орбита). Таким образом, их частота связана с массой компактного объекта. Таким образом, их можно использовать в качестве альтернативного способа определения массы кандидатов в черные дыры. [192]
Ядра галактик

Астрономы используют термин «активная галактика» для описания галактик с необычными характеристиками, такими как необычное спектральное излучение и очень сильное радиоизлучение. Теоретические и наблюдательные исследования показали, что активность в этих активных ядрах галактик (AGN) может быть объяснена наличием сверхмассивных черных дыр, которые могут быть в миллионы раз массивнее звездных. Модели этих AGN состоят из центральной черной дыры, которая может быть в миллионы или миллиарды раз массивнее Солнца ; диска межзвездного газа и пыли, называемого аккреционным диском; и двух струй, перпендикулярных аккреционному диску. [194] [195]
Хотя ожидается, что сверхмассивные черные дыры будут обнаружены в большинстве активных галактических ядер, только ядра некоторых галактик были более тщательно изучены в попытках как идентифицировать, так и измерить фактические массы кандидатов в центральные сверхмассивные черные дыры. Некоторые из наиболее известных галактик с кандидатами в сверхмассивные черные дыры включают галактику Андромеды , M32 , M87 , NGC 3115 , NGC 3377 , NGC 4258 , NGC 4889 , NGC 1277 , OJ 287 , APM 08279+5255 и галактику Сомбреро . [196]
В настоящее время широко признано, что центр почти каждой галактики, а не только активной, содержит сверхмассивную черную дыру. [197] Тесная наблюдательная корреляция между массой этой дыры и дисперсией скоростей балджа родительской галактики , известная как соотношение M–сигма , настоятельно предполагает связь между образованием черной дыры и образованием самой галактики. [198]
Микролинзирование
Другой способ проверки природы черной дыры объекта — наблюдение эффектов, вызванных сильным гравитационным полем в их окрестностях. Одним из таких эффектов является гравитационное линзирование: деформация пространства-времени вокруг массивного объекта приводит к отклонению световых лучей, например, при прохождении света через оптическую линзу . Были проведены наблюдения слабого гравитационного линзирования, при котором световые лучи отклоняются всего на несколько угловых секунд . Микролинзирование происходит, когда источники неразрешены, и наблюдатель видит небольшое увеличение яркости. На рубеже тысячелетий были обнаружены первые 3 кандидата на черные дыры таким образом [199] [200] , а в январе 2022 года астрономы сообщили о первом подтвержденном обнаружении события микролинзирования от изолированной черной дыры. [201]
Другая возможность наблюдения гравитационного линзирования черной дырой — наблюдение за звездами, вращающимися вокруг черной дыры. Есть несколько кандидатов на такое наблюдение на орбите вокруг Стрельца A* . [202]
Альтернативы
Доказательства существования звездных черных дыр в значительной степени опираются на существование верхнего предела массы нейтронной звезды. Размер этого предела в значительной степени зависит от предположений, сделанных относительно свойств плотной материи. Новые экзотические фазы материи могут поднять эту границу. [184] Фаза свободных кварков при высокой плотности может допустить существование плотных кварковых звезд, [203] а некоторые суперсимметричные модели предсказывают существование Q звезд . [204] Некоторые расширения стандартной модели постулируют существование преонов как фундаментальных строительных блоков кварков и лептонов , которые гипотетически могли бы образовывать преонные звезды . [205] Эти гипотетические модели потенциально могли бы объяснить ряд наблюдений кандидатов в звездные черные дыры. Однако из аргументов общей теории относительности можно показать, что любой такой объект будет иметь максимальную массу. [184]
Поскольку средняя плотность черной дыры внутри ее радиуса Шварцшильда обратно пропорциональна квадрату ее массы, сверхмассивные черные дыры гораздо менее плотны, чем звездные черные дыры. Средняя плотность 108 M ☉ черная дыра сравнима с водой. [184] Следовательно, физика материи, образующей сверхмассивную черную дыру, гораздо лучше понята, а возможные альтернативные объяснения наблюдений сверхмассивных черных дыр гораздо более приземленны. Например, сверхмассивная черная дыра может быть смоделирована большим скоплением очень темных объектов. Однако такие альтернативы, как правило, недостаточно стабильны, чтобы объяснить кандидатов в сверхмассивные черные дыры. [184]
Доказательства существования звездных и сверхмассивных черных дыр подразумевают, что для того, чтобы черные дыры не образовывались, общая теория относительности должна потерпеть неудачу как теория гравитации, возможно, из-за появления квантово-механических поправок. Долгожданная особенность теории квантовой гравитации заключается в том, что она не будет содержать сингулярностей или горизонтов событий, и, таким образом, черные дыры не будут реальными артефактами. [206] Например, в модели fuzzball [207], основанной на теории струн , отдельные состояния решения черной дыры, как правило, не имеют горизонта событий или сингулярности, но для классического/полуклассического наблюдателя статистическое среднее таких состояний выглядит так же, как и обычная черная дыра, выведенная из общей теории относительности. [208]
Было высказано предположение, что несколько теоретических объектов соответствуют наблюдениям астрономических кандидатов в черные дыры идентично или почти идентично, [173], но которые функционируют через другой механизм. К ним относятся гравастар , [209] черная звезда , [210] связанный нестар [211] и звезда темной энергии . [212]
Открытые вопросы
Энтропия и термодинамика
В 1971 году Хокинг показал при общих условиях [Примечание 5] , что общая площадь горизонтов событий любой совокупности классических черных дыр никогда не может уменьшиться, даже если они сталкиваются и сливаются. [213] Этот результат, теперь известный как второй закон механики черных дыр , удивительно похож на второй закон термодинамики , который гласит, что полная энтропия изолированной системы никогда не может уменьшиться. Как и в случае с классическими объектами при абсолютной нулевой температуре, предполагалось, что черные дыры имеют нулевую энтропию. Если бы это было так, второй закон термодинамики был бы нарушен материей, нагруженной энтропией, входящей в черную дыру, что привело бы к уменьшению общей энтропии Вселенной. Поэтому Бекенштейн предположил, что черная дыра должна иметь энтропию, и что она должна быть пропорциональна ее площади горизонта. [214]
Связь с законами термодинамики была еще больше укреплена открытием Хокинга в 1974 году, что квантовая теория поля предсказывает, что черная дыра излучает излучение черного тела при постоянной температуре. Это, по-видимому, вызывает нарушение второго закона механики черных дыр, поскольку излучение будет уносить энергию из черной дыры, заставляя ее сжиматься. Излучение также уносит энтропию, и можно доказать при общих предположениях, что сумма энтропии материи, окружающей черную дыру, и одной четверти площади горизонта, измеренной в планковских единицах, на самом деле всегда увеличивается. Это позволяет сформулировать первый закон механики черных дыр как аналог первого закона термодинамики , где масса действует как энергия, поверхностная гравитация как температура, а площадь как энтропия. [214]
Одной из загадочных особенностей является то, что энтропия черной дыры масштабируется с ее площадью, а не с ее объемом, поскольку энтропия обычно является обширной величиной , которая масштабируется линейно с объемом системы. Это странное свойство привело Джерарда 'т Хоофта и Леонарда Сасскинда к предложению голографического принципа , который предполагает, что все, что происходит в объеме пространства-времени, может быть описано данными на границе этого объема. [215]
Хотя общая теория относительности может быть использована для выполнения полуклассического расчета энтропии черной дыры, эта ситуация теоретически неудовлетворительна. В статистической механике энтропия понимается как подсчет числа микроскопических конфигураций системы, которые имеют те же макроскопические качества, такие как масса, заряд, давление и т. д. Без удовлетворительной теории квантовой гравитации невозможно выполнить такое вычисление для черных дыр. Некоторый прогресс был достигнут в различных подходах к квантовой гравитации. В 1995 году Эндрю Стромингер и Кумрун Вафа показали, что подсчет микросостояний конкретной суперсимметричной черной дыры в теории струн воспроизводит энтропию Бекенштейна–Хокинга. [216] С тех пор аналогичные результаты были получены для различных черных дыр как в теории струн, так и в других подходах к квантовой гравитации, таких как петлевая квантовая гравитация . [217]
Парадокс потери информации
Поскольку черная дыра имеет только несколько внутренних параметров, большая часть информации о материи, которая пошла на формирование черной дыры, теряется. Независимо от типа материи, которая попадает в черную дыру, кажется, что сохраняется только информация, касающаяся полной массы, заряда и углового момента. Пока считалось, что черные дыры сохраняются вечно, эта потеря информации не является такой уж проблематичной, поскольку информацию можно считать существующей внутри черной дыры, недоступной извне, но представленной на горизонте событий в соответствии с голографическим принципом. Однако черные дыры медленно испаряются, испуская излучение Хокинга. Это излучение, по-видимому, не несет никакой дополнительной информации о материи, которая образовала черную дыру, а это означает, что эта информация, по-видимому, исчезла навсегда. [218]
Вопрос о том, действительно ли теряется информация в черных дырах ( парадокс информации о черных дырах ), разделил сообщество теоретиков-физиков. В квантовой механике потеря информации соответствует нарушению свойства, называемого унитарностью , и утверждалось, что потеря унитарности также подразумевает нарушение закона сохранения энергии, [219] хотя это также оспаривалось. [220] За последние годы накопилось доказательство того, что информация и унитарность действительно сохраняются в полном квантово-гравитационном подходе к проблеме. [221]
Одна из попыток разрешить информационный парадокс черной дыры известна как дополнительность черной дыры . В 2012 году был введен « парадокс файрвола » с целью продемонстрировать, что дополнительность черной дыры не решает информационный парадокс. Согласно квантовой теории поля в искривленном пространстве-времени , единичное излучение излучения Хокинга включает две взаимно запутанные частицы. Исходящая частица вырывается и испускается как квант излучения Хокинга; падающая частица поглощается черной дырой. Предположим, что черная дыра образовалась конечное время в прошлом и полностью испарится за некоторое конечное время в будущем. Затем она испустит только конечное количество информации, закодированной в ее излучении Хокинга. Согласно исследованиям таких физиков, как Дон Пейдж [222] [223] и Леонард Сасскинд, в конечном итоге наступит время, к которому исходящая частица должна быть запутана со всем излучением Хокинга, которое черная дыра ранее испустила.
Это, по-видимому, создает парадокс: принцип, называемый « моногамией запутанности », требует, чтобы, как и любая квантовая система, исходящая частица не могла быть полностью запутана с двумя другими системами одновременно; однако здесь исходящая частица, по-видимому, запутана как с падающей частицей, так и, независимо, с прошлым излучением Хокинга. [224] Чтобы разрешить это противоречие, физики в конечном итоге могут быть вынуждены отказаться от одного из трех проверенных временем принципов: принципа эквивалентности Эйнштейна, унитарности или локальной квантовой теории поля. Одно из возможных решений, которое нарушает принцип эквивалентности, заключается в том, что «брандмауэр» уничтожает входящие частицы на горизонте событий. [225] В общем, то, от какого из этих предположений — если таковое имеется — следует отказаться, остается предметом споров. [220]
В научной фантастике
Научно-фантастический эпос Кристофера Нолана 2014 года «Интерстеллар» рассказывает о черной дыре, известной как Гаргантюа, которая является центральным объектом планетарной системы в далекой галактике. Человечество получило доступ к этой системе через червоточину во внешней солнечной системе , около Сатурна .
Смотрите также
- Черная брана или Черная струна
- Инициатива «Черная дыра»
- Черная дыра звездолет
- Черные дыры в художественной литературе
- Бланет
- Черная дыра БТЗ
- Золотой двоичный
- Гипотетическая черная дыра (значения)
- Кугельблитц (астрофизика)
- Список черных дыр
- Список ближайших черных дыр
- Схема черных дыр
- Звуковая черная дыра
- Виртуальная черная дыра
- Битва Сасскинда-Хокинга
- Хронология физики черных дыр
- Белая дыра
- звезда Планка
- Темная звезда (темная материя)
Примечания
- ^ Значение cJ/GM 2 может превышать 1 для объектов, отличных от черных дыр. Наибольшее значение, известное для нейтронной звезды, составляет ≤ 0,4, и обычно используемые уравнения состояния ограничивают это значение значением < 0,7. [78]
- ^ Радиус (внешнего) горизонта событий масштабируется как:
- ^ Множество возможных путей, или, точнее, будущий световой конус , содержащий все возможные мировые линии (на этой диаграмме световой конус представлен V-образной областью, ограниченной стрелками, представляющими мировые линии световых лучей), наклонено таким образом в координатах Эддингтона–Финкельштейна (диаграмма представляет собой «мультяшную» версию координатной диаграммы Эддингтона–Финкельштейна), но в других координатах световые конусы не наклонены таким образом, например, в координатах Шварцшильда они сужаются без наклона по мере приближения к горизонту событий, а в координатах Крускала–Шекереша световые конусы вообще не меняют форму или ориентацию. [81]
- ^ Это справедливо только для четырехмерного пространства-времени. В более высоких измерениях возможны более сложные топологии горизонта, такие как черное кольцо . [93] [94]
- ^ В частности, он предположил, что вся материя удовлетворяет слабому энергетическому условию .
Ссылки
- ^ Oldham, LJ; Auger, MW (март 2016 г.). «Структура галактики по множественным трассерам – II. M87 от парсека до мегапарсека». Monthly Notices of the Royal Astronomical Society . 457 (1): 421–439. arXiv : 1601.01323 . Bibcode : 2016MNRAS.457..421O. doi : 10.1093/mnras/stv2982 . ISSN 0035-8711. S2CID 119166670.
- ^ Вальд 1984, стр. 299–300
- ^ ab Wald, RM (1997). «Гравитационный коллапс и космическая цензура». В Iyer, BR; Bhawal, B. (ред.). Черные дыры, гравитационное излучение и Вселенная . Dordrecht: Springer. стр. 69–86. arXiv : gr-qc/9710068 . doi :10.1007/978-94-017-0934-7. ISBN 978-9401709347.
- ↑ Overbye, Dennis (8 июня 2015 г.). «Охотники за черными дырами». NASA . Архивировано из оригинала 9 июня 2015 г. Получено 8 июня 2015 г.
- ^ Гамильтон, А. «Путешествие в черную дыру Шварцшильда». jila.colorado.edu . Архивировано из оригинала 3 сентября 2019 года . Получено 28 июня 2020 года .
- ^ Шутц, Бернард Ф. (2003). Гравитация с самого начала. Cambridge University Press . стр. 110. ISBN 978-0-521-45506-0. Архивировано из оригинала 2 декабря 2016 года.
- ^ Davies, PCW (1978). "Thermodynamics of Black Holes" (PDF) . Reports on Progress in Physics . 41 (8): 1313–1355. Bibcode :1978RPPh...41.1313D. doi :10.1088/0034-4885/41/8/004. S2CID 250916407. Архивировано из оригинала (PDF) 10 мая 2013 г.
- ^ abc Монтгомери, Колин; Орчистон, Уэйн; Уиттингем, Ян (2009). «Мишель, Лаплас и происхождение концепции черной дыры» (PDF) . Журнал астрономической истории и наследия . 12 (2): 90–96. Bibcode :2009JAHH...12...90M. doi :10.3724/SP.J.1440-2807.2009.02.01. S2CID 55890996.
- ^ Вебстер, Б. Луиз; Мурдин, Пол (1972), «Cygnus X-1 — спектроскопическая двойная звезда с тяжелым компаньоном?», Nature , 235 (5332): 37–38, Bibcode : 1972Natur.235...37W, doi : 10.1038/235037a0, S2CID 4195462
- ^ Болтон, CT (1972), «Идентификация Cygnus X-1 с HDE 226868», Nature , 235 (5336): 271–273, Bibcode : 1972Natur.235..271B, doi : 10.1038/235271b0, S2CID 4222070
- ^ Клери Д (2020). «Черные дыры, пойманные в процессе поглощения звезд». Science . 367 (6477): 495. Bibcode :2020Sci...367..495C. doi :10.1126/science.367.6477.495. PMID 32001633. S2CID 210984462.
- ^ Мичелл, Дж. (1784). «О способах обнаружения расстояния, величины и т. д. неподвижных звезд вследствие уменьшения скорости их света в случае, если такое уменьшение будет обнаружено в любой из них, и такие другие данные должны быть получены из наблюдений, которые будут далее необходимы для этой цели». Philosophical Transactions of the Royal Society . 74 : 35–57. Bibcode : 1784RSPT...74...35M. doi : 10.1098/rstl.1784.0008 . JSTOR 106576.
- ^ ab Thorne 1994, стр. 123–124
- ^ Слейтер, Элизабет М.; Слейтер, Генри С. (1992). Световая и электронная микроскопия. Cambridge University Press . ISBN 978-0-521-33948-3. Архивировано из оригинала 30 ноября 2017 года.
- ^ Crass, Institute of Astronomy – Design by DR Wilkins and SJ "Light escaping from black holes". www.ast.cam.ac.uk . Архивировано из оригинала 6 июля 2019 г. . Получено 10 марта 2018 г. .
- ^ Леви, Адам (11 января 2021 г.). «Как черные дыры превратились из теории в реальность». Knowable Magazine . doi : 10.1146/knowable-010921-1 . Получено 25 марта 2022 г. .
- ^ аб Шварцшильд, К. (1916). «Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 7 : 189–196. Бибкод : 1916SPAW.......189S.
- Перевод: Antoci, S.; Loinger, A. (1999). «О гравитационном поле материальной точки согласно теории Эйнштейна». arXiv : physics/9905030 .и Шварцшильд, К. (1916). «Über das Gravitationsfeld einer Kugel aus incompressibler Flüssigkeit nach der Einsteinschen Theorie». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 18 : 424–434. Бибкод : 1916skpa.conf..424S.
- Перевод: Antoci, S. (1999). «О гравитационном поле сферы несжимаемой жидкости согласно теории Эйнштейна». arXiv : physics/9912033 .
- ^ Droste, J. (1917). «О поле одного центра в теории гравитации Эйнштейна и движении частицы в этом поле» (PDF) . Труды Королевской академии Амстердама . 19 (1): 197–215. Архивировано из оригинала (PDF) 18 мая 2013 г. . Получено 16 сентября 2012 г. .
- ^ Kox, AJ (1992). "Общая теория относительности в Нидерландах: 1915–1920". В Eisenstaedt, Jean; Kox, AJ (ред.). Исследования по истории общей теории относительности . Birkhäuser. стр. 41. ISBN 978-0-8176-3479-7. Архивировано из оригинала 10 августа 2016 . Получено 23 февраля 2016 .
- ^ 't Hooft, G. (2009). "Введение в теорию черных дыр" (PDF) . Институт теоретической физики / Институт Спинозы. стр. 47–48. Архивировано из оригинала (PDF) 21 мая 2009 г. . Получено 24 июня 2010 г. .
- ^ Эддингтон, Артур (1926). Внутреннее строение звезд. Science. Vol. 52. Cambridge University Press. pp. 233–40. Bibcode : 1920Sci....52..233E. doi : 10.1126/science.52.1341.233. ISBN 978-0-521-33708-3. PMID 17747682. Архивировано из оригинала 11 августа 2016 г.
- ^ Торн, Кип С.; Хокинг, Стивен (1994). Черные дыры и искривления времени: возмутительное наследие Эйнштейна . WW Norton & Company. стр. 134–135. ISBN 978-0-393-31276-8. Получено 12 апреля 2019 г. .
Первым выводом была ньютоновская версия света, не выходящего наружу; вторым было полуточное, релятивистское описание; а третьим была типичная гипербола Эддингтона ... когда звезда столь же мала, как критическая окружность, кривизна сильна, но не бесконечна, и пространство определенно не обернуто вокруг звезды. Эддингтон, возможно, знал это, но его описание стало хорошей историей, и оно причудливым образом уловило дух кривизны пространства-времени Шварцшильда.
- ^ Венкатараман, Г. (1992). Чандрасекар и его предел. Universities Press. стр. 89. ISBN 978-81-7371-035-3. Архивировано из оригинала 11 августа 2016 года.
- ^ Детвейлер, С. (1981). «Ресурсное письмо BH-1: Черные дыры». American Journal of Physics . 49 (5): 394–400. Bibcode : 1981AmJPh..49..394D. doi : 10.1119/1.12686.
- ^ Харпас, А. (1994). Звездная эволюция. АК Петерс . п. 105. ИСБН 978-1-56881-012-6. Архивировано из оригинала 11 августа 2016 года.
- ^ ab Оппенгеймер, Дж. Р.; Волков , Г. М. (1939). «О массивных нейтронных ядрах». Physical Review . 55 (4): 374–381. Bibcode : 1939PhRv...55..374O. doi : 10.1103/PhysRev.55.374.
- ^ Бомбачи, И. (1996). «Максимальная масса нейтронной звезды». Астрономия и астрофизика . 305 : 871–877. Bibcode : 1996A&A...305..871B.
- ^ Чо, А. (16 февраля 2018 г.). «Ограничение веса нейтронных звезд». Science . 359 (6377): 724–725. Bibcode :2018Sci...359..724C. doi :10.1126/science.359.6377.724. PMID 29449468.
- ^ Маргалит, Б.; Мецгер, Б.Д. (1 декабря 2017 г.). «Ограничение максимальной массы нейтронных звезд по многоканальным наблюдениям GW170817». The Astrophysical Journal . 850 (2): L19. arXiv : 1710.05938 . Bibcode :2017ApJ...850L..19M. doi : 10.3847/2041-8213/aa991c . S2CID 119342447.
- ^ Шибата, М.; Фудзибаяси, С.; Хотокезака, К.; Киучи, К.; Кьютоку, К.; Секигучи, Й.; Танака, М. (22 декабря 2017 г.). «Моделирование GW170817 на основе численной теории относительности и его последствия». Physical Review D. 96 ( 12): 123012. arXiv : 1710.07579 . Bibcode : 2017PhRvD..96l3012S. doi : 10.1103/PhysRevD.96.123012. S2CID 119206732.
- ^ Руис, М.; Шапиро, С.Л.; Цокарос, А. (11 января 2018 г.). «GW170817, общее релятивистское магнитогидродинамическое моделирование и максимальная масса нейтронной звезды». Physical Review D. 97 ( 2): 021501. arXiv : 1711.00473 . Bibcode : 2018PhRvD..97b1501R. doi : 10.1103 / PhysRevD.97.021501. PMC 6036631. PMID 30003183.
- ^ Rezzolla, L.; Most, ER; Weih, LR (9 января 2018 г.). «Использование наблюдений гравитационных волн и квазиуниверсальных отношений для ограничения максимальной массы нейтронных звезд». Astrophysical Journal . 852 (2): L25. arXiv : 1711.00314 . Bibcode :2018ApJ...852L..25R. doi : 10.3847/2041-8213/aaa401 . S2CID 119359694.
- ^ Ruffini, R. ; Wheeler, JA (1971). "Introducing the black hole" (PDF) . Physics Today . 24 (1): 30–41. Bibcode :1971PhT....24a..30R. doi :10.1063/1.3022513. Архивировано из оригинала (PDF) 25 июля 2011 г. . Получено 5 декабря 2009 г. .
- ^ ab Бернстайн, Джереми (2007). «Неохотный отец черных дыр». Scientific American . 17 : 4–11. doi :10.1038/scientificamerican0407-4sp . Получено 3 августа 2023 г.
- ^ Оппенгеймер, Дж. Р.; Снайдер, Х. (1939). «О продолжении гравитационного сжатия». Physical Review . 56 (5): 455–459. Bibcode :1939PhRv...56..455O. doi : 10.1103/PhysRev.56.455 .
- ^ Финкельштейн, Д. (1958). «Прошлое-будущее асимметрия гравитационного поля точечной частицы». Physical Review . 110 (4): 965–967. Bibcode : 1958PhRv..110..965F. doi : 10.1103/PhysRev.110.965.
- ^ Крускал, М. (1960). «Максимальное расширение метрики Шварцшильда». Physical Review . 119 (5): 1743. Bibcode : 1960PhRv..119.1743K. doi : 10.1103/PhysRev.119.1743.
- ^ Хьюиш, А. и др. (1968). «Наблюдение быстро пульсирующего радиоисточника». Nature . 217 (5130): 709–713. Bibcode :1968Natur.217..709H. doi :10.1038/217709a0. S2CID 4277613.
- ^ Pilkington, JDH; et al. (1968). «Наблюдения некоторых дополнительных источников импульсного радиоизлучения». Nature . 218 (5137): 126–129. Bibcode :1968Natur.218..126P. doi :10.1038/218126a0. S2CID 4253103.
- ^ Хьюиш, А. (1970). «Пульсары». Annual Review of Astronomy and Astrophysics . 8 (1): 265–296. Bibcode : 1970ARA&A...8..265H. doi : 10.1146/annurev.aa.08.090170.001405.
- ^ Буассоно, Лотарингия (28 февраля 2018 г.). «Пятьдесят лет назад открытие аспиранта изменило курс астрофизики». Smithsonian Magazine . Получено 22 декабря 2023 г. .
- ^ Ньюман, ET ; и др. (1965). «Метрика вращающейся заряженной массы». Журнал математической физики . 6 (6): 918. Bibcode : 1965JMP.....6..918N. doi : 10.1063/1.1704351.
- ^ Israel, W. (1967). «Горизонты событий в статическом вакуумном пространстве-времени». Physical Review . 164 (5): 1776. Bibcode : 1967PhRv..164.1776I. doi : 10.1103/PhysRev.164.1776.
- ^ Картер, Б. (1971). «Осесимметричная черная дыра имеет только две степени свободы». Physical Review Letters . 26 (6): 331. Bibcode : 1971PhRvL..26..331C. doi : 10.1103/PhysRevLett.26.331.
- ^ Картер, Б. (1977). «Теорема об уникальности вакуумной черной дыры и ее возможные обобщения». Труды 1-го совещания Марселя Гроссмана по общей теории относительности . С. 243–254.
- ^ Робинсон, Д. (1975). «Уникальность черной дыры Керра». Physical Review Letters . 34 (14): 905. Bibcode : 1975PhRvL..34..905R. doi : 10.1103/PhysRevLett.34.905.
- ^ ab Heusler, M. (2012). "Stationary Black Holes: Uniqueness and Beyond". Living Reviews in Relativity . 15 (7): 7. arXiv : 1205.6112 . Bibcode : 2012LRR ....15....7C. doi : 10.12942/lrr-2012-7 . PMC 5255892. PMID 28179837.
- ^ ab Penrose, R. (1965). "Gravitational Collapse and Space-Time Singularities" (PDF) . Physical Review Letters . 14 (3): 57. Bibcode :1965PhRvL..14...57P. doi :10.1103/PhysRevLett.14.57. S2CID 116755736. Архивировано из оригинала (PDF) 11 октября 2020 г.
- ^ Ford, LH (2003). «Классические теоремы о сингулярности и их квантовые лазейки». International Journal of Theoretical Physics . 42 (6): 1219–1227. arXiv : gr-qc/0301045 . Bibcode :2003gr.qc.....1045F. doi :10.1023/A:1025754515197. S2CID 14404560.
- ^ "Нобелевская премия по физике 2020 года". NobelPrize.org . Архивировано из оригинала 24 апреля 2021 года . Получено 8 октября 2020 года .
- ↑ Ролстон, Брюс (10 ноября 1997 г.), Первая черная дыра, Университет Торонто, архивировано из оригинала 7 марта 2008 г. , извлечено 11 марта 2008 г.
- ^ Шипман, HL; Ю, Z; Ду, YW (1975), «Неправдоподобная история моделей тройных звезд для Лебедя X-1. Свидетельство черной дыры», Astrophysical Letters , 16 (1): 9–12, Bibcode : 1975ApL....16....9S, doi : 10.1016/S0304-8853(99)00384-4
- ^ Bardeen, JM ; Carter, B. ; Hawking, SW (1973). "Четыре закона механики черных дыр". Communications in Mathematical Physics . 31 (2): 161–170. Bibcode :1973CMaPh..31..161B. doi :10.1007/BF01645742. MR 0334798. S2CID 54690354. Zbl 1125.83309. Архивировано из оригинала 16 мая 2020 г. Получено 4 июня 2021 г.
- ^ abc Хокинг, SW (1974). «Взрывы черных дыр?». Nature . 248 (5443): 30–31. Bibcode : 1974Natur.248...30H. doi : 10.1038/248030a0. S2CID 4290107.
- ^ abcd Эбботт, BP; и др. (2016). "Наблюдение гравитационных волн от слияния бинарных черных дыр". Phys. Rev. Lett. 116 (6): 061102. arXiv : 1602.03837 . Bibcode :2016PhRvL.116f1102A. doi :10.1103/PhysRevLett.116.061102. PMID 26918975. S2CID 124959784.
- ^ Event Horizon Telescope, The (2019). "Результаты первого телескопа M87 Event Horizon. I. Тень сверхмассивной черной дыры". The Astrophysical Journal . 875 (1): L1. arXiv : 1906.11238 . Bibcode : 2019ApJ...875L...1E. doi : 10.3847/2041-8213/ab0ec7 . S2CID 145906806.
- ^ Боуман, Кэтрин Л .; Джонсон, Майкл Д.; Зоран, Дэниел; Фиш, Винсент Л.; Доулман, Шеперд С.; Фримен, Уильям Т. (2016). «Вычислительная визуализация для реконструкции изображений VLBI». Конференция IEEE 2016 года по компьютерному зрению и распознаванию образов (CVPR) . стр. 913–922. arXiv : 1512.01413 . doi : 10.1109/CVPR.2016.105. hdl : 1721.1/103077. ISBN 978-1-4673-8851-1. S2CID 9085016.
- ^ Гардинер, Эйдан (12 апреля 2018 г.). «Когда черная дыра наконец-то раскрывает себя, нам очень помогает наш собственный космический репортер — в среду астрономы объявили, что им удалось сделать первое изображение черной дыры. Деннис Овербай из The Times отвечает на вопросы читателей». The New York Times . Архивировано из оригинала 1 января 2022 г. . Получено 15 апреля 2019 г. .
- ^ Эль-Бадри, Карим; Рикс, Ханс-Вальтер; Кватерт, Элиот; Говард, Эндрю В.; Айзексон, Говард; Фуллер, Джим; Хокинс, Кит; Брейвик, Кейтлин; Вонг, Казе В.К.; Родригес, Антонио К.; Конрой, Чарли; Шахаф, Сахар; Мазех, Цеви; Арену, Фредерик; Бердж, Кевин Б.; Баши, Долев; Файглер, Симхон; Вайс, Дэниел Р.; Сибургер, Рис; Монтер, Сильвия Альмада; Войно, Дженнифер (2023). «Звезда, похожая на Солнце, вращается вокруг черной дыры». Monthly Notices of the Royal Astronomical Society . 518 : 1057–1085. arXiv : 2209.06833 . doi : 10.1093/mnras/stac3140 .
- ^ "ESO Instrument Finds Closest Black Hole to Earth". Европейская южная обсерватория . 6 мая 2020 г. Архивировано из оригинала 6 мая 2020 г. Получено 2 апреля 2021 г.
- ^ ab "Марсия Бартусяк из Массачусетского технологического института о понимании нашего места во Вселенной". www.wbur.org . 9 октября 2018 г. Архивировано из оригинала 12 апреля 2019 г. Получено 12 апреля 2019 г.
- ^ ab Siegfried, Tom (23 декабря 2013 г.). "50 лет спустя трудно сказать, кто дал название черным дырам". Science News . Архивировано из оригинала 9 марта 2017 г. . Получено 24 сентября 2017 г. Похоже
, что ярлык "черная дыра" также обсуждался в январе 1964 г. в Кливленде на встрече Американской ассоциации содействия развитию науки. Репортер Science News Letter Энн Юинг сделала репортаж с той встречи, описав, как интенсивное гравитационное поле может заставить звезду схлопнуться сама в себя. "Затем такая звезда образует "черную дыру" во Вселенной", - написала Юинг
- ↑ Браун, Эмма (3 августа 2010 г.). «Энн Э. Юинг, журналистка, первая сообщила о черных дырах». Boston.com . Архивировано из оригинала 24 сентября 2017 г. Получено 24 сентября 2017 г.
- ^ "Pioneering Physicist John Wheeler Dies at 96". Scientific American . Архивировано из оригинала 28 ноября 2016 года . Получено 27 ноября 2016 года .
- ↑ Overbye, Dennis (14 апреля 2008 г.). «Джон А. Уилер, физик, придумавший термин «черная дыра», умер в возрасте 96 лет». The New York Times . Архивировано из оригинала 22 ноября 2016 г. Получено 27 ноября 2016 г.
- ^ Кэрролл 2004, стр. 253
- ^ Рейнольдс, Кристофер С. (январь 2019 г.). «Наблюдение вращения черных дыр». Nature Astronomy . 3 (1): 41–47. arXiv : 1903.11704 . Bibcode :2019NatAs...3...41R. doi :10.1038/s41550-018-0665-z. ISSN 2397-3366. S2CID 85543351. Архивировано из оригинала 18 ноября 2020 г. . Получено 21 августа 2020 г. .
- ^ Торн, К. С .; Прайс, Р. Х. (1986). Черные дыры: мембранная парадигма . Издательство Йельского университета. ISBN 978-0-300-03770-8.
- ^ ab Anderson, Warren G. (1996). "Проблема потери информации в черной дыре". Usenet Physics FAQ . Архивировано из оригинала 22 января 2009 года . Получено 24 марта 2009 года .
- ^ Preskill, J. (21 октября 1994 г.). Черные дыры и информация: кризис в квантовой физике (PDF) . Caltech Theory Seminar. Архивировано из оригинала (PDF) 18 мая 2008 г. . Получено 17 мая 2009 г. .
- ^ Preskill, J. (21 октября 1994 г.). Черные дыры и информация: кризис в квантовой физике (PDF) . Caltech Theory Seminar. Архивировано из оригинала (PDF) 18 мая 2008 г. . Получено 17 мая 2009 г. .
- ^ Хокинг и Эллис 1973, Приложение B
- ^ Сидс, Майкл А.; Бэкман, Дана Э. (2007). Перспективы астрономии. Cengage Learning. стр. 167. ISBN 978-0-495-11352-2. Архивировано из оригинала 10 августа 2016 года.
- ^ Шапиро, С. Л.; Тьюкольский, С. А. (1983). Черные дыры, белые карлики и нейтронные звезды: физика компактных объектов . John Wiley and Sons. стр. 357. ISBN 978-0-471-87316-7.
- ^ Бергер, Б. К. (2002). «Численные подходы к сингулярностям пространства-времени». Living Reviews in Relativity . 5 (1): 2002–1. arXiv : gr-qc/0201056 . Bibcode : 2002LRR.....5....1B. doi : 10.12942/lrr-2002-1 . PMC 5256073. PMID 28179859 .
- ^ МакКлинток, Дж. Э.; Шафи, Р.; Нараян, Р.; Ремиллард, РА; Дэвис, С. В.; Ли, Л.-Х. (2006). «Вращение почти экстремальной черной дыры Керра GRS 1915+105». Astrophysical Journal . 652 (1): 518–539. arXiv : astro-ph/0606076 . Bibcode :2006ApJ...652..518M. doi :10.1086/508457. S2CID 1762307.
- ^ abc Abbott, BP; et al. ( LIGO Scientific Collaboration и Virgo Collaboration ) (1 июня 2017 г.). "GW170104: Наблюдение за слиянием двойной черной дыры массой 50 солнечных при красном смещении 0,2". Physical Review Letters . 118 (22): 221101. arXiv : 1706.01812 . Bibcode : 2017PhRvL.118v1101A. doi : 10.1103/PhysRevLett.118.221101. PMID 28621973. S2CID 206291714.
- ^ Эбботт, Б. П. и др. ( LIGO Scientific Collaboration & Virgo Collaboration ) (16 октября 2017 г.). "GW170817: Наблюдение гравитационных волн от двойной нейтронной звезды Inspiral". Physical Review Letters . 119 (16): 161101. arXiv : 1710.05832 . Bibcode : 2017PhRvL.119p1101A. doi : 10.1103/PhysRevLett.119.161101. PMID 29099225. S2CID 217163611.
- ^ Вальд 1984, стр. 124–125
- ^ Saa, Alberto; Santarelli, Raphael (18 июля 2011 г.). «Уничтожение почти экстремальной черной дыры Керра–Ньюмена». Physical Review D. 84 ( 2): 027501. arXiv : 1105.3950 . Bibcode : 2011PhRvD..84b7501S. doi : 10.1103/PhysRevD.84.027501. S2CID 118487989.
- ^ Мизнер, Торн и Уилер 1973, стр. 848
- ^ Дэвис, Пол (1992). Новая физика (иллюстрированное издание). Cambridge University Press. стр. 26. ISBN 978-0-521-43831-5. Архивировано из оригинала 17 августа 2021 . Получено 25 сентября 2020 .Выдержка из страницы 26 Архивировано 15 августа 2021 г. на Wayback Machine
- ^ Флейш, Дэниел; Крегенов, Джулия (2013). Руководство для студентов по математике астрономии (иллюстрированное издание). Cambridge University Press. стр. 168. ISBN 978-1-107-03494-5. Архивировано из оригинала 17 августа 2021 . Получено 25 сентября 2020 .Выдержка из страницы 168 Архивировано 17 августа 2021 г. на Wayback Machine
- ^ Уиллер 2007, стр. 179
- ^ Кэрролл 2004, гл. 5.4 и 7.3
- ^ "Сингулярности и черные дыры > Световые конусы и причинная структура". plato.stanford.edu . Стэнфордская энциклопедия философии . Архивировано из оригинала 17 мая 2019 года . Получено 11 марта 2018 года .
- ^ Кэрролл 2004, стр. 217
- ^ Кэрролл 2004, стр. 218
- ^ "Внутри черной дыры". Познание вселенной и ее секретов . Архивировано из оригинала 23 апреля 2009 года . Получено 26 марта 2009 года .
- ^ "Что случится с вами, если вы упадете в черную дыру". math.ucr.edu . Джон Баез . Архивировано из оригинала 13 февраля 2019 года . Получено 11 марта 2018 года .
- ^ Кэрролл 2004, стр. 222
- ^ "Watch: Three Ways a Astronaut Could Fall Into a Black Hole". 1 февраля 2014 г. Архивировано из оригинала 15 апреля 2019 г. Получено 13 марта 2018 г.
- ^ Эмпаран, Р.; Реалл, Х.С. (2008). «Черные дыры в высших измерениях». Living Reviews in Relativity . 11 (6): 6. arXiv : 0801.3471 . Bibcode : 2008LRR....11....6E. doi : 10.12942/lrr-2008-6 . PMC 5253845. PMID 28163607 .
- ^ Obers, NA (2009). Papantonopoulos, Eleftherios (ред.). Physics of Black Holes (PDF) . Lecture Notes in Physics. Vol. 769. Berlin, Heidelberg. pp. 211–258. arXiv : 0802.0519 . Bibcode :2009LNP...769.....P. doi :10.1007/978-3-540-88460-6. ISBN 978-3-540-88459-0. Архивировано (PDF) из оригинала 26 июля 2018 г. . Получено 27 июля 2018 г. .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Хокинг и Эллис 1973, Гл. 9.3
- ^ Смарр, Л. (1973). «Поверхностная геометрия заряженных вращающихся черных дыр». Physical Review D. 7 ( 2): 289–295. Bibcode :1973PhRvD...7..289S. doi :10.1103/PhysRevD.7.289.
- ^ Visser, M. (22 января 2009 г.). "Пространство-время Керра: краткое введение". В Wiltshire, DL; Visser, M.; Scott, SM (ред.). Пространство-время Керра: вращающиеся черные дыры в общей теории относительности. Cambridge University Press. arXiv : 0706.0622 . ISBN 978-052188512-6. Архивировано из оригинала 20 мая 2020 . Получено 12 января 2020 .
- ^ Delgado, JFM; Herdeiro, CAR; Radu, E. (2018). «Геометрия горизонта для черных дыр Керра с синхронизированными волосами». Physical Review D. 97 ( 12): 124012. arXiv : 1804.04910 . Bibcode : 2018PhRvD..97l4012D. doi : 10.1103/PhysRevD.97.124012. hdl : 10773/24121. S2CID 55732213.
- ^ Кэрролл 2004, стр. 205
- ^ Кэрролл 2004, стр. 264–265
- ^ Кэрролл 2004, стр. 252
- ^ «Размеры черных дыр? Насколько велика черная дыра?». Sky & Telescope . 22 июля 2014 г. Архивировано из оригинала 3 апреля 2019 г. Получено 9 октября 2018 г.
- ^ Льюис, GF; Кван, J. (2007). «Нет пути назад: максимизация времени выживания ниже горизонта событий Шварцшильда». Публикации Астрономического общества Австралии . 24 (2): 46–52. arXiv : 0705.1029 . Bibcode : 2007PASA...24...46L. doi : 10.1071/AS07012. S2CID 17261076.
- ^ Уиллер 2007, стр. 182
- ↑ Кэрролл 2004, стр. 257–259 и 265–266.
- ^ Droz, S.; Israel, W.; Morsink, SM (1996). «Черные дыры: внутренняя история». Physics World . 9 (1): 34–37. Bibcode : 1996PhyW....9...34D. doi : 10.1088/2058-7058/9/1/26.
- ^ Кэрролл 2004, стр. 266
- ^ Пуассон, Э.; Израэль, В. (1990). «Внутренняя структура черных дыр». Physical Review D. 41 ( 6): 1796–1809. Bibcode : 1990PhRvD..41.1796P. doi : 10.1103/PhysRevD.41.1796. PMID 10012548.
- ^ Вальд 1984, стр. 212
- ^ Хамаде, Р. (1996). «Черные дыры и квантовая гравитация». Кембриджская теория относительности и космология . Кембриджский университет. Архивировано из оригинала 7 апреля 2009 года . Получено 26 марта 2009 года .
- ^ Палмер, Д. «Спросите астрофизика: квантовая гравитация и черные дыры». NASA. Архивировано из оригинала 28 марта 2009 года . Получено 26 марта 2009 года .
- ^ Крамер, Клаес Р. (1997). «Использование незаряженной черной дыры Керра в качестве гравитационного зеркала». Общая теория относительности и гравитация . 29 (4): 445–454. arXiv : gr-qc/9510053 . Bibcode :1997GReGr..29..445C. doi :10.1023/A:1018878515046. S2CID 9517046.
- ^ ab Nitta, Daisuke; Chiba, Takeshi; Sugiyama, Naoshi (сентябрь 2011 г.). "Тени сталкивающихся черных дыр". Physical Review D. 84 ( 6): 063008. arXiv : 1106.2425 . Bibcode : 2011PhRvD..84f3008N. doi : 10.1103/PhysRevD.84.063008. S2CID 119264596.
- ^ Бардин, Джеймс М.; Пресс, Уильям Х.; Тьюкольский, Сол А. (1 декабря 1972 г.). «Вращающиеся черные дыры: локально невращающиеся рамки, извлечение энергии и скалярное синхротронное излучение». The Astrophysical Journal . 178 : 347–370. Bibcode : 1972ApJ...178..347B. doi : 10.1086/151796.
- ^ "Black Hole Calculator". Фабио Пакуччи . Архивировано из оригинала 21 октября 2020 года . Получено 29 сентября 2020 года .
- ^ ab Visser, Matt (2007). "Пространство-время Керра: краткое введение". стр. 35, рис. 3. arXiv : 0706.0622 [gr-qc].
- ^ Кэрролл 2004, Гл. 6.6
- ^ Кэрролл 2004, Гл. 6.7
- ^ Мизнер, Торн и Уилер 1973, Вставка 25.6
- ^ Бардин, Дж. М. (1972). «Вращающиеся черные дыры: локально невращающиеся системы отсчета, извлечение энергии и скалярное синхротронное излучение». The Astrophysical Journal . 178 : 347–370. Bibcode : 1972ApJ...178..347B. doi : 10.1086/151796.
- ^ «Первое доказательство существования «погружающихся областей» черной дыры». Физический факультет. Оксфордский университет . 16 мая 2024 г.
- ^ Маммери, Эндрю; Ингрэм, Адам; Дэвис, Шейн; Фабиан, Эндрю (июнь 2024 г.). «Континуальное излучение из погружающейся области дисков черных дыр». Monthly Notices of the Royal Astronomical Society . 531 (1): 366–386. arXiv : 2405.09175 . doi : 10.1093/mnras/stae1160 .
- ^ Эйнштейн, А. (1939). «О стационарной системе со сферической симметрией, состоящей из многих гравитирующих масс» (PDF) . Annals of Mathematics . 40 (4): 922–936. Bibcode :1939AnMat..40..922E. doi :10.2307/1968902. JSTOR 1968902. S2CID 55495712. Архивировано из оригинала (PDF) 28 февраля 2019 г.
- ^ Керр, РП (2009). «Метрики Керра и Керра-Шилда». В Уилтшире, ДЛ; Виссер, М.; Скотт, СМ (ред.). Пространство-время Керра . Издательство Кембриджского университета. arXiv : 0706.1109 . Bibcode : 2007arXiv0706.1109K. ISBN 978-0-521-88512-6.
- ^ Финдли, Кейт (27 декабря 2019 г.). «Открытие черных дыр: от теории к реальности». Wonderium Daily . Получено 29 июня 2022 г.[ постоянная мертвая ссылка ]
- ^ Хокинг, SW ; Пенроуз, R. (январь 1970). "Сингулярности гравитационного коллапса и космология". Труды Королевского общества A . 314 (1519): 529–548. Bibcode :1970RSPSA.314..529H. doi : 10.1098/rspa.1970.0021 . JSTOR 2416467.
- ^ abc Pacucci, F.; Ferrara, A.; Grazian, A.; Fiore, F.; Giallongo, E. (2016). "Первая идентификация кандидатов в черные дыры с прямым коллапсом в ранней Вселенной в CANDELS/GOODS-S". Mon. Not. R. Astron. Soc . 459 (2): 1432. arXiv : 1603.08522 . Bibcode : 2016MNRAS.459.1432P. doi : 10.1093/mnras/stw725 . S2CID 118578313.
- ^ ab Carr, BJ (2005). «Первичные черные дыры: существуют ли они и полезны ли они?». В Suzuki, H.; Yokoyama, J.; Suto, Y.; Sato, K. (ред.). Раздувающий горизонт астрофизики и космологии частиц . Universal Academy Press. стр. astro–ph/0511743. arXiv : astro-ph/0511743 . Bibcode :2005astro.ph.11743C. ISBN 978-4-946443-94-7.
- ^ "Ripped Apart by a Black Hole". Пресс-релиз ESO . Архивировано из оригинала 21 июля 2013 года . Получено 19 июля 2013 года .
- ^ abc Кэрролл 2004, Раздел 5.8
- ^ abc Rees, MJ; Volonteri, M. (2007). Karas, V.; Matt, G. (ред.). Массивные черные дыры: Формирование и эволюция . Труды Международного астрономического союза. Т. 238. С. 51–58. arXiv : astro-ph/0701512 . Bibcode :2007IAUS..238...51R. doi :10.1017/S1743921307004681. ISBN 978-0-521-86347-6. S2CID 14844338.
{{cite book}}:|journal=проигнорировано ( помощь ) - ^ Bañados, Eduardo; Venemans, Bram P.; Mazzucchelli, Chiara; Farina, Emanuele P.; Walter, Fabian; Wang, Feige; Decarli, Roberto; Stern, Daniel; Fan, Xiaohui; Davies, Frederick B.; Hennawi, Joseph F. (1 января 2018 г.). «Черная дыра массой 800 миллионов солнечных масс в существенно нейтральной Вселенной при красном смещении 7,5». Nature . 553 (7689): 473–476. arXiv : 1712.01860 . Bibcode :2018Natur.553..473B. doi :10.1038/nature25180. PMID 29211709. S2CID 205263326.
- ^ Пенроуз, Р. (2002). "Гравитационный коллапс: роль общей теории относительности" (PDF) . Общая теория относительности и гравитация . 34 (7): 1141. Bibcode :2002GReGr..34.1141P. doi :10.1023/A:1016578408204. S2CID 117459073. Архивировано из оригинала (PDF) 26 мая 2013 г.
- ^ Филип Гиббс. «Является ли Большой взрыв черной дырой?». Джон Баэз . Архивировано из оригинала 31 декабря 2018 года . Получено 16 марта 2018 года .
- ^ Гиддингс, СБ; Томас, С. (2002). «Высокоэнергетические коллайдеры как фабрики черных дыр: конец физики коротких расстояний». Physical Review D. 65 ( 5): 056010. arXiv : hep-ph/0106219 . Bibcode : 2002PhRvD..65e6010G. doi : 10.1103/PhysRevD.65.056010. S2CID 1203487.
- ^ Харада, Т. (2006). «Существует ли минимальная масса черной дыры?». Physical Review D. 74 ( 8): 084004. arXiv : gr-qc/0609055 . Bibcode : 2006PhRvD..74h4004H. doi : 10.1103/PhysRevD.74.084004. S2CID 119375284.
- ^ Arkani–Hamed, N.; Dimopoulos, S.; Dvali, G. (1998). «Проблема иерархии и новые измерения на миллиметре». Physics Letters B. 429 ( 3–4): 263–272. arXiv : hep-ph/9803315 . Bibcode : 1998PhLB..429..263A. doi : 10.1016/S0370-2693(98)00466-3. S2CID 15903444.
- ^ Группа оценки безопасности LHC (2008). "Обзор безопасности столкновений LHC" (PDF) . Журнал физики G: Ядерная физика . 35 (11): 115004. arXiv : 0806.3414 . Bibcode :2008JPhG...35k5004E. doi :10.1088/0954-3899/35/11/115004. S2CID 53370175. Архивировано (PDF) из оригинала 14 апреля 2010 г.
- ^ Кавалья, М. (2010). «Ускорители частиц как фабрики черных дыр?». Einstein-Online . 4 : 1010. Архивировано из оригинала 8 мая 2013 г. Получено 8 мая 2013 г.
- ^ Vesperini, E.; McMillan, SLW; d'Ercole, A.; et al. (2010). "Черные дыры средней массы в ранних шаровых скоплениях". The Astrophysical Journal Letters . 713 (1): L41–L44. arXiv : 1003.3470 . Bibcode : 2010ApJ...713L..41V. doi : 10.1088/2041-8205/713/1/L41. S2CID 119120429.
- ^ Zwart, SFP; Baumgardt, H.; Hut, P.; et al. (2004). «Формирование массивных черных дыр посредством неконтролируемых столкновений в плотных молодых звездных скоплениях». Nature . 428 (6984): 724–726. arXiv : astro-ph/0402622 . Bibcode :2004Natur.428..724P. doi :10.1038/nature02448. PMID 15085124. S2CID 4408378.
- ^ O'Leary, RM; Rasio, FA; Fregeau, JM; et al. (2006). «Двойные слияния и рост черных дыр в плотных звездных скоплениях». The Astrophysical Journal . 637 (2): 937–951. arXiv : astro-ph/0508224 . Bibcode : 2006ApJ...637..937O. doi : 10.1086/498446. S2CID 1509957.
- ^ Page, DN (2005). "Излучение Хокинга и термодинамика черных дыр". New Journal of Physics . 7 (1): 203. arXiv : hep-th/0409024 . Bibcode : 2005NJPh....7..203P. doi : 10.1088/1367-2630/7/1/203. S2CID 119047329.
- ^ Кэрролл 2004, Гл. 9.6
- ^ Siegel, Ethan (2017). «Спросите Ethan: черные дыры растут быстрее, чем испаряются?». Forbes (блог «Starts With A Bang») . Архивировано из оригинала 22 ноября 2018 года . Получено 17 марта 2018 года .
- ^ Sivaram, C. (2001). «Излучение Хокинга черной дыры может никогда не наблюдаться!». Общая теория относительности и гравитация . 33 (2): 175–181. Bibcode : 2001GReGr..33..175S. doi : 10.1023/A:1002753400430. S2CID 118913634.
- ^ "Испаряющиеся черные дыры?". Эйнштейн онлайн . Институт гравитационной физики им. Макса Планка. 2010. Архивировано из оригинала 22 июля 2011 г. Получено 12 декабря 2010 г.
- ^ Гиддингс, СБ; Мангано, МЛ (2008). "Астрофизические последствия гипотетических стабильных черных дыр масштаба ТэВ". Physical Review D. 78 ( 3): 035009. arXiv : 0806.3381 . Bibcode : 2008PhRvD..78c5009G. doi : 10.1103/PhysRevD.78.035009. S2CID 17240525.
- ^ Пескин, М. Э. (2008). «Конец света на Большом адронном коллайдере?». Физика . 1 : 14. Bibcode : 2008PhyOJ...1...14P. doi : 10.1103/Physics.1.14 .
- ^ Fichtel, CE; Bertsch, DL; Dingus, BL ; et al. (1994). «Поиск данных экспериментального телескопа энергетического гамма-излучения (EGRET) для высокоэнергетических микросекундных всплесков гамма-излучения». Astrophysical Journal . 434 (2): 557–559. Bibcode : 1994ApJ...434..557F. doi : 10.1086/174758.
- ^ Naeye, R. "Testing Fundamental Physics". NASA. Архивировано из оригинала 31 августа 2008 года . Получено 16 сентября 2008 года .
- ^ ab Frautschi, S. (1982). «Энтропия в расширяющейся Вселенной». Science . 217 (4560): 593–599. Bibcode :1982Sci...217..593F. doi :10.1126/science.217.4560.593. PMID 17817517. S2CID 27717447.См. страницу 596: таблица 1 и раздел «Распад черной дыры» и предыдущее предложение на этой странице.
- ^ Пейдж, Дон Н. (1976). «Скорость испускания частиц из черной дыры: безмассовые частицы из незаряженной, невращающейся дыры». Physical Review D. 13 ( 2): 198–206. Bibcode : 1976PhRvD..13..198P. doi : 10.1103/PhysRevD.13.198.. См. в частности уравнение (27).
- ^ "Черные дыры | Управление научных миссий". NASA. Архивировано из оригинала 17 ноября 2017 года . Получено 17 марта 2018 года .
- ^ "April 2017 Observations". Event Horizon Telescope . Архивировано из оригинала 10 апреля 2019 года . Получено 11 апреля 2019 года .
- ^ До свидания, Деннис (24 января 2024 г.). «Эта знаменитая черная дыра получает второй взгляд — повторные исследования сверхмассивной черной дыры в галактике Мессье 87 подтверждают, что она продолжает действовать так, как предсказывала теория Эйнштейна». The New York Times . Архивировано из оригинала 24 января 2024 г. Получено 25 января 2024 г.
- ^ Overbye, Dennis (10 апреля 2019 г.). «Тьма наконец-то стала видна: астрономы сделали первое в истории изображение черной дыры». The New York Times . Архивировано из оригинала 21 мая 2019 г. Получено 11 апреля 2019 г.
- ^ AP (10 апреля 2019 г.). «Астрономы показали первую фотографию черной дыры». The New York Times (видео). Архивировано из оригинала 22 мая 2019 г. . Получено 11 апреля 2019 г. .
- ^ Doeleman, Shep (4 апреля 2016 г.). «Телескоп горизонта событий: визуализация и разрешение черной дыры во времени». Physics @ Berkeley . Событие происходит в 46:50. Архивировано из оригинала 1 декабря 2016 г. Получено 8 июля 2016 г.
- ^ Гроссман, Лиза; Коновер, Эмили (10 апреля 2019 г.). «Первая фотография черной дыры открывает новую эру астрофизики». Science News . Архивировано из оригинала 27 апреля 2019 г. . Получено 11 апреля 2019 г. .
- ^ В этой статье используется текст, доступный по лицензии CC BY 4.0. «Астрономы показали первое изображение черной дыры в сердце нашей галактики». eventhorizontelescope.org . 12 мая 2022 г. . Получено 22 июня 2022 г. .
- ^ C. Bower, Geoffrey (май 2022 г.). «В центре внимания первые результаты Sgr A* с помощью Event Horizon Telescope». The Astrophysical Journal Letters (2041–8205).
- ^ Сотрудничество Event Horizon Telescope (2021). "Результаты первых исследований M87 Event Horizon Telescope. VII. Поляризация кольца". The Astrophysical Journal . 910 (1): L12. arXiv : 2105.01169 . Bibcode : 2021ApJ...910L..12E. doi : 10.3847/2041-8213/abe71d . S2CID 233851995.
- ^ «Первое изображение черной дыры открывает новую эру астрофизики». Science News . 10 апреля 2019 г. Архивировано из оригинала 27 апреля 2019 г. Получено 30 сентября 2019 г.
- ^ Джонсон, MD; Фиш, VL; Доулман, SS; Марроне, DP; Пламбек, RL; Уордл, JFC; Акияма, K.; Асада, K.; Бодуан, C. (4 декабря 2015 г.). «Разрешенная структура магнитного поля и изменчивость вблизи горизонта событий Стрельца A*». Science . 350 (6265): 1242–1245. arXiv : 1512.01220 . Bibcode :2015Sci...350.1242J. doi :10.1126/science.aac7087. PMID 26785487. S2CID 21730194.
- ^ "Телескоп горизонта событий обнаружил магнитные поля в центральной черной дыре Млечного Пути". cfa.harvard.edu . 3 декабря 2015 г. Архивировано из оригинала 31 декабря 2015 г. Получено 12 января 2016 г.
- ^ Овербай, Деннис (26 апреля 2023 г.). «Свежий взгляд на все более знакомую черную дыру — радиоастрономы получили широкоугольное изображение одного из самых опасных мест в космосе». The New York Times . Архивировано из оригинала 26 апреля 2023 г. Получено 26 апреля 2023 г.
- ^ Лу, Ру-Сен и др. (26 апреля 2023 г.). «Кольцевидная структура аккреции в M87, соединяющая ее черную дыру и струю». Nature . 616 (7958): 686–690. arXiv : 2304.13252 . Bibcode :2023Natur.616..686L. doi :10.1038/s41586-023-05843-w. PMC 10132962 . PMID 37100940.
- ^ Overbye, Dennis (11 февраля 2016 г.). «Физики обнаруживают гравитационные волны, доказывая правоту Эйнштейна». The New York Times . Архивировано из оригинала 11 февраля 2016 г. Получено 11 февраля 2016 г.
- ^ Эбботт, Бенджамин П. и др. ( LIGO Scientific Collaboration & Virgo Collaboration ) (11 февраля 2016 г.). "Свойства слияния бинарных черных дыр GW150914". Physical Review Letters . 116 (24): 241102. arXiv : 1602.03840 . Bibcode : 2016PhRvL.116x1102A. doi : 10.1103/PhysRevLett.116.241102. PMID 27367378. S2CID 217406416.
- ^ ab Cardoso, V.; Franzin, E.; Pani, P. (2016). «Является ли гравитационно-волновое кольцо зондом горизонта событий?». Physical Review Letters . 116 (17): 171101. arXiv : 1602.07309 . Bibcode : 2016PhRvL.116q1101C. doi : 10.1103/PhysRevLett.116.171101. PMID 27176511. S2CID 206273829.
- ^ Abbott, Benjamin P.; et al. ( LIGO Scientific Collaboration & Virgo Collaboration ) (11 февраля 2016 г.). "Tests of general relativation with GW150914". Physical Review Letters . 116 (22): 221101. arXiv : 1602.03841 . Bibcode : 2016PhRvL.116v1101A. doi : 10.1103/PhysRevLett.116.221101. PMID 27314708. S2CID 217275338. Архивировано из оригинала 15 февраля 2016 г. Получено 12 февраля 2016 г.
- ^ ab Murk, Sebastian (2023). «Nomen non est omen: Почему слишком рано идентифицировать сверхкомпактные объекты как черные дыры». International Journal of Modern Physics D . 32 (14): 2342012–2342235. arXiv : 2210.03750 . Bibcode :2023IJMPD..3242012M. doi :10.1142/S0218271823420129. S2CID 252781040.
- ^ Эбботт, Б. П.; и др. ( LIGO Scientific Collaboration & Virgo Collaboration ) (2016). "Astrophysical Implications of the Binary Black Hole Merger GW150914". Astrophys. J. Lett . 818 (2): L22. arXiv : 1602.03846 . Bibcode : 2016ApJ...818L..22A. doi : 10.3847/2041-8205/818/2/L22 . hdl : 1826/11732. S2CID 209315965. Архивировано из оригинала 16 марта 2016 г.
- ^ "Обнаружение гравитационных волн". LIGO . Архивировано из оригинала 20 мая 2020 . Получено 9 апреля 2018 .
- ^ ab Gillessen, S.; Eisenhauer, F.; Trippe, S.; et al. (2009). «Мониторинг звездных орбит вокруг массивной черной дыры в центре Галактики». The Astrophysical Journal . 692 (2): 1075–1109. arXiv : 0810.4674 . Bibcode : 2009ApJ...692.1075G. doi : 10.1088/0004-637X/692/2/1075. S2CID 1431308.
- ^ ab Ghez, AM; Klein, BL; Morris, M.; et al. (1998). "Высокие собственные движущиеся звезды в окрестностях Стрельца A*: доказательства сверхмассивной черной дыры в центре нашей Галактики". The Astrophysical Journal . 509 (2): 678–686. arXiv : astro-ph/9807210 . Bibcode :1998ApJ...509..678G. doi :10.1086/306528. S2CID 18243528.
- ^ Бродерик, Эвери; Лёб, Абрахам; Нараян, Рамеш (август 2009 г.). «Горизонт событий Стрельца A*». The Astrophysical Journal . 701 (2): 1357–1366. arXiv : 0903.1105 . Bibcode : 2009ApJ...701.1357B. doi : 10.1088/0004-637X/701/2/1357. S2CID 12991878.
- ^ "NASA's NuSTAR видит редкое размытие света черной дыры". NASA . 12 августа 2014 г. Архивировано из оригинала 13 августа 2014 г. Получено 12 августа 2014 г.
- ^ "Исследователи проясняют динамику энергии вращения черной дыры". Архивировано из оригинала 17 сентября 2018 года . Получено 17 сентября 2018 года .
- ^ Marck, Jean-Alain (1 марта 1996 г.). "Сокращенный метод решения геодезических уравнений для черной дыры Шварцшильда". Classical and Quantum Gravity . 13 (3): 393–402. arXiv : gr-qc/9505010 . Bibcode : 1996CQGra..13..393M. doi : 10.1088/0264-9381/13/3/007. ISSN 0264-9381. S2CID 119508131.
- ^ ab McClintock, JE; Remillard, RA (2006). "Двойные черные дыры". В Lewin, W.; van der Klis, M. (ред.). Компактные звездные рентгеновские источники . стр. 157. arXiv : astro-ph/0306213 . Bibcode :2006csxs.book..157M. ISBN 978-0-521-82659-4.раздел 4.1.5.
- ^ «Что питает мощные струи черной дыры?». Наука | AAAS . 19 ноября 2014 г. Архивировано из оригинала 5 мая 2019 г. Получено 19 марта 2018 г.
- ^ abcdefghi Celotti, A.; Miller, JC; Sciama, DW (1999). "Astrophysical evidence for the exist of black holes" (PDF) . Classical and Quantum Gravity . 16 (12A): A3–A21. arXiv : astro-ph/9912186 . Bibcode :1999CQGra..16A...3C. doi :10.1088/0264-9381/16/12A/301. S2CID 17677758. Архивировано (PDF) из оригинала 27 июля 2018 г. . Получено 27 июля 2018 г. .
- ^ Winter, LM; Mushotzky, RF; Reynolds, CS (2006). "XMM-Newton Archival Study of the Ultralightous X-Ray Population in Nearby Galaxies". The Astrophysical Journal . 649 (2): 730–752. arXiv : astro-ph/0512480 . Bibcode : 2006ApJ...649..730W. doi : 10.1086/506579. S2CID 118445260.
- ^ information@eso.org. «Хаббл напрямую наблюдает диск вокруг черной дыры». www.spacetelescope.org . Архивировано из оригинала 8 марта 2016 года . Получено 7 марта 2016 года .
- ^ Муньос, Хосе А.; Медиавилла, Эвенсио; Кочанек, Кристофер С.; Фалько, Эмилио; Москера, Ана Мария (1 декабря 2011 г.). «Исследование цветности гравитационных линз с помощью космического телескопа Хаббл». Астрофизический журнал . 742 (2): 67. arXiv : 1107.5932 . Бибкод : 2011ApJ...742...67M. дои : 10.1088/0004-637X/742/2/67. S2CID 119119359.
- ^ Болтон, CT (1972). «Идентификация Cygnus X-1 с HDE 226868». Nature . 235 (5336): 271–273. Bibcode :1972Natur.235..271B. doi :10.1038/235271b0. S2CID 4222070.
- ^ Вебстер, Б. Л.; Мурдин, П. (1972). «Cygnus X-1 – спектрально-двойная звезда с тяжелым компаньоном?». Nature . 235 (5332): 37–38. Bibcode : 1972Natur.235...37W. doi : 10.1038/235037a0. S2CID 4195462.
- ^ Rolston, B. (10 ноября 1997 г.). "Первая черная дыра". Бюллетень . Университет Торонто. Архивировано из оригинала 2 мая 2008 г. Получено 11 марта 2008 г.
- ↑ Шипман, HL (1 января 1975 г.). «Неправдоподобная история моделей тройных звезд для Лебедя X-1. Доказательства существования черной дыры». Astrophysical Letters . 16 (1): 9–12. Bibcode : 1975ApL....16....9S.
- ^ "Ученые НАСА определили наименьшую известную черную дыру" (пресс-релиз). Goddard Space Flight Center . 1 апреля 2008 г. Архивировано из оригинала 27 декабря 2008 г. Получено 14 марта 2009 г.
- ^ Chou, Felicia; Anderson, Janet; Watzke, Megan (5 января 2015 г.). "RELEASE 15-001 – NASA's Chandra обнаруживает рекордный выброс из черной дыры Млечного Пути". NASA . Архивировано из оригинала 6 января 2015 г. . Получено 6 января 2015 г. .
- ^ Кролик, Дж. Х. (1999). Активные ядра галактик. Princeton University Press. Гл. 1.2. ISBN 978-0-691-01151-6. Архивировано из оригинала 14 августа 2021 г. . Получено 16 октября 2020 г. .
- ^ Sparke, LS ; Gallagher, JS (2000). Галактики во Вселенной: Введение. Cambridge University Press. Гл. 9.1. ISBN 978-0-521-59740-1. Архивировано из оригинала 22 марта 2022 . Получено 16 октября 2020 .
- ^ Kormendy, J.; Richstone, D. (1995). «Inward Bound – The Search For Supermassive Black Holes In Galactic Nuclei». Annual Review of Astronomy and Astrophysics . 33 (1): 581–624. Bibcode : 1995ARA&A..33..581K. doi : 10.1146/annurev.aa.33.090195.003053.
- ^ Кинг, А. (2003). «Черные дыры, образование галактик и соотношение MBH-σ». The Astrophysical Journal Letters . 596 (1): 27–29. arXiv : astro-ph/0308342 . Bibcode : 2003ApJ...596L..27K. doi : 10.1086/379143. S2CID 9507887.
- ^ Феррарезе, Л.; Мерритт, Д. (2000). «Фундаментальная связь между сверхмассивными черными дырами и их родительскими галактиками». The Astrophysical Journal Letters . 539 (1): 9–12. arXiv : astro-ph/0006053 . Bibcode : 2000ApJ...539L...9F. doi : 10.1086/312838. S2CID 6508110.
- ^ Bennett, DP; Becker, AC; Quinn, JL; Tomaney, AB; Alcock, C.; Allsman, RA; Alves, DR; Axelrod, TS; Calitz, JJ; Cook, KH; Drake, AJ; Fragile, PC; Freeman, KC; Geha, M.; Griest, K. (1 ноября 2002 г.). «События гравитационного микролинзирования, вызванные черными дырами звездной массы». The Astrophysical Journal . 579 (2): 639–659. arXiv : astro-ph/0109467 . Bibcode :2002ApJ...579..639B. doi :10.1086/342225. ISSN 0004-637X.
- ^ Mao, Shude; Smith, Martin C.; Woźniak, P.; Udalski, A.; Szymański, M.; Kubiak, M.; Pietrzyński, G.; Soszyński, I.; Żebruń, K. (1 января 2002 г.). "Optical Gravitational Lensing Experiment OGLE-1999-BUL-32: the longest ever microlensing event - evidence for a stellar mass black hole?". Monthly Notices of the Royal Astronomical Society . 329 (2): 349–354. arXiv : astro-ph/0108312 . Bibcode : 2002MNRAS.329..349M. doi : 10.1046/j.1365-8711.2002.04986.x . ISSN 0035-8711.
- ^ Sahu, KC (2022). «Изолированная черная дыра звездной массы, обнаруженная с помощью астрометрического микролинзирования». Astrophysical Journal . 933 (1): 83. arXiv : 2201.13296 . Bibcode : 2022ApJ...933...83S. doi : 10.3847/1538-4357/ac739e . S2CID 246430448.
- ^ Bozza, V. (2010). «Гравитационное линзирование черными дырами». Общая теория относительности и гравитация . 42 (9): 2269–2300. arXiv : 0911.2187 . Bibcode :2010GReGr..42.2269B. doi :10.1007/s10714-010-0988-2. S2CID 118635353.
- ^ Kovacs, Z.; Cheng, KS; Harko, T. (2009). «Могут ли черные дыры звездной массы быть кварковыми звездами?». Monthly Notices of the Royal Astronomical Society . 400 (3): 1632–1642. arXiv : 0908.2672 . Bibcode : 2009MNRAS.400.1632K. doi : 10.1111/j.1365-2966.2009.15571.x . S2CID 18263809.
- ^ Кусенко, А. (2006). "Свойства и сигнатуры суперсимметричных Q-шаров". arXiv : hep-ph/0612159 .
- ^ Ханссон, Дж.; Сэндин, Ф. (2005). «Преонные звезды: новый класс космических компактных объектов». Physics Letters B. 616 ( 1–2): 1–7. arXiv : astro-ph/0410417 . Bibcode : 2005PhLB..616....1H. doi : 10.1016/j.physletb.2005.04.034. S2CID 119063004.
- ^ Кифер, К. (2006). «Квантовая гравитация: общее введение и последние разработки». Annalen der Physik . 15 (1–2): 129–148. arXiv : gr-qc/0508120 . Bibcode : 2006AnP...518..129K. doi : 10.1002/andp.200510175. S2CID 12984346.
- ^ Матур, Самир Д. (2005). «Предложение о черных дырах: элементарный обзор». Fortschritte der Physik . 53 (7–8): 793. arXiv : hep-th/0502050 . Бибкод : 2005ДляФ..53..793М. дои : 10.1002/prop.200410203. S2CID 15083147.
- ^ Скендерис, К.; Тейлор, М. (2008). «Предложение о пушистом шаре для черных дыр». Physics Reports . 467 (4–5): 117. arXiv : 0804.0552 . Bibcode : 2008PhR...467..117S. doi : 10.1016/j.physrep.2008.08.001. S2CID 118403957.
- ^ Мазур, Павел О.; Моттола, Эмиль (2004). «Гравитационные вакуумные конденсатные звезды». Труды Национальной академии наук Соединенных Штатов Америки . 101 (26): 9545–9550. arXiv : gr-qc/0407075 . Bibcode : 2004PNAS..101.9545M . doi : 10.1073/pnas.0402717101 . PMC 470711. PMID 15210982. S2CID 2607263.
- ^ Чой, Чарльз К. (2018). «Черные дыры-претенденты могли бы действительно быть странными квантовыми звездами». Scientific American . Архивировано из оригинала 17 июня 2019 года . Получено 17 марта 2018 года .
- ^ Макрей, Майк (20 февраля 2024 г.). «Пузыристые «звезды внутри звезд» могли бы объяснить странности черных дыр». ScienceAlert . Архивировано из оригинала 20 февраля 2024 г. . Получено 20 февраля 2024 г. .
- ↑ Болл, Филипп (31 марта 2005 г.). «Черные дыры «не существуют»". Природа . doi :10.1038/news050328-8.
- ^ Хокинг, SW (1971). «Гравитационное излучение от сталкивающихся черных дыр». Physical Review Letters . 26 (21): 1344–1346. Bibcode : 1971PhRvL..26.1344H. doi : 10.1103/PhysRevLett.26.1344.
- ^ ab Wald, RM (2001). "Термодинамика черных дыр". Living Reviews in Relativity . 4 (1): 6. arXiv : gr-qc/9912119 . Bibcode : 2001LRR.....4....6W. doi : 10.12942/lrr-2001-6 . PMC 5253844. PMID 28163633 .
- ^ 't Hooft, G. (2001). "Голографический принцип". В Zichichi, A. (ред.). Основы и основные моменты фундаментальной физики . Субъядерная серия. Том 37. World Scientific Publishing . стр. 72–100. arXiv : hep-th/0003004 . Bibcode : 2001bhfp.conf...72T. doi : 10.1142/9789812811585_0005. ISBN 978-981-02-4536-8. S2CID 119383028.
- ^ Стромингер, А.; Вафа, К. (1996). «Микроскопическое происхождение энтропии Бекенштейна-Хокинга». Physics Letters B. 379 ( 1–4): 99–104. arXiv : hep-th/9601029 . Bibcode : 1996PhLB..379...99S. doi : 10.1016/0370-2693(96)00345-0. S2CID 1041890.
- ^ Карлип, С. (2009). "Термодинамика и статистическая механика черных дыр". Физика черных дыр . Конспект лекций по физике. Том 769. Берлин, Гейдельберг. С. 89–123. arXiv : 0807.4520 . Bibcode :2009LNP...769...89C. doi :10.1007/978-3-540-88460-6_3. ISBN 978-3-540-88459-0. S2CID 15877702.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Хокинг, SW "Играет ли Бог в кости?". www.hawking.org.uk . Архивировано из оригинала 11 января 2012 года . Получено 14 марта 2009 года .
- ^ Гиддингс, СБ (1995). "Информационный парадокс черной дыры". Частицы, струны и космология . Семинар Джонса Хопкинса по текущим проблемам теории частиц 19 и междисциплинарный симпозиум PASCOS 5. arXiv : hep-th/9508151 . Bibcode : 1995hep.th....8151G.
- ^ ab Unruh, William G. ; Wald, Robert M. (2017). «Потеря информации». Reports on Progress in Physics . 80 (9): 092002. arXiv : 1703.02140 . Bibcode :2017RPPh...80i2002U. doi :10.1088/1361-6633/aa778e. PMID 28585922. S2CID 39957660.
- ^ Матур, SD (2011). Информационный парадокс: конфликты и разрешения . XXV Международный симпозиум по взаимодействиям лептон-фотонов при высоких энергиях. Pramana . Т. 79, № 5. С. 1059–1073. arXiv : 1201.2079 . Bibcode : 2012Prama..79.1059M. doi : 10.1007/s12043-012-0417-z.
- ^ Page, Don N. (1993). «Информация в излучении черной дыры». Phys. Rev. Lett. 71 (23): 3743–3746. arXiv : hep-th/9306083 . Bibcode :1993PhRvL..71.3743P. CiteSeerX 10.1.1.267.174 . doi :10.1103/PhysRevLett.71.3743. PMID 10055062. S2CID 9363821.
- ^ Page, Don N. (1993). "Средняя энтропия подсистемы". Phys. Rev. Lett. 71 (9): 1291–1294. arXiv : gr-qc/9305007 . Bibcode :1993PhRvL..71.1291P. CiteSeerX 10.1.1.339.7694 . doi :10.1103/PhysRevLett.71.1291. PMID 10055503. S2CID 17058654.
- ↑ Merali, Zeeya (3 апреля 2013 г.). «Астрофизика: Огонь в дыре!». Nature . 496 (7443): 20–23. Bibcode : 2013Natur.496...20M. doi : 10.1038/496020a . PMID 23552926.
- ^ Амхейри, Ахмед; Марольф, Дональд; Полчински, Джозеф; Салли, Джеймс (2013). «Черные дыры: дополнительность или брандмауэры?». Журнал физики высоких энергий . 2013 (2): 62. arXiv : 1207.3123 . Bibcode : 2013JHEP...02..062A. doi : 10.1007/JHEP02(2013)062. S2CID 55581818.
Источники
- Кэрролл, Шон М. (2004). Пространство-время и геометрия . Эддисон Уэсли. ISBN 978-0-8053-8732-2., конспекты лекций, на которых основана книга, доступны бесплатно на сайте Шона Кэрролла Архивировано 23 марта 2017 г. на Wayback Machine
- Хокинг, SW ; Эллис, GFR (1973). Крупномасштабная структура пространства-времени. Cambridge University Press. ISBN 978-0-521-09906-6. Архивировано из оригинала 21 июля 2020 . Получено 16 мая 2020 .
- Мизнер, Чарльз ; Торн, Кип С.; Уиллер , Джон (1973). Гравитация . WH Freeman and Company. ISBN 978-0-7167-0344-0.
- Торн, Кип С. (1994). Черные дыры и искривления времени . Norton, WW & Company, Inc. ISBN 978-0-393-31276-8.
- Уолд, Роберт М. (1984). Общая теория относительности. Издательство Чикагского университета. ISBN 978-0-226-87033-5. Архивировано из оригинала 11 августа 2016 . Получено 23 февраля 2016 .
- Уилер, Дж. Крейг (2007). Космические катастрофы (2-е изд.). Cambridge University Press. ISBN 978-0-521-85714-7.
Дальнейшее чтение
Популярное чтение
- Бегельман, Митчелл К.; Риз, Мартин Дж. (2021). Фатальное притяжение гравитации: черные дыры во вселенной (3-е изд.). Кембридж, Великобритания; Нью-Йорк, Нью-Йорк: Cambridge University Press. ISBN 978-1-108-87112-9.
- Фергюсон, Китти (1991). Черные дыры в пространстве-времени . Уоттс Франклин. ISBN 978-0-531-12524-3.
- Хокинг, Стивен (1988). Краткая история времени . Bantam Books, Inc. ISBN 978-0-553-38016-3.
- Хокинг, Стивен ; Пенроуз, Роджер (1996). Природа пространства и времени. Princeton University Press. ISBN 978-0-691-03791-2. Архивировано из оригинала 18 октября 2021 г. . Получено 16 мая 2020 г. .
- Левин, Джанна (2020). Руководство по выживанию в черной дыре. Нью-Йорк: Альфред А. Кнопф. ISBN 9780525658221. Архивировано из оригинала 22 марта 2022 г. . Получено 6 ноября 2021 г. .
- Мелиа, Фульвио (2003). Черная дыра в центре нашей Галактики . Princeton U Press. ISBN 978-0-691-09505-9.
- Мелиа, Фульвио (2003). Грань бесконечности. Сверхмассивные черные дыры во Вселенной . Cambridge U Press. ISBN 978-0-521-81405-8.
- Pickover, Clifford (1998). Черные дыры: Путеводитель . Wiley, John & Sons, Inc. ISBN 978-0-471-19704-1.
- Сасскинд, Леонард (2008). Война черных дыр: моя битва со Стивеном Хокингом за то, чтобы сделать мир безопасным для квантовой механики (1-е изд.). Нью-Йорк: Little, Brown. ISBN 978-0-316-01640-7. OCLC 181603165.
Университетские учебники и монографии
- Картер, Б. (1973). "Состояния равновесия черной дыры". В DeWitt-Morette, Cécile; DeWitt, Bryce S. (ред.). Черные дыры . Нью-Йорк: Gordon and Breach. ISBN 978-0-677-15610-1.
- Чандрасекар, Субраманьян (1999). Математическая теория черных дыр . Oxford University Press. ISBN 978-0-19-850370-5.
- Фролов, Валерий П.; Новиков, Игорь Д. (1998). Физика черных дыр . Фундаментальные теории физики. Т. 96. doi :10.1007/978-94-011-5139-9. ISBN 978-0-7923-5146-7.
- Фролов, Валерий П.; Зельников, Андрей (2011). Введение в физику черных дыр. Оксфорд: Oxford University Press. ISBN 978-0-19-969229-3. Zbl 1234.83001. Архивировано из оригинала 22 марта 2022 г. . Получено 2 января 2022 г. .
- Мелиа, Фульвио (2007). Галактическая сверхмассивная черная дыра . Princeton U Press. ISBN 978-0-691-13129-0.
- Тейлор, Эдвин Ф.; Уилер, Джон Арчибальд (2000). Исследование черных дыр . Эддисон Уэсли Лонгман. ISBN 978-0-201-38423-9.
- Уолд, Роберт М. (1992). Пространство, время и гравитация: теория Большого взрыва и черных дыр . Издательство Чикагского университета. ISBN 978-0-226-87029-8.
- Прайс, Ричард; Крейтон, Тевиет (2008). «Черные дыры». Scholarpedia . 3 (1): 4277. Bibcode :2008SchpJ...3.4277C. doi : 10.4249/scholarpedia.4277 .
Обзорные статьи
- Хьюз, Скотт А. (2005). «Доверяй, но проверяй: аргументы в пользу астрофизических черных дыр». arXiv : hep-ph/0511217 .Конспект лекций Летнего института SLAC 2005 года .
- Галло, Елена; Марольф, Дональд (2009). «Ресурсное письмо BH-2: Черные дыры». American Journal of Physics . 77 (4): 294–307. arXiv : 0806.2316 . Bibcode : 2009AmJPh..77..294G. doi : 10.1119/1.3056569. S2CID 118494056.
- Кардосо, Витор; Пани, Паоло (2019). «Проверка природы темных компактных объектов: отчет о состоянии». Living Reviews in Relativity . 22 (1): 4. arXiv : 1904.05363 . Bibcode : 2019LRR....22....4C. doi : 10.1007/s41114-019-0020-4. S2CID 256465740.
- Манн, Роберт Б.; Мурк, Себастьян; Терно, Дэниел Р. (2022). «Черные дыры и их горизонты в полуклассических и модифицированных теориях гравитации». International Journal of Modern Physics D . 31 (9): 2230015–2230276. arXiv : 2112.06515 . Bibcode :2022IJMPD..3130015M. doi :10.1142/S0218271822300154. S2CID 245123647.
Внешние ссылки
- Черные дыры в программе In Our Time на BBC
- Стэнфордская энциклопедия философии : «Сингулярности и черные дыры» Эрика Куриела и Питера Бокулича.
- Черные дыры: неумолимое притяжение гравитации – Интерактивный мультимедийный веб-сайт о физике и астрономии черных дыр от Научного института космического телескопа (HubbleSite)
- Визуализация черной дыры ЕКА, архивированная 3 мая 2019 г. на Wayback Machine
- Часто задаваемые вопросы (FAQ) о черных дырах
- Геометрия Шварцшильда
- Черные дыры - основы (NYT; апрель 2021 г.)
Видео
- 16-летнее исследование отслеживает звезды, вращающиеся вокруг Стрельца А*
- Фильм кандидата в черные дыры от Института Макса Планка
- Коуэн, Рон (20 апреля 2015 г.). «Трехмерное моделирование сталкивающихся черных дыр признано самым реалистичным». Nature . doi : 10.1038/nature.2015.17360 .
- Компьютерная визуализация сигнала, обнаруженного LIGO
- Две черные дыры сливаются в одну (на основе сигнала GW150914)

























