Введение в общую теорию относительности

Общая теория относительности
${\displaystyle G_{\mu \nu }+\Lambda g_ {\mu \nu } = {\kappa }T_ {\mu \nu }}$
Введение История Хронология Тесты Математическая формулировка
Фундаментальные концепции Принцип эквивалентности Специальная теория относительности Мировая линия Псевдориманово многообразие
Феномены проблема Кеплера Гравитационное линзирование Гравитационное красное смещение Гравитационное замедление времени Гравитационные волны Перетаскивание кадров Геодезический эффект Горизонт событий Сингулярность Черная дыра Пространство-время Диаграммы пространства-времени пространство-время Минковского Мост Эйнштейна-Розена
Уравнения Формализмы Уравнения Линеаризованная гравитация Уравнения поля Эйнштейна Фридман Геодезические Mathisson–Papapetrou–Dixon Hamilton–Jacobi–Einstein Formalisms ADM BSSN Post-Newtonian Advanced theory Kaluza–Klein theory Quantum gravity
Solutions Schwarzschild (interior) Reissner–Nordström Einstein–Rosen waves Wormhole Gödel Kerr Kerr–Newman Kerr–Newman–de Sitter Kasner Lemaître–Tolman Taub–NUT Milne Robertson–Walker Oppenheimer–Snyder pp-wave van Stockum dust Weyl−Lewis−Papapetrou Hartle–Thorne
Scientists Einstein Lorentz Hilbert Poincaré Schwarzschild de Sitter Reissner Nordström Weyl Eddington Friedmann Milne Zwicky Lemaître Oppenheimer Gödel Wheeler Robertson Bardeen Walker Kerr Chandrasekhar Ehlers Penrose Hawking Raychaudhuri Taylor Hulse van Stockum Taub Newman Yau Thorne others
Physics portal  Category
v t e

Общая теория относительности — теория гравитации , разработанная Альбертом Эйнштейном в период с 1907 по 1915 год. Общая теория относительности утверждает, что наблюдаемый гравитационный эффект между массами является результатом искривления ими пространства-времени .

К началу 20-го века закон всемирного тяготения Ньютона был принят более двухсот лет назад как допустимое описание силы тяготения между массами. В модели Ньютона гравитация является результатом силы притяжения между массивными объектами. Хотя даже Ньютон был обеспокоен неизвестной природой этой силы, базовая структура была чрезвычайно успешной в описании движения.

Эксперименты и наблюдения показывают, что описание гравитации Эйнштейном учитывает несколько эффектов , которые не объясняются законом Ньютона, например, мельчайшие аномалии в орбитах Меркурия и других планет . Общая теория относительности также предсказывает новые эффекты гравитации, такие как гравитационные волны , гравитационное линзирование и влияние гравитации на время, известное как гравитационное замедление времени . Многие из этих предсказаний были подтверждены экспериментом или наблюдением, в последнее время гравитационные волны .

Общая теория относительности превратилась в важный инструмент современной астрофизики . Она обеспечивает основу для современного понимания черных дыр , областей пространства, где гравитационное воздействие настолько сильно, что даже свет не может вырваться. Считается, что их сильная гравитация ответственна за интенсивное излучение, испускаемое некоторыми типами астрономических объектов (такими как активные ядра галактик или микроквазары ). Общая теория относительности также является частью структуры стандартной модели Большого взрыва в космологии .

Хотя общая теория относительности не является единственной релятивистской теорией гравитации, она является самой простой, которая согласуется с экспериментальными данными. Тем не менее, остается ряд открытых вопросов, наиболее фундаментальным из которых является то, как общая теория относительности может быть согласована с законами квантовой физики, чтобы создать полную и самосогласованную теорию квантовой гравитации .

В сентябре 1905 года Альберт Эйнштейн опубликовал свою теорию специальной теории относительности , которая примиряет законы движения Ньютона с электродинамикой (взаимодействием между объектами с электрическим зарядом ). Специальная теория относительности ввела новую структуру для всей физики, предложив новые концепции пространства и времени. Некоторые принятые в то время физические теории не соответствовали этой структуре; ключевым примером была теория гравитации Ньютона , которая описывает взаимное притяжение, испытываемое телами из-за их массы.

Несколько физиков, включая Эйнштейна, искали теорию, которая бы примирила закон тяготения Ньютона и специальную теорию относительности. Только теория Эйнштейна оказалась согласующейся с экспериментами и наблюдениями. Чтобы понять основные идеи теории, полезно проследить ход мыслей Эйнштейна между 1907 и 1915 годами, от его простого мысленного эксперимента с участием наблюдателя в свободном падении до его полностью геометрической теории гравитации. ^[1]

Человек в свободно падающем лифте испытывает невесомость ; объекты либо парят неподвижно, либо дрейфуют с постоянной скоростью. Поскольку все в лифте падает вместе, никакого гравитационного эффекта не наблюдается. Таким образом, опыт наблюдателя в свободном падении неотличим от опыта наблюдателя в глубоком космосе, вдали от любого значительного источника гравитации. Такие наблюдатели являются привилегированными («инерционными») наблюдателями, описанными Эйнштейном в его специальной теории относительности : наблюдатели, для которых свет движется по прямым линиям с постоянной скоростью. ^[2]

Эйнштейн выдвинул гипотезу, что схожие ощущения невесомых наблюдателей и инерциальных наблюдателей в специальной теории относительности представляют собой фундаментальное свойство гравитации, и он сделал это краеугольным камнем своей общей теории относительности, формализованной в его принципе эквивалентности . Грубо говоря, принцип гласит, что человек в свободно падающем лифте не может сказать, что он находится в свободном падении. Каждый эксперимент в такой среде свободного падения имеет те же результаты, что и для наблюдателя, находящегося в покое или равномерно движущегося в глубоком космосе, вдали от всех источников гравитации. ^[3]

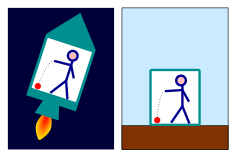
Большинство эффектов гравитации исчезают при свободном падении , но эффекты, которые кажутся такими же, как эффекты гравитации, могут быть получены ускоренной системой отсчета . Наблюдатель в закрытой комнате не может сказать, какой из следующих двух сценариев является верным:

• Предметы падают на пол, потому что комната покоится на поверхности Земли, и предметы тянутся вниз под действием силы тяжести.
• Предметы падают на пол, потому что комната находится на борту ракеты в космосе, которая ускоряется со скоростью 9,81 м/с ² , стандартной гравитацией на Земле, и находится далеко от любого источника гравитации. Предметы тянутся к полу той же «силой инерции», которая вдавливает водителя ускоряющегося автомобиля в спинку сиденья.

Наоборот, любой эффект, наблюдаемый в ускоренной системе отсчета, должен наблюдаться и в гравитационном поле соответствующей силы. Этот принцип позволил Эйнштейну предсказать несколько новых эффектов гравитации в 1907 году ( см. § Физические последствия, ниже ).

Наблюдатель в ускоренной системе отсчета должен ввести то, что физики называют фиктивными силами , чтобы учесть ускорение, испытываемое наблюдателем и объектами вокруг него. В примере с водителем, вдавливаемым в сиденье, сила, ощущаемая водителем, является одним примером; другим примером является сила, которую можно почувствовать, потянув руки вверх и наружу, если попытаться вращаться как волчок. Главное понимание Эйнштейна состояло в том, что постоянное, знакомое притяжение гравитационного поля Земли в основе своей такое же, как эти фиктивные силы . ^[4] Кажущаяся величина фиктивных сил всегда кажется пропорциональной массе любого объекта, на который они действуют — например, сиденье водителя оказывает ровно столько силы, чтобы ускорить водителя с той же скоростью, что и автомобиль. По аналогии Эйнштейн предположил, что объект в гравитационном поле должен чувствовать гравитационную силу, пропорциональную его массе, как это воплощено в законе тяготения Ньютона . ^[5]

В 1907 году Эйнштейну оставалось еще восемь лет до завершения общей теории относительности. Тем не менее, он смог сделать ряд новых, проверяемых предсказаний, которые основывались на его отправной точке для разработки новой теории: принципе эквивалентности. ^[6]

Первый новый эффект — это гравитационный сдвиг частоты света. Рассмотрим двух наблюдателей на борту ускоряющегося ракетного корабля. На борту такого корабля существует естественное понятие «вверх» и «вниз»: направление, в котором ускоряется корабль, — «вверх», а свободно плавающие объекты ускоряются в противоположном направлении, падая «вниз». Предположим, что один из наблюдателей находится «выше» другого. Когда нижний наблюдатель посылает световой сигнал верхнему наблюдателю, ускорение корабля приводит к тому, что свет смещается в красную область спектра , что можно рассчитать с помощью специальной теории относительности ; второй наблюдатель измерит более низкую частоту света, чем первый отправленный. И наоборот, свет, отправленный от верхнего наблюдателя к нижнему , смещается в синюю область спектра , то есть смещается в сторону более высоких частот. ^[7] Эйнштейн утверждал, что такие сдвиги частоты также должны наблюдаться в гравитационном поле. Это показано на рисунке слева, где показана световая волна, которая постепенно смещается в красную сторону по мере продвижения вверх против гравитационного ускорения. Этот эффект был подтвержден экспериментально, как описано ниже.

Этот гравитационный сдвиг частоты соответствует гравитационному замедлению времени : поскольку «более высокий» наблюдатель измеряет ту же световую волну, чтобы получить более низкую частоту, чем «более низкий» наблюдатель, время должно идти быстрее для более высокого наблюдателя. Таким образом, время идет тем медленнее для наблюдателей, чем ниже они находятся в гравитационном поле.

Важно подчеркнуть, что для каждого наблюдателя нет наблюдаемых изменений течения времени для событий или процессов, которые находятся в состоянии покоя в его или ее системе отсчета. Пятиминутные яйца, отсчитываемые часами каждого наблюдателя, имеют одинаковую последовательность; по прошествии одного года на каждых часах каждый наблюдатель стареет на эту величину; короче говоря, каждые часы находятся в идеальном согласии со всеми процессами, происходящими в их непосредственной близости. Только когда часы сравниваются между отдельными наблюдателями, можно заметить, что время идет медленнее для нижнего наблюдателя, чем для верхнего. ^[8] Этот эффект незначительный, но он также был подтвержден экспериментально в нескольких экспериментах, как описано ниже.

Аналогичным образом Эйнштейн предсказал гравитационное отклонение света : в гравитационном поле свет отклоняется вниз, к центру гравитационного поля. Количественно его результаты были ошибочны в два раза; правильный вывод требует более полной формулировки общей теории относительности, а не только принципа эквивалентности. ^[9]

Эквивалентность гравитационных и инерционных эффектов не составляет полной теории гравитации. Когда дело доходит до объяснения гравитации вблизи нашего собственного местоположения на поверхности Земли, замечание о том, что наша система отсчета не находится в свободном падении, так что следует ожидать фиктивных сил , дает подходящее объяснение. Но свободно падающая система отсчета на одной стороне Земли не может объяснить, почему люди на противоположной стороне Земли испытывают гравитационное притяжение в противоположном направлении.

Более простое проявление того же эффекта включает два тела, которые падают бок о бок к Земле с одинаковым положением и скоростью. В системе отсчета, которая находится в свободном падении рядом с этими телами, они кажутся парящими в невесомости — но не совсем так. Эти тела падают не в точно одном и том же направлении, а к одной точке в пространстве: а именно, к центру тяжести Земли . Следовательно, есть компонент движения каждого тела по направлению к другому (см. рисунок). В небольшой среде, такой как свободно падающий лифт, это относительное ускорение ничтожно, в то время как для парашютистов на противоположных сторонах Земли эффект велик. Такие различия в силе также ответственны за приливы в океанах Земли, поэтому для этого явления используется термин « приливной эффект ».

Эквивалентность между инерцией и гравитацией не может объяснить приливные эффекты – она не может объяснить изменения в гравитационном поле. ^[10] Для этого необходима теория, описывающая способ, которым материя (например, большая масса Земли) влияет на инерционную среду вокруг нее.

Пока Эйнштейн исследовал эквивалентность гравитации и ускорения, а также роль приливных сил, он обнаружил несколько аналогий с геометрией поверхностей . Примером может служить переход от инерциальной системы отсчета (в которой свободные частицы движутся по прямым траекториям с постоянной скоростью) к вращающейся системе отсчета (в которой для объяснения движения частиц необходимо вводить фиктивные силы ): это аналогично переходу от декартовой системы координат ( в которой координатные линии являются прямыми) к искривленной системе координат (где координатные линии не обязательно должны быть прямыми).

Более глубокая аналогия связывает приливные силы со свойством поверхностей, называемым кривизной . Для гравитационных полей отсутствие или наличие приливных сил определяет, можно ли устранить влияние гравитации, выбрав свободно падающую систему отсчета. Аналогично, отсутствие или наличие кривизны определяет, эквивалентна ли поверхность плоскости . Летом 1912 года, вдохновленный этими аналогиями, Эйнштейн искал геометрическую формулировку гравитации. ^[11]

Элементарные объекты геометрии  – точки , линии , треугольники  – традиционно определяются в трехмерном пространстве или на двумерных поверхностях . В 1907 году Герман Минковский , бывший профессор математики Эйнштейна в Швейцарском федеральном политехническом институте, представил пространство Минковского , геометрическую формулировку специальной теории относительности Эйнштейна , где геометрия включала не только пространство , но и время. Основной сущностью этой новой геометрии является четырехмерное пространство -время . Орбиты движущихся тел являются кривыми в пространстве-времени ; орбиты тел, движущихся с постоянной скоростью без изменения направления, соответствуют прямым линиям. ^[12]

Геометрия общих кривых поверхностей была разработана в начале 19 века Карлом Фридрихом Гауссом . Эта геометрия в свою очередь была обобщена на пространства более высоких измерений в римановой геометрии, введенной Бернхардом Риманом в 1850-х годах. С помощью римановой геометрии Эйнштейн сформулировал геометрическое описание гравитации, в котором пространство-время Минковского заменено искаженным, искривленным пространством-временем, так же как искривленные поверхности являются обобщением обычных плоских поверхностей. Диаграммы вложений используются для иллюстрации искривленного пространства-времени в образовательных контекстах. ^{[13] [14]}

После того, как он осознал справедливость этой геометрической аналогии, Эйнштейну потребовалось еще три года, чтобы найти недостающий краеугольный камень своей теории: уравнения, описывающие, как материя влияет на кривизну пространства-времени. Сформулировав то, что сейчас известно как уравнения Эйнштейна (или, точнее, его уравнения поля гравитации), он представил свою новую теорию гравитации на нескольких сессиях Прусской академии наук в конце 1915 года, достигнув кульминации в своем последнем докладе 25 ноября 1915 года. ^[15]

Перефразируя Джона Уиллера , геометрическую теорию гравитации Эйнштейна можно обобщить следующим образом: пространство-время говорит материи, как двигаться; материя говорит пространству-времени, как искривляться . ^[16] Что это значит, рассматривается в следующих трех разделах, в которых исследуется движение так называемых пробных частиц , исследуются свойства материи, служащие источником гравитации, и, наконец, вводятся уравнения Эйнштейна, которые связывают эти свойства материи с кривизной пространства-времени.

Чтобы отобразить гравитационное влияние тела, полезно подумать о том, что физики называют пробными или тестовыми частицами : частицами, на которые влияет гравитация, но которые настолько малы и легки, что мы можем пренебречь их собственным гравитационным эффектом. В отсутствие гравитации и других внешних сил тестовая частица движется по прямой линии с постоянной скоростью. На языке пространства-времени это эквивалентно утверждению, что такие тестовые частицы движутся по прямым мировым линиям в пространстве-времени. При наличии гравитации пространство-время является неевклидовым или искривленным , и в искривленном пространстве-времени прямые мировые линии могут не существовать. Вместо этого тестовые частицы движутся по линиям, называемым геодезическими , которые являются «настолько прямыми, насколько это возможно», то есть они следуют по кратчайшему пути между начальной и конечной точками, принимая во внимание кривизну.

Простая аналогия такова: в геодезии , науке об измерении размеров и формы Земли, геодезическая линия — это кратчайший путь между двумя точками на поверхности Земли. Приблизительно, такой путь — это сегмент большого круга , например, линия долготы или экватор . Эти пути, конечно, не прямые, просто потому, что они должны следовать кривизне поверхности Земли. Но они настолько прямые, насколько это возможно при соблюдении этого ограничения.

Свойства геодезических линий отличаются от свойств прямых линий. Например, на плоскости параллельные линии никогда не пересекаются, но это не так для геодезических линий на поверхности Земли: например, линии долготы параллельны на экваторе, но пересекаются на полюсах. Аналогично, мировые линии пробных частиц в свободном падении являются геодезическими пространства-времени , самыми прямыми из возможных линий в пространстве-времени. Но все же есть существенные различия между ними и действительно прямыми линиями, которые можно проследить в пространстве-времени без гравитации специальной теории относительности. В специальной теории относительности параллельные геодезические остаются параллельными. В гравитационном поле с приливными эффектами это, в общем случае, не будет иметь места. Если, например, два тела изначально находятся в состоянии покоя относительно друг друга, но затем падают в гравитационное поле Земли, они будут двигаться навстречу друг другу, падая к центру Земли. ^[17]

По сравнению с планетами и другими астрономическими телами, объекты повседневной жизни (люди, машины, дома, даже горы) имеют небольшую массу. Когда речь идет о таких объектах, законы, управляющие поведением пробных частиц, достаточны для описания того, что происходит. В частности, чтобы отклонить пробную частицу от ее геодезической траектории, должна быть применена внешняя сила. Стул, на котором кто-то сидит, прикладывает внешнюю направленную вверх силу, не позволяя человеку свободно падать к центру Земли и, таким образом, следовать геодезической, что он в противном случае делал бы без стула или любого другого вещества между ним и центральной точкой Земли. Таким образом, общая теория относительности объясняет ежедневное ощущение гравитации на поверхности Земли не как тягу вниз гравитационной силы, а как толчок вверх внешних сил. Эти силы отклоняют все тела, покоящиеся на поверхности Земли, от геодезических, которым они в противном случае следовали бы. ^[18] Для объектов, достаточно массивных, чтобы их собственным гравитационным влиянием нельзя было пренебречь, законы движения несколько сложнее, чем для тестовых частиц, хотя остается верным, что пространство-время говорит материи, как ей двигаться. ^[19]

В описании гравитации Ньютоном гравитационная сила вызвана материей. Точнее, она вызвана определенным свойством материальных объектов: их массой . В теории Эйнштейна и связанных с ней теориях гравитации кривизна в каждой точке пространства-времени также вызвана любой присутствующей материей. Здесь также масса является ключевым свойством в определении гравитационного влияния материи. Но в релятивистской теории гравитации масса не может быть единственным источником гравитации. Относительность связывает массу с энергией, а энергию с импульсом.

Эквивалентность между массой и энергией , выраженная формулой E  =  mc2 , является самым известным следствием специальной теории относительности. В теории относительности масса и энергия являются двумя различными способами описания одной физической величины. Если физическая система имеет энергию, она также имеет соответствующую массу, и наоборот. В частности, все свойства тела, которые связаны с энергией, такие как его ^{температура} или энергия связи систем, таких как ядра или молекулы , вносят вклад в массу этого тела и, следовательно, действуют как источники гравитации. ^[20]

В специальной теории относительности энергия тесно связана с импульсом . В специальной теории относительности, так же как пространство и время являются различными аспектами более всеобъемлющей сущности, называемой пространством-временем, энергия и импульс являются просто различными аспектами единой четырехмерной величины, которую физики называют четырехимпульсом . Следовательно, если энергия является источником гравитации, импульс также должен быть источником. То же самое верно для величин, которые напрямую связаны с энергией и импульсом, а именно внутреннего давления и натяжения . Взятые вместе, в общей теории относительности именно масса, энергия, импульс, давление и натяжение служат источниками гравитации: они являются тем, как материя сообщает пространству-времени, как искривляться. В математической формулировке теории все эти величины являются лишь аспектами более общей физической величины, называемой тензором энергии-импульса . ^[21]

Уравнения Эйнштейна являются центральным элементом общей теории относительности. Они дают точную формулировку взаимосвязи между геометрией пространства-времени и свойствами материи, используя язык математики. Более конкретно, они сформулированы с использованием концепций римановой геометрии , в которой геометрические свойства пространства (или пространства-времени) описываются величиной, называемой метрикой . Метрика кодирует информацию, необходимую для вычисления фундаментальных геометрических понятий расстояния и угла в искривленном пространстве (или пространстве-времени).

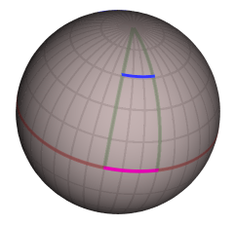
Сферическая поверхность, такая как у Земли, дает простой пример. Местоположение любой точки на поверхности можно описать двумя координатами: географической широтой и долготой . В отличие от декартовых координат плоскости, разности координат не совпадают с расстояниями на поверхности, как показано на диаграмме справа: для кого-то на экваторе перемещение на 30 градусов долготы на запад (пурпурная линия) соответствует расстоянию примерно в 3300 километров (2100 миль), в то время как для кого-то на широте 55 градусов перемещение на 30 градусов долготы на запад (синяя линия) покрывает расстояние всего в 1900 километров (1200 миль). Таким образом, координаты не предоставляют достаточно информации для описания геометрии сферической поверхности или геометрии любого более сложного пространства или пространства-времени. Именно эта информация закодирована в метрике, которая является функцией, определенной в каждой точке поверхности (или пространства, или пространства-времени) и связывает разности координат с разностями расстояния. Все другие величины, представляющие интерес в геометрии, такие как длина любой заданной кривой или угол, под которым встречаются две кривые, могут быть вычислены с помощью этой метрической функции. ^[22]

Метрическая функция и скорость ее изменения от точки к точке могут быть использованы для определения геометрической величины, называемой тензором кривизны Римана , которая точно описывает, как риманово многообразие , пространство-время в теории относительности, искривляется в каждой точке. Как уже упоминалось, материальное содержание пространства-времени определяет другую величину, тензор энергии-импульса T , и принцип, что «пространство-время говорит материи, как двигаться, а материя говорит пространству-времени, как искривляться», означает, что эти величины должны быть связаны друг с другом. Эйнштейн сформулировал это соотношение, используя тензор кривизны Римана и метрику, чтобы определить другую геометрическую величину G , теперь называемую тензором Эйнштейна , которая описывает некоторые аспекты искривления пространства-времени. Уравнение Эйнштейна затем утверждает, что

${\displaystyle \mathbf {G} ={\frac {8\pi G}{c^{4}}}\mathbf {T} ,}$

т.е. с точностью до постоянного кратного величина G (измеряющая кривизну) приравнивается к величине T (измеряющей содержание материи). Здесь G — гравитационная постоянная ньютоновской гравитации, а c — скорость света из специальной теории относительности.

Это уравнение часто называют во множественном числе уравнениями Эйнштейна , поскольку величины G и T определяются несколькими функциями координат пространства-времени, и уравнения уравнивают каждую из этих компонентных функций. ^[23] Решение этих уравнений описывает определенную геометрию пространства-времени ; например, решение Шварцшильда описывает геометрию вокруг сферической, невращающейся массы, такой как звезда или черная дыра , тогда как решение Керра описывает вращающуюся черную дыру. Другие решения могут описывать гравитационную волну или, в случае решения Фридмана-Леметра-Робертсона-Уокера , расширяющуюся вселенную. Простейшим решением является неискривленное пространство-время Минковского , пространство-время, описываемое специальной теорией относительности. ^[24]

Ни одна научная теория не является самоочевидно истинной; каждая представляет собой модель, которая должна быть проверена экспериментально. Закон тяготения Ньютона был принят, потому что он объяснял движение планет и лун в Солнечной системе со значительной точностью. По мере того, как точность экспериментальных измерений постепенно улучшалась, были обнаружены некоторые расхождения с предсказаниями Ньютона, и они были учтены в общей теории относительности. Аналогично, предсказания общей теории относительности также должны быть проверены экспериментально, и сам Эйнштейн разработал три теста, которые теперь известны как классические тесты теории:

• Ньютоновская гравитация предсказывает, что орбита , которую описывает одна планета вокруг идеально сферической звезды , должна быть эллипсом . Теория Эйнштейна предсказывает более сложную кривую: планета ведет себя так, как будто она движется по эллипсу, но в то же время эллипс в целом медленно вращается вокруг звезды. На диаграмме справа эллипс, предсказанный ньютоновской гравитацией, показан красным, а часть орбиты, предсказанной Эйнштейном, синим. Для планеты, вращающейся вокруг Солнца, это отклонение от орбит Ньютона известно как аномальное смещение перигелия . Первое измерение этого эффекта для планеты Меркурий датируется 1859 годом. Наиболее точные результаты для Меркурия и других планет на сегодняшний день основаны на измерениях, которые проводились между 1966 и 1990 годами с использованием радиотелескопов . ^[25] Общая теория относительности предсказывает правильное аномальное смещение перигелия для всех планет, где его можно точно измерить ( Меркурий , Венера и Земля).
• Согласно общей теории относительности, свет не распространяется по прямым линиям, когда распространяется в гравитационном поле. Вместо этого он отклоняется в присутствии массивных тел. В частности, звездный свет отклоняется, проходя вблизи Солнца, что приводит к кажущимся смещениям до 1,75 угловых секунд в положениях звезд на небе (угловая секунда равна 1/3600 градуса ) . В рамках ньютоновской гравитации можно сделать эвристический аргумент, который приводит к отклонению света на половину этой величины. Различные предсказания можно проверить, наблюдая звезды, которые находятся близко к Солнцу во время солнечного затмения . Таким образом, британская экспедиция в Западную Африку в 1919 году под руководством Артура Эддингтона подтвердила, что предсказание Эйнштейна было верным, а предсказания Ньютона — неверными, посредством наблюдения за затмением в мае 1919 года . Результаты Эддингтона были не очень точными; Последующие наблюдения отклонения света далеких квазаров Солнцем, в которых использовались высокоточные методы радиоастрономии , подтвердили результаты Эддингтона со значительно большей точностью (первые такие измерения датируются 1967 годом, последний всесторонний анализ — 2004 годом). ^[26]
• Гравитационное красное смещение было впервые измерено в лабораторных условиях в 1959 году Паундом и Ребкой . Оно также наблюдается в астрофизических измерениях, в частности, для света, покидающего белый карлик Сириус B. Связанный с этим эффект гравитационного замедления времени был измерен путем перемещения атомных часов на высоты от десятков до десятков тысяч километров (впервые Хафеле и Китинг в 1971 году; наиболее точно на сегодняшний день с помощью Gravity Probe A, запущенного в 1976 году). ^[27]

Из этих испытаний только смещение перигелия Меркурия было известно до окончательной публикации Эйнштейном общей теории относительности в 1916 году. Последующее экспериментальное подтверждение его других предсказаний, особенно первые измерения отклонения света Солнцем в 1919 году, вознесли Эйнштейна к международной славе. ^[28] Эти три эксперимента оправдали принятие общей теории относительности вместо теории Ньютона и, между прочим, вместо ряда альтернатив общей теории относительности , которые были предложены.

Дальнейшие тесты общей теории относительности включают точные измерения эффекта Шапиро или гравитационной задержки времени для света, измеренные в 2002 году космическим зондом Кассини . Один набор тестов фокусируется на эффектах, предсказанных общей теорией относительности для поведения гироскопов, путешествующих в космосе. Один из этих эффектов, геодезическая прецессия , был проверен с помощью эксперимента по лазерной локации Луны (высокоточные измерения орбиты Луны ) . Другой, который связан с вращающимися массами, называется увлечением кадра . Геодезические и увлекающие кадр эффекты были проверены спутниковым экспериментом Gravity Probe B , запущенным в 2004 году, с результатами, подтверждающими относительность с точностью до 0,5% и 15% соответственно по состоянию на декабрь 2008 года. ^[29]

По космическим меркам гравитация во всей Солнечной системе слаба. Поскольку различия между предсказаниями теорий Эйнштейна и Ньютона наиболее выражены, когда гравитация сильна, физики давно интересуются проверкой различных релятивистских эффектов в условиях сравнительно сильных гравитационных полей. Это стало возможным благодаря точным наблюдениям двойных пульсаров . В такой звездной системе две очень компактные нейтронные звезды вращаются друг вокруг друга. По крайней мере, одна из них является пульсаром  — астрономическим объектом, который испускает плотный пучок радиоволн. Эти лучи попадают на Землю с очень регулярными интервалами, подобно тому, как вращающийся луч маяка означает, что наблюдатель видит, как маяк мигает, и может наблюдаться как очень регулярная серия импульсов. Общая теория относительности предсказывает определенные отклонения от регулярности этих радиоимпульсов. Например, в моменты, когда радиоволны проходят близко к другой нейтронной звезде, они должны отклоняться гравитационным полем звезды. Наблюдаемые паттерны импульсов впечатляюще близки к тем, которые предсказывает общая теория относительности. ^[30]

Один конкретный набор наблюдений связан с чрезвычайно полезными практическими приложениями, а именно со спутниковыми навигационными системами , такими как Глобальная система позиционирования , которые используются как для точного позиционирования, так и для хронометража . Такие системы полагаются на два набора атомных часов : часы на борту спутников, вращающихся вокруг Земли, и эталонные часы, размещенные на поверхности Земли. Общая теория относительности предсказывает, что эти два набора часов должны идти с немного разной скоростью из-за их разных движений (эффект, уже предсказанный специальной теорией относительности) и их разных положений в гравитационном поле Земли. Чтобы обеспечить точность системы, либо спутниковые часы замедляются релятивистским фактором, либо этот же фактор становится частью алгоритма оценки. В свою очередь, тесты точности системы (особенно очень тщательные измерения, которые являются частью определения универсального координированного времени ) свидетельствуют о справедливости релятивистских предсказаний. ^[31]

Ряд других тестов проверяли справедливость различных версий принципа эквивалентности ; строго говоря, все измерения гравитационного замедления времени являются тестами слабой версии этого принципа , а не самой общей теории относительности. До сих пор общая теория относительности прошла все наблюдательные тесты. ^[32]

Модели, основанные на общей теории относительности, играют важную роль в астрофизике ; успех этих моделей является еще одним свидетельством справедливости теории.

Поскольку свет отклоняется в гравитационном поле, свет от удаленного объекта может достичь наблюдателя по двум или более путям. Например, свет от очень удаленного объекта, такого как квазар, может пройти по одной стороне массивной галактики и слегка отклониться, чтобы достичь наблюдателя на Земле, в то время как свет, проходящий по противоположной стороне той же галактики, также отклоняется, достигая того же наблюдателя с немного другого направления. В результате этот конкретный наблюдатель увидит один астрономический объект в двух разных местах ночного неба. Этот вид фокусировки хорошо известен, когда речь идет об оптических линзах , и, следовательно, соответствующий гравитационный эффект называется гравитационным линзированием . ^[33]

Наблюдательная астрономия использует эффекты линзирования как важный инструмент для вывода свойств линзирующего объекта. Даже в случаях, когда этот объект не виден напрямую, форма линзированного изображения дает информацию о распределении масс , ответственных за отклонение света. В частности, гравитационное линзирование дает один из способов измерения распределения темной материи , которая не испускает свет и может наблюдаться только по ее гравитационным эффектам. Одним из особенно интересных приложений являются крупномасштабные наблюдения, где линзирующие массы распределены по значительной части наблюдаемой Вселенной и могут использоваться для получения информации о крупномасштабных свойствах и эволюции нашего космоса. ^[34]

Гравитационные волны , прямое следствие теории Эйнштейна, являются искажениями геометрии, которые распространяются со скоростью света, и могут рассматриваться как рябь в пространстве-времени. Их не следует путать с гравитационными волнами гидродинамики , которые представляют собой другую концепцию.

В феврале 2016 года команда Advanced LIGO объявила, что они напрямую наблюдали гравитационные волны от слияния черных дыр . ^[35]

Косвенно, эффект гравитационных волн был обнаружен в наблюдениях за определенными двойными звездами. Такие пары звезд вращаются вокруг друг друга и, по мере того, как они это делают, постепенно теряют энергию, испуская гравитационные волны. Для обычных звезд, таких как Солнце, эта потеря энергии была бы слишком мала, чтобы ее можно было обнаружить, но эта потеря энергии была обнаружена в 1974 году в двойном пульсаре под названием PSR1913+16 . В такой системе одна из вращающихся звезд является пульсаром. Это имеет два последствия: пульсар является чрезвычайно плотным объектом, известным как нейтронная звезда , для которого излучение гравитационных волн намного сильнее, чем для обычных звезд. Кроме того, пульсар испускает узкий пучок электромагнитного излучения из своих магнитных полюсов. Когда пульсар вращается, его луч проносится над Землей, где он виден как регулярная серия радиоимпульсов, так же как корабль в море наблюдает регулярные вспышки света от вращающегося света на маяке. Этот регулярный узор радиоимпульсов функционирует как высокоточные «часы». Его можно использовать для измерения орбитального периода двойной звезды, и он чутко реагирует на искажения пространства-времени в непосредственной близости от него.

Первооткрыватели PSR1913+16, Рассел Халс и Джозеф Тейлор , были удостоены Нобелевской премии по физике в 1993 году. С тех пор было обнаружено несколько других двойных пульсаров. Наиболее полезными являются те, в которых обе звезды являются пульсарами, поскольку они обеспечивают точные проверки общей теории относительности. ^[36]

В настоящее время работает ряд наземных детекторов гравитационных волн , а также разрабатывается миссия по запуску космического детектора LISA , предшествовавшая миссия ( LISA Pathfinder ), которая была запущена в 2015 году. Наблюдения за гравитационными волнами могут быть использованы для получения информации о компактных объектах, таких как нейтронные звезды и черные дыры, а также для исследования состояния ранней Вселенной через доли секунды после Большого взрыва . ^[37]

Когда масса концентрируется в достаточно компактной области пространства, общая теория относительности предсказывает образование черной дыры  — области пространства с гравитационным эффектом настолько сильным, что даже свет не может вырваться из нее. Определенные типы черных дыр считаются конечным состоянием в эволюции массивных звезд . С другой стороны, сверхмассивные черные дыры с массой в миллионы или миллиарды Солнц , как предполагается, находятся в ядрах большинства галактик , и они играют ключевую роль в современных моделях того, как галактики формировались за последние миллиарды лет. ^[38]

Падение материи на компактный объект является одним из наиболее эффективных механизмов высвобождения энергии в форме излучения , и считается, что падение материи на черные дыры ответственно за некоторые из самых ярких астрономических явлений, которые только можно себе представить. Известными примерами, представляющими большой интерес для астрономов, являются квазары и другие типы активных галактических ядер . При правильных условиях падающая материя, накапливающаяся вокруг черной дыры, может привести к образованию струй , в которых сфокусированные пучки материи выбрасываются в космос со скоростью, близкой к скорости света . ^[39]

Есть несколько свойств, которые делают черные дыры наиболее перспективными источниками гравитационных волн. Одна из причин заключается в том, что черные дыры являются наиболее компактными объектами, которые могут вращаться вокруг друг друга как часть двойной системы; в результате гравитационные волны, испускаемые такой системой, особенно сильны. Другая причина вытекает из так называемых теорем уникальности черных дыр : со временем черные дыры сохраняют только минимальный набор отличительных черт (эти теоремы стали известны как теоремы «без волос»), независимо от начальной геометрической формы. Например, в долгосрочной перспективе коллапс гипотетического куба материи не приведет к образованию черной дыры в форме куба. Вместо этого полученная черная дыра будет неотличима от черной дыры, образованной коллапсом сферической массы. При переходе к сферической форме черная дыра, образованная коллапсом более сложной формы, будет испускать гравитационные волны. ^[40]

Одним из важнейших аспектов общей теории относительности является то, что она может быть применена ко Вселенной в целом. Ключевым моментом является то, что в больших масштабах наша Вселенная, по-видимому, построена по очень простым линиям: все текущие наблюдения показывают, что в среднем структура космоса должна быть примерно одинаковой, независимо от местоположения наблюдателя или направления наблюдения: Вселенная приблизительно однородна и изотропна . Такие сравнительно простые вселенные могут быть описаны простыми решениями уравнений Эйнштейна. Современные космологические модели Вселенной получены путем объединения этих простых решений общей теории относительности с теориями, описывающими свойства материи , содержащейся во Вселенной, а именно термодинамикой , ядерной физикой и физикой элементарных частиц . Согласно этим моделям, наша нынешняя Вселенная возникла из чрезвычайно плотного высокотемпературного состояния — Большого взрыва  — примерно 14 миллиардов лет назад и с тех пор расширяется. [ ^41]

Уравнения Эйнштейна можно обобщить, добавив член, называемый космологической постоянной . Когда этот член присутствует, пустое пространство само по себе действует как источник притягивающей (или, реже, отталкивающей) гравитации. Эйнштейн первоначально ввел этот термин в своей пионерской статье 1917 года по космологии с очень конкретной мотивацией: современная космологическая мысль считала вселенную статичной, и дополнительный член требовался для построения статических моделей вселенных в рамках общей теории относительности. Когда стало очевидно, что вселенная не статична, а расширяется, Эйнштейн быстро отказался от этого дополнительного члена. Однако с конца 1990-х годов астрономические свидетельства, указывающие на ускоряющееся расширение, согласующееся с космологической постоянной — или, что эквивалентно, с определенным и вездесущим видом темной энергии  — неуклонно накапливались. ^[42]

Общая теория относительности очень успешно обеспечивает основу для точных моделей, которые описывают впечатляющий набор физических явлений. С другой стороны, есть много интересных открытых вопросов, и в частности, теория в целом почти наверняка неполна. ^[43]

В отличие от всех других современных теорий фундаментальных взаимодействий , общая теория относительности является классической теорией: она не включает эффекты квантовой физики . Поиск квантовой версии общей теории относительности затрагивает один из самых фундаментальных открытых вопросов в физике. Хотя есть многообещающие кандидаты на такую ​​теорию квантовой гравитации , в частности, теория струн и петлевая квантовая гравитация , в настоящее время не существует последовательной и полной теории. Долгое время надеялись, что теория квантовой гравитации также устранит другую проблемную особенность общей теории относительности: наличие сингулярностей пространства-времени . Эти сингулярности являются границами («острыми краями») пространства-времени, на которых геометрия становится плохо определенной, в результате чего сама общая теория относительности теряет свою предсказательную силу. Кроме того, существуют так называемые теоремы о сингулярностях , которые предсказывают, что такие сингулярности должны существовать во Вселенной, если законы общей теории относительности должны соблюдаться без каких-либо квантовых модификаций. Наиболее известными примерами являются сингулярности, связанные с модельными вселенными, которые описывают черные дыры и начало Вселенной . ^[44]

Другие попытки модифицировать общую теорию относительности были сделаны в контексте космологии . В современных космологических моделях большая часть энергии во Вселенной находится в формах, которые никогда не были обнаружены напрямую, а именно темная энергия и темная материя . Было несколько спорных предложений по устранению необходимости в этих загадочных формах материи и энергии путем изменения законов, управляющих гравитацией и динамикой космического расширения , например, модифицированной ньютоновской динамики . ^[45]

Помимо проблем квантовых эффектов и космологии, исследования общей теории относительности богаты возможностями для дальнейшего изучения: специалисты по математическому релятивизму изучают природу сингулярностей и фундаментальные свойства уравнений Эйнштейна ^[46] , и проводятся все более полные компьютерные моделирования конкретных пространств-времен (например, описывающих слияние черных дыр). ^[47] Более чем через сто лет после первой публикации теории исследования стали более активными, чем когда-либо. ^[48]

В Wikibooks есть книга по теме: Общая теория относительности

На Викискладе есть медиафайлы по теме Общая теория относительности .

Послушайте эту статью ( 49 минут )

Этот аудиофайл был создан на основе редакции этой статьи от 9 мая 2021 года и не отражает последующие правки. (2021-05-09)

( Аудиопомощь  · Больше устных статей )

Дополнительные ресурсы, включая более продвинутый материал, можно найти в разделе « Ресурсы по общей теории относительности» .

• Einstein Online. Сайт, на котором представлены статьи по различным аспектам релятивистской физики для широкой аудитории, размещенный в Институте гравитационной физики Макса Планка.
• NCSA Spacetime Wrinkles. Веб-сайт, созданный группой численной теории относительности в Национальном центре суперкомпьютерных приложений , содержащий элементарное введение в общую теорию относительности, черные дыры и гравитационные волны.