Узловой анализ

В анализе электрических цепей узловой анализ , анализ узлового напряжения или метод токов ветвей — это метод определения напряжения ( разности потенциалов ) между « узлами » (точками соединения элементов или ветвей) в электрической цепи через токи ветвей.

Узловой анализ по сути является систематическим применением закона токов Кирхгофа (KCL) для анализа цепей . Аналогично, анализ сетки является систематическим применением закона напряжений Кирхгофа (KVL). Узловой анализ записывает уравнение в каждом электрическом узле, определяющее, что токи ветвей, падающие на узел, должны быть в сумме равны нулю (с использованием KCL). Токи ветвей записываются в терминах напряжений узлов цепи. Как следствие, каждое определяющее соотношение ветвей должно давать ток как функцию напряжения; представление проводимости . Например, для резистора I _ветвь = V _ветвь * G, где G (=1/R) — проводимость (кондуктивность) резистора.

Узловой анализ возможен, когда все звенья определяющих отношений элементов схемы имеют представление проводимости. Узловой анализ создает компактный набор уравнений для сети, который может быть решен вручную, если он небольшой, или может быть быстро решен с помощью линейной алгебры на компьютере. Из-за компактной системы уравнений многие программы моделирования схем (например, SPICE ) используют узловой анализ в качестве основы. Когда элементы не имеют представления проводимости, можно использовать более общее расширение узлового анализа, модифицированный узловой анализ .

1. Обратите внимание на все подключенные сегменты проводов в схеме. Это узлы узлового анализа.
2. Выберите один узел в качестве опорного заземления . Выбор не влияет на напряжения элементов (но влияет на узловые напряжения) и является просто вопросом соглашения. Выбор узла с наибольшим количеством соединений может упростить анализ. Для схемы из N узлов число узловых уравнений равно N −1.
3. Назначьте переменную для каждого узла, напряжение которого неизвестно. Если напряжение уже известно, то нет необходимости назначать переменную.
4. Для каждого неизвестного напряжения составьте уравнение на основе закона токов Кирхгофа (т.е. сложите все токи, выходящие из узла, и приравняйте сумму к нулю). Ток между двумя узлами равен напряжению узла, из которого ток выходит, за вычетом напряжения узла, из которого ток входит в узел, деленного на сопротивление между двумя узлами.
5. Если между двумя неизвестными напряжениями есть источники напряжения, объедините два узла в суперузел . Токи двух узлов объединяются в одно уравнение, и формируется новое уравнение для напряжений.
6. Решите систему уравнений для каждого неизвестного напряжения.

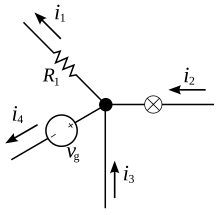
Единственное неизвестное напряжение в этой цепи равно . К этому узлу есть три соединения и, следовательно, три тока, которые следует учитывать. Направление токов в расчетах выбрано от узла.${\displaystyle V_{1}}$

1. Ток через резистор :${\displaystyle R_{1}}$${\displaystyle (V_{1}-V_{S})/R_{1}}$
2. Ток через резистор :${\displaystyle R_{2}}$${\displaystyle V_{1}/R_{2}}$
3. Ток через источник тока :${\displaystyle I_{S}}$${\displaystyle -I_{S}}$

Используя закон Кирхгофа, получаем:

$${\displaystyle {\frac {V_{1}-V_{S}}{R_{1}}}+{\frac {V_{1}}{R_{2}}}-I_{S}=0}$$

Это уравнение можно решить относительно V ₁ :

$${\displaystyle V_{1}={\frac {\left({\frac {V_{S}}{R_{1}}}+I_{S}\right)}{\left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)}}}$$

Наконец, неизвестное напряжение можно решить, подставив числовые значения вместо символов. Любые неизвестные токи легко вычислить, когда все напряжения в цепи известны.

$${\displaystyle V_{1}={\frac {\left({\frac {5{\text{ V}}}{100\,\Omega }}+20{\text{ мА}}\right)}{\left({\frac {1}{100\,\Omega }}+{\frac {1}{200\,\Omega }}\right)}}={\frac {14}{3}}{\text{ V}}}$$

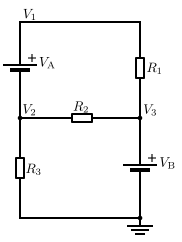
В этой схеме изначально имеются два неизвестных напряжения, V ₁ и V _2. Напряжение на V ₃ уже известно как V _B, поскольку другой вывод источника напряжения находится под потенциалом земли.

Ток, проходящий через источник напряжения V _{A ,} не может быть напрямую рассчитан. Поэтому мы не можем написать уравнения тока для V ₁ или V ₂ . Однако мы знаем, что тот же ток, выходящий из узла V _{2 ,} должен войти в узел V ₁ . Несмотря на то, что узлы не могут быть решены по отдельности, мы знаем, что объединенный ток этих двух узлов равен нулю. Такое объединение двух узлов называется методом суперузла , и оно требует одного дополнительного уравнения: V ₁ = V ₂ + V _A .

Полный набор уравнений для этой схемы:

$${\displaystyle {\begin{cases}{\frac {V_{1}-V_{\text{B}}}{R_{1}}}+{\frac {V_{2}-V_{\text{B }}}{R_{2}}}+{\frac {V_{2}}{R_{3}}}=0\\V_{1}=V_{2}+V_{\text{A}}\\\end{cases}}}$$

Заменяя$${\displaystyle V_{2}={\frac {(R_{1}+R_{2})R_{3}V_{\text{B}}-R_{2}R_{3}V_{\text{A}}}{(R_{1}+R_{2})R_{3}+R_{1}R_{2}}}}$$

В общем случае для схемы с узлами уравнения узлового напряжения, полученные с помощью узлового анализа, можно записать в матричной форме, как выведено ниже. Для любого узла KCL устанавливает , где — отрицательная сумма проводимостей между узлами и , а — напряжение узла . Это подразумевает, где — сумма проводимостей, подключенных к узлу . Отметим, что первый член вносит линейное вклад в узел через , в то время как второй член вносит линейное вклад в каждый узел, подключенный к узлу через со знаком минус. Если независимый источник тока/вход также подключен к узлу , приведенное выше выражение обобщается до . Легко показать, что можно объединить приведенные выше уравнения узлового напряжения для всех узлов и записать их в следующей матричной форме${\displaystyle N}$${\displaystyle к}$${\textstyle \sum _{j\neq k}G_{jk}(v_{k}-v_{j})=0}$${\displaystyle G_{kj}=G_{jk}}$${\displaystyle к}$${\displaystyle j}$${\displaystyle v_{k}}$${\displaystyle к}$${\textstyle 0 =\sum _{j\neq k}G_{jk}(v_{k}-v_{j})=\sum _{j\neq k}G_{jk}v_{k}-\sum _{j\neq k}G_{jk}v_{j}=G_{kk}v_{k}-\sum _{j\neq k}G_{jk}v_{j}}$${\displaystyle G_{kk}}$${\displaystyle к}$${\displaystyle к}$${\displaystyle G_{kk}}$${\displaystyle j}$${\displaystyle к}$${\displaystyle G_{jk}}$${\displaystyle i_{k}}$${\displaystyle к}$${\textstyle i_{k}=G_{kk}v_{k}-\sum _{j\neq k}G_{jk}v_{j}}$${\displaystyle N}$

$${\displaystyle {\begin{pmatrix}G_{11}&G_{12}&\cdots &G_{1N}\\G_{21}&G_{22}&\cdots &G_{2N}\\\vdots &\vdots &\ddots &\vdots \\G_{N1}&G_{N2}&\cdots &G_{NN}\end{pmatrix}}{\begin{pmatrix}v_{1}\\v_{2}\\\vdots \\v_{N}\end{pmatrix}}={\begin{pmatrix}i_{1}\\i_{2}\\\vdots \\i_{N}\end{pmatrix}}}$$или просто${\textstyle \mathbf {Gv} =\mathbf {i} .}$

Матрица в левой части уравнения является сингулярной, поскольку она удовлетворяет , где — матрица столбцов, содержащая только единицы. Это соответствует факту сохранения тока, а именно, , и свободе выбора опорного узла (земли). На практике напряжение в опорном узле принимается равным 0. Предположим, что это последний узел, . В этом случае легко проверить, что полученные уравнения для других узлов остаются прежними, и поэтому можно просто отбросить последний столбец, а также последнюю строку матричного уравнения. Эта процедура приводит к размерному несингулярному матричному уравнению, в котором определения всех элементов остаются неизменными.${\displaystyle \mathbf {G} }$${\displaystyle \mathbf {G1} =0}$${\displaystyle \mathbf {1} }$${\displaystyle N\times 1}$${\textstyle \sum _{k}i_{k}=0}$${\displaystyle v_{N}=0}$${\displaystyle N-1}$${\displaystyle (N-1)\times (N-1)}$

• Анализ сетки
• Ybus-матрица
• Топология (электрические цепи)
• Сохранение заряда
• Схема цепи

• П. Димо Узловой анализ энергосистем Abacus Press Kent 1975

Викиверситет содержит обучающие ресурсы по узловому анализу

• Метод ветвления тока
• Онлайн-решение четырехузловых задач
• Пример простого узлового анализа