Список систем счисления

В этой статье содержатся необычные символы Unicode . Без надлежащей поддержки рендеринга вы можете увидеть вопросительные знаки, квадраты или другие символы вместо предполагаемых символов.

Существует множество различных систем счисления , то есть систем письма для выражения чисел .

« Основание — это натуральное число B, степени которого (B, умноженное само на себя некоторое количество раз) специально обозначены в числовой системе». ^{[1] : 38} Этот термин не эквивалентен основанию , поскольку он применяется ко всем числовым системам записи (не только к позиционным с основанием) и большинству систем устных чисел. ^[1] Некоторые системы имеют два основания, меньшее (подоснование) и большее (основание); примером являются римские цифры, которые организованы по пятеркам (V=5, L=50, D=500, подоснование) и десяткам (X=10, C=100, M=1000, основание).

Имя	База	Образец	Приблизительное первое появление
Протоклинописные цифры	10 и 60		ок. 3500–2000 до н.э.
Индийские цифры			ок. 3500–1900 до н.э.
Протоэламские цифры	10 и 60		3100 г. до н.э.
Шумерские цифры	10 и 60		3100 г. до н.э.
египетские цифры	10		3000 г. до н.э.
Вавилонские цифры	10 и 60		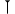2000 г. до н.э.
Эгейские цифры	10	𐄇 𐄈 𐄉 𐄊 𐄋 𐄌 𐄍 𐄎 𐄏 ( 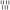) 𐄐 𐄑 𐄒 𐄓 𐄔 𐄕 𐄖 𐄗 𐄘 ( ) 𐄙 𐄚 𐄛 𐄜 𐄝 𐄞 𐄟 𐄠 𐄡 ( 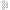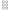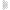) 𐄢 𐄣 𐄤 𐄥 𐄦 𐄧 𐄨 𐄩 𐄪 ( ) 𐄫 𐄬 𐄭 𐄮 𐄯 𐄰 𐄱 𐄲 𐄳 ( )	1500 г. до н.э.
Китайские цифры Японские цифры Корейские цифры ( китайско-корейские ) Вьетнамские цифры ( китайско-вьетнамские )	10	零一二三四五六七八九十百千萬億 (по умолчанию, традиционный китайский ) 〇一二三四五六七八九十百千万亿 (по умолчанию, упрощенный китайский )	1300 г. до н.э.
римские цифры	5 и 10	IVXLCDM	1000 г. до н.э. [1]
Еврейские цифры	10	א ב ג ד ה ו ז ח ט י כ ל מ נ ס ע פ צ ק ר ש ת ך ם ן ף ץ	800 г. до н.э.
Индийские цифры	10	Бенгальский ০ ১ ২ ৩ ৪ ৫ ৬ ৭ ৮ ৯ Деванагари ० १ २ ३ ४ ५ ६ ७ ८ ९ Гуджарати ૦ ૧ ૨ ૩ ૪ ૫ ૬ ૭ ૮ ૯ Каннада ೦ ೧ ೨ ೩ ೪ ೫ ೬ ೭ ೮ ೯ Малаялам ൦ ൧ ൨ ൩ ൪ ൫ ൬ ൭ ൮ ൯ Одиа ୦ ୧ ୨ ୩ ୪ ୫ ୬ ୭ ୮ ୯ Пенджаби ੦ ੧ ੨ ੩ ੪ ੫ ੬ ੭ ੮ ੯ Тамил ௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯ Телугу ౦ ౧ ౨ ౩ ౪ ౫ ౬ ౭ ౮ ౯ Тибетский ༠ ༡ ༢ ༣ ༤ ༥ ༦ ༧ ༨ ༩ Урду ۰ ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹	750–500 до н.э.
Греческие цифры	10	ō α β γ δ ε ϝ ζ η θ ι ο Α' Β' Γ' Δ' Ε' Ϛ' Ζ' Η' Θ'	<400 г. до н.э.
Цифры кхароштхи	4 и 10	𐩇 𐩆 𐩅 𐩄 𐩃 𐩂 𐩁 𐩀	<400–250 до н.э. [2]
Финикийские цифры	10	𐤙 𐤘 𐤗 𐤛𐤛𐤛 𐤛𐤛𐤚 𐤛𐤛𐤖 𐤛𐤛 𐤛𐤚 𐤛𐤖 𐤛 𐤚 𐤖 [3]	<250 г. до н.э. [4]
Китайские стержневые цифры	10	𝍠 𝍡 𝍢 𝍣 𝍤 𝍥 𝍦 𝍧 𝍨 𝍩	1-й век
Коптские цифры	10	Ⲁ Ⲃ Ⲅ Ⲇ Ⲉ Ⲋ Ⲍ Ⲏ Ⲑ	2-й век
Цифры на языке геэз	10	፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ ፻ ፼ [5]	3–4 век 15 век (современный стиль) [6]
Армянские цифры	10	Ա Բ Գ Դ Ե Զ Է Ը Թ Ժ	Начало V века
Кхмерские цифры	10	០ ១ ២ ៣ ៤ ៥ ៦ ៧ ៨ ៩	Начало VII века
тайские цифры	10	๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙	7 век [7]
Числа Абджад	10	غ ظ ض ذ خ ث ت ش ر ق ص ف ع س ن م ل ك ي ط ح ز و هـ د ج ب ا	<8 век
Китайские цифры (финансовые)	10	零壹貳參肆伍陸柒捌玖拾佰仟萬億 (тихоокеанский китайский) 零壹贰叁肆伍陆柒捌玖拾佰仟萬億 (южнокитайский)	конец 7-го/начало 8-го века [8]
Восточно-арабские цифры	10	٩ ٨ ٧ ٦ 5 4 ...	8 век
Вьетнамские цифры ( Chữ Nôm )	10	𠬠 𠄩 𠀧 𦊚 𠄼 𦒹 𦉱 𠔭 𠃩	<9 век
Западные арабские цифры	10	0 1 2 3 4 5 6 7 8 9	9 век
Глаголические числительные	10	Ⰰ Ⰱ Ⰲ Ⰳ Ⰴ Ⰵ Ⰶ Ⰷ Ⰸ ...	9 век
Кириллические цифры	10	а в г д е е з и й...	10 век
Цифры Руми	10		10 век
Бирманские цифры	10	၀ ၁ ၂ ၃ ၄ ၅ ၆ ၇ ၈ ၉	11 век [9]
Тангутские числительные	10	𘈩 𗍫 𘕕 𗥃 𗏁 𗤁 𗒹 𘉋 𗢭 𗰗	11 век (1036)
Цистерцианские цифры	10		13 век
Цифры майя	5 и 20		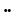<15 век
Числа Муиска	20		<15 век
Корейские цифры ( хангыль )	10	영 일 이 삼 사 오 육 칠 팔 구	15 век (1443)
Ацтекские цифры	20		16 век
Сингальские цифры	10	෦ ෧ ෨ ෩ ෪ ෫ ෬ ෭ ෮ ෯ 𑇡 𑇢 𑇣 𑇤 𑇥 𑇦 𑇧 𑇨 𑇩 𑇪 𑇫 𑇬 𑇭 𑇮 𑇯 𑇰 𑇱 𑇲 𑇳 𑇴	<18 век
Пентадические руны	10		19 век
Цифры чероки	10		19 век (1820-е годы)
Цифры Vai	10	꘠ ꘡ ꘢ ꘣ ꘤ ꘥ ꘦ ꘧ ꘨ ꘩ [10]	19 век (1832) [11]
Цифры Бамум	10	ꛯ ꛦ ꛧ ꛨ ꛩ ꛪ ꛫ ꛬ ꛭ ꛮ [12]	19 век (1896) [11]
Числа Менде Кикакуи	10	𞣏 𞣎 𞣍 𞣌 𞣋 𞣊 𞣉 𞣈 𞣇 [13]	20 век (1917) [14]
Османские цифры	10	𐒠 𐒡 𐒢 𐒣 𐒤 𐒥 𐒦 𐒧 𐒨 𐒩	20 век (1920-е годы)
Медефаидрин цифры	20	𖺀 𖺁/𖺔 𖺂/𖺕 𖺃/𖺖 𖺄 𖺅 𖺆 𖺇 𖺈 𖺉 𖺊 𖺋 𖺌 𖺍 𖺎 𖺏 𖺐 𖺑 𖺒 𖺓 [15]	20 век (1930-е годы) [16]
Цифры Н'Ко	10	ü​	20 век (1949) [18]
Числительные на языке хмонг	10	𖭐 𖭑 𖭒 𖭓 𖭔 𖭕 𖭖 𖭗 𖭘 𖭑𖭐	20 век (1959)
Цифры Гарая	10	[19]	20 век (1961) [20]
Цифры Адлама	10	𞥙 𞥘 𞥗 𞥖 𞥕 𞥔 𞥓 𞥒 𞥑 𞥐 [21]	20 век (1989) [22]
Кактовик цифры	5 и 20	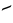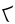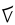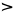𝋀 𝋁 𝋂 𝋃 𝋄 𝋅 𝋆 𝋇 𝋈 𝋉 𝋊 𝋋 𝋌 𝋍 𝋎 𝋏 𝋐 𝋑 𝋒 𝋓 [23]	20 век (1994) [24]
Суданские цифры	10	᮰ ᮱ ᮲ ᮳ ᮴ ᮵ ᮶ ᮷ ᮸ ᮹	20 век (1996) [25]

Системы счисления классифицируются здесь в зависимости от того, используют ли они позиционную систему счисления (также известную как разрядная система счисления), а также по основанию .

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (April 2023) (Learn how and when to remove this message)

Распространенные названия получены несколько произвольно из смеси латинского и греческого , в некоторых случаях включая корни из обоих языков в одном названии. ^[26] Были некоторые предложения по стандартизации. ^[27]

База	Имя	Использование
2 я	Кватер-мнимая база	относительно основания −4 и основания 16
${\displaystyle i{\sqrt {2}}}$	База${\displaystyle i{\sqrt {2}}}$	относительно основания −2 и основания 4
${\displaystyle i{\sqrt[{4}]{2}}}$	База${\displaystyle i{\sqrt[{4}]{2}}}$	связанный с базой 2
${\displaystyle 2\omega }$	База${\displaystyle 2\omega }$	связанный с основанием 8
${\displaystyle \omega {\sqrt[{3}]{2}}}$	База${\displaystyle \omega {\sqrt[{3}]{2}}}$	связанный с базой 2
−1 ± я	База Твиндрагона	Фрактальная форма Twindragon , связанная с основанием −4 и основанием 16
1 ± я	База Негатвиндрагона	относительно основания −4 и основания 16

База	Имя	Использование
${\displaystyle {\frac {3}{2}}}$	База${\displaystyle {\frac {3}{2}}}$	рациональное нецелое основание
${\displaystyle {\frac {4}{3}}}$	База${\displaystyle {\frac {4}{3}}}$	относящийся к двенадцатеричной системе
${\displaystyle {\frac {5}{2}}}$	База${\displaystyle {\frac {5}{2}}}$	относящийся к десятичному
${\displaystyle {\sqrt {2}}}$	База${\displaystyle {\sqrt {2}}}$	связанный с базой 2
${\displaystyle {\sqrt {3}}}$	База${\displaystyle {\sqrt {3}}}$	связанный с основанием 3
${\displaystyle {\sqrt[{3}]{2}}}$	База${\displaystyle {\sqrt[{3}]{2}}}$
${\displaystyle {\sqrt[{4}]{2}}}$	База${\displaystyle {\sqrt[{4}]{2}}}$
${\displaystyle {\sqrt[{12}]{2}}}$	База${\displaystyle {\sqrt[{12}]{2}}}$	использование в 12-тоновой равномерно темперированной музыкальной системе
${\displaystyle 2{\sqrt {2}}}$	База${\displaystyle 2{\sqrt {2}}}$
${\displaystyle -{\frac {3}{2}}}$	База${\displaystyle -{\frac {3}{2}}}$	отрицательное рациональное нецелое основание
${\displaystyle -{\sqrt {2}}}$	База${\displaystyle -{\sqrt {2}}}$	отрицательное нецелое основание, связанное с основанием 2
${\displaystyle {\sqrt {10}}}$	База${\displaystyle {\sqrt {10}}}$	относящийся к десятичному
${\displaystyle 2{\sqrt {3}}}$	База${\displaystyle 2{\sqrt {3}}}$	относящийся к двенадцатеричной системе
φ	Золотое сечение основа	ранний бета-кодер [66]
ρ	Пластиковая основа для цифр
ψ	База суперзолотого сечения
${\displaystyle 1+{\sqrt {2}}}$	База серебряного коэффициента
е	База${\displaystyle e}$	лучшая экономика счисления [ требуется ссылка ]
π	База${\displaystyle \pi }$
е π	База${\displaystyle e\pi }$
${\displaystyle e^{\pi }}$	База${\displaystyle e^{\pi }}$

• Факториальная система счисления {1, 2, 3, 4, 5, 6, ...}
• Чётная система счисления с двойным факториалом {2, 4, 6, 8, 10, 12, ...}
• Нечетная двухфакторная система счисления {1, 3, 5, 7, 9, 11, ...}
• Первичная система счисления {2, 3, 5, 7, 11, 13, ...}
• Фибоначчиская система счисления {1, 2, 3, 5, 8, 13, ...}
• {60, 60, 24, 7} в хронометраже
• {60, 60, 24, 30 (или 31 или 28 или 29), 12, 10, 10, 10} в хронометраже
• (12, 20) традиционная английская денежная система (£sd)
• (20, 18, 13) Летоисчисление майя

• Обозначение цитаты
• Избыточное двоичное представление
• Наследственная нотация с основанием n
• Асимметричные системы счисления , оптимизированные для неравномерного распределения вероятностей символов
• Комбинаторная система счисления

Все известные системы счисления, разработанные до вавилонских цифр, являются непозиционными, ^[67] как и многие из разработанных позже, такие как римские цифры . Французские монахи-цистерцианцы создали свою собственную систему счисления.