Эксцентрическая аномалия

В орбитальной механике эксцентрическая аномалия — это угловой параметр , определяющий положение тела, движущегося по эллиптической кеплеровской орбите . Эксцентрическая аномалия — это один из трех угловых параметров («аномалий»), определяющих положение по орбите, два других — это истинная аномалия и средняя аномалия .

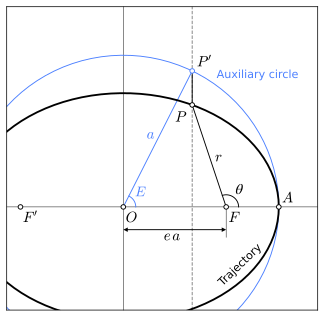
Рассмотрим эллипс с уравнением:

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,}$

где a — большая полуось , b — малая полуось .

Для точки на эллипсе, P  =  P ( x ,  y ), представляющей положение вращающегося тела на эллиптической орбите, эксцентрическая аномалия - это угол E на рисунке. Эксцентрическая аномалия E - это один из углов прямоугольного треугольника с одной вершиной в центре эллипса, его смежная сторона лежит на большой оси, имеет гипотенузу a (равную большой полуоси эллипса) и противолежащую сторону (перпендикулярную большой оси и касающуюся точки P′ на вспомогательной окружности радиуса a ), которая проходит через точку P . Эксцентрическая аномалия измеряется в том же направлении, что и истинная аномалия, показанная на рисунке как . Эксцентрическая аномалия E в терминах этих координат определяется как: ^[1]${\displaystyle \тета}$

${\displaystyle \cos E={\frac {x}{a}},}$

и

${\displaystyle \sin E={\frac {y}{b}}}$

Второе уравнение устанавливается с использованием соотношения

${\displaystyle \left({\frac {y}{b}}\right)^{2}=1-\cos ^{2}E=\sin ^{2}E}$,

что подразумевает, что sin E = ± ⁠у/б⁠ . Уравнение sin E = − ⁠у/б⁠ можно сразу исключить, так как он пересекает эллипс в неправильном направлении. Можно также отметить, что второе уравнение можно рассматривать как исходящее из подобного треугольника, у которого противоположная сторона имеет ту же длину y, что и расстояние от P до большой оси, а ее гипотенуза b равна малой полуоси эллипса.

Эксцентриситет e определяется как:

${\displaystyle e={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}\ .}$

Из теоремы Пифагора, примененной к треугольнику с r (расстояние FP ) в качестве гипотенузы:

${\displaystyle {\begin{align}r^{2}&=b^{2}\sin ^{2}E+(ae-a\cos E)^{2}\\&=a^{2}\left(1-e^{2}\right)\left(1-\cos ^{2}E\right)+a^{2}\left(e^{2}-2e\cos E+\cos ^{2}E\right)\\&=a^{2}-2a^{2}e\cos E+a^{2}e^{2}\cos ^{2}E\\&=a^{2}\left(1-e\cos E\right)^{2}\\\end{align}}}$

Таким образом, радиус (расстояние от фокуса до точки P ) связан с эксцентрической аномалией формулой

${\displaystyle r=a\left(1-e\cos {E}\right)\ .}$

С помощью этого результата эксцентрическая аномалия может быть определена из истинной аномалии, как показано далее.

Истинная аномалия — это угол, обозначенный на рисунке, расположенный в фокусе эллипса. Иногда он обозначается как f или v . Истинная аномалия и эксцентрическая аномалия связаны следующим образом. ^[2]${\displaystyle \тета}$

Используя формулу для r выше, синус и косинус E находятся через f  :

${\displaystyle {\begin{aligned}\cos E&={\frac {\,x\,}{a}}={\frac {\,ae+r\cos f\,}{a}}=e+( 1-e\cos E)\cos f\\\Rightarrow \cos E&={\frac {\,e+\cos f\,}{1+e\cos f}}\\\sin E&={\sqrt {\,1-\cos ^{2}E\;}}={\frac {\,{\sqrt {\,1-e^{2}\;}}\,\sin f \,}{1+e\cos f}}~.\end{aligned}}}$

Следовательно,

${\displaystyle \tan E={\frac {\,\sin E\,}{\cos E}}={\frac {\,{\sqrt {\,1-e^{2}\;}}\ ,\sin f\,}{e+\cos f}}~.}$

где правильный квадрант для E задается знаками числителя и знаменателя, так что E проще всего найти с помощью функции atan2 .

Угол E , следовательно, является смежным углом прямоугольного треугольника с гипотенузой, прилежащей стороной и противолежащей стороной.${\displaystyle \;1+e\cos f\;,}$${\displaystyle \;e+\cos f\;,}$${\displaystyle \;{\sqrt {\,1-e^{2}\;}}\,\sin f\;.}$

Также,

${\displaystyle \tan {\frac {\,f\,}{2}}={\sqrt {{\frac {\,1+e\,}{1-e}}\,}}\,\tan {\frac {\,E\,}{2}}}$

Подставляя cos  E , найденный выше, в выражение для r , можно также найти радиальное расстояние от фокальной точки до точки P через истинную аномалию: ^[2]

${\displaystyle r={\frac {a\left(\,1-e^{2}\,\right)}{\,1+e\cos f\,}}={\frac {p}{\,1+e\cos f\,}}\,}$

где

${\displaystyle \,p\equiv a\left(\,1-e^{2}\,\right)}$

в классической геометрии называется «полуширокая прямая кишка» .

Эксцентрическая аномалия E связана со средней аномалией M уравнением Кеплера : ^[3]

${\displaystyle M=E-e\sin E}$

Это уравнение не имеет замкнутого решения для E при заданном M. Обычно оно решается численными методами , например, методом Ньютона–Рафсона . Оно может быть выражено в ряду Фурье как

${\displaystyle E=M+2\sum _{n=1}^{\infty }{\frac {J_{n}(ne)}{n}}\sin(nM)}$

где — функция Бесселя первого рода.${\displaystyle J_{n}(x)}$

• Вектор эксцентриситета
• Эксцентриситет орбиты

• Мюррей, Карл Д.; и Дермотт, Стэнли Ф. (1999); Динамика солнечной системы , Cambridge University Press, Кембридж, Великобритания
• Пламмер, Генри К.К. (1960); Вводный трактат по динамической астрономии , Dover Publications, Нью-Йорк, штат Нью-Йорк (перепечатка издания Cambridge University Press 1918 года)