Мировая линия

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Материалы без источников могут быть оспорены и удалены. Найти источники:  «World line» – новости  · газеты  · книги  · ученый  · JSTOR ( ноябрь 2023 г. ) ( Узнайте, как и когда удалять это сообщение )

Общая теория относительности
${\displaystyle G_{\mu \nu }+\Lambda g_ {\mu \nu } = {\kappa }T_ {\mu \nu }}$
Введение История Хронология Тесты Математическая формулировка
Фундаментальные концепции Принцип эквивалентности Специальная теория относительности Мировая линия Псевдориманово многообразие
Феномены проблема Кеплера Гравитационное линзирование Гравитационное красное смещение Гравитационное замедление времени Гравитационные волны Перетаскивание кадров Геодезический эффект Горизонт событий Сингулярность Черная дыра Пространство-время Диаграммы пространства-времени пространство-время Минковского Мост Эйнштейна-Розена
Уравнения Формализмы Уравнения Линеаризованная гравитация Уравнения поля Эйнштейна Фридман Геодезические Матиссон–Папапетру–Диксон Гамильтон–Якоби–Эйнштейн Формализмы АДМ БССН Пост-ньютоновский Продвинутая теория Теория Калуцы–Клейна Квантовая гравитация
Решения Шварцшильд ( внутри ) Рейсснер–Нордстрём Волны Эйнштейна–Розена Червоточина Гёдель Керр Керр–Ньюман Керр–Ньюман–де Ситтер Каснер Леметр–Толман Тауб–НУТ Милн Робертсон–Уокер Оппенгеймер–Снайдер pp-волна пыль ван Штокума Вейль-Льюис-Папапетру Хартл–Торн
Ученые Эйнштейн Лоренц Гильберт Пуанкаре Шварцшильд де Ситтер Рейсснер Нордстрём Вейль Эддингтон Фридман Милн Цвикки Лемэтр Оппенгеймер Гёдель Уиллер Робертсон Бардин Уокер Керр Чандрасекар Элерс Пенроуз Хокинг Raychaudhuri Taylor Hulse van Stockum Taub Newman Yau Thorne others
Physics portal  Category
v t e

Мировая линия (или мировая линия ) объекта — это путь , который объект прокладывает в 4- мерном пространстве-времени . Это важное понятие современной физики , и в частности теоретической физики .

Понятие «мировая линия» отличается от таких понятий, как « орбита » или « траектория » (например, орбита планеты в космосе или траектория автомобиля на дороге) включением измерения времени и, как правило, охватывает большую область пространства-времени, в которой пути, которые воспринимаются как прямые, отображаются в виде кривых в пространстве-времени, чтобы показать их ( относительно ) более абсолютные состояния положения — чтобы раскрыть природу специальной теории относительности или гравитационных взаимодействий.

Идея мировых линий была выдвинута физиками и впервые предложена Германом Минковским . В настоящее время этот термин чаще всего используется в контексте теорий относительности (т. е. специальной теории относительности и общей теории относительности ).

Мировая линия объекта (обычно аппроксимируемая точкой в ​​пространстве, например, частицей или наблюдателем) — это последовательность событий пространства-времени, соответствующих истории объекта. Мировая линия — это особый тип кривой в пространстве-времени. Ниже будет объяснено эквивалентное определение: Мировая линия — это либо времениподобная, либо нулевая кривая в пространстве-времени. Каждая точка мировой линии — это событие, которое может быть помечено временем и пространственным положением объекта в это время.

Например, орбита Земли в космосе представляет собой приблизительно окружность, трехмерную (замкнутую) кривую в пространстве: Земля возвращается каждый год в одну и ту же точку пространства относительно Солнца. Однако она прибывает туда в разное (более позднее) время. Мировая линия Земли, таким образом, является винтовой в пространстве-времени (кривая в четырехмерном пространстве) и не возвращается в ту же точку.

Пространство-время — это совокупность событий вместе с непрерывной и гладкой системой координат , идентифицирующей события. Каждое событие можно обозначить четырьмя числами: временной координатой и тремя пространственными координатами; таким образом, пространство-время — это четырехмерное пространство. Математический термин для пространства-времени — четырехмерное многообразие (топологическое пространство, которое локально напоминает евклидово пространство вблизи каждой точки). Эта концепция может быть применена также к многомерному пространству. Для легкой визуализации четырех измерений две пространственные координаты часто опускаются. Затем событие представляется точкой на диаграмме Минковского , которая представляет собой плоскость, обычно построенную с временной координатой, скажем , по вертикали, и пространственной координатой, скажем , по горизонтали. Как выразился FR Harvey${\displaystyle t}$${\displaystyle x}$

Кривая M в [пространстве-времени] называется мировой линией частицы , если ее касательная подобна будущему времени в каждой точке. Параметр длины дуги называется собственным временем и обычно обозначается τ. Длина M называется собственным временем частицы. Если мировая линия M является отрезком прямой, то говорят, что частица находится в свободном падении . ^{[1] : 62–63}

Мировая линия вычерчивает путь одной точки в пространстве-времени. Мировой лист — это аналогичная двумерная поверхность, вычерченная одномерной линией (например, струной), проходящей через пространство-время. Мировой лист открытой струны (со свободными концами) — это полоска; мировой лист замкнутой струны (петли) напоминает трубку.

Если объект не аппроксимируется как простая точка, а имеет протяженный объем, то он описывает не мировую линию , а мировую трубку.

Одномерная линия или кривая может быть представлена ​​координатами как функция одного параметра. Каждое значение параметра соответствует точке в пространстве-времени, а изменение параметра вычерчивает линию. Таким образом, в математических терминах кривая определяется четырьмя функциями координат (где обычно обозначает временную координату), зависящими от одного параметра . Координатная сетка в пространстве-времени — это набор кривых, которые получаются, если три из четырех функций координат установить в константу.${\displaystyle x^{a}(\tau ),\;a=0,1,2,3}$${\displaystyle x^{0}}$${\displaystyle \tau }$

Иногда термин мировая линия неформально используется для любой кривой в пространстве-времени. Эта терминология вызывает путаницу. Более правильно, мировая линия — это кривая в пространстве-времени, которая отслеживает (временную) историю частицы, наблюдателя или малого объекта. Обычно в качестве параметра кривой вдоль мировой линии используется собственное время объекта или наблюдателя .${\displaystyle \tau }$

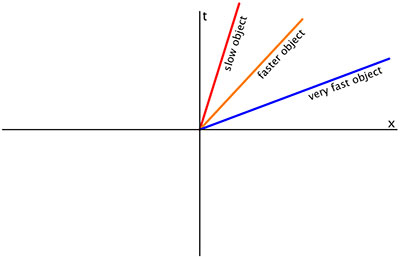
Кривая, состоящая из горизонтального отрезка (линии с постоянным координатным временем), может представлять стержень в пространстве-времени и не будет мировой линией в собственном смысле. Параметр просто отслеживает длину стержня.

Линия с постоянной пространственной координатой (вертикальная линия, согласно принятому выше соглашению) может представлять частицу в состоянии покоя (или неподвижного наблюдателя). Наклонная линия представляет частицу с постоянной координатной скоростью (постоянное изменение пространственной координаты с увеличением временной координаты). Чем больше линия наклонена от вертикали, тем больше скорость.

Две мировые линии, которые начинаются отдельно, а затем пересекаются, означают столкновение или «встречу». Две мировые линии, начинающиеся в одном и том же событии в пространстве-времени, каждая из которых следует своим собственным путем, могут представлять, например, распад частицы на две другие или испускание одной частицы другой.

Мировые линии частицы и наблюдателя могут быть взаимосвязаны с мировой линией фотона (путью света) и образовывать диаграмму, изображающую испускание фотона частицей, который впоследствии наблюдается наблюдателем (или поглощается другой частицей).

Четыре функции координат, определяющие мировую линию, являются функциями действительных чисел действительной переменной и могут быть просто дифференцированы с помощью обычного исчисления. Без существования метрики (это важно понимать) можно представить себе разницу между точкой на кривой при значении параметра и точкой на кривой немного (параметр ) дальше. В пределе эта разница, деленная на , определяет вектор, касательный вектор мировой линии в точке . Это четырехмерный вектор, определенный в точке . Он связан с нормальной 3-мерной скоростью объекта (но это не то же самое) и поэтому называется четырехскоростным , или в компонентах:${\displaystyle x^{a}(\tau ),\;a=0,1,2,3}$${\displaystyle \tau }$${\displaystyle p}$${\displaystyle \tau _{0}}$${\displaystyle \tau _{0}+\Delta \tau }$${\displaystyle \Delta \tau \to 0}$${\displaystyle \Delta \tau }$${\displaystyle p}$${\displaystyle p}$ ${\displaystyle {\vec {v}}}$$${\displaystyle {\vec {v}}=\left(v^{0},v^{1},v^{2},v^{3}\right)=\left({\frac {dx^{0}}{d\tau }}\;,{\frac {dx^{1}}{d\tau }}\;,{\frac {dx^{2}}{d\tau }}\;,{\frac {dx^{3}}{d\tau }}\right)}$$

таким образом, что производные берутся в точке , поэтому при .${\displaystyle p}$${\displaystyle \tau =\tau _{0}}$

Все кривые, проходящие через точку p, имеют касательный вектор, а не только мировые линии. Сумма двух векторов снова является касательным вектором к некоторой другой кривой, и то же самое справедливо для умножения на скаляр. Таким образом, все касательные векторы для точки p охватывают линейное пространство , называемое касательным пространством в точке p. Например, если взять двумерное пространство, такое как (искривленная) поверхность Земли, то ее касательное пространство в определенной точке будет плоским приближением искривленного пространства.

До сих пор мировая линия (и концепция касательных векторов) описывалась без средств количественной оценки интервала между событиями. Основная математика такова: Теория специальной теории относительности накладывает некоторые ограничения на возможные мировые линии. В специальной теории относительности описание пространства-времени ограничивается специальными системами координат, которые не ускоряются (и, следовательно, не вращаются), называемыми инерциальными системами координат . В таких системах координат скорость света является константой. Структура пространства-времени определяется билинейной формой η, которая дает действительное число для каждой пары событий. Билинейная форма иногда называется метрикой пространства-времени , но поскольку отдельные события иногда приводят к нулевому значению, в отличие от метрик в метрических пространствах математики, билинейная форма не является математической метрикой пространства-времени.

Мировые линии свободно падающих частиц/объектов называются геодезическими . В специальной теории относительности это прямые линии в пространстве Минковского .

Часто единицы времени выбираются таким образом, что скорость света представляется линиями под фиксированным углом, обычно в 45 градусов, образуя конус с вертикальной (временной) осью. В общем, полезные кривые в пространстве-времени могут быть трех типов (другие типы будут частично одного, частично другого типа):

• Светоподобные кривые, имеющие в каждой точке скорость света. Они образуют конус в пространстве-времени, разделяя его на две части. Конус трехмерен в пространстве-времени, выглядит как линия на рисунках с подавленными двумя измерениями и как конус на рисунках с подавленным одним пространственным измерением.

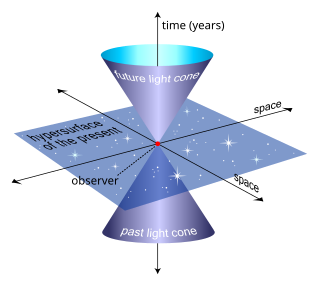
• времениподобные кривые, со скоростью, меньшей скорости света. Эти кривые должны попадать в конус, определяемый светоподобными кривыми. В нашем определении выше: мировые линии являются времениподобными кривыми в пространстве-времени .
• пространственно-подобные кривые, падающие за пределы светового конуса. Такие кривые могут описывать, например, длину физического объекта. Окружность цилиндра и длина стержня являются пространственно-подобными кривыми.

При заданном событии на мировой линии пространство-время ( пространство Минковского ) делится на три части.

• Будущее данного события формируется всеми событиями, которые могут быть достигнуты посредством времениподобных кривых, лежащих внутри будущего светового конуса.
• Прошлое данного события формируется всеми событиями, которые могут повлиять на событие (то есть которые могут быть связаны мировыми линиями внутри светового конуса прошлого с данным событием).
  • Световой конус в данном событии формируется всеми событиями, которые могут быть связаны с событием посредством световых лучей. Когда мы наблюдаем небо ночью, мы в основном видим только прошлый световой конус в пределах всего пространства-времени.
• Elsewhere — это область между двумя световыми конусами. Точки в where of наблюдателя недоступны для них; только точки в прошлом могут посылать сигналы наблюдателю. В обычном лабораторном опыте, используя общие единицы и методы измерения, может показаться, что мы смотрим на настоящее, но на самом деле всегда есть задержка времени для распространения света. Например, мы видим Солнце таким , каким оно было около 8 минут назад, а не таким, какое оно «прямо сейчас». В отличие от настоящего в галилеевской/ньютоновской теории, where of является толстым; это не 3-мерный объем, а 4-мерная область пространства-времени.
  • В "elsewhere" включена одновременная гиперплоскость , которая определяется для данного наблюдателя пространством , которое гиперболически-ортогонально его мировой линии. Она действительно трехмерна, хотя на диаграмме это была бы 2-плоскость, потому что нам пришлось отбросить одно измерение, чтобы сделать понятную картину. Хотя световые конусы одинаковы для всех наблюдателей в данном событии пространства-времени, разные наблюдатели, с разными скоростями, но совпадающие в событии (точке) в пространстве-времени, имеют мировые линии, пересекающиеся друг с другом под углом, определяемым их относительными скоростями, и, таким образом, они имеют разные одновременные гиперплоскости.
  • Под настоящим часто подразумевается отдельное рассматриваемое пространственно-временное событие.

Поскольку мировая линия определяет 4-вектор скорости , который является времениподобным, форма Минковского определяет линейную функцию Пусть N будет нулевым пространством этого линейного функционала. Тогда N называется одновременной гиперплоскостью относительно v . Относительность одновременности - это утверждение, что N зависит от v . Действительно, N является ортогональным дополнением v относительно η. Когда две мировые линии u и w связаны, то они разделяют одну и ту же одновременную гиперплоскость. Эта гиперплоскость существует математически, но физические отношения в теории относительности включают перемещение информации посредством света. Например, традиционная электростатическая сила, описываемая законом Кулона, может быть изображена в одновременной гиперплоскости, но релятивистские отношения заряда и силы включают запаздывающие потенциалы .${\displaystyle w(\tau )\in R^{4}}$${\displaystyle v={\frac {dw}{d\tau }}}$${\displaystyle \eta (v,x)}$${\displaystyle R^{4}\rightarrow R}$${\displaystyle x\mapsto \eta (v,x).}$${\displaystyle {\frac {du}{d\tau }}={\frac {dw}{d\tau }},}$

Использование мировых линий в общей теории относительности в основном такое же, как и в специальной теории относительности , с той разницей, что пространство-время может быть искривлено . Метрика существует, и ее динамика определяется уравнениями поля Эйнштейна и зависит от распределения массы-энергии в пространстве-времени. Опять же, метрика определяет светоподобные (нулевые), пространственноподобные и времениподобные кривые. Кроме того, в общей теории относительности мировые линии включают времениподобные кривые и нулевые кривые в пространстве-времени, где времениподобные кривые попадают в световой конус. Однако световой конус не обязательно наклонен под углом 45 градусов к оси времени. Однако это артефакт выбранной системы координат и отражает свободу координат ( инвариантность диффеоморфизма ) общей теории относительности. Любая времениподобная кривая допускает сопутствующего наблюдателя, «ось времени» которого соответствует этой кривой, и, поскольку ни один наблюдатель не является привилегированным, мы всегда можем найти локальную систему координат, в которой световые конусы наклонены под углом 45 градусов к оси времени. См. также, например, координаты Эддингтона-Финкельштейна .

Мировые линии свободно падающих частиц или объектов (например, планет вокруг Солнца или астронавта в космосе) называются геодезическими .

Квантовая теория поля, структура, в которой описывается вся современная физика элементарных частиц, обычно описывается как теория квантованных полей. Однако, хотя это и не получило широкого признания, со времен Фейнмана ^[2] было известно , что многие квантовые теории поля могут быть эквивалентно описаны в терминах мировых линий. Это предшествовало многим его работам ^[3] по формулировке, которая позже стала более стандартной. Формулировка мировой линии квантовой теории поля оказалась особенно плодотворной для различных вычислений в калибровочных теориях ^{[4] [5] [6]} и при описании нелинейных эффектов электромагнитных полей. ^{[7] [8]}

В 1884 году CH Hinton написал эссе «Что такое четвертое измерение?», которое он опубликовал в виде научного романа . Он написал

Почему же тогда четырехмерными существами не должны быть мы сами, а наши последовательные состояния – их прохождение через трехмерное пространство, которым ограничено наше сознание. ^{[9] : 18–19}

Популярное описание человеческих мировых линий было дано Дж. К. Филдсом в Университете Торонто в ранние дни теории относительности. Как описал юрист из Торонто Норман Робертсон:

Я помню, как [Филдс] читал лекцию на одной из субботних вечерних лекций в Королевском канадском институте . Это было объявлено как «Математическая фантазия» — и так оно и было! Суть упражнения была следующей: он постулировал, что, начиная с его рождения, каждое человеческое существо имеет некую духовную ауру с длинной прикрепленной нитью или нитью, которая путешествовала позади него на протяжении всей его жизни. Затем он продолжил в воображении описывать сложную запутанность, в которую каждый человек был вовлечен в своих отношениях с другими людьми, сравнивая простые запутанности юности с теми сложными узлами, которые развиваются в более поздней жизни. ^[10]

Курт Воннегут в своем романе «Бойня номер пять » описывает мировые линии звезд и людей:

«Билли Пилигрим говорит, что Вселенная не выглядит как множество ярких маленьких точек для существ с Тральфамадора. Существа могут видеть, где была каждая звезда и куда она движется, так что небеса заполнены разреженными, светящимися спагетти. И тральфамадорцы также не видят людей как двуногих существ. Они видят их как огромных тысяченог — «с ножками младенцев на одном конце и ногами стариков на другом», — говорит Билли Пилигрим».

Почти все научно-фантастические рассказы, которые активно используют эту концепцию, например, для того, чтобы сделать возможным путешествие во времени , чрезмерно упрощают эту концепцию до одномерной временной шкалы, чтобы соответствовать линейной структуре, которая не соответствует моделям реальности. Такие машины времени часто изображаются как мгновенные, с ее содержимым, отправляющимся в одно время и прибывающим в другое, но в одну и ту же буквальную географическую точку в пространстве. Это часто выполняется без указания системы отсчета или с неявным предположением, что система отсчета локальна; как таковое, это потребовало бы либо точной телепортации, поскольку вращающаяся планета, находящаяся под ускорением, не является инерциальной системой, либо для машины времени, чтобы оставаться в том же месте, ее содержимое «заморожено».

Автор Оливер Франклин опубликовал в 2008 году научно-фантастическое произведение под названием «Мировые линии» , в котором он дал упрощенное объяснение гипотезы для неспециалистов. ^[11]

В рассказе «Линия жизни» автор Роберт А. Хайнлайн описывает мировую линию человека: ^[12]

Он подошел к одному из репортеров. «Предположим, мы возьмем вас в качестве примера. Вас зовут Роджерс, не так ли? Очень хорошо, Роджерс, вы — пространственно-временное событие, имеющее длительность в четырех направлениях. Вы не совсем шести футов ростом, вы около двадцати дюймов в ширину и, возможно, десять дюймов в толщину. Со временем за вами простирается больше этого пространственно-временного события, достигая, возможно, девятнадцатого года, поперечное сечение которого мы видим здесь под прямым углом к ​​оси времени, и такое же толстое, как настоящее. На дальнем конце — младенец, пахнущий кислым молоком и пускающий слюни от завтрака на свой нагрудник. На другом конце, возможно, лежит старик где-то в восьмидесятых годах.

«Представьте себе это пространственно-временное событие, которое мы называем Роджерсом, как длинного розового червя, продолжающегося на протяжении многих лет, один конец которого находится в утробе матери, а другой — у могилы...»

Этот термин используется в романе Хайнлайна « Дети Мафусаила» ​​и в романе Джеймса Блиша «Квинканс времени» (расширенное название «Пипа»).

Визуальный роман под названием Steins;Gate , созданный 5pb. , рассказывает историю, основанную на смещении мировых линий. Steins;Gate является частью серии " Science Adventure ". Мировые линии и другие физические концепции, такие как море Дирака, также используются на протяжении всей серии.

Роман Нила Стивенсона « Анафем» включает в себя долгое обсуждение мировых линий за ужином в разгар философского спора между платоновским реализмом и номинализмом .

«Абсолютный выбор» изображает различные мировые линии как подсюжет и сеттинговый прием.

Космическая армада, пытающаяся пройти по (почти) замкнутому временному пути в качестве стратегического маневра, образует фон и основной сюжетный ход романа «Небо сингулярности» Чарльза Стросса .

• Конкретные типы мировых линий
  • Геодезические
  • Замкнутые времениподобные кривые
  • Причинно-следственная структура , кривые, представляющие собой различные типы мировых линий.
  • Изотропная линия
• Диаграмма Фейнмана
• География времени

• Минковский, Герман (1909), «Raum und Zeit»  , Physikalische Zeitschrift , 10 : 75–88.

• Различные переводы на английский язык на Wikisource: Space and Time

• Людвик Зильберштейн (1914) Теория относительности , стр. 130, Macmillan and Company .

• Статья о мировых линиях на h2g2 .

• подробный текст о мировых линиях и специальной теории относительности