Вектор пространства
В математике и физике векторное пространство (также называемое линейным пространством ) — это множество , элементы которого, часто называемые векторами , можно складывать и умножать («масштабировать») на числа, называемые скалярами . Операции сложения векторов и умножения скаляров должны удовлетворять определенным требованиям, называемым аксиомами вектора . Действительные векторные пространства и комплексные векторные пространства — это виды векторных пространств, основанные на различных видах скаляров: действительных числах и комплексных числах . Скаляры также могут быть, в более общем смысле, элементами любого поля .
Векторные пространства обобщают евклидовы векторы , которые позволяют моделировать физические величины (такие как силы и скорости ), которые имеют не только величину , но и направление . Концепция векторных пространств является фундаментальной для линейной алгебры , вместе с концепцией матриц , которая позволяет производить вычисления в векторных пространствах. Это обеспечивает краткий и синтетический способ манипулирования и изучения систем линейных уравнений .
Векторные пространства характеризуются своей размерностью , которая, грубо говоря, определяет число независимых направлений в пространстве. Это означает, что для двух векторных пространств над заданным полем и с одинаковой размерностью свойства, зависящие только от структуры векторного пространства, в точности одинаковы (технически векторные пространства изоморфны ) . Векторные пространства являются конечномерными, если их размерность является натуральным числом . В противном случае они являются бесконечномерными , а их размерность является бесконечным кардиналом . Конечномерные векторные пространства естественным образом встречаются в геометрии и смежных областях. Бесконечномерные векторные пространства встречаются во многих областях математики. Например, полиномиальные кольца являются счетно -бесконечномерными векторными пространствами, а многие функциональные пространства имеют мощность континуума в качестве размерности.
Многие векторные пространства, рассматриваемые в математике, также наделены другими структурами . Это случай алгебр , которые включают расширения полей , кольца полиномов, ассоциативные алгебры и алгебры Ли . Это также случай топологических векторных пространств , которые включают функциональные пространства, пространства скалярного произведения , нормированные пространства , гильбертовы пространства и банаховы пространства .
| Алгебраические структуры |
|---|
Определение и основные свойства
В этой статье векторы выделены жирным шрифтом, чтобы отличать их от скаляров. [nb 1] [1]
Векторным пространством над полем F называется непустое множество V вместе с бинарной операцией и бинарной функцией , которые удовлетворяют восьми аксиомам, перечисленным ниже. В этом контексте элементы V обычно называются векторами , а элементы F называются скалярами . [2]
- Бинарная операция, называемая сложением векторов или просто сложением, присваивает любым двум векторам v и w из V третий вектор из V , который обычно записывается как v + w и называется суммой этих двух векторов.
- Бинарная функция, называемая скалярным умножением , присваивает любому скаляру a в F и любому вектору v в V другой вектор в V , который обозначается a v . [nb 2]
Чтобы иметь векторное пространство, должны быть выполнены восемь следующих аксиом для каждых u , v и w в V , а также a и b в F. [3 ]
| Аксиома | Заявление |
|---|---|
| Ассоциативность векторного сложения | и + ( в + ш ) = ( и + в ) + ш |
| Коммутативность сложения векторов | у + в = в + у |
| Элемент тождественности векторного сложения | Существует элемент 0 ∈ V , называемый нулевым вектором , такой, что v + 0 = v для всех v ∈ V . |
| Обратные элементы векторного сложения | Для каждого v ∈ V существует элемент − v ∈ V , называемый аддитивным обратным к v , такой, что v + (− v ) = 0 . |
| Совместимость скалярного умножения с полевым умножением | а ( б в ) = ( аб ) в [число 3] |
| Элемент тождественности скалярного умножения | 1 v = v , где 1 обозначает мультипликативное тождество в F . |
| Распределимость скалярного умножения относительно векторного сложения | а ( и + v ) = а у + а v |
| Распределимость скалярного умножения относительно сложения полей | ( а + б ) в = а в + б в |
Когда скалярное поле — это действительные числа , векторное пространство называется действительным векторным пространством , а когда скалярное поле — это комплексные числа , векторное пространство называется комплексным векторным пространством . [4] Эти два случая являются наиболее распространенными, но также обычно рассматриваются векторные пространства со скалярами в произвольном поле F. Такое векторное пространство называется F - векторным пространством или векторным пространством над F. [5 ]
Можно дать эквивалентное определение векторного пространства, которое гораздо более кратко, но менее элементарно: первые четыре аксиомы (относящиеся к сложению векторов) говорят, что векторное пространство является абелевой группой относительно сложения, а четыре оставшиеся аксиомы (относящиеся к скалярному умножению) говорят, что эта операция определяет кольцевой гомоморфизм из поля F в кольцо эндоморфизмов этой группы. [6]
Вычитание двух векторов можно определить как
Прямые следствия аксиом включают то, что для каждого и одного есть
- подразумевает или
Еще более кратко, векторное пространство — это модуль над полем . [ 7]
Базы, векторные координаты и подпространства

- Линейная комбинация
- Для заданного множества G элементов F -векторного пространства V линейная комбинация элементов G — это элемент V вида где и Скаляры называются коэффициентами линейной комбинации. [8]
- Линейная независимость
- Элементы подмножества G F - векторного пространства V называются линейно независимыми , если ни один элемент G не может быть записан в виде линейной комбинации других элементов G. Эквивалентно, они линейно независимы, если две линейные комбинации элементов G определяют один и тот же элемент V тогда и только тогда, когда они имеют одинаковые коэффициенты. Также эквивалентно, они линейно независимы, если линейная комбинация приводит к нулевому вектору тогда и только тогда, когда все ее коэффициенты равны нулю. [9]
- Линейное подпространство
- Линейное подпространство или векторное подпространство W векторного пространства V — это непустое подмножество V , замкнутое относительно сложения векторов и скалярного умножения; то есть сумма двух элементов W и произведение элемента W на скаляр принадлежат W . [10] Это означает, что каждая линейная комбинация элементов W принадлежит W . Линейное подпространство — это векторное пространство для индуцированного сложения и скалярного умножения; это означает, что свойство замкнутости подразумевает, что аксиомы векторного пространства выполнены. [11]
Свойство замкнутости также подразумевает, что каждое пересечение линейных подпространств является линейным подпространством. [11] - Линейный промежуток
- Если задано подмножество G векторного пространства V , линейная оболочка или просто оболочка G является наименьшим линейным подпространством V , которое содержит G , в том смысле, что это пересечение всех линейных подпространств, которые содержат G . Охват G также является множеством всех линейных комбинаций элементов G . Если W является охватом G , говорят, что G охватывает или порождает W , и что G является охватывающим множеством или порождающим множеством W . [ 12]
- Основа и размерность
- Подмножество векторного пространства является базисом , если его элементы линейно независимы и охватывают векторное пространство. [13] Каждое векторное пространство имеет по крайней мере один базис, или, в общем случае, несколько (см. Базис (линейная алгебра) § Доказательство того, что каждое векторное пространство имеет базис ). [14] Более того, все базисы векторного пространства имеют одинаковую мощность , которая называется размерностью векторного пространства (см. Теорема о размерности для векторных пространств ). [15] Это фундаментальное свойство векторных пространств, которое подробно рассматривается в оставшейся части раздела.
Базисы являются фундаментальным инструментом для изучения векторных пространств, особенно когда размерность конечна. В бесконечномерном случае существование бесконечных базисов, часто называемых базисами Гамеля , зависит от аксиомы выбора . Из этого следует, что в общем случае ни один базис не может быть явно описан. [16] Например, действительные числа образуют бесконечномерное векторное пространство над рациональными числами , для которого неизвестен конкретный базис.
Рассмотрим базис векторного пространства V размерности n над полем F . Определение базиса подразумевает, что каждый может быть записан с помощью в F , и что это разложение является единственным. Скаляры называются координатами v на базисе. Они также называются коэффициентами разложения v на базисе. Также говорят, что n -кортеж координат является координатным вектором v на базисе, поскольку множество n -кортежей элементов F является векторным пространством для покомпонентного сложения и скалярного умножения, размерность которого равна n .
Соответствие один к одному между векторами и их координатными векторами отображает векторное сложение в векторное сложение и скалярное умножение в скалярное умножение. Таким образом, это изоморфизм векторного пространства , который позволяет переводить рассуждения и вычисления над векторами в рассуждения и вычисления над их координатами. [17]
История
Векторные пространства происходят из аффинной геометрии , через введение координат на плоскости или трехмерном пространстве. Около 1636 года французские математики Рене Декарт и Пьер де Ферма основали аналитическую геометрию , определив решения уравнения двух переменных с точками на плоской кривой . [18] Чтобы получить геометрические решения без использования координат, Больцано ввел в 1804 году определенные операции над точками, прямыми и плоскостями, которые являются предшественниками векторов. [19] Мёбиус (1827) ввел понятие барицентрических координат . [20] Беллавитис (1833) ввел отношение эквивалентности на направленных отрезках прямых, которые имеют одинаковую длину и направление, которое он назвал равносильностью . [21] Тогда евклидов вектор является классом эквивалентности этого отношения. [22]
Векторы были пересмотрены с представлением комплексных чисел Арганом и Гамильтоном и введением последним кватернионов . [23] Они являются элементами в R2 и R4 ; их рассмотрение с использованием линейных комбинаций восходит к Лагерру в 1867 году, который также определил системы линейных уравнений .
В 1857 году Кэли ввел матричную нотацию , которая позволяет гармонизировать и упростить линейные отображения . Примерно в то же время Грассман изучал барицентрическое исчисление, начатое Мёбиусом. Он рассматривал множества абстрактных объектов, наделенных операциями. [24] В его работе присутствуют концепции линейной независимости и размерности , а также скалярных произведений . Работа Грассмана 1844 года также выходит за рамки векторных пространств, поскольку его рассмотрение умножения привело его к тому, что сегодня называется алгебрами . Итальянский математик Пеано был первым, кто дал современное определение векторных пространств и линейных отображений в 1888 году, [25] хотя он называл их «линейными системами». [26] Аксиоматизация Пеано допускала векторные пространства с бесконечной размерностью, но Пеано не развивал эту теорию дальше. В 1897 году Сальваторе Пинкерле принял аксиомы Пеано и сделал первые шаги в теории бесконечномерных векторных пространств. [27]
Важное развитие векторных пространств связано с построением функциональных пространств Анри Лебегом . Позднее это было формализовано Банахом и Гильбертом около 1920 года. [28] В то время алгебра и новая область функционального анализа начали взаимодействовать, в частности, с такими ключевыми концепциями, как пространства p -интегрируемых функций и пространства Гильберта . [29]
Примеры
Стрелки в плоскости
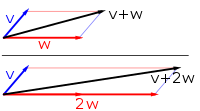
Первый пример векторного пространства состоит из стрелок в фиксированной плоскости , начинающихся в одной фиксированной точке. Это используется в физике для описания сил или скоростей . [30] Если заданы любые две такие стрелки, v и w , параллелограмм, натянутый на эти две стрелки, содержит одну диагональную стрелку, которая также начинается в начале координат. Эта новая стрелка называется суммой двух стрелок и обозначается v + w . В особом случае двух стрелок на одной прямой их сумма — это стрелка на этой прямой, длина которой равна сумме или разности длин, в зависимости от того, имеют ли стрелки одинаковое направление. Другая операция, которую можно выполнить со стрелками, — это масштабирование: если задано любое положительное действительное число a , стрелка, имеющая то же направление, что и v , но расширяющаяся или сжимающаяся путем умножения ее длины на a , называется умножением v на a . Она обозначается a v . Когда a отрицательно, a v определяется как стрелка, указывающая в противоположном направлении. [ 31]
Ниже приведены несколько примеров: если a = 2 , то результирующий вектор a w имеет то же направление, что и w , но растянут до двойной длины w (второе изображение). Эквивалентно, 2 w является суммой w + w . Более того, (−1) v = − v имеет противоположное направление и ту же длину, что и v (синий вектор, направленный вниз на втором изображении).
Упорядоченные пары чисел
Второй ключевой пример векторного пространства предоставляется парами действительных чисел x и y . Порядок компонентов x и y имеет значение, поэтому такая пара также называется упорядоченной парой . Такая пара записывается как ( x , y ) . Сумма двух таких пар и умножение пары на число определяется следующим образом: [32]
Первый пример выше сводится к этому примеру, если стрелка представлена парой декартовых координат ее конечной точки.
Координатное пространство
Простейшим примером векторного пространства над полем F является само поле F с его сложением, рассматриваемым как векторное сложение, и его умножением, рассматриваемым как скалярное умножение. В более общем смысле, все n -кортежи (последовательности длины n ) элементов a i поля F образуют векторное пространство, которое обычно обозначается F n и называется координатным пространством . [33] Случай n = 1 является вышеупомянутым простейшим примером, в котором поле F также рассматривается как векторное пространство над собой. Случай F = R и n = 2 (то есть R 2 ) сводится к предыдущему примеру.
Комплексные числа и другие расширения полей
Множество комплексных чисел C , чисел, которые можно записать в виде x + iy для действительных чисел x и y , где i — мнимая единица , образуют векторное пространство над действительными числами с обычным сложением и умножением: ( x + iy ) + ( a + ib ) = ( x + a ) + i ( y + b ) и c ⋅ ( x + iy ) = ( c ⋅ x ) + i ( c ⋅ y ) для действительных чисел x , y , a , b и c . Различные аксиомы векторного пространства вытекают из того факта, что те же правила справедливы для арифметики комплексных чисел. Пример комплексных чисел по сути тот же самый (то есть он изоморфен ) векторному пространству упорядоченных пар действительных чисел, упомянутому выше: если мы думаем о комплексном числе x + i y как о представлении упорядоченной пары ( x , y ) в комплексной плоскости , то мы видим, что правила сложения и скалярного умножения точно соответствуют тем, что были в предыдущем примере.
В более общем смысле расширения полей представляют собой другой класс примеров векторных пространств, особенно в алгебре и алгебраической теории чисел : поле F, содержащее меньшее поле E, является E -векторным пространством, с помощью заданных операций умножения и сложения F. [34] Например, комплексные числа являются векторным пространством над R , а расширение поля является векторным пространством над Q.
Функциональные пространства

Функции из любого фиксированного множества Ω в поле F также образуют векторные пространства, выполняя сложение и скалярное умножение поточечно. То есть, сумма двух функций f и g является функцией, заданной и аналогично для умножения. Такие функциональные пространства встречаются во многих геометрических ситуациях, когда Ω является действительной линией или интервалом , или другими подмножествами R. Многие понятия в топологии и анализе, такие как непрерывность , интегрируемость или дифференцируемость, хорошо ведут себя по отношению к линейности: суммы и скалярные кратные функций, обладающие таким свойством, по-прежнему обладают этим свойством. [35] Следовательно, множество таких функций являются векторными пространствами, изучение которых относится к функциональному анализу .
Линейные уравнения
Системы однородных линейных уравнений тесно связаны с векторными пространствами. [36] Например, решения задаются тройками с произвольными и Они образуют векторное пространство: суммы и скалярные кратные таких троек по-прежнему удовлетворяют тем же соотношениям трех переменных; таким образом, они также являются решениями. Матрицы могут использоваться для конденсации нескольких линейных уравнений, как указано выше, в одно векторное уравнение, а именно
где — матрица, содержащая коэффициенты данных уравнений, — вектор обозначает произведение матриц , а — нулевой вектор. Аналогичным образом, решения однородных линейных дифференциальных уравнений образуют векторные пространства. Например,
дает где и — произвольные константы, а — естественная экспоненциальная функция .
Линейные карты и матрицы
Связь двух векторных пространств может быть выражена линейным отображением или линейным преобразованием . Это функции , которые отражают структуру векторного пространства, то есть сохраняют суммы и скалярное умножение: для всех и во всех в [37]
Изоморфизм — это линейное отображение f : V → W такое , что существует обратное отображение g : W → V , которое является отображением таким, что две возможные композиции f ∘ g : W → W и g ∘ f : V → V являются тождественными отображениями . Эквивалентно, f является как взаимно-однозначным ( инъективным ), так и на ( сюръективным ). [38] Если существует изоморфизм между V и W , то два пространства называются изоморфными ; тогда они по существу идентичны как векторные пространства, поскольку все тождества, имеющие место в V , посредством f переносятся в подобные тождества в W , и наоборот посредством g .
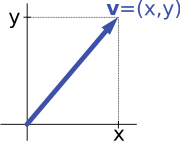
Например, стрелки на плоскости и упорядоченные пары чисел векторных пространств во введении выше (см. § Примеры) изоморфны: плоская стрелка v, выходящая из начала некоторой (фиксированной) системы координат, может быть выражена как упорядоченная пара, если рассмотреть x - и y -компоненты стрелки, как показано на изображении справа. Наоборот, если задана пара ( x , y ) , стрелка, идущая по x вправо (или влево, если x отрицателен), и по y вверх (вниз, если y отрицателен), возвращает стрелку v . [39]
Линейные отображения V → W между двумя векторными пространствами образуют векторное пространство Hom F ( V , W ) , также обозначаемое L( V , W ) или 𝓛( V , W ) . [40] Пространство линейных отображений из V в F называется дуальным векторным пространством и обозначается V ∗ . [41] С помощью инъективного естественного отображения V → V ∗∗ любое векторное пространство может быть вложено в его бидуальное ; отображение является изоморфизмом тогда и только тогда, когда пространство конечномерно. [42]
После выбора базиса V линейные отображения f : V → W полностью определяются указанием образов базисных векторов, поскольку любой элемент V однозначно выражается как их линейная комбинация. [43] Если dim V = dim W , то взаимно однозначное соответствие между фиксированными базисами V и W приводит к линейному отображению, которое отображает любой базисный элемент V в соответствующий базисный элемент W . Это является изоморфизмом по самому своему определению. [44] Следовательно, два векторных пространства над заданным полем изоморфны, если их размерности совпадают, и наоборот. Другой способ выразить это состоит в том, что любое векторное пространство над заданным полем полностью классифицируется ( с точностью до изоморфизма) своей размерностью, одним числом. В частности, любое n -мерное F -векторное пространство V изоморфно F n . Однако не существует «канонического» или предпочтительного изоморфизма; изоморфизм φ : F n → V эквивалентен выбору базиса V путем отображения стандартного базиса F n в V посредством φ .
Матрицы

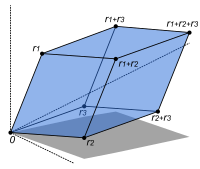
Матрицы являются полезным понятием для кодирования линейных отображений. [45] Они записываются как прямоугольный массив скаляров, как на изображении справа. Любая матрица m на n порождает линейное отображение из F n в F m , следующим образом , где обозначает суммирование , или с помощью матричное умножение матрицы на координатный вектор :
Более того, после выбора базисов V и W любое линейное отображение f : V → W однозначно представляется матрицей посредством этого назначения. [46]
Определитель det ( A ) квадратной матрицы A — это скаляр, который сообщает, является ли связанное отображение изоморфизмом или нет: для этого достаточно и необходимо, чтобы определитель был ненулевым. [47] Линейное преобразование R n , соответствующее действительной матрице размером n на n , сохраняет ориентацию тогда и только тогда, когда ее определитель положителен.
Собственные значения и собственные векторы
Эндоморфизмы , линейные отображения f : V → V , особенно важны, поскольку в этом случае векторы v можно сравнить с их образом при f , f ( v ) . Любой ненулевой вектор v , удовлетворяющий λ v = f ( v ) , где λ — скаляр, называется собственным вектором f с собственным значением λ . [48] Эквивалентно, v является элементом ядра разности f − λ · Id (где Id — тождественное отображение V → V ) . Если V конечномерно, это можно перефразировать с использованием определителей: f , имеющая собственное значение λ , эквивалентна Излагая определение определителя, можно увидеть, что выражение в левой части является полиномиальной функцией от λ , называемой характеристическим полиномом f . [49] Если поле F достаточно велико, чтобы содержать ноль этого многочлена (что автоматически происходит для F алгебраически замкнутого , такого как F = C ), любая линейная карта имеет по крайней мере один собственный вектор. Векторные пространства V могут иметь или не иметь собственный базис , базис, состоящий из собственных векторов. Это явление регулируется канонической формой Жордана карты. [50] Набор всех собственных векторов, соответствующих конкретному собственному значению f, образует векторное пространство, известное как собственное пространство, соответствующее рассматриваемому собственному значению (и f ).
Базовые конструкции
Помимо приведенных выше конкретных примеров, существует ряд стандартных линейных алгебраических конструкций, которые дают векторные пространства, связанные с заданными.
Подпространства и факторпространства

Непустое подмножество векторного пространства , замкнутое относительно сложения и скалярного умножения (и, следовательно, содержащее -вектор из ), называется линейным подпространством из , или просто подпространством из , когда окружающее пространство однозначно является векторным пространством. [51] [nb 4] Подпространства из являются векторными пространствами (над тем же полем) сами по себе. Пересечение всех подпространств , содержащих заданный набор векторов, называется его охватом , и это наименьшее подпространство из , содержащее набор . Выраженный в терминах элементов, охват является подпространством, состоящим из всех линейных комбинаций элементов из . [52]
Линейные подпространства размерности 1 и 2 называются линией ( также векторной линией ) и плоскостью соответственно. Если W является n -мерным векторным пространством, любое подпространство размерности на 1 меньше, т.е. размерности называется гиперплоскостью . [53]
Аналогом подпространств являются факторные векторные пространства . [54] Для любого подпространства факторное пространство (« по модулю ») определяется следующим образом: как множество, оно состоит из , где — произвольный вектор из . Сумма двух таких элементов и равна , а скалярное умножение задается выражением . Ключевым моментом в этом определении является то, что тогда и только тогда, когда разность и лежит в . [nb 5] Таким образом, факторное пространство «забывает» информацию, которая содержится в подпространстве .
Ядро линейного отображения состоит из векторов , которые отображаются в . [55] Ядро и изображение являются подпространствами и , соответственно. [56 ]
Важным примером является ядро линейного отображения для некоторой фиксированной матрицы . Ядро этого отображения представляет собой подпространство векторов, таких что , что в точности является множеством решений системы однородных линейных уравнений, принадлежащих . Это понятие распространяется также на линейные дифференциальные уравнения , где коэффициенты являются функциями в тоже. В соответствующем отображении производные функции появляются линейно (в отличие от , например). Поскольку дифференцирование является линейной процедурой (то есть и для константы ), это назначение является линейным, называемым линейным дифференциальным оператором . В частности, решения дифференциального уравнения образуют векторное пространство (над R или C ). [57]
Существование ядер и образов является частью утверждения о том, что категория векторных пространств (над фиксированным полем ) является абелевой категорией , то есть совокупностью математических объектов и сохраняющих структуру отображений между ними ( категорией ), которая ведет себя во многом подобно категории абелевых групп . [58] Благодаря этому многие утверждения, такие как первая теорема об изоморфизме (также называемая теоремой о ранге–ничтожности в терминах, связанных с матрицами) и вторая и третья теоремы об изоморфизме, могут быть сформулированы и доказаны способом, очень похожим на соответствующие утверждения для групп .
Прямое произведение и прямая сумма
Прямое произведение векторных пространств и прямая сумма векторных пространств — это два способа объединения индексированного семейства векторных пространств в новое векторное пространство.
Прямое произведение семейства векторных пространств состоит из множества всех кортежей , которые определяют для каждого индекса в некотором наборе индексов элемент из . [59] Сложение и скалярное умножение выполняются покомпонентно. Вариантом этой конструкции является прямая сумма (также называемая копроизведением и обозначаемая ), где разрешены только кортежи с конечным числом ненулевых векторов. Если набор индексов конечен, две конструкции согласуются, но в целом они различны.
Тензорное произведение
Тензорное произведение или просто двух векторных пространств и является одним из центральных понятий полилинейной алгебры , которая занимается расширением таких понятий, как линейные отображения для нескольких переменных. Отображение из декартового произведения называется билинейным, если линейно по обеим переменным и То есть, для фиксированного отображение линейно в указанном выше смысле и аналогично для фиксированного

Тензорное произведение — это конкретное векторное пространство, которое является универсальным получателем билинейных отображений следующим образом. Оно определяется как векторное пространство, состоящее из конечных (формальных) сумм символов, называемых тензорами, подчиняющихся правилам [60] Эти правила гарантируют, что отображение из в , отображающее кортеж в , является билинейным. Универсальность утверждает, что для любого векторного пространства и любого билинейного отображения существует уникальное отображение, показанное на диаграмме пунктирной стрелкой, композиция которого с равна [61] Это называется универсальным свойством тензорного произведения, примером метода — часто используемого в продвинутой абстрактной алгебре — для косвенного определения объектов путем указания отображений из или в этот объект.
Векторные пространства с дополнительной структурой
С точки зрения линейной алгебры векторные пространства полностью понятны, поскольку любое векторное пространство над заданным полем характеризуется, с точностью до изоморфизма, своей размерностью. Однако векторные пространства сами по себе не предлагают структуру для решения вопроса — решающего для анализа — сходится ли последовательность функций к другой функции. Аналогично, линейная алгебра не приспособлена для работы с бесконечными рядами , поскольку операция сложения позволяет добавлять только конечное число членов. Поэтому потребности функционального анализа требуют рассмотрения дополнительных структур. [62]
Векторному пространству может быть задан частичный порядок , при котором некоторые векторы могут быть сравнены. [63] Например, -мерное действительное пространство может быть упорядочено путем сравнения его векторов покомпонентно. Упорядоченные векторные пространства , например, пространства Рисса , являются основополагающими для интегрирования Лебега , которое опирается на способность выражать функцию как разность двух положительных функций, где обозначает положительную часть и отрицательную часть. [64]
Нормированные векторные пространства и пространства внутренних произведений
«Измерение» векторов выполняется путем указания нормы , данных, которые измеряют длины векторов, или внутреннего произведения , которое измеряет углы между векторами. Нормы и внутренние произведения обозначаются и соответственно. Данные внутреннего произведения влекут за собой, что длины векторов также могут быть определены путем определения соответствующей нормы Векторные пространства, наделенные такими данными, известны как нормированные векторные пространства и пространства внутренних произведений , соответственно. [65]
Координатное пространство может быть снабжено стандартным скалярным произведением : В этом отражается общее понятие угла между двумя векторами и по закону косинусов : Из-за этого два вектора, удовлетворяющие , называются ортогональными . Важный вариант стандартного скалярного произведения используется в пространстве Минковского : наделено произведением Лоренца [66] В отличие от стандартного скалярного произведения, оно не является положительно определенным : также принимает отрицательные значения, например, для Выделение четвертой координаты — соответствующей времени , в отличие от трех пространственных измерений — делает ее полезной для математической обработки специальной теории относительности . Обратите внимание, что в других соглашениях время часто записывается как первый или «нулевой» компонент, так что произведение Лоренца записывается
Топологические векторные пространства
Вопросы сходимости решаются путем рассмотрения векторных пространств, несущих совместимую топологию , структуру, которая позволяет говорить об элементах, находящихся близко друг к другу . [67] Совместимость здесь означает, что сложение и скалярное умножение должны быть непрерывными отображениями . Грубо говоря, если и в , и в изменяются на ограниченную величину, то так же изменяются и [nb 6] Чтобы иметь смысл указывать величину, на которую изменяется скаляр, поле также должно нести топологию в этом контексте; распространенным выбором являются действительные или комплексные числа.
В таких топологических векторных пространствах можно рассматривать ряды векторов. Бесконечная сумма обозначает предел соответствующих конечных частичных сумм последовательности элементов Например, могут быть (действительными или комплексными) функциями, принадлежащими некоторому функциональному пространству , в этом случае ряд является функциональным рядом . Режим сходимости ряда зависит от топологии, наложенной на функциональное пространство. В таких случаях поточечная сходимость и равномерная сходимость являются двумя яркими примерами. [68]
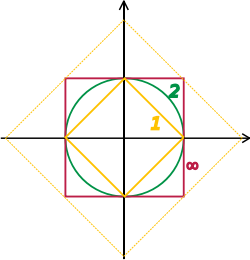
Способом обеспечения существования пределов некоторых бесконечных рядов является ограничение внимания пространствами, где любая последовательность Коши имеет предел; такое векторное пространство называется полным . Грубо говоря, векторное пространство является полным при условии, что оно содержит все необходимые пределы. Например, векторное пространство многочленов на единичном интервале, снабженное топологией равномерной сходимости, не является полным, поскольку любая непрерывная функция на может быть равномерно приближена последовательностью многочленов, по теореме об аппроксимации Вейерштрасса . [69] Напротив, пространство всех непрерывных функций на с той же топологией является полным. [70] Норма порождает топологию, определяя, что последовательность векторов сходится к тогда и только тогда, когда банахово и гильбертово пространства являются полными топологическими векторными пространствами, топологии которых задаются, соответственно, нормой и скалярным произведением. Их исследование — ключевая часть функционального анализа — фокусируется на бесконечномерных векторных пространствах, поскольку все нормы на конечномерных топологических векторных пространствах порождают одно и то же понятие сходимости. [71] Изображение справа показывает эквивалентность -нормы и -нормы на , поскольку единичные "шары" охватывают друг друга, последовательность сходится к нулю в одной норме тогда и только тогда, когда это происходит в другой норме. В бесконечномерном случае, однако, как правило, будут неэквивалентные топологии, что делает изучение топологических векторных пространств более богатым, чем изучение векторных пространств без дополнительных данных.
С концептуальной точки зрения все понятия, связанные с топологическими векторными пространствами, должны соответствовать топологии. Например, вместо рассмотрения всех линейных отображений (также называемых функционалами ) отображения между топологическими векторными пространствами должны быть непрерывными. [72] В частности, (топологическое) сопряженное пространство состоит из непрерывных функционалов (или к ). Основная теорема Хана–Банаха касается разделения подпространств соответствующих топологических векторных пространств непрерывными функционалами. [73]
Банаховы пространства
Банаховы пространства , введенные Стефаном Банахом , являются полными нормированными векторными пространствами. [74]
Первым примером является векторное пространство, состоящее из бесконечных векторов с действительными элементами, чья -норма задается выражением
Топологии на бесконечномерном пространстве неэквивалентны для разных Например, последовательность векторов, в которой первые компоненты — , а следующие — сходится к нулевому вектору при , но не сходится при , но
В более общем смысле, чем последовательности действительных чисел, функции наделены нормой, которая заменяет указанную выше сумму интегралом Лебега
Пространство интегрируемых функций на заданной области (например, интервале), удовлетворяющее этой норме и снабженное ею, называется пространством Лебега и обозначается [nb 7]
Эти пространства являются полными. [75] (Если вместо этого использовать интеграл Римана , пространство не является полным, что можно рассматривать как обоснование теории интегрирования Лебега. [nb 8] ) Конкретно это означает, что для любой последовательности функций, интегрируемых по Лебегу, удовлетворяющей условию, существует функция, принадлежащая векторному пространству, такая, что
Наложение условий ограниченности не только на функцию, но и на ее производные приводит к пространствам Соболева . [76]
Гильбертовы пространства

Полные пространства скалярного произведения известны как пространства Гильберта , в честь Дэвида Гильберта . [77] Гильбертово пространство со скалярным произведением, заданным как , где обозначает комплексное сопряжение [78] [примечание 9], является ключевым случаем.
По определению, в гильбертовом пространстве любая последовательность Коши сходится к пределу. И наоборот, нахождение последовательности функций с желаемыми свойствами, которые аппроксимируют заданную предельную функцию, столь же важно. Ранний анализ под видом приближения Тейлора установил приближение дифференцируемых функций полиномами. [79] По теореме Стоуна–Вейерштрасса каждая непрерывная функция на может быть аппроксимирована полиномом сколь угодно близко. [80] Похожий метод приближения тригонометрическими функциями обычно называется разложением Фурье и широко применяется в инженерии. В более общем смысле и более концептуально теорема дает простое описание того, какие «базисные функции» или, в абстрактных гильбертовых пространствах, какие базисные векторы достаточны для генерации гильбертова пространства в том смысле, что замыкание их диапазона (то есть конечных линейных комбинаций и их пределов) является всем пространством. Такой набор функций называется базисом , его мощность известна как размерность гильбертова пространства . [nb 10] Теорема не только демонстрирует подходящие базисные функции, достаточные для целей аппроксимации, но также вместе с процессом Грама-Шмидта позволяет построить базис ортогональных векторов . [81] Такие ортогональные базисы являются обобщением осей координат в конечномерном евклидовом пространстве на гильбертово пространство .
Решения различных дифференциальных уравнений можно интерпретировать в терминах гильбертовых пространств. Например, очень много областей в физике и технике приводят к таким уравнениям, и часто решения с определенными физическими свойствами используются в качестве базисных функций, часто ортогональных. [82] В качестве примера из физики, зависящее от времени уравнение Шредингера в квантовой механике описывает изменение физических свойств во времени с помощью частного дифференциального уравнения , решения которого называются волновыми функциями . [83] Определенные значения для физических свойств, таких как энергия или импульс, соответствуют собственным значениям определенного (линейного) дифференциального оператора , а связанные волновые функции называются собственными состояниями . Спектральная теорема разлагает линейный компактный оператор, действующий на функции, в терминах этих собственных функций и их собственных значений. [84]
Алгебры над полями

Общие векторные пространства не обладают умножением между векторами. Векторные пространства, снабженные дополнительным билинейным оператором, определяющим умножение двух векторов, являются алгеброй над полем (или F -алгеброй, если поле F указано). [85]
Например, множество всех многочленов образует алгебру, известную как кольцо многочленов : используя то, что сумма двух многочленов является многочленом, они образуют векторное пространство; они образуют алгебру, поскольку произведение двух многочленов снова является многочленом. Кольца многочленов (от нескольких переменных) и их частных образуют основу алгебраической геометрии , поскольку они являются кольцами функций алгебраических геометрических объектов . [86]
Другим важным примером являются алгебры Ли , которые не являются ни коммутативными, ни ассоциативными, но неспособность быть таковыми ограничена ограничениями ( обозначает произведение и ):
- ( антикоммутативность ) и
- ( тождество Якоби ). [87]
Примерами служат векторное пространство матриц типа -by- с коммутатором двух матриц, снабженное векторным произведением .
Тензорная алгебра — это формальный способ сложения произведений в любое векторное пространство для получения алгебры. [88] Как векторное пространство, оно охватывается символами, называемыми простыми тензорами , где степень варьируется. Умножение задается путем конкатенации таких символов, наложения закона распределения при сложении и требования, чтобы скалярное умножение коммутировало с тензорным произведением ⊗, во многом так же, как и с тензорным произведением двух векторных пространств, введенным в предыдущем разделе о тензорных произведениях. В общем случае нет никаких соотношений между и Принуждение двух таких элементов к равенству приводит к симметричной алгебре , тогда как принуждение дает внешнюю алгебру . [89]
Связанные структуры
Векторные пучки

Векторным расслоением называется семейство векторных пространств, непрерывно параметризованных топологическим пространством X. [90] Точнее, векторным расслоением над X называется топологическое пространство E, снабженное непрерывным отображением, таким, что для каждого x из X волокно π−1 ( x ) является векторным пространством . Случай dim V = 1 называется линейным расслоением . Для любого векторного пространства V проекция X × V → X превращает произведение X × V в «тривиальное» векторное расслоение . Векторные расслоения над X должны быть локально произведением X и некоторого (фиксированного) векторного пространства V : для каждого x из X существует окрестность U x такая, что ограничение π до π −1 ( U ) изоморфно [nb 11] тривиальному расслоению U × V → U . Несмотря на их локально тривиальный характер, векторные расслоения могут (в зависимости от формы базового пространства X ) быть «скрученными» в целом (то есть расслоение не обязательно должно быть (глобально изоморфным) тривиальному расслоению X × V ). Например, ленту Мёбиуса можно рассматривать как линейное расслоение над окружностью S 1 (путем отождествления открытых интервалов с действительной прямой ). Однако оно отличается от цилиндра S 1 × R , поскольку последний является ориентируемым, а первый — нет. [91]
Свойства некоторых векторных расслоений предоставляют информацию о базовом топологическом пространстве. Например, касательное расслоение состоит из набора касательных пространств, параметризованных точками дифференцируемого многообразия. Касательное расслоение окружности S 1 глобально изоморфно S 1 × R , поскольку на S 1 существует глобальное ненулевое векторное поле . [nb 12] Напротив, по теореме о волосатом шаре не существует (касательного) векторного поля на 2-сфере S 2 , которое было бы всюду ненулевым. [92] K-теория изучает классы изоморфизма всех векторных расслоений над некоторым топологическим пространством. [93] Помимо углубления топологического и геометрического понимания, оно имеет чисто алгебраические следствия, такие как классификация конечномерных вещественных алгебр с делением : R , C , кватернионы H и октонионы O .
Кокасательное расслоение дифференцируемого многообразия состоит в каждой точке многообразия из сопряженного касательного пространства, кокасательного пространства . Сечения этого расслоения известны как дифференциальные формы .
Модули
Модули являются для колец тем же, чем векторные пространства являются для полей: те же аксиомы, примененные к кольцу R вместо поля F , дают модули. [94] Теория модулей, по сравнению с теорией векторных пространств, усложняется наличием элементов кольца, которые не имеют мультипликативных обратных . Например, модули не обязательно должны иметь базы, как показывает Z -модуль (то есть абелева группа ) Z /2 Z ; те модули, которые имеют (включая все векторные пространства), известны как свободные модули . Тем не менее, векторное пространство можно компактно определить как модуль над кольцом , которое является полем , причем элементы называются векторами. Некоторые авторы используют термин векторное пространство для обозначения модулей над телом . [95] Алгебро-геометрическая интерпретация коммутативных колец через их спектр позволяет разрабатывать такие концепции, как локально свободные модули , алгебраический аналог векторных расслоений.
Аффинные и проективные пространства
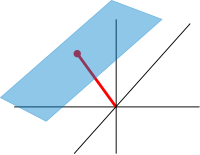
Грубо говоря, аффинные пространства — это векторные пространства, начала координат которых не указаны. [96] Точнее, аффинное пространство — это множество со свободным транзитивным действием векторного пространства . В частности, векторное пространство — это аффинное пространство над собой, с помощью отображения Если W — векторное пространство, то аффинное подпространство — это подмножество W, полученное путем переноса линейного подпространства V на фиксированный вектор x ∈ W ; это пространство обозначается как x + V (оно является смежным классом V в W ) и состоит из всех векторов вида x + v для v ∈ V . Важным примером является пространство решений системы неоднородных линейных уравнений, обобщающее однородный случай, обсуждаемый в предыдущем разделе о линейных уравнениях, который можно найти, положив в этом уравнении. [97] Пространство решений — это аффинное подпространство x + V , где x — частное решение уравнения, а V — пространство решений однородного уравнения ( нулевое пространство A ) .
Множество одномерных подпространств фиксированного конечномерного векторного пространства V известно как проективное пространство ; его можно использовать для формализации идеи параллельных линий, пересекающихся на бесконечности. [98] Грассманианы и флаговые многообразия обобщают это, параметризуя линейные подпространства фиксированной размерности k и флаги подпространств соответственно.
Примечания
- ^ Также принято, особенно в физике, обозначать векторы стрелкой сверху: Также принято, особенно в высшей математике, не использовать никаких типографских методов для различения векторов от других математических объектов.
- ^ Скалярное умножение не следует путать со скалярным произведением , которое является дополнительной операцией в некоторых конкретных векторных пространствах, называемых пространствами внутреннего произведения . Скалярное умножение — это умножение вектора на скаляр, которое дает вектор, в то время как скалярное произведение — это умножение двух векторов, которое дает скаляр.
- ^ Эта аксиома не является ассоциативным свойством , поскольку относится к двум разным операциям: скалярному умножению и умножению полей. Таким образом, она независима от ассоциативности умножения полей, которая предполагается аксиомами полей.
- ^ Это обычно имеет место, когда векторное пространство также рассматривается как аффинное пространство . В этом случае линейное подпространство содержит нулевой вектор , тогда как аффинное подпространство не обязательно его содержит.
- ^ Некоторые авторы, такие как Роман (2005), предпочитают начинать с этого отношения эквивалентности и выводить конкретную форму из него.
- ^ Это требование подразумевает, что топология приводит к однородной структуре , Бурбаки (1989), там же = гл. II.
- ^ Неравенство треугольника для обеспечивается неравенством Минковского . По техническим причинам в контексте функций необходимо определить функции, которые совпадают почти всюду, чтобы получить норму, а не только полунорму .
- ^ "Многие функции в мере Лебега, будучи неограниченными, не могут быть интегрированы с помощью классического интеграла Римана. Поэтому пространства интегрируемых по Риману функций не будут полными по норме, и ортогональное разложение к ним не будет применимо. Это показывает одно из преимуществ интегрирования по Лебегу.", Дадли (1989), §5.3, стр. 125.
- ^ Для не является гильбертовым пространством.
- ^ Базис гильбертова пространства — это не то же самое, что базис линейной алгебры. Для отличия базис линейной алгебры для гильбертова пространства называется базисом Гамеля .
- ^ То есть существует гомеоморфизм из π −1 ( U ) в V × U , который ограничивается линейными изоморфизмами между волокнами.
- ^ Линейное расслоение, такое как касательное расслоение S 1 , тривиально тогда и только тогда, когда существует сечение , которое нигде не обращается в нуль, см. Husemoller (1994), следствие 8.3. Сечения касательного расслоения являются просто векторными полями .
Цитаты
- ^ Ланг 2002.
- ^ Браун 1991, стр. 86.
- ↑ Роман 2005, гл. 1, стр. 27.
- ^ Браун 1991, стр. 87.
- ↑ Springer 2000, стр. 185; Brown 1991, стр. 86.
- ^ Атья и Макдональд 1969, стр. 17.
- ^ Бурбаки 1998, §1.1, Определение 2.
- ^ Браун 1991, стр. 94.
- ↑ Браун 1991, стр. 99–101.
- ^ Браун 1991, стр. 92.
- ^ ab Stoll & Wong 1968, стр. 14.
- ↑ Роман 2005, стр. 41–42.
- ^ Ланг 1987, с. 10–11; Антон и Роррес 2010, с. 212.
- ^ Бласс 1984.
- ^ Джоши 1989, стр. 450.
- ^ Хейл 2011, стр. 126.
- ↑ Халмош 1948, стр. 12.
- ^ Бурбаки 1969, гл. «Линейная и многолинейная алгебра», стр. 78–91.
- ↑ Больцано 1804.
- ↑ Мёбиус 1827.
- ^ Беллавитис 1833.
- ^ Дориер 1995.
- ↑ Гамильтон 1853.
- ^ Грассманн 2000.
- ↑ Пеано 1888, гл. IX.
- ^ Го 2021.
- ^ Мур 1995, стр. 268–271.
- ^ Банах 1922.
- ^ Дориер 1995; Мур 1995.
- ^ Крейсциг 2020, стр. 355.
- ^ Крейциг 2020, с. 358–359.
- ^ Джейн 2001, стр. 11.
- ^ Ланг 1987, гл. I.1.
- ^ Ланг 2002, гл. V.1.
- ^ Ланг 1993, гл. XII.3., с. 335.
- ^ Ланг 1987, гл. VI.3..
- ↑ Роман 2005, гл. 2, стр. 45.
- ^ Ланг 1987, гл. IV.4, Следствие, стр. 106.
- ^ Николсон 2018, гл. 7.3.
- ^ Ланг 1987, Пример IV.2.6.
- ^ Ланг 1987, гл. VI.6.
- ↑ Халмош 1974, стр. 28, пример 9.
- ^ Лэнг 1987, Теорема IV.2.1, стр. 95.
- ↑ Роман 2005, Ф. 2.5 и 2.6, стр. 49.
- ^ Ланг 1987, гл. V.1.
- ^ Ланг 1987, гл. V.3., Следствие, стр. 106.
- ^ Лэнг 1987, Теорема VII.9.8, стр. 198.
- ↑ Роман 2005, гл. 8, стр. 135–156.
- ^ & Lang 1987, гл. IX.4.
- ↑ Роман 2005, гл. 8, стр. 140.
- ↑ Роман 2005, гл. 1, стр. 29.
- ↑ Роман 2005, гл. 1, стр. 35.
- ^ Николсон 2018, гл. 10.4.
- ↑ Роман 2005, гл. 3, стр. 64.
- ^ Ланг 1987, гл. IV.3..
- ↑ Роман 2005, гл. 2, стр. 48.
- ^ Николсон 2018, гл. 7.4.
- ^ Мак Лейн 1998.
- ↑ Роман 2005, гл. 1, стр. 31–32.
- ^ Ланг 2002, гл. XVI.1.
- ^ Роман (2005), Т. 14.3. См. также лемму Йонеды .
- ^ Рудин 1991, стр.3.
- ^ Шефер и Вольф 1999, стр. 204–205.
- ^ Бурбаки 2004, гл. 2, с. 48.
- ↑ Роман 2005, гл. 9.
- ^ Набер 2003, гл. 1.2.
- ↑ Тревес 1967; Бурбаки 1987.
- ^ Шефер и Вольф 1999, стр. 7.
- ^ Крейсциг 1989, §4.11-5
- ^ Крейсциг 1989, §1.5-5
- ^ Шоке 1966, Предложение III.7.2.
- ↑ Тревес 1967, стр. 34–36.
- ↑ Лэнг 1983, Кор. 4.1.2, стр. 69.
- ↑ Тревес 1967, гл. 11.
- ^ Тревес 1967, Теорема 11.2, стр. 102.
- ↑ Эванс 1998, гл. 5.
- ↑ Тревес 1967, гл. 12.
- ^ Деннери и Кшивицкий 1996, стр.190.
- ^ Ланг 1993, Th. XIII.6, с. 349.
- ^ Ланг 1993, Т. III.1.1.
- ^ Шоке 1966, Лемма III.16.11.
- ^ Крейциг 1999, Глава 11.
- ↑ Гриффитс 1995, Глава 1.
- ↑ Ланг 1993, гл. XVII.3.
- ^ Ланг 2002, гл. III.1, стр. 121.
- ^ Эйзенбуд 1995, гл. 1.6.
- ^ Варадараджан 1974.
- ↑ Ланг 2002, гл. XVI.7.
- ^ Ланг 2002, гл. XVI.8.
- ↑ Спивак 1999, гл. 3.
- ^ Крейциг 1991, §34, с. 108.
- ^ Эйзенберг и Гай 1979.
- ^ Атья 1989.
- ↑ Артин 1991, гл. 12.
- ^ Гриле 2007.
- ^ Мейер 2000, Пример 5.13.5, стр. 436.
- ^ Мейер 2000, Упражнение 5.13.15–17, стр. 442.
- ^ Коксетер 1987.
Ссылки
Алгебра
- Антон, Говард; Роррес, Крис (2010), Элементарная линейная алгебра: версия приложений (10-е изд.), John Wiley & Sons
- Артин, Майкл (1991), Алгебра , Прентис Холл , ISBN 978-0-89871-510-1
- Браун, Уильям А. (1991), Матрицы и векторные пространства , Нью-Йорк: М. Деккер, ISBN 978-0-8247-8419-5
- Грийе, Пьер Антуан (2007), Абстрактная алгебра , Graduate Texts in Mathematics, т. 242, Springer Science & Business Media, doi : 10.1007/978-0-387-71568-1, ISBN 978-0-387-71568-1
- Халмош, Пол Р. (1948), Конечномерные векторные пространства , т. 7, Princeton University Press
- Хейл, Кристофер (2011), Учебник базовой теории: расширенное издание , прикладной и численный гармонический анализ, Биркхойзер, doi : 10.1007/978-0-8176-4687-5, ISBN 978-0-8176-4687-5
- Джейн, М.С. (2001), Векторные пространства и матрицы в физике, CRC Press, ISBN 978-0-8493-0978-6
- Джоши, К.Д. (1989), Основы дискретной математики , John Wiley & Sons
- Крейциг, Эрвин (2020), Высшая инженерная математика, John Wiley & Sons, ISBN 978-1-119-45592-9
- Ланг, Серж (1987), Линейная алгебра , Тексты для бакалавров по математике (3-е изд.), Springer, doi :10.1007/978-1-4757-1949-9, ISBN 978-1-4757-1949-9
- Ланг, Серж (2002), Алгебра , Graduate Texts in Mathematics , т. 211 (пересмотренное третье издание), Нью-Йорк: Springer-Verlag, ISBN 978-0-387-95385-4, г-н 1878556
- Mac Lane, Saunders (1999), Алгебра (3-е изд.), Американское математическое общество, стр. 193–222 , ISBN 978-0-8218-1646-2
- Мейер, Карл Д. (2000), Матричный анализ и прикладная линейная алгебра, SIAM , ISBN 978-0-89871-454-8
- Николсон, В. Кит (2018), Линейная алгебра с приложениями, Lyryx
- Роман, Стивен (2005), Продвинутая линейная алгебра , Graduate Texts in Mathematics, т. 135 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-24766-3
- Шпиндлер, Карлхайнц (1993), Абстрактная алгебра с приложениями: Том 1: Векторные пространства и группы , CRC, ISBN 978-0-8247-9144-5
- Springer, TA (2000), Линейные алгебраические группы, Springer, ISBN 978-0-8176-4840-4
- Столл, Р.Р.; Вонг, Э.Т. (1968), Линейная алгебра , Academic Press
- ван дер Варден, Бартель Леендерт (1993), Алгебра (на немецком языке) (9-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-56799-8
Анализ
- Бурбаки, Николя (1987), Топологические векторные пространства , Элементы математики, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-13627-9
- Бурбаки, Николя (2004), Интеграция I , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-41129-1
- Браун, Мартин (1993), Дифференциальные уравнения и их приложения: введение в прикладную математику , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-97894-9
- BSE-3 (2001) [1994], "Касательная плоскость", Энциклопедия математики , EMS Press
- Шоке, Гюстав (1966), Топология , Бостон, Массачусетс: Academic Press
- Деннери, Филипп; Крживицкий, Андре (1996), Математика для физиков , Courier Dover Publications, ISBN 978-0-486-69193-0
- Дадли, Ричард М. (1989), Действительный анализ и вероятность , Математическая серия Уодсворта и Брукса/Коула, Пасифик-Гроув, Калифорния: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6
- Данэм, Уильям (2005), Галерея исчисления , Издательство Принстонского университета , ISBN 978-0-691-09565-3
- Эванс, Лоуренс К. (1998), Уравнения с частными производными , Провиденс, Род-Айленд: Американское математическое общество , ISBN 978-0-8218-0772-9
- Фолланд, Джеральд Б. (1992), Анализ Фурье и его приложения , Brooks-Cole, ISBN 978-0-534-17094-3
- Гаске, Клод; Витомски, Патрик (1999), Анализ Фурье и его применение: фильтрация, численные вычисления, вейвлеты , Тексты по прикладной математике, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-98485-8
- Айфичор, Эммануэль К.; Джервис, Барри В. (2001), Цифровая обработка сигналов: практический подход (2-е изд.), Харлоу, Эссекс, Англия: Prentice-Hall (опубликовано в 2002 г.), ISBN 978-0-201-59619-9
- Кранц, Стивен Г. (1999), Панорама гармонического анализа , Carus Mathematical Monographs, Вашингтон, округ Колумбия: Математическая ассоциация Америки, ISBN 978-0-88385-031-2
- Крейциг, Эрвин (1988), Advanced Engineering Mathematics (6-е изд.), Нью-Йорк: John Wiley & Sons, ISBN 978-0-471-85824-9
- Крейциг, Эрвин (1989), Вводный функциональный анализ с приложениями , Wiley Classics Library, Нью-Йорк: John Wiley & Sons , ISBN 978-0-471-50459-7, МР 0992618
- Ланг, Серж (1983), Реальный анализ , Эддисон-Уэсли , ISBN 978-0-201-14179-5
- Ланг, Серж (1993), Действительный и функциональный анализ , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-94001-4
- Лумис, Линн Х. (2011) [1953], Введение в абстрактный гармонический анализ , Довер, hdl : 2027/uc1.b4250788 , ISBN 978-0-486-48123-4, OCLC 702357363
- Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Рудин, Уолтер (1991), Функциональный анализ (2-е изд.), McGraw-Hill, ISBN 0070542368
- Шефер, Хельмут Х.; Вольф, Манфред П. (1999). Топологические векторные пространства . GTM . Том 8 (Второе издание). Нью-Йорк, Нью-Йорк: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Тревес, Франсуа (1967), Топологические векторные пространства, распределения и ядра , Бостон, Массачусетс: Academic Press
Исторические справки
- Банах, Стефан (1922), «Sur les opérations dans les ансамбли abstraits et leur application aux équations intégrales (Об операциях в абстрактных множествах и их применении к интегральным уравнениям)» (PDF) , Fundamenta Mathematicae (на французском языке), 3 : 133– 181, дои :10.4064/fm-3-1-133-181, ISSN 0016-2736
- Больцано, Бернар (1804 г.), Betrachtungen über einige Gegenstände der Elementargeometrie (Соображения некоторых аспектов элементарной геометрии) (на немецком языке)
- Беллавитис, Джузо (1833), «Sopra alcune applicazioni di un nuovo metodo di geometria analitica», Il poligrafo giornale di Science, lettre ed arti , 13 , Верона: 53–61.
- Бурбаки, Николя (1969), Éléments d'histoire des mathématiques (Элементы истории математики) (на французском языке), Париж: Герман
- Дорье, Жан-Люк (1995), «Общий очерк генезиса теории векторного пространства», Historia Mathematica , 22 (3): 227–261 , doi : 10.1006/hmat.1995.1024 , MR 1347828
- Фурье, Жан Батист Жозеф (1822), Аналитическая теория (на французском языке), Chez Firmin Didot, père et fils
- Грассманн, Герман (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (на немецком языке), О. Виганд, перепечатка: Grassmann, Hermann (2000), Kannenberg, LC (ред.), Extension Theory , перевод Kannenberg, Lloyd C., Providence, RI: American Mathematical Society , ISBN 978-0-8218-2031-5
- Го, Хунъюй (2021-06-16), Что такое тензоры?, World Scientific, ISBN 978-981-12-4103-1
- Гамильтон, Уильям Роуэн (1853), Лекции о кватернионах, Королевская Ирландская академия
- Мёбиус, Август Фердинанд (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Барицентрическое исчисление: новая утилита для аналитической обработки геометрии) (на немецком языке), заархивировано из оригинала 23 ноября 2006 г.
- Мур, Грегори Х. (1995), «Аксиоматизация линейной алгебры: 1875–1940», Historia Mathematica , 22 (3): 262–303 , doi : 10.1006/hmat.1995.1025
- Пеано, Джузеппе (1888), Calcolo Geometrico Secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (на итальянском языке), Турин
{{citation}}: CS1 maint: location missing publisher (link) - Пеано, Г. (1901) Formulario mathematico : аксиомы vct, через Интернет-архив.
Дополнительные ссылки
- Эшкрофт, Нил ; Мермин, Н. Дэвид (1976), Физика твердого тела , Торонто: Thomson Learning, ISBN 978-0-03-083993-1
- Атья, Майкл Фрэнсис (1989), K-теория , Advanced Book Classics (2-е изд.), Addison-Wesley , ISBN 978-0-201-09394-0, МР 1043170
- Атья, Майкл Фрэнсис ; Макдональд, Ян Грант (1969), Введение в коммутативную алгебру , Advanced Book Classics, Addison-Wesley
- Бласс, Андреас (1984), «Существование баз подразумевает аксиому выбора» (PDF) , Аксиоматическая теория множеств , Contemporary Mathematics, том 31, Провиденс, Род-Айленд: Американское математическое общество , стр. 31–33 , ISBN 978-0-8218-5026-8, МР 0763890
- Бурбаки, Николас (1998), Элементы математики: Алгебра I Главы 1-3 , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-64243-5
- Бурбаки, Николас (1989), Общая топология. Главы 1-4 , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-64241-1
- Коксетер, Гарольд Скотт Макдональд (1987), Проективная геометрия (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-96532-1
- Эйзенберг, Мюррей; Гай, Роберт (1979), «Доказательство теоремы о волосатом шаре», The American Mathematical Monthly , 86 (7): 572– 574, doi :10.2307/2320587, JSTOR 2320587
- Эйзенбуд, Дэвид (1995), Коммутативная алгебра , Graduate Texts in Mathematics, т. 150, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-94269-8, г-н 1322960
- Голдрей, Дерек (1996), Классическая теория множеств: Управляемое независимое исследование (1-е изд.), Лондон: Chapman and Hall , ISBN 978-0-412-60610-6
- Гриффитс, Дэвид Дж. (1995), Введение в квантовую механику , Аппер Сэддл Ривер, Нью-Джерси: Prentice Hall , ISBN 978-0-13-124405-4
- Халмош, Пол Р. (1974), Конечномерные векторные пространства , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-90093-3
- Халперн, Джеймс Д. (июнь 1966 г.), «Базисы в векторных пространствах и аксиома выбора», Труды Американского математического общества , 17 (3): 670– 673, doi : 10.2307/2035388 , JSTOR 2035388
- Хьюз-Халлетт, Дебора; МакКаллум, Уильям Г.; Глисон, Эндрю М. (2013), Исчисление: одно- и многомерное (6-е изд.), John Wiley & Sons , ISBN 978-0470-88861-2
- Хуземоллер, Дейл (1994), Fiber Bundles (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-94087-8
- Йост, Юрген (2005), Риманова геометрия и геометрический анализ (4-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-25907-7
- Крейциг, Эрвин (1991), Дифференциальная геометрия , Нью-Йорк: Dover Publications , стр. xiv+352, ISBN 978-0-486-66721-8
- Крейциг, Эрвин (1999), Advanced Engineering Mathematics (8-е изд.), Нью-Йорк: John Wiley & Sons , ISBN 978-0-471-15496-9
- Люенбергер, Дэвид (1997), Оптимизация методами векторного пространства , Нью-Йорк: John Wiley & Sons , ISBN 978-0-471-18117-0
- Mac Lane, Saunders (1998), Категории для работающего математика (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-98403-2
- Мизнер, Чарльз В.; Торн , Кип ; Уилер, Джон Арчибальд (1973), Гравитация , WH Freeman, ISBN 978-0-7167-0344-0
- Набер, Грегори Л. (2003), Геометрия пространства-времени Минковского , Нью-Йорк: Dover Publications , ISBN 978-0-486-43235-9, г-н 2044239
- Шенхаге, А .; Штрассен, Фолькер (1971), «Schnelle Multiplikation großer Zahlen (Быстрое умножение больших чисел)», Computing (на немецком языке), 7 ( 3–4 ): 281–292 , doi : 10.1007/bf02242355, ISSN 0010-485X, S2CID 9738629
- Спивак, Майкл (1999), Всестороннее введение в дифференциальную геометрию (том второй) , Хьюстон, Техас: Опубликуй или погибни
- Стюарт, Ян (1975), Теория Галуа , Математическая серия Чепмена и Холла , Лондон: Чепмен и Холл , ISBN 978-0-412-10800-6
- Варадараджан, В.С. (1974), Группы Ли, алгебры Ли и их представления , Prentice Hall , ISBN 978-0-13-535732-3
- Уоллес, Г. К. (февраль 1992 г.), «Стандарт сжатия неподвижных изображений JPEG» (PDF) , IEEE Transactions on Consumer Electronics , 38 (1): xviii– xxxiv, CiteSeerX 10.1.1.318.4292 , doi :10.1109/30.125072, ISSN 0098-3063, архивировано из оригинала (PDF) 13.01.2007 г. , извлечено 25.10.2017 г.
- Weibel, Charles A. (1994). Введение в гомологическую алгебру . Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.
Внешние ссылки
- «Векторное пространство», Энциклопедия математики , EMS Press , 2001 [1994]












































































































































![{\displaystyle [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/971caee396752d8bf56711f55d2c3b1207d4a236)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)







































![{\displaystyle [а,б]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle \mathbf {R} [x,y]/(x\cdot y-1),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ba7424ec2e6bf0fc108cb223ae2d6209c67b44d)


![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)


![{\displaystyle [x,y]=-[y,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f70fcda86c14de45e211c3a9a889845038bb7348)
![{\displaystyle [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23655a62f2a7cc545f121d9bcc30fe2c56731457)
![{\displaystyle [x,y]=xy-yx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c9d7bc98d1738f549c0420244c08c57decc66b3)















