Распределительная собственность

Распределительная собственность

Визуализация закона распределения для положительных чисел
Тип	Закон , правило замены
Поле	Элементарная алгебра Булева алгебра Абстрактная алгебра Теория множеств Пропозициональное исчисление
Символическое заявление	Элементарная алгебра $${\displaystyle x\cdot (y+z)=x\cdot y+x\cdot z}$$ Пропозициональное исчисление: ${\displaystyle (P\land (Q\lor R))\Leftrightarrow ((P\land Q)\lor (P\land R))}$ ${\displaystyle (P\lor (Q\land R))\Leftrightarrow ((P\lor Q)\land (P\lor R))}$

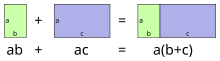
В математике распределительное свойство бинарных операций является обобщением распределительного закона , который утверждает, что равенство всегда истинно в элементарной алгебре . Например, в элементарной арифметике , можно сказать, что поэтому умножение распределяется относительно сложения .$${\displaystyle x\cdot (y+z)=x\cdot y+x\cdot z}$$$${\displaystyle 2\cdot (1+3)=(2\cdot 1)+(2\cdot 3).}$$

Это основное свойство чисел является частью определения большинства алгебраических структур , которые имеют две операции, называемые сложением и умножением, такие как комплексные числа , многочлены , матрицы , кольца и поля . Оно также встречается в булевой алгебре и математической логике , где каждое из логического и (обозначается ) и логического или (обозначается ) распределяется по другому.${\displaystyle \,\land \,}$${\displaystyle \,\lor \,}$

Дан набор и два бинарных оператора и на${\displaystyle S}$ ${\displaystyle \,*\,}$${\displaystyle \,+\,}$${\displaystyle S,}$

• операция является лево-дистрибутивной по (или относительно), если, учитывая любые элементы${\displaystyle \,*\,}$${\displaystyle \,+\,}$${\displaystyle x,y,{\text{ and }}z}$${\displaystyle S,}$

$${\displaystyle x*(y+z)=(x*y)+(x*z);}$$

• операция является правораспределительной , если, учитывая любые элементы${\displaystyle \,*\,}$${\displaystyle \,+\,}$${\displaystyle x,y,{\text{ and }}z}$${\displaystyle S,}$

$${\displaystyle (y+z)*x=(y*x)+(z*x);}$$

• и операция является дистрибутивной , если она является дистрибутивной слева и справа. ^[1]${\displaystyle \,*\,}$${\displaystyle \,+\,}$

Если является коммутативным , три приведенных выше условия логически эквивалентны .${\displaystyle \,*\,}$

Операторы, используемые в примерах в этом разделе, являются обычными операторами сложения и умножения.${\displaystyle \,+\,}$ ${\displaystyle \,\cdot .\,}$

Если обозначенная операция не является коммутативной, то существует различие между левой дистрибутивностью и правой дистрибутивностью:${\displaystyle \cdot }$

$${\displaystyle a\cdot \left(b\pm c\right)=a\cdot b\pm a\cdot c\qquad {\text{ (left-distributive) }}}$$$${\displaystyle (a\pm b)\cdot c=a\cdot c\pm b\cdot c\qquad {\text{ (right-distributive) }}.}$$

В любом случае распределительное свойство можно описать словами как:

Чтобы умножить сумму (или разность ) на множитель, каждое слагаемое (или уменьшаемое и вычитаемое ) умножается на этот множитель, а полученные произведения складываются (или вычитаются).

Если операция вне скобок (в данном случае умножение) коммутативна, то левая дистрибутивность подразумевает правую дистрибутивность и наоборот, и говорят просто о дистрибутивности .

Одним из примеров операции, которая является «только» право-дистрибутивной, является деление, которое не является коммутативным: В этом случае лево-дистрибутивность не применяется:$${\displaystyle (a\pm b)\div c=a\div c\pm b\div c.}$$$${\displaystyle a\div (b\pm c)\neq a\div b\pm a\div c}$$

Дистрибутивные законы входят в число аксиом для колец (например, кольца целых чисел ) и полей (например, поля рациональных чисел ). Здесь умножение дистрибутивно относительно сложения, но сложение не дистрибутивно относительно умножения. Примерами структур с двумя операциями, каждая из которых дистрибутивна относительно другой, являются булевы алгебры, такие как алгебра множеств или алгебра переключения .

Умножение сумм можно выразить словами следующим образом: когда сумма умножается на сумму, умножьте каждое слагаемое одной суммы на каждое слагаемое другой суммы (следя за знаками), затем сложите все полученные произведения.

В следующих примерах иллюстрируется применение закона распределения на множестве действительных чисел . Когда в элементарной математике упоминается умножение, обычно имеется в виду именно этот вид умножения. С точки зрения алгебры действительные числа образуют поле , которое обеспечивает справедливость закона распределения.${\displaystyle \mathbb {R} }$

Первый пример (умножение в уме и письменно)

При устном счете распределительность часто используется неосознанно: так, для того чтобы сделать расчет в уме, сначала умножают и и складывают промежуточные результаты. Письменное умножение также основано на распределительном законе.$${\displaystyle 6\cdot 16=6\cdot (10+6)=6\cdot 10+6\cdot 6=60+36=96}$$${\displaystyle 6\cdot 16}$${\displaystyle 6\cdot 10}$${\displaystyle 6\cdot 6}$

Второй пример (с переменными)

$${\displaystyle 3a^{2}b\cdot (4a-5b)=3a^{2}b\cdot 4a-3a^{2}b\cdot 5b=12a^{3}b-15a^{2}b^{2}}$$

Третий пример (с двумя суммами)

$${\displaystyle {\begin{aligned}(a+b)\cdot (a-b)&=a\cdot (a-b)+b\cdot (a-b)=a^{2}-ab+ba-b^{2}=a^{2}-b^{2}\\&=(a+b)\cdot a-(a+b)\cdot b=a^{2}+ba-ab-b^{2}=a^{2}-b^{2}\\\end{aligned}}}$$Здесь распределительный закон был применен дважды, и не имеет значения, какая скобка умножается первой.

Четвертый пример

Здесь распределительный закон применяется наоборот по сравнению с предыдущими примерами. Рассмотрим Поскольку множитель встречается во всех слагаемых, его можно вынести за скобки. То есть, в силу распределительного закона получаем$${\displaystyle 12a^{3}b^{2}-30a^{4}bc+18a^{2}b^{3}c^{2}\,.}$$${\displaystyle 6a^{2}b}$$${\displaystyle 12a^{3}b^{2}-30a^{4}bc+18a^{2}b^{3}c^{2}=6a^{2}b\left(2ab-5a^{2}c+3b^{2}c^{2}\right).}$$

Распределительный закон справедлив для умножения матриц . Точнее, для всех -матриц и -матриц , а также для всех -матриц и -матриц. Поскольку свойство коммутативности не выполняется для умножения матриц, второй закон не следует из первого закона. В этом случае это два разных закона.$${\displaystyle (A+B)\cdot C=A\cdot C+B\cdot C}$$${\displaystyle l\times m}$${\displaystyle A,B}$${\displaystyle m\times n}$${\displaystyle C,}$$${\displaystyle A\cdot (B+C)=A\cdot B+A\cdot C}$$${\displaystyle l\times m}$${\displaystyle A}$${\displaystyle m\times n}$${\displaystyle B,C.}$

• Умножение порядковых чисел , напротив, является только лево-дистрибутивным, а не право-дистрибутивным.
• Векторные произведения дистрибутивны слева и справа относительно сложения векторов , хотя и не коммутативны.
• Объединение множеств дистрибутивно относительно пересечения , а пересечение дистрибутивно относительно объединения.
• Логическая дизъюнкция («или») является дистрибутивной по отношению к логической конъюнкции («и»), и наоборот.
• Для действительных чисел (и для любого полностью упорядоченного множества ) операция максимума является распределительной относительно операции минимума , и наоборот:$${\displaystyle \max(a,\min(b,c))=\min(\max(a,b),\max(a,c))\quad {\text{ and }}\quad \min(a,\max(b,c))=\max(\min(a,b),\min(a,c)).}$$
• Для целых чисел наибольший общий делитель дистрибутивен по наименьшему общему кратному , и наоборот:$${\displaystyle \gcd(a,\operatorname {lcm} (b,c))=\operatorname {lcm} (\gcd(a,b),\gcd(a,c))\quad {\text{ and }}\quad \operatorname {lcm} (a,\gcd(b,c))=\gcd(\operatorname {lcm} (a,b),\operatorname {lcm} (a,c)).}$$
• Для действительных чисел сложение распределяется по максимальной операции, а также по минимальной операции:$${\displaystyle a+\max(b,c)=\max(a+b,a+c)\quad {\text{ and }}\quad a+\min(b,c)=\min(a+b,a+c).}$$
• Для биномиального умножения распределение иногда называют методом FOIL ^[2] (первые члены — внешний, внутренние и последние ), например:${\displaystyle ac,}$${\displaystyle ad,}$${\displaystyle bc,}$${\displaystyle bd}$${\displaystyle (a+b)\cdot (c+d)=ac+ad+bc+bd.}$
• Во всех полукольцах , включая комплексные числа , кватернионы , многочлены и матрицы , умножение распределяется относительно сложения:${\displaystyle u(v+w)=uv+uw,(u+v)w=uw+vw.}$
• Во всех алгебрах над полем , включая октонионы и другие неассоциативные алгебры , умножение распределяется относительно сложения.

В стандартной истинностно-функциональной пропозициональной логике распределение ^{[3] [4]} в логических доказательствах использует два допустимых правила замены для расширения отдельных вхождений определенных логических связок в пределах некоторой формулы в отдельные применения этих связок по подформулам данной формулы. Правила таковы , где " ", также записанный как металогический символ, представляющий "может быть заменено в доказательстве на" или " логически эквивалентно ".$${\displaystyle (P\land (Q\lor R))\Leftrightarrow ((P\land Q)\lor (P\land R))\qquad {\text{ and }}\qquad (P\lor (Q\land R))\Leftrightarrow ((P\lor Q)\land (P\lor R))}$$${\displaystyle \Leftrightarrow }$${\displaystyle \,\equiv ,\,}$

Дистрибутивность является свойством некоторых логических связок истинностно-функциональной пропозициональной логики . Следующие логические эквивалентности показывают, что дистрибутивность является свойством конкретных связок. Ниже приведены истинностно-функциональные тавтологии .$${\displaystyle {\begin{alignedat}{13}&(P&&\;\land &&(Q\lor R))&&\;\Leftrightarrow \;&&((P\land Q)&&\;\lor (P\land R))&&\quad {\text{ Distribution of }}&&{\text{ conjunction }}&&{\text{ over }}&&{\text{ disjunction }}\\&(P&&\;\lor &&(Q\land R))&&\;\Leftrightarrow \;&&((P\lor Q)&&\;\land (P\lor R))&&\quad {\text{ Distribution of }}&&{\text{ disjunction }}&&{\text{ over }}&&{\text{ conjunction }}\\&(P&&\;\land &&(Q\land R))&&\;\Leftrightarrow \;&&((P\land Q)&&\;\land (P\land R))&&\quad {\text{ Distribution of }}&&{\text{ conjunction }}&&{\text{ over }}&&{\text{ conjunction }}\\&(P&&\;\lor &&(Q\lor R))&&\;\Leftrightarrow \;&&((P\lor Q)&&\;\lor (P\lor R))&&\quad {\text{ Distribution of }}&&{\text{ disjunction }}&&{\text{ over }}&&{\text{ disjunction }}\\&(P&&\to &&(Q\to R))&&\;\Leftrightarrow \;&&((P\to Q)&&\to (P\to R))&&\quad {\text{ Distribution of }}&&{\text{ implication }}&&{\text{ }}&&{\text{ }}\\&(P&&\to &&(Q\leftrightarrow R))&&\;\Leftrightarrow \;&&((P\to Q)&&\leftrightarrow (P\to R))&&\quad {\text{ Distribution of }}&&{\text{ implication }}&&{\text{ over }}&&{\text{ equivalence }}\\&(P&&\to &&(Q\land R))&&\;\Leftrightarrow \;&&((P\to Q)&&\;\land (P\to R))&&\quad {\text{ Distribution of }}&&{\text{ implication }}&&{\text{ over }}&&{\text{ conjunction }}\\&(P&&\;\lor &&(Q\leftrightarrow R))&&\;\Leftrightarrow \;&&((P\lor Q)&&\leftrightarrow (P\lor R))&&\quad {\text{ Distribution of }}&&{\text{ disjunction }}&&{\text{ over }}&&{\text{ equivalence }}\\\end{alignedat}}}$$

Двойное распределение

$${\displaystyle {\begin{alignedat}{13}&((P\land Q)&&\;\lor (R\land S))&&\;\Leftrightarrow \;&&(((P\lor R)\land (P\lor S))&&\;\land ((Q\lor R)\land (Q\lor S)))&&\\&((P\lor Q)&&\;\land (R\lor S))&&\;\Leftrightarrow \;&&(((P\land R)\lor (P\land S))&&\;\lor ((Q\land R)\lor (Q\land S)))&&\\\end{alignedat}}}$$

В приближенной арифметике, такой как арифметика с плавающей точкой , распределительное свойство умножения (и деления) по сравнению со сложением может не выполняться из-за ограничений арифметической точности . Например, тождество не выполняется в десятичной арифметике , независимо от количества значимых цифр . Такие методы, как банковское округление, могут помочь в некоторых случаях, как и повышение используемой точности, но в конечном итоге некоторые ошибки в вычислениях неизбежны.${\displaystyle 1/3+1/3+1/3=(1+1+1)/3}$

Дистрибутивность чаще всего встречается в полукольцах , особенно в частных случаях колец и дистрибутивных решеток .

Полукольцо имеет две бинарные операции, обычно обозначаемые и , и требует, чтобы они распределялись по${\displaystyle \,+\,}$${\displaystyle \,*,}$${\displaystyle \,*\,}$${\displaystyle \,+.}$

Кольцо — это полукольцо с аддитивными обратными.

Решетка — это другой вид алгебраической структуры с двумя бинарными операциями. Если любая из этих операций распределяется по другой (скажем, распределяется по ), то обратное также имеет место ( распределяется по ), и решетка называется дистрибутивной. См. также Дистрибутивность (теория порядка) .${\displaystyle \,\land {\text{ and }}\lor .}$${\displaystyle \,\land \,}$${\displaystyle \,\lor }$${\displaystyle \,\lor \,}$${\displaystyle \,\land \,}$

Булева алгебра может быть интерпретирована либо как особый вид кольца ( булево кольцо ), либо как особый вид дистрибутивной решетки ( булева решетка ). Каждая интерпретация отвечает за различные дистрибутивные законы в булевой алгебре.

Аналогичные структуры без законов распределения — это почти кольца и почти поля вместо колец и делений . Операции обычно определяются как дистрибутивные справа, но не слева.

В нескольких областях математики рассматриваются обобщенные законы дистрибутивности. Это может включать ослабление вышеуказанных условий или расширение до бесконечных операций. Особенно в теории порядка можно найти многочисленные важные варианты дистрибутивности, некоторые из которых включают бесконечные операции, такие как бесконечный дистрибутивный закон ; другие определяются при наличии только одной бинарной операции, такие как соответствующие определения и их отношения даны в статье дистрибутивность (теория порядка) . Это также включает понятие полностью дистрибутивной решетки .

При наличии отношения порядка можно также ослабить приведенные выше равенства, заменив их на либо Естественно , это приведет к осмысленным концепциям только в некоторых ситуациях. Применением этого принципа является понятие субдистрибутивности, как объяснено в статье об интервальной арифметике .${\displaystyle \,=\,}$${\displaystyle \,\leq \,}$${\displaystyle \,\geq .}$

В теории категорий , если и являются монадами в категории, то закон дистрибутивности является естественным преобразованием , таким что является нестрогим отображением монад , а является колаксным отображением монад. Это именно те данные, которые необходимы для определения структуры монады в : отображение умножения равно , а отображение единиц равно См.: закон дистрибутивности между монадами .${\displaystyle (S,\mu ,\nu )}$${\displaystyle \left(S^{\prime },\mu ^{\prime },\nu ^{\prime }\right)}$ ${\displaystyle C,}$ ${\displaystyle S.S^{\prime }\to S^{\prime }.S}$ ${\displaystyle \lambda :S.S^{\prime }\to S^{\prime }.S}$${\displaystyle \left(S^{\prime },\lambda \right)}$ ${\displaystyle S\to S}$${\displaystyle (S,\lambda )}$ ${\displaystyle S^{\prime }\to S^{\prime }.}$${\displaystyle S^{\prime }.S}$${\displaystyle S^{\prime }\mu .\mu ^{\prime }S^{2}.S^{\prime }\lambda S}$${\displaystyle \eta ^{\prime }S.\eta .}$

В области теории информации был также предложен обобщенный распределительный закон .

Вездесущее тождество , связывающее обратные элементы с бинарной операцией в любой группе , а именно , которое принимается как аксиома в более общем контексте полугруппы с инволюцией , иногда называют антидистрибутивным свойством (инверсии как унарной операции ). ^[5]${\displaystyle (xy)^{-1}=y^{-1}x^{-1},}$

В контексте почти-кольца , которое устраняет коммутативность аддитивно записанной группы и предполагает только одностороннюю дистрибутивность, можно говорить о (двусторонних) дистрибутивных элементах , но также и об антидистрибутивных элементах . Последние меняют порядок (некоммутативного) сложения; предполагая левое сближение (т.е. такое, которое все элементы распределяют при умножении слева), тогда антидистрибутивный элемент меняет порядок сложения при умножении справа: ^[6]${\displaystyle a}$${\displaystyle (x+y)a=ya+xa.}$

При изучении пропозициональной логики и булевой алгебры термин «закон антидистрибутивности» иногда используется для обозначения взаимозамены между конъюнкцией и дизъюнкцией, когда над ними распространяется импликация: ^[7]$${\displaystyle (a\lor b)\Rightarrow c\equiv (a\Rightarrow c)\land (b\Rightarrow c)}$$$${\displaystyle (a\land b)\Rightarrow c\equiv (a\Rightarrow c)\lor (b\Rightarrow c).}$$

Эти две тавтологии являются прямым следствием двойственности законов Де Моргана .

Найдите понятие «дистрибутивность» в Викисловаре, бесплатном словаре.

• Демонстрация распределительного закона для целочисленной арифметики (из cut-the-knot )