Спектральная последовательность

Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Декабрь 2023 ) ( Узнайте, как и когда удалять это сообщение )

В гомологической алгебре и алгебраической топологии спектральная последовательность является средством вычисления групп гомологии с помощью последовательных приближений. Спектральные последовательности являются обобщением точных последовательностей , и с момента их введения Жаном Лере  (1946a, 1946b) они стали важными вычислительными инструментами, особенно в алгебраической топологии, алгебраической геометрии и гомологической алгебре.

Мотивированный проблемами алгебраической топологии, Жан Лере ввел понятие пучка и столкнулся с проблемой вычисления когомологий пучка . Для вычисления когомологий пучка Лере ввел вычислительную технику, теперь известную как спектральная последовательность Лере . Это дало связь между группами когомологий пучка и группами когомологий прямого образа пучка . Связь включала бесконечный процесс. Лере обнаружил, что группы когомологий прямого образа образуют естественный цепной комплекс , так что он мог взять когомологии когомологий. Это все еще не было когомологиями исходного пучка, но в некотором смысле это было на шаг ближе. Когомологии когомологий снова образовывали цепной комплекс, а его когомологии образовывали цепной комплекс и так далее. Предел этого бесконечного процесса был по существу таким же, как и у групп когомологий исходного пучка.

Вскоре стало ясно, что вычислительная техника Лере была примером более общего явления. Спектральные последовательности были обнаружены в различных ситуациях, и они давали сложные отношения между группами гомологии и когомологии, происходящими из геометрических ситуаций, таких как расслоения , и из алгебраических ситуаций, включающих производные функторы . Хотя их теоретическое значение уменьшилось с введением производных категорий , они по-прежнему являются наиболее эффективным доступным вычислительным инструментом. Это верно даже тогда, когда многие члены спектральной последовательности невычислимы.

К сожалению, из-за большого объема информации, переносимой в спектральных последовательностях, их трудно понять. Эта информация обычно содержится в решетке ранга три абелевых групп или модулей . Проще всего иметь дело с теми случаями, в которых спектральная последовательность в конечном итоге разрушается, что означает, что дальнейшее продвижение по последовательности не дает новой информации. Даже когда этого не происходит, часто можно получить полезную информацию из спектральной последовательности с помощью различных трюков.

Зафиксируем абелеву категорию , например категорию модулей над кольцом , и неотрицательное целое число . Когомологическая спектральная последовательность — это последовательность объектов и эндоморфизмов , такая, что для каждого${\displaystyle r_{0}}$${\displaystyle \{E_{r},d_{r}\}_{r\geq r_{0}}}$${\displaystyle E_{r}}$${\displaystyle d_{r}:E_{r}\to E_{r}}$${\displaystyle r\geq r_{0}}$

1. ${\displaystyle d_{r}\circ d_{r}=0}$,
2. ${\displaystyle E_{r+1}\cong H_{*}(E_{r},d_{r})}$, гомологии относительно .​${\displaystyle E_{r}}$${\displaystyle d_{r}}$

Обычно изоморфизмы подавляются, и вместо этого мы пишем. Объект называется листом (как в листе бумаги ), а иногда страницей или термином ; эндоморфизм называется граничной картой или дифференциалом . Иногда называется производным объектом . [ ^{требуется цитата ]}${\displaystyle E_{r+1}=H_{*}(E_{r},d_{r})}$${\displaystyle E_{r}}$${\displaystyle d_{r}}$${\displaystyle E_{r+1}}$${\displaystyle E_{r}}$

В действительности спектральные последовательности в основном встречаются в категории дважды градуированных модулей над кольцом R (или дважды градуированных пучков модулей над пучком колец), т.е. каждый лист является биградуированным R-модулем. Таким образом, в этом случае когомологическая спектральная последовательность является последовательностью биградуированных R-модулей и для каждого модуля прямой суммой эндоморфизмов бистепени , такой что для каждого выполняется следующее:${\textstyle E_{r}=\bigoplus _{p,q\in \mathbb {Z} ^{2}}E_{r}^{p,q}.}$${\displaystyle \{E_{r},d_{r}\}_{r\geq r_{0}}}$${\displaystyle \{E_{r}^{p,q}\}_{p,q}}$${\displaystyle d_{r}=(d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1})_{p,q\in \mathbb {Z} ^{2}}}$${\displaystyle (r,1-r)}$${\displaystyle r\geq r_{0}}$

1. ${\displaystyle d_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}=0}$,
2. ${\displaystyle E_{r+1}\cong H_{*}(E_{r},d_{r})}$.

Используемая здесь нотация называется дополнительной степенью . Некоторые авторы пишут вместо этого, где — общая степень . В зависимости от спектральной последовательности граничная карта на первом листе может иметь степень, которая соответствует r = 0, r = 1 или r = 2. Например, для спектральной последовательности отфильтрованного комплекса, описанной ниже, r ₀ = 0, но для спектральной последовательности Гротендика , r ₀ = 2. Обычно r ₀ равно нулю, единице или двум. В неградуированной ситуации, описанной выше, r ₀ не имеет значения.${\displaystyle E_{r}^{d,q}}$${\displaystyle d=p+q}$

Чаще всего речь идет о цепных комплексах , которые встречаются в порядке убывания (как выше) или возрастания. В последнем случае, заменив на и на (бистепень ), получаем определение гомологической спектральной последовательности аналогично когомологическому случаю.${\displaystyle E_{r}^{p,q}}$${\displaystyle E_{p,q}^{r}}$${\displaystyle d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1}}$${\displaystyle d_{p,q}^{r}:E_{p,q}^{r}\to E_{pr,q+r-1}^{r}}$${\displaystyle (-r,r-1)}$

Самым элементарным примером в неградуированной ситуации является цепной комплекс C _• . Объект C _• в абелевой категории цепных комплексов естественным образом имеет дифференциал d . Пусть r ₀ = 0, и пусть E ₀ будет C _• . Это заставляет E ₁ быть комплексом H ( C _• ): В i '-м положении это i '-я группа гомологии C _• . Единственный естественный дифференциал на этом новом комплексе — это нулевое отображение, поэтому мы положим d ₁ = 0. Это заставляет равняться , и снова наш единственный естественный дифференциал — это нулевое отображение. Помещение нулевого дифференциала на все остальные наши листы дает спектральную последовательность, члены которой:${\displaystyle E_{2}}$${\displaystyle E_{1}}$

• Э ₀ = С _•
• E _r = H ( C _• ) для всех r ≥ 1.

Члены этой спектральной последовательности стабилизируются на первом листе, поскольку ее единственный нетривиальный дифференциал был на нулевом листе. Следовательно, мы не можем получить больше информации на более поздних шагах. Обычно, чтобы получить полезную информацию с более поздних листов, нам нужна дополнительная структура на .${\displaystyle E_{r}}$

Спектральная последовательность с двойной градацией имеет огромный объем данных для отслеживания, но существует общая техника визуализации, которая делает структуру спектральной последовательности более ясной. У нас есть три индекса, r , p и q . Объект можно рассматривать как клетчатую страницу книги. На этих листах мы будем считать p горизонтальным направлением, а q вертикальным направлением. В каждой точке решетки у нас есть объект . Теперь переход к следующей странице означает принятие гомологии, то есть страница является подчастным страницы . Общая степень n = p + q проходит по диагонали, с северо-запада на юго-восток, через каждый лист. В гомологическом случае дифференциалы имеют бистепень (− r ,  r  − 1), поэтому они уменьшают n на единицу. В когомологическом случае n увеличивается на единицу. Дифференциалы меняют свое направление с каждым поворотом относительно r.${\displaystyle E_{r}}$${\displaystyle r^{th}}$${\displaystyle E_{r}^{p,q}}$${\displaystyle (r+1)^{th}}$${\displaystyle r^{th}}$

Красные стрелки демонстрируют случай последовательности первого квадранта (см. пример ниже), где только объекты первого квадранта ненулевые. При перелистывании страниц либо домен, либо кодомен всех дифференциалов становятся нулевыми.

Множество когомологических спектральных последовательностей образует категорию: морфизм спектральных последовательностей по определению является набором отображений , которые совместимы с дифференциалами, т.е. , и с заданными изоморфизмами между когомологиями r -го шага и (r+1) -ми листами E и E' , соответственно: . В биградуированном случае они также должны соблюдать градуировку:${\displaystyle f:E\to E'}$${\displaystyle f_{r}:E_{r}\to E'_{r}}$${\displaystyle f_{r}\circ d_{r}=d'_{r}\circ f_{r}}$${\displaystyle f_{r+1}(E_{r+1})\,=\,f_{r+1}(H(E_{r}))\,=\,H(f_{r}(E_{r}))}$${\displaystyle f_{r}(E_{r}^{p,q})\subset {E'_{r}}^{p,q}.}$

Произведение чашек дает кольцевую структуру группе когомологий, превращая ее в когомологическое кольцо . Таким образом, естественно рассмотреть спектральную последовательность с кольцевой структурой. Пусть будет спектральной последовательностью когомологического типа. Мы говорим, что она имеет мультипликативную структуру, если (i) являются (дважды градуированными) дифференциально-градуированными алгебрами и (ii) умножение на индуцируется умножением на через переход к когомологиям.${\displaystyle E_{r}^{p,q}}$${\displaystyle E_{r}}$${\displaystyle E_{r+1}}$${\displaystyle E_{r}}$

Типичным примером является когомологическая спектральная последовательность Серра для расслоения , когда группа коэффициентов является кольцом R. Она имеет мультипликативную структуру, индуцированную произведениями чашек волокна и базы на -странице. ^[1] Однако, в общем случае предельный член не изоморфен как градуированная алгебра H( E ; R ). ^[2] Мультипликативная структура может быть очень полезна для вычисления дифференциалов на последовательности. ^[3]${\displaystyle F\to E\to B}$${\displaystyle E_{2}}$${\displaystyle E_{\infty}}$

Спектральные последовательности могут быть построены различными способами. В алгебраической топологии точная пара, пожалуй, является наиболее распространенным инструментом для построения. В алгебраической геометрии спектральные последовательности обычно строятся из фильтраций коцепных комплексов.

Другой метод построения спектральных последовательностей — метод точных пар Уильяма Мэсси . Точные пары особенно распространены в алгебраической топологии. Несмотря на это, они непопулярны в абстрактной алгебре, где большинство спектральных последовательностей получаются из отфильтрованных комплексов.

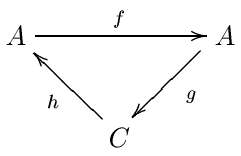
Чтобы определить точные пары, мы снова начнем с абелевой категории. Как и прежде, на практике это обычно категория дважды градуированных модулей над кольцом. Точная пара — это пара объектов ( A , C ), вместе с тремя гомоморфизмами между этими объектами: f  : A → A , g  : A → C и h  : C → A, подчиненные определенным условиям точности:

• Изображение f = Ядро g
• Изображение g = Ядро h
• Изображение h = Ядро f

Мы будем сокращать эти данные как ( A , C , f , g , h ). Точные пары обычно изображаются в виде треугольников. Мы увидим, что _C соответствует члену E0 спектральной последовательности, а A — это некоторые вспомогательные данные.

Для перехода к следующему листу спектральной последовательности сформируем производную пару . Зададим:

• д = г о ч
• А' = ф ( А )
• C' = Кер д / Им д
• f ' = f | _A' , ограничение f на A'
• h'  : C' → A' индуцируется h . Легко видеть, что h индуцирует такое отображение.
• g'  : A' → C' определяется на элементах следующим образом: для каждого a в A' запишем a как f ( b ) для некоторого b в A . g' ( a ) определяется как образ g ( b ) в C' . В общем случае g' можно построить с помощью одной из теорем вложения для абелевых категорий.

Отсюда легко проверить, что ( A' , C' , f' , g' , h' ) — точная пара. C' соответствует члену E ₁ спектральной последовательности. Мы можем повторить эту процедуру, чтобы получить точные пары ( A ^{( n )} , C ^{( n )} , f ^{( n )} , g ^{( n )} , h ^{( n )} ).

Чтобы построить спектральную последовательность, пусть E _n будет C ^{( n )} и d _n будет g ^{( n )} o h ^{( n )} .

• Спектральная последовательность Серра ^[4] - используется для вычисления (ко)гомологий расслоения
• Спектральная последовательность Атьи–Хирцебруха — используется для вычисления (ко)гомологий необычных теорий когомологий, таких как K-теория.
• Спектральная последовательность Бокштейна .
• Спектральные последовательности отфильтрованных комплексов

Очень распространенный тип спектральной последовательности происходит из отфильтрованного коцепного комплекса, поскольку он естественным образом индуцирует биградуированный объект. Рассмотрим коцепной комплекс вместе с нисходящей фильтрацией, . Мы требуем, чтобы граничное отображение было совместимо с фильтрацией, т. е . , и чтобы фильтрация была исчерпывающей , то есть объединение множества всех является всем цепным комплексом . Тогда существует спектральная последовательность с и . ^[5] Позже мы также предположим, что фильтрация является хаусдорфовой или разделенной , то есть пересечение множества всех равно нулю.${\displaystyle (C^{\bullet },d)}$${\textstyle ...\supset \,F^{-2}C^{\bullet }\,\supset \,F^{-1}C^{\bullet }\supset F^{0}C^{\bullet }\,\supset \,F^{1}C^{\bullet }\,\supset \,F^{2}C^{\bullet }\,\supset \,F^{3}C^{\bullet }\,\supset ...\,}$${\textstyle d(F^{p}C^{n})\subset F^{p}C^{n+1}}$${\textstyle F^{p}C^{\bullet }}$${\textstyle C^{\bullet }}$${\textstyle E_{0}^{p,q}=F^{p}C^{p+q}/F^{p+1}C^{p+q}}$${\textstyle E_{1}^{p,q}=H^{p+q}(F^{p}C^{\bullet }/F^{p+1}C^{\bullet })}$${\textstyle F^{p}C^{\bullet }}$

Фильтрация полезна, поскольку она дает меру близости к нулю: по мере увеличения p становится все ближе и ближе к нулю. Мы построим спектральную последовательность из этой фильтрации, где кограницы и коциклы в более поздних листах становятся все ближе и ближе к кограницам и коциклам в исходном комплексе. Эта спектральная последовательность дважды градуируется степенью фильтрации p и дополнительной степенью q = n − p .${\textstyle F^{p}C^{\bullet }}$

${\displaystyle C^{\bullet }}$имеет только одну градацию и фильтрацию, поэтому сначала мы строим дважды градуированный объект для первой страницы спектральной последовательности. Чтобы получить вторую градацию, мы возьмем связанный градуированный объект относительно фильтрации. Мы запишем его необычным способом, который будет обоснован на шаге :${\displaystyle E_{1}}$

${\displaystyle Z_{-1}^{p,q}=Z_{0}^{p,q}=F^{p}C^{p+q}}$

${\displaystyle B_{0}^{p,q}=0}$

${\displaystyle E_{0}^{p,q}={\frac {Z_{0}^{p,q}}{B_{0}^{p,q}+Z_{-1}^{p+1,q-1}}}={\frac {F^{p}C^{p+q}}{F^{p+1}C^{p+q}}}}$

${\displaystyle E_{0}=\bigoplus _{p,q\in \mathbf {Z} }E_{0}^{p,q}}$

Поскольку мы предположили, что граничная карта совместима с фильтрацией, является дважды градуированным объектом и существует естественная дважды градуированная граничная карта на . Чтобы получить , мы берем гомологию .${\displaystyle E_{0}}$${\displaystyle d_{0}}$${\displaystyle E_{0}}$${\displaystyle E_{1}}$${\displaystyle E_{0}}$

${\displaystyle {\bar {Z}}_{1}^{p,q}=\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}=\ker d_{0}^{p,q}:F^{p}C^{p+q}/F^{p+1}C^{p+q}\rightarrow F^{p}C^{p+q+1}/F^{p+1}C^{p+q+1}}$

${\displaystyle {\bar {B}}_{1}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}/F^{p+1}C^{p+q-1}\rightarrow F^{p}C^{p+q}/F^{p+1}C^{p+q}}$

${\displaystyle E_{1}^{p,q}={\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}={\frac {\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}}{{\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}}}}$

${\displaystyle E_{1}=\bigoplus _{p,q\in \mathbf {Z} }E_{1}^{p,q}=\bigoplus _{p,q\in \mathbf {Z} }{\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}}$

Обратите внимание, что и можно записать как изображения в${\displaystyle {\bar {Z}}_{1}^{p,q}}$${\displaystyle {\bar {B}}_{1}^{p,q}}$${\displaystyle E_{0}^{p,q}}$

${\displaystyle Z_{1}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+1}C^{p+q+1}}$

${\displaystyle B_{1}^{p,q}=({\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$

и что мы тогда имеем

${\displaystyle E_{1}^{p,q}={\frac {Z_{1}^{p,q}}{B_{1}^{p,q}+Z_{0}^{p+1,q-1}}}.}$

${\displaystyle Z_{1}^{p,q}}$являются именно теми элементами, которые дифференциал поднимает на один уровень в фильтрации, и являются именно теми элементами, которые дифференциал поднимает на нулевые уровни в фильтрации. Это предполагает, что мы должны выбрать быть элементами, которые дифференциал поднимает на r уровней в фильтрации, и быть образом элементов, которые дифференциал поднимает на r-1 уровней в фильтрации. Другими словами, спектральная последовательность должна удовлетворять${\displaystyle B_{1}^{p,q}}$${\displaystyle Z_{r}^{p,q}}$${\displaystyle B_{r}^{p,q}}$

${\displaystyle Z_{r}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1}}$

${\displaystyle B_{r}^{p,q}=({\mbox{im }}d_{0}^{p-r+1,q+r-2}:F^{p-r+1}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$

${\displaystyle E_{r}^{p,q}={\frac {Z_{r}^{p,q}}{B_{r}^{p,q}+Z_{r-1}^{p+1,q-1}}}}$

и у нас должны быть отношения

${\displaystyle B_{r}^{p,q}=d_{0}^{p,q}(Z_{r-1}^{p-r+1,q+r-2}).}$

Чтобы это имело смысл, мы должны найти дифференциал на каждом и проверить, что он приводит к гомологии, изоморфной . Дифференциал ${\displaystyle d_{r}}$${\displaystyle E_{r}}$${\displaystyle E_{r+1}}$

${\displaystyle d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}}$

определяется ограничением исходного дифференциала, определенного на подобъекте . Легко проверить, что гомология относительно этого дифференциала равна , поэтому это дает спектральную последовательность. К сожалению, дифференциал не очень явный. Определение дифференциалов или поиск способов их обойти — одна из главных проблем успешного применения спектральной последовательности.${\displaystyle d}$${\displaystyle C^{p+q}}$${\displaystyle Z_{r}^{p,q}}$${\displaystyle E_{r}}$${\displaystyle E_{r+1}}$

• Спектральная последовательность Ходжа-де Рама
• Спектральная последовательность двойного комплекса
• Может использоваться для создания смешанных структур Ходжа ^[6]

Другая распространенная спектральная последовательность — это спектральная последовательность двойного комплекса. Двойной комплекс — это набор объектов C _i,j для всех целых чисел i и j вместе с двумя дифференциалами, d ^I и d ^II . Предполагается, что d ^I уменьшает i , а d ^II уменьшает j . Кроме того, мы предполагаем, что дифференциалы антикоммутируют , так что d ^I d ^II + d ^II d ^I = 0. Наша цель — сравнить итерированные гомологии и . Мы сделаем это, отфильтровав наш двойной комплекс двумя разными способами. Вот наши фильтрации:${\displaystyle H_{i}^{I}(H_{j}^{II}(C_{\bullet ,\bullet }))}$${\displaystyle H_{j}^{II}(H_{i}^{I}(C_{\bullet ,\bullet }))}$

${\displaystyle (C_{i,j}^{I})_{p}={\begin{cases}0&{\text{if }}i<p\\C_{i,j}&{\text{if }}i\geq p\end{cases}}}$

${\displaystyle (C_{i,j}^{II})_{p}={\begin{cases}0&{\text{if }}j<p\\C_{i,j}&{\text{if }}j\geq p\end{cases}}}$

Чтобы получить спектральную последовательность, мы сведем ее к предыдущему примеру. Мы определяем полный комплекс T ( C _•,• ) как комплекс, n -й член которого равен и дифференциал которого равен d ^I + d ^II . Это комплекс, потому что d ^I и d ^II являются антикоммутирующими дифференциалами. Две фильтрации на C _i,j дают две фильтрации на полном комплексе:${\displaystyle \bigoplus _{i+j=n}C_{i,j}}$

${\displaystyle T_{n}(C_{\bullet ,\bullet })_{p}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}}$

${\displaystyle T_{n}(C_{\bullet ,\bullet })_{p}^{II}=\bigoplus _{i+j=n \atop j>p-1}C_{i,j}}$

Чтобы показать, что эти спектральные последовательности дают информацию об итерированных гомологиях, мы вычислим члены E ⁰ , E ¹ и E ² фильтрации I на T ( C _•,• ). Член E ⁰ ясен:

${\displaystyle {}^{I}E_{p,q}^{0}=T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}{\Big /}\bigoplus _{i+j=n \atop i>p}C_{i,j}=C_{p,q},}$

где n = p + q .

Чтобы найти член E ¹ , нам нужно определить d ^I + d ^II на E ⁰ . Обратите внимание, что дифференциал должен иметь степень −1 относительно n , поэтому мы получаем отображение

${\displaystyle d_{p,q}^{I}+d_{p,q}^{II}:T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q}\rightarrow T_{n-1}(C_{\bullet ,\bullet })_{p}^{I}/T_{n-1}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q-1}}$

Следовательно, дифференциал на E ⁰ — это отображение C _{p , q} → C _{p , q −1,} индуцированное d ^I + d ^II . Но d ^I имеет неправильную степень, чтобы индуцировать такое отображение, поэтому d ^I должно быть равно нулю на E ⁰ . Это означает, что дифференциал — это в точности d ^II , поэтому мы получаем

${\displaystyle {}^{I}E_{p,q}^{1}=H_{q}^{II}(C_{p,\bullet }).}$

Чтобы найти E ² , нам нужно определить

${\displaystyle d_{p,q}^{I}+d_{p,q}^{II}:H_{q}^{II}(C_{p,\bullet })\rightarrow H_{q}^{II}(C_{p+1,\bullet })}$

Поскольку E ¹ был в точности гомологией относительно d ^II , d ^II равен нулю на E ^1. Следовательно, мы получаем

${\displaystyle {}^{I}E_{p,q}^{2}=H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet })).}$

Использование другой фильтрации дает нам другую спектральную последовательность с похожим ^членом E2 :

${\displaystyle {}^{II}E_{p,q}^{2}=H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet })).}$

Остается найти связь между этими двумя спектральными последовательностями. Окажется, что по мере увеличения r обе последовательности станут достаточно похожими, чтобы позволить полезные сравнения.

Пусть E _r — спектральная последовательность, начинающаяся, скажем, с r = 1. Тогда существует последовательность подобъектов

${\displaystyle 0=B_{0}\subset B_{1}\subset B_{2}\subset \dots \subset B_{r}\subset \dots \subset Z_{r}\subset \dots \subset Z_{2}\subset Z_{1}\subset Z_{0}=E_{1}}$

такой что ; действительно, рекурсивно мы позволяем и позволяем быть так, что являются ядром и образом${\displaystyle E_{r}\simeq Z_{r-1}/B_{r-1}}$${\displaystyle Z_{0}=E_{1},B_{0}=0}$${\displaystyle Z_{r},B_{r}}$${\displaystyle Z_{r}/B_{r-1},B_{r}/B_{r-1}}$${\displaystyle E_{r}{\overset {d_{r}}{\to }}E_{r}.}$

Затем мы позволяем и${\displaystyle Z_{\infty }=\cap _{r}Z_{r},B_{\infty }=\cup _{r}B_{r}}$

${\displaystyle E_{\infty }=Z_{\infty }/B_{\infty }}$;

он называется предельным членом . (Конечно, такой член не обязательно должен существовать в категории, но это обычно не является проблемой, поскольку, например, в категории модулей такие пределы существуют или поскольку на практике спектральная последовательность, с которой мы работаем, имеет тенденцию к вырождению; в последовательности выше имеется лишь конечное число включений.)${\displaystyle E_{\infty }}$

Мы говорим, что спектральная последовательность сходится слабо, если существует градуированный объект с фильтрацией для каждого , и для каждого существует изоморфизм . Она сходится к , если фильтрация является хаусдорфовой, т.е. . Мы пишем${\displaystyle H^{\bullet }}$${\displaystyle F^{\bullet }H^{n}}$${\displaystyle n}$${\displaystyle p}$${\displaystyle E_{\infty }^{p,q}\cong F^{p}H^{p+q}/F^{p+1}H^{p+q}}$${\displaystyle H^{\bullet }}$${\displaystyle F^{\bullet }H^{n}}$${\displaystyle \cap _{p}F^{p}H^{\bullet }=0}$

${\displaystyle E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{n}}$

означает, что всякий раз, когда p + q = n , сходится к . Мы говорим, что спектральная последовательность примыкает к , если для каждого существует такое, что для всех , . Тогда — предельный член. Спектральная последовательность регулярна или вырождается при , если дифференциалы равны нулю для всех . Если, в частности, существует , такое, что лист сосредоточен на одной строке или одном столбце, то мы говорим, что он схлопывается . В символах мы пишем:${\displaystyle E_{r}^{p,q}}$${\displaystyle E_{\infty }^{p,q}}$${\displaystyle E_{r}^{p,q}}$ ${\displaystyle E_{\infty }^{p,q}}$${\displaystyle p,q}$${\displaystyle r(p,q)}$${\displaystyle r\geq r(p,q)}$${\displaystyle E_{r}^{p,q}=E_{r(p,q)}^{p,q}}$${\displaystyle E_{r(p,q)}^{p,q}=E_{\infty }^{p,q}}$${\displaystyle r_{0}}$ ${\displaystyle d_{r}^{p,q}}$${\displaystyle r\geq r_{0}}$${\displaystyle r_{0}\geq 2}$${\displaystyle r_{0}^{th}}$

${\displaystyle E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{p,q}}$

P указывает индекс фильтрации. Очень часто термин пишут слева от опоры, потому что это самый полезный термин большинства спектральных последовательностей. Спектральная последовательность нефильтрованного цепного комплекса вырождается на первом листе (см. первый пример): поскольку после нулевого листа ничего не происходит, предельный лист совпадает с .${\displaystyle E_{2}^{p,q}}$${\displaystyle E_{\infty }}$${\displaystyle E_{1}}$

Пятичленная точная последовательность спектральной последовательности связывает определенные члены низкой степени и _члены E∞ .

Обратите внимание, что у нас есть цепочка включений:

${\displaystyle Z_{0}^{p,q}\supseteq Z_{1}^{p,q}\supseteq Z_{2}^{p,q}\supseteq \cdots \supseteq B_{2}^{p,q}\supseteq B_{1}^{p,q}\supseteq B_{0}^{p,q}}$

Мы можем спросить, что произойдет, если мы определим

${\displaystyle Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q},}$

${\displaystyle B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q},}$

${\displaystyle E_{\infty }^{p,q}={\frac {Z_{\infty }^{p,q}}{B_{\infty }^{p,q}+Z_{\infty }^{p+1,q-1}}}.}$

${\displaystyle E_{\infty }^{p,q}}$является естественным кандидатом на опору этой спектральной последовательности. Сходимость не является автоматической, но происходит во многих случаях. В частности, если фильтрация конечна и состоит ровно из r нетривиальных шагов, то спектральная последовательность вырождается после r -го листа. Сходимость также происходит, если комплекс и фильтрация оба ограничены снизу или оба ограничены сверху.

Чтобы более подробно описать основу нашей спектральной последовательности, обратите внимание, что у нас есть формулы:

${\displaystyle Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q}=\bigcap _{r=0}^{\infty }\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1})}$

${\displaystyle B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q}=\bigcup _{r=0}^{\infty }({\mbox{im }}d^{p,q-r}:F^{p-r}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$

Чтобы увидеть, что это означает для напомним, что мы предположили, что фильтрация была разделена. Это подразумевает, что по мере увеличения r ядра уменьшаются, пока не останется . Для напомним, что мы предположили, что фильтрация была исчерпывающей. Это подразумевает, что по мере увеличения r изображения растут, пока мы не достигнем . Мы заключаем${\displaystyle Z_{\infty }^{p,q}}$${\displaystyle Z_{\infty }^{p,q}=\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1})}$${\displaystyle B_{\infty }^{p,q}}$${\displaystyle B_{\infty }^{p,q}={\text{im }}(C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}$

${\displaystyle E_{\infty }^{p,q}={\mbox{gr}}_{p}H^{p+q}(C^{\bullet })}$,

то есть, опора спектральной последовательности является p- й градуированной частью (p+q) -й гомологии C. Если наша спектральная последовательность сходится, то мы заключаем, что:

${\displaystyle E_{r}^{p,q}\Rightarrow _{p}H^{p+q}(C^{\bullet })}$

Используя спектральную последовательность отфильтрованного комплекса, мы можем вывести существование длинных точных последовательностей . Выберем короткую точную последовательность коцепных комплексов 0 → A ^• → B ^• → C ^• → 0 и назовем первое отображение f ^•  : A ^• → B ^• . Мы получаем естественные отображения объектов гомологии H ⁿ ( A ^• ) → H ⁿ ( B ^• ) → H ⁿ ( C ^• ), и мы знаем, что это точно в середине. Мы будем использовать спектральную последовательность отфильтрованного комплекса, чтобы найти связывающий гомоморфизм и доказать, что полученная последовательность точна. Для начала мы отфильтруем B ^• :

${\displaystyle F^{0}B^{n}=B^{n}}$

${\displaystyle F^{1}B^{n}=A^{n}}$

${\displaystyle F^{2}B^{n}=0}$

Это дает:

${\displaystyle E_{0}^{p,q}={\frac {F^{p}B^{p+q}}{F^{p+1}B^{p+q}}}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\C^{q}&{\text{if }}p=0\\A^{q+1}&{\text{if }}p=1\end{cases}}}$

${\displaystyle E_{1}^{p,q}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(C^{\bullet })&{\text{if }}p=0\\H^{q+1}(A^{\bullet })&{\text{if }}p=1\end{cases}}}$

Дифференциал имеет бистепень (1, 0), поэтому d _0,q  : H ^q ( C ^• ) → H ^{q +1} ( A ^• ). Это связующие гомоморфизмы из леммы о змее , и вместе с отображениями A ^• → B ^• → C ^• они дают последовательность:

${\displaystyle \cdots \rightarrow H^{q}(B^{\bullet })\rightarrow H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\rightarrow \cdots }$

Осталось показать, что эта последовательность точна в точках A и C. Обратите внимание, что эта спектральная последовательность вырождается в члене E ₂ , поскольку дифференциалы имеют бистепень (2, −1). Следовательно, член E ₂ совпадает с членом E _∞ :

${\displaystyle E_{2}^{p,q}\cong {\text{gr}}_{p}H^{p+q}(B^{\bullet })={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(B^{\bullet })/H^{q}(A^{\bullet })&{\text{if }}p=0\\{\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })&{\text{if }}p=1\end{cases}}}$

Но у нас также есть прямое описание термина E ₂ как гомологии термина E _1. Эти два описания должны быть изоморфны:

${\displaystyle H^{q}(B^{\bullet })/H^{q}(A^{\bullet })\cong \ker d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })}$

${\displaystyle {\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\cong H^{q+1}(A^{\bullet })/({\mbox{im }}d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet }))}$

Первый вариант обеспечивает точность в точке C , а второй вариант обеспечивает точность в точке A.

Используя опору для отфильтрованного комплекса, мы обнаруживаем, что:

${\displaystyle H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet }))\Rightarrow _{p}H^{p+q}(T(C_{\bullet ,\bullet }))}$

${\displaystyle H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet }))\Rightarrow _{q}H^{p+q}(T(C_{\bullet ,\bullet }))}$

В общем случае две градации на H ^p+q (T(C _•,• )) различны . Несмотря на это, все еще возможно получить полезную информацию из этих двух спектральных последовательностей.

Пусть R — кольцо, M — правый R -модуль, а N — левый R -модуль. Напомним, что производные функторы тензорного произведения обозначаются Tor . Tor определяется с помощью проективного разрешения своего первого аргумента. Однако оказывается, что . Хотя это можно проверить без спектральной последовательности, со спектральными последовательностями это сделать очень просто.${\displaystyle \operatorname {Tor} _{i}(M,N)=\operatorname {Tor} _{i}(N,M)}$

Выберите проективные разрешения и M и N , соответственно. Рассмотрим их как комплексы, которые исчезают в отрицательной степени, имеющие дифференциалы d и e , соответственно. Мы можем построить двойной комплекс, члены которого и дифференциалы которого и . (Множитель −1 таков, что дифференциалы антикоммутируют.) Поскольку проективные модули плоские, взятие тензорного произведения с проективным модулем коммутирует с взятием гомологии, поэтому мы получаем:${\displaystyle P_{\bullet }}$${\displaystyle Q_{\bullet }}$${\displaystyle C_{i,j}=P_{i}\otimes Q_{j}}$${\displaystyle d\otimes 1}$${\displaystyle (-1)^{i}(1\otimes e)}$

${\displaystyle H_{p}^{I}(H_{q}^{II}(P_{\bullet }\otimes Q_{\bullet }))=H_{p}^{I}(P_{\bullet }\otimes H_{q}^{II}(Q_{\bullet }))}$

${\displaystyle H_{q}^{II}(H_{p}^{I}(P_{\bullet }\otimes Q_{\bullet }))=H_{q}^{II}(H_{p}^{I}(P_{\bullet })\otimes Q_{\bullet })}$

Поскольку два комплекса являются разрешениями, их гомология исчезает вне нулевой степени. В нулевой степени мы остаемся с

${\displaystyle H_{p}^{I}(P_{\bullet }\otimes N)=\operatorname {Tor} _{p}(M,N)}$

${\displaystyle H_{q}^{II}(M\otimes Q_{\bullet })=\operatorname {Tor} _{q}(N,M)}$

В частности, члены исчезают, за исключением линий q = 0 (для спектральной последовательности I ) и p = 0 (для спектральной последовательности II ). Это означает, что спектральная последовательность вырождается на втором листе, поэтому члены E ^∞ изоморфны членам E ² :${\displaystyle E_{p,q}^{2}}$

${\displaystyle \operatorname {Tor} _{p}(M,N)\cong E_{p}^{\infty }=H_{p}(T(C_{\bullet ,\bullet }))}$

${\displaystyle \operatorname {Tor} _{q}(N,M)\cong E_{q}^{\infty }=H_{q}(T(C_{\bullet ,\bullet }))}$

Наконец, когда p и q равны, обе правые части равны, и отсюда следует коммутативность Tor.

Рассмотрим спектральную последовательность, где обращается в нуль для всех меньших, чем некоторые и для всех меньших, чем некоторые . Если и можно выбрать равными нулю, это называется спектральной последовательностью первого квадранта . Последовательность примыкает, поскольку выполняется для всех , если и . Чтобы увидеть это, обратите внимание, что либо область, либо кодомен дифференциала равны нулю для рассматриваемых случаев. Визуально листы стабилизируются в растущем прямоугольнике (см. рисунок выше). Однако спектральная последовательность не обязательно должна вырождаться, поскольку дифференциальные отображения могут не все быть нулевыми одновременно. Аналогично спектральная последовательность также сходится, если обращается в нуль для всех больших, чем некоторые и для всех больших, чем некоторые .${\displaystyle E_{r}^{p,q}}$${\displaystyle p}$${\displaystyle p_{0}}$${\displaystyle q}$${\displaystyle q_{0}}$${\displaystyle p_{0}}$${\displaystyle q_{0}}$${\displaystyle E_{r+i}^{p,q}=E_{r}^{p,q}}$${\displaystyle i\geq 0}$${\displaystyle r>p}$${\displaystyle r>q+1}$${\displaystyle E_{r}^{p,q}}$${\displaystyle p}$${\displaystyle p_{0}}$${\displaystyle q}$${\displaystyle q_{0}}$

Пусть будет гомологической спектральной последовательностью такой, что для всех p, отличных от 0, 1. Визуально это спектральная последовательность с -страницей${\displaystyle E_{p,q}^{r}}$${\displaystyle E_{p,q}^{2}=0}$${\displaystyle E^{2}}$

${\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&E_{1,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&E_{1,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&E_{1,0}^{2}&0&\cdots \\\cdots &0&E_{0,-1}^{2}&E_{1,-1}^{2}&0&\cdots \\&\vdots &\vdots &\vdots &\vdots &\end{matrix}}}$

Дифференциалы на второй странице имеют степень (-2, 1), поэтому они имеют вид

${\displaystyle d_{p,q}^{2}:E_{p,q}^{2}\to E_{p-2,q+1}^{2}}$

Все эти карты равны нулю, так как они

${\displaystyle d_{0,q}^{2}:E_{0,q}^{2}\to 0}$,${\displaystyle d_{1,q}^{2}:E_{1,q}^{2}\to 0}$

следовательно, спектральная последовательность вырождается: . Скажем, она сходится к с фильтрацией${\displaystyle E^{\infty }=E^{2}}$${\displaystyle H_{*}}$

${\displaystyle 0=F_{-1}H_{n}\subset F_{0}H_{n}\subset \dots \subset F_{n}H_{n}=H_{n}}$

такой, что . Тогда , , , , и т.д. Таким образом, имеет место точная последовательность: ^[7]${\displaystyle E_{p,q}^{\infty }=F_{p}H_{p+q}/F_{p-1}H_{p+q}}$${\displaystyle F_{0}H_{n}=E_{0,n}^{2}}$${\displaystyle F_{1}H_{n}/F_{0}H_{n}=E_{1,n-1}^{2}}$${\displaystyle F_{2}H_{n}/F_{1}H_{n}=0}$${\displaystyle F_{3}H_{n}/F_{2}H_{n}=0}$

${\displaystyle 0\to E_{0,n}^{2}\to H_{n}\to E_{1,n-1}^{2}\to 0}$.

Далее, пусть будет спектральной последовательностью, вторая страница которой состоит только из двух строк q = 0, 1. Это не обязательно вырождается на второй странице, но все равно вырождается на третьей странице, поскольку дифференциалы там имеют степень (-3, 2). Обратите внимание , так как знаменатель равен нулю. Аналогично, . Таким образом,${\displaystyle E_{p,q}^{r}}$${\displaystyle E_{p,0}^{3}=\operatorname {ker} (d:E_{p,0}^{2}\to E_{p-2,1}^{2})}$${\displaystyle E_{p,1}^{3}=\operatorname {coker} (d:E_{p+2,0}^{2}\to E_{p,1}^{2})}$

${\displaystyle 0\to E_{p,0}^{\infty }\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to E_{p-2,1}^{\infty }\to 0}$.

Теперь, скажем, спектральная последовательность сходится к H с фильтрацией F , как в предыдущем примере. Поскольку , , и т.д., то имеем: . Собирая все вместе, получаем: ^[8]${\displaystyle F_{p-2}H_{p}/F_{p-3}H_{p}=E_{p-2,2}^{\infty }=0}$${\displaystyle F_{p-3}H_{p}/F_{p-4}H_{p}=0}$${\displaystyle 0\to E_{p-1,1}^{\infty }\to H_{p}\to E_{p,0}^{\infty }\to 0}$

${\displaystyle \cdots \to H_{p+1}\to E_{p+1,0}^{2}{\overset {d}{\to }}E_{p-1,1}^{2}\to H_{p}\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to H_{p-1}\to \dots .}$

Вычисление в предыдущем разделе обобщается простым способом. Рассмотрим расслоение над сферой:

${\displaystyle F{\overset {i}{\to }}E{\overset {p}{\to }}S^{n}}$

при n не менее 2. Существует спектральная последовательность Серра :

${\displaystyle E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))\Rightarrow H_{p+q}(E)}$;

то есть с некоторой фильтрацией .${\displaystyle E_{p,q}^{\infty }=F_{p}H_{p+q}(E)/F_{p-1}H_{p+q}(E)}$${\displaystyle F_{\bullet }}$

Так как не равен нулю только тогда, когда p равен нулю или n и равен Z в этом случае, мы видим, что состоит только из двух строк , следовательно, -страница задается как${\displaystyle H_{p}(S^{n})}$${\displaystyle E_{p,q}^{2}}$${\displaystyle p=0,n}$${\displaystyle E^{2}}$

${\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&0&\cdots &0&E_{n,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&0&\cdots &0&E_{n,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&0&\cdots &0&E_{n,0}^{2}&0&\cdots \\\end{matrix}}}$

Более того, поскольку

${\displaystyle E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))=H_{q}(F)}$

по теореме об универсальном коэффициенте страница выглядит так${\displaystyle p=0,n}$${\displaystyle E^{2}}$