Точная последовательность

Точная последовательность — это последовательность морфизмов между объектами (например, группами , кольцами , модулями и, в более общем смысле, объектами абелевой категории ) такая, что образ одного морфизма равен ядру следующего.
Определение
В контексте теории групп последовательность
групп и групповых гомоморфизмов называется точной в , если . Последовательность называется точной , если она точна в каждом для всех , т. е. если образ каждого гомоморфизма равен ядру следующего.
Последовательность групп и гомоморфизмов может быть как конечной, так и бесконечной.
Аналогичное определение можно дать и для других алгебраических структур . Например, можно иметь точную последовательность векторных пространств и линейных отображений , или модулей и модульных гомоморфизмов . В более общем смысле, понятие точной последовательности имеет смысл в любой категории с ядрами и коядрами , и, в частности, в абелевых категориях , где оно широко используется.
Простые случаи
Чтобы понять определение, полезно рассмотреть относительно простые случаи, когда последовательность состоит из групповых гомоморфизмов, конечна и начинается или заканчивается тривиальной группой . Традиционно это, вместе с единственным элементом тождества, обозначается 0 (аддитивная нотация, обычно когда группы абелевы) или обозначается 1 (мультипликативная нотация).
- Рассмотрим последовательность 0 → A → B. Образ самого левого отображения равен 0. Поэтому последовательность точна тогда и только тогда, когда самое правое отображение (из A в B ) имеет ядро {0}; то есть тогда и только тогда, когда это отображение является мономорфизмом ( инъективным или взаимно-однозначным).
- Рассмотрим двойственную последовательность B → C → 0. Ядро самого правого отображения — это C. Поэтому последовательность точна тогда и только тогда, когда образ самого левого отображения (из B в C ) полностью совпадает с C ; то есть тогда и только тогда, когда это отображение является эпиморфизмом ( сюръективным или на).
- Следовательно, последовательность 0 → X → Y → 0 является точной тогда и только тогда, когда отображение из X в Y является как мономорфизмом, так и эпиморфизмом (то есть биморфизмом ), и поэтому обычно является изоморфизмом из X в Y (это всегда выполняется в точных категориях, таких как Set ).
Короткая точная последовательность
Короткие точные последовательности — это точные последовательности вида
Как установлено выше, для любой такой короткой точной последовательности f является мономорфизмом, а g является эпиморфизмом. Более того, образ f равен ядру g . Полезно думать об A как о подобъекте B с f, вставляющим A в B , и о C как о соответствующем факторном объекте (или факторе ), B / A , с g, индуцирующим изоморфизм
Короткая точная последовательность
называется расщепленным, если существует гомоморфизм h : C → B такой, что композиция g ∘ h является тождественным отображением на C. Отсюда следует, что если это абелевы группы , B изоморфна прямой сумме A и C :
Длинная точная последовательность
Общую точную последовательность иногда называют длинной точной последовательностью , чтобы отличить ее от частного случая короткой точной последовательности. [1]
Длинная точная последовательность эквивалентна семейству коротких точных последовательностей в следующем смысле: если задана длинная последовательность
(1)
при n ≥ 2 мы можем разбить его на короткие последовательности
(2)
где для каждого . По построению последовательности (2) точны в 's (независимо от точности (1) ). Более того, (1) является длинной точной последовательностью тогда и только тогда, когда (2) являются короткими точными последовательностями.
Подробную информацию о том, как переформировать длинную точную последовательность из коротких точных последовательностей, см. в лемме о плетении.
Примеры
Целые числа по модулю два
Рассмотрим следующую последовательность абелевых групп:
Первый гомоморфизм отображает каждый элемент i в множестве целых чисел Z в элемент 2 i в Z . Второй гомоморфизм отображает каждый элемент i в Z в элемент j в факторгруппе; то есть j = i mod 2 . Здесь стрелка-крючок указывает, что отображение 2× из Z в Z является мономорфизмом, а двунаправленная стрелка указывает на эпиморфизм (отображение mod 2). Это точная последовательность, поскольку изображение 2 Z мономорфизма является ядром эпиморфизма. По сути, «ту же самую» последовательность можно также записать как
В этом случае мономорфизм — это 2 n ↦ 2 n , и хотя он выглядит как тождественная функция, он не является онто (то есть не является эпиморфизмом), поскольку нечетные числа не принадлежат 2 Z . Однако образ 2 Z посредством этого мономорфизма — это точно то же самое подмножество Z , что и образ Z посредством n ↦ 2 n , использованный в предыдущей последовательности. Эта последняя последовательность отличается от предыдущей конкретной природой своего первого объекта, поскольку 2 Z — это не то же самое множество, что и Z , хотя они изоморфны как группы.
Первую последовательность можно также записать без использования специальных символов для мономорфизма и эпиморфизма:
Здесь 0 обозначает тривиальную группу, отображение из Z в Z является умножением на 2, а отображение из Z в фактор-группу Z /2 Z задается путем сокращения целых чисел по модулю 2. Это действительно точная последовательность:
- Образ отображения 0 → Z равен {0}, а ядро умножения на 2 также равно {0}, поэтому последовательность точна в первой точке Z.
- Образ умножения на 2 равен 2 Z , а ядро приведения по модулю 2 также равно 2 Z , поэтому последовательность точна во втором Z .
- Образ приведения по модулю 2 равен Z /2 Z , а ядро нулевого отображения также равно Z /2 Z , поэтому последовательность точна в позиции Z /2 Z .
Первая и третья последовательности являются своего рода особым случаем из-за бесконечной природы Z. Невозможно, чтобы конечная группа отображалась включением (то есть мономорфизмом) как собственная подгруппа самой себя. Вместо этого последовательность, которая возникает из первой теоремы об изоморфизме, есть
(здесь обозначена тривиальная группа , поскольку эти группы не должны быть абелевыми ).
Более конкретный пример точной последовательности на конечных группах:
где — циклическая группа порядка n , а — диэдральная группа порядка 2 n , которая является неабелевой группой.
Пересечение и сумма модулей
Пусть I и J — два идеала кольца R. Тогда
представляет собой точную последовательность R -модулей, где гомоморфизм модулей отображает каждый элемент x из в элемент прямой суммы , а гомоморфизм отображает каждый элемент из в .
Эти гомоморфизмы являются ограничениями аналогично определенных гомоморфизмов, которые образуют короткую точную последовательность
Переход к фактор-модулям дает другую точную последовательность
Характеристики
Лемма о расщеплении утверждает, что для короткой точной последовательности
- следующие условия эквивалентны.
- Существует морфизм t : B → A такой, что t ∘ f является тождеством на A .
- Существует морфизм u : C → B такой, что g ∘ u является тождественным на C .
- Существует морфизм u : C → B такой, что B является прямой суммой f ( A ) и u ( C ) .
Для некоммутативных групп лемма о расщеплении неприменима, и имеется только эквивалентность между двумя последними условиями, при этом «прямая сумма» заменяется на « полупрямое произведение ».
В обоих случаях говорят, что такая короткая точная последовательность расщепляется .
Лемма о змее показывает, как коммутативная диаграмма с двумя точными строками порождает более длинную точную последовательность. Лемма о девятке является частным случаем.
Лемма о пяти дает условия, при которых среднее отображение в коммутативной диаграмме с точными строками длины 5 является изоморфизмом; короткая лемма о пяти является ее частным случаем, применяемым к коротким точным последовательностям.
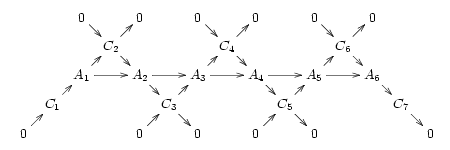
Лемма плетения
Важность коротких точных последовательностей подчеркивается тем фактом, что каждая точная последовательность является результатом «сплетения» нескольких перекрывающихся коротких точных последовательностей. Рассмотрим, например, точную последовательность
что подразумевает, что существуют объекты C k в категории такие, что
- .
Предположим дополнительно, что коядро каждого морфизма существует и изоморфно образу следующего морфизма в последовательности:
(Это верно для ряда интересных категорий, включая любую абелеву категорию, такую как абелевы группы; но это неверно для всех категорий, которые допускают точные последовательности, и, в частности, неверно для категории групп , в которой coker( f ) : G → H не является H /im( f ) , а представляет собой фактор H по сопряженному замыканию im( f ).) Затем мы получаем коммутативную диаграмму, в которой все диагонали являются короткими точными последовательностями:
Единственная часть этой диаграммы, которая зависит от условия коядра, — это объект и конечная пара морфизмов . Если существует какой-либо объект и морфизм, такой что является точным, то точность обеспечивается. Снова беря пример категории групп, тот факт, что im( f ) является ядром некоторого гомоморфизма на H, подразумевает, что это нормальная подгруппа , которая совпадает с ее сопряженным замыканием; таким образом, coker( f ) изоморфен образу H /im( f ) следующего морфизма.
И наоборот, если взять любой список перекрывающихся коротких точных последовательностей, их средние члены образуют точную последовательность таким же образом.
Применение точных последовательностей
В теории абелевых категорий короткие точные последовательности часто используются как удобный язык для обсуждения подобъектов и факторных объектов.
Проблема расширения по сути является вопросом «Данные конечные члены A и C короткой точной последовательности, какие возможности существуют для среднего члена B ?» В категории групп это эквивалентно вопросу, какие группы B имеют A как нормальную подгруппу и C как соответствующую фактор-группу? Эта проблема важна в классификации групп . См. также Outer automorphism group .
Обратите внимание, что в точной последовательности композиция f i +1 ∘ f i отображает A i в 0 в A i +2 , поэтому каждая точная последовательность является цепным комплексом . Более того, только f i -образы элементов A i отображаются в 0 с помощью f i +1 , поэтому гомология этого цепного комплекса тривиальна. Более кратко:
- Точные последовательности — это именно те цепочечные комплексы, которые являются ациклическими .
Таким образом, для любого цепочечного комплекса его гомологию можно рассматривать как меру степени его неточности.
Если мы возьмем ряд коротких точных последовательностей, связанных цепными комплексами (то есть короткую точную последовательность цепных комплексов, или с другой точки зрения, цепной комплекс коротких точных последовательностей), то мы можем вывести из этого длинную точную последовательность (то есть точную последовательность, индексированную натуральными числами) по гомологии, применяя лемму о зигзаге . Она возникает в алгебраической топологии при изучении относительной гомологии ; последовательность Майера–Виеториса является другим примером. Длинные точные последовательности, индуцированные короткими точными последовательностями, также характерны для производных функторов .
Точные функторы — это функторы , которые преобразуют точные последовательности в точные последовательности.
Ссылки
- Цитаты
- ^ "точная последовательность в nLab, примечание 2.3". ncatlab.org . Получено 2021-09-05 .
- Источники
- Спаниер, Эдвин Генри (1995). Алгебраическая топология . Берлин: Springer. стр. 179. ISBN 0-387-94426-5.
- Эйзенбуд, Дэвид (1995). Коммутативная алгебра: с видом на алгебраическую геометрию . Springer-Verlag New York. стр. 785. ISBN 0-387-94269-6.