Теорема Декарта

В геометрии теорема Декарта гласит, что для каждых четырёх целующихся или взаимно касающихся окружностей радиусы окружностей удовлетворяют определённому квадратному уравнению . Решая это уравнение, можно построить четвёртую окружность, касающуюся трёх данных взаимно касающихся окружностей. Теорема названа в честь Рене Декарта , который сформулировал её в 1643 году.

В стихотворении Фредерика Содди 1936 года «Точный поцелуй» теорема суммируется в терминах изгибов (обратных радиусов со знаком) четырех окружностей:

Сумма квадратов всех четырех изгибов
равна половине квадрата их суммы ^[1]

Особые случаи теоремы применяются, когда одна или две окружности заменяются прямой линией (с нулевым изгибом) или когда изгибы являются целыми числами или квадратными числами . Версия теоремы с использованием комплексных чисел позволяет вычислять центры окружностей, а не только их радиусы. При соответствующем определении кривизны теорема также применима в сферической геометрии и гиперболической геометрии . В более высоких измерениях аналогичное квадратное уравнение применяется к системам попарно касающихся сфер или гиперсфер.

Геометрические проблемы, связанные с касательными окружностями, обсуждались на протяжении тысячелетий. В Древней Греции в третьем веке до нашей эры Аполлоний Пергский посвятил этой теме целую книгу Ἐπαφαί [ Касательные окружности ]. Она была утеряна и известна в основном по описанию ее содержания Паппом Александрийским и по фрагментарным ссылкам на нее в средневековой исламской математике . ^[2] Однако греческая геометрия была в основном сосредоточена на построении линейки и циркуля . Например, задача Аполлония , тесно связанная с теоремой Декарта, требует построения окружности, касательной к трем данным окружностям, которые сами не обязательно должны быть касательными. ^[3] Вместо этого теорема Декарта сформулирована с использованием алгебраических соотношений между числами, описывающими геометрические формы. Это характерно для аналитической геометрии , области, пионерами которой были Рене Декарт и Пьер де Ферма в первой половине 17-го века. ^[4]

Декарт кратко обсудил проблему касательной окружности в 1643 году в двух письмах к принцессе Елизавете Пфальцской . ^[5] Первоначально Декарт поставил перед принцессой задачу Аполлония. После того, как частичные результаты Элизабет показали, что решение полной задачи аналитически было бы слишком утомительным, он упростил задачу до случая, в котором три заданные окружности являются взаимно касательными, и при решении этой упрощенной задачи он пришел к уравнению, описывающему связь между радиусами или кривизнами четырех попарно касающихся окружностей. Этот результат стал известен как теорема Декарта. ^{[6] [7]} Декарт не привел рассуждений, с помощью которых он нашел эту связь. ^[8]

Японская математика часто занималась проблемами, связанными с окружностями и их касаниями, ^[9] и японский математик Ямадзи Нусидзуми сформулировал форму теоремы Декарта об окружности в 1751 году. Как и Декарт, он выразил ее в виде полиномиального уравнения на радиусах, а не на их кривизнах. ^{[10] [11]} Частный случай этой теоремы для одной прямой линии и трех окружностей был записан на японской табличке сангаку 1824 года. ^[12]

Теорема Декарта была переоткрыта в 1826 году Якобом Штайнером ^[13] , в 1842 году Филиппом Бикрофтом ^[14] и в 1936 году Фредериком Содди . Содди решил оформить свою версию теоремы в виде стихотворения «Точный поцелуй» и опубликовал его в журнале Nature . Целующиеся окружности в этой задаче иногда называют окружностями Содди . Содди также распространил теорему на сферы ^[1] и в другом стихотворении описал цепочку из шести сфер, каждая из которых касается своих соседей и трех данных взаимно касающихся сфер, конфигурацию, которая теперь называется гекслетом Содди ^{[15] [16]} Торольд Госсет и несколько других распространили теорему и стихотворение на произвольные измерения; версия Госсета была опубликована в следующем году. ^{[17] [18]} Обобщение иногда называют теоремой Содди–Госсета , ^[19] хотя и гекслет, и трехмерная версия были известны ранее, в сангаку и в работе Роберта Лахлана 1886 года. ^{[12] [20] [21]}

Было опубликовано несколько доказательств теоремы. Доказательство Штайнера использует цепи Паппа и теорему Вивиани . Доказательства Филиппа Бикрофта и Х. С. М. Коксетера включают еще четыре окружности, проходящие через тройки касательных исходных трех окружностей; Коксетер также предоставил доказательство с использованием инверсной геометрии . Дополнительные доказательства включают аргументы, основанные на симметрии, вычислениях во внешней алгебре или алгебраических манипуляциях формулой Герона (для чего см. § Окружности Содди треугольника). ^{[22] [23]} Результат также следует из наблюдения, что определитель Кэли–Менгера четырех копланарных центров окружностей равен нулю. ^[24]

Теорему Декарта проще всего сформулировать в терминах кривизны окружностей . ^[25] Знаковая кривизна (или изгиб ) окружности определяется как ,${\displaystyle k=\pm 1/r}$ где - ее радиус. Чем больше окружность, тем меньше величина ее кривизны, и наоборот. Знак в (представленный символом ) положителен для окружности, которая касается снаружи других окружностей. Для касательной изнутри окружности, которая описывает другие окружности, знак отрицателен. Если прямая линия рассматривается как вырожденная окружность с нулевой кривизной (и, следовательно, бесконечным радиусом), теорема Декарта также применима к прямой и трем окружностям, которые все три касаются друг друга (см. Обобщенная окружность ). ^[1]${\displaystyle r}$${\displaystyle k=\pm 1/r}$${\displaystyle \pm }$

Для четырех окружностей, касающихся друг друга в шести различных точках, с кривизной , теорема Декарта гласит:${\displaystyle k_{i}}$ ${\displaystyle i=1,\dots ,4}$

${\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2\,(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2}).}$

${\displaystyle (1)}$

Если одна из четырех кривизн считается переменной, а остальные постоянными, то это квадратное уравнение . Чтобы найти радиус четвертой окружности, касательной к трем данным целующимся окружностям, квадратное уравнение можно решить как ^{[13] [26]}

${\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.}$

${\displaystyle (2)}$

Символ указывает, что в общем случае это уравнение имеет два решения, и любая тройка касательных окружностей имеет две касательные окружности (или вырожденные прямые линии). Критерии, специфичные для конкретной задачи, могут отдавать предпочтение одному из этих двух решений перед другим в любой данной задаче. ^[22]${\displaystyle \pm }$

Теорема неприменима к системам окружностей с более чем двумя окружностями, касающимися друг друга в одной точке. Она требует, чтобы точки касания были различны. ^[8] Когда более двух окружностей касаются друг друга в одной точке, может быть бесконечно много таких окружностей с произвольной кривизной; см. карандаш окружностей . ^[27]

Чтобы полностью определить окружность, необходимо знать не только ее радиус (или кривизну), но и ее центр. Соответствующее уравнение выражается наиболее ясно, если декартовы координаты интерпретировать как комплексное число . Тогда уравнение выглядит подобно теореме Декарта и поэтому называется комплексной теоремой Декарта . Если даны четыре окружности с кривизной и центрами для , в дополнение к уравнению (1) справедливо следующее равенство :${\displaystyle (x,y)}$ ${\displaystyle z=x+iy}$${\displaystyle k_{i}}$${\displaystyle z_{i}}$ ${\displaystyle i\in \{1,2,3,4\}}$

${\displaystyle (k_{1}z_{1}+k_{2}z_{2}+k_{3}z_{3}+k_{4}z_{4})^{2}=2\,(k_{1}^{2}z_{1}^{2}+k_{2}^{2}z_{2}^{2}+k_{3}^{2}z_{3}^{2}+k_{4}^{2}z_{4}^{2}).}$

${\displaystyle (3)}$

После того, как с помощью уравнения (2) найдено , можно приступить к вычислениям , решив уравнение (3) как квадратное уравнение, что приведет к форме, аналогичной уравнению (2) :${\displaystyle k_{4}}$${\displaystyle z_{4}}$

$${\displaystyle z_{4}={\frac {z_{1}k_{1}+z_{2}k_{2}+z_{3}k_{3}\pm 2{\sqrt {k_{1}k_{2}z_{1}z_{2}+k_{2}k_{3}z_{2}z_{3}+k_{1}k_{3}z_{1}z_{3}}}}{k_{4}}}.}$$

Опять же, в общем случае существует два решения для ,${\displaystyle z_{4}}$ соответствующих двум решениям для .${\displaystyle k_{4}}$ Знак плюс/минус в приведенной выше формуле для${\displaystyle z_{4}}$ не обязательно соответствует знаку плюс/минус в формуле для . ^{[19] [28] [29]}${\displaystyle k_{4}}$

Когда три из четырех окружностей конгруэнтны, их центры образуют равносторонний треугольник, как и их точки касания. Две возможности для четвертой окружности, касающейся всех трех, являются концентрическими, и уравнение (2) сводится к ^[30]

$${\displaystyle k_{4}=(3\pm 2{\sqrt {3}})k_{1}.}$$

Если одну из трех окружностей заменить прямой линией, касательной к оставшимся окружностям , то ее кривизна равна нулю и выпадает из уравнения (1). Например, если ,${\displaystyle k_{3}=0}$ то уравнение (1) можно разложить на множители как ^[31]

$${\displaystyle {\begin{aligned}&{\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{2}}}+{\sqrt {k_{4}}}{\bigr )}{\bigl (}{{\sqrt {k_{2}}}+{\sqrt {k_{4}}}-{\sqrt {k_{1}}}}{\bigr )}\\[3mu]&\quad {}\cdot {\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{4}}}-{\sqrt {k_{2}}}{\bigr )}{\bigl (}{\sqrt {k_{1}}}+{\sqrt {k_{2}}}-{\sqrt {k_{4}}}{\bigr )}=0,\end{aligned}}}$$

и уравнение (2) упрощается до ^[32]

$${\displaystyle k_{4}=k_{1}+k_{2}\pm 2{\sqrt {k_{1}k_{2}}}.}$$

Извлечение квадратного корня из обеих частей приводит к другой альтернативной формулировке этого случая (с ),${\displaystyle k_{1}\geq k_{2}}$

$${\displaystyle {\sqrt {k_{4}}}={\sqrt {k_{1}}}\pm {\sqrt {k_{2}}},}$$

что было описано как «своего рода безумная версия теоремы Пифагора ». ^[25]

Если две окружности заменить прямыми, касание между двумя замененными окружностями становится параллельностью между двумя заменяющими их прямыми. В этом случае, с , ${\displaystyle k_{2}=k_{3}=0}$ уравнение (2) сводится к тривиальному

$${\displaystyle \displaystyle k_{4}=k_{1}.}$$

Это соответствует наблюдению, что для того, чтобы все четыре кривые оставались взаимно касательными, две другие окружности должны быть конгруэнтными. ^{[19] [26]}

Когда четыре касательные окружности, описанные уравнением (2), все имеют целочисленные кривизны, альтернативная четвертая окружность, описанная вторым решением уравнения, также должна иметь целочисленную кривизну. Это происходит потому, что оба решения отличаются от целого числа на квадратный корень целого числа, и поэтому любое решение может быть целым числом только в том случае, если этот квадратный корень, а следовательно, и другое решение, также является целым числом. Каждые четыре целых числа, которые удовлетворяют уравнению в теореме Декарта, образуют кривизны четырех касательных окружностей. ^[33] Целочисленные четверки этого типа также тесно связаны с героновыми треугольниками , треугольниками с целочисленными сторонами и площадью. ^[34]

Начиная с любых четырех взаимно касающихся окружностей и многократно заменяя одну из четырех ее альтернативным решением ( прыжки Виета ) всеми возможными способами, получаем систему из бесконечного числа касающихся окружностей, называемую аполлоновой прокладкой . Когда исходные четыре окружности имеют целочисленные кривизны, то же самое происходит и с каждой заменой, и, следовательно, все окружности в прокладке имеют целочисленные кривизны. Любые четыре касающихся окружности с целочисленными кривизнами принадлежат ровно одной такой прокладке, однозначно описываемой ее корневой четверкой из четырех наибольших наибольших окружностей и четырех наименьших кривизн. Эту четверку можно найти, начиная с любой другой четверки из той же прокладки, многократно заменяя наименьшую окружность большей, которая решает то же самое уравнение Декарта, пока такое сокращение не станет возможным. ^[33]

Корневая четверка называется примитивной, если у нее нет нетривиального общего делителя . Каждая примитивная корневая четверка может быть найдена из факторизации суммы двух квадратов, , как четверка . Чтобы быть примитивной, она должна удовлетворять дополнительным условиям , и . Факторизации сумм двух квадратов могут быть получены с помощью теоремы о сумме двух квадратов . Любая другая целочисленная аполлоновская набивка может быть образована путем умножения примитивной корневой четверки на произвольное целое число, и любая четверка в одной из этих набивок (то есть любое целочисленное решение уравнения Декарта) может быть образована путем обращения процесса замены, используемого для нахождения корневой четверки. Например, набивка с корневой четверкой , показанная на рисунке, генерируется таким образом из факторизованной суммы двух квадратов . ^[33]${\displaystyle n^{2}+m^{2}=de}$${\displaystyle (-n,\,d+n,\,e+n,\,d+e+n-2m)}$${\displaystyle \gcd(n,d,e)=1}$ ${\displaystyle -n\leq 0\leq 2m\leq d\leq e}$${\displaystyle (-10,18,23,27)}$${\displaystyle 10^{2}+2^{2}=8\cdot 13}$

Частные случаи одной прямой линии и целочисленных кривизн объединяются в окружностях Форда . Это бесконечное семейство окружностей, касающихся оси -декартовой системы координат в ее рациональных точках. Каждая дробь (в низших членах) имеет окружность, касательную к прямой в точке с кривизной . Три из этих кривизн, вместе с нулевой кривизной оси, удовлетворяют условиям теоремы Декарта всякий раз, когда знаменатели двух соответствующих дробей в сумме дают знаменатель третьей. Две окружности Форда для дробей и (обе в низших членах) касаются, когда . Когда они касаются, они образуют четверку касательных окружностей с осью - и с окружностью для их медианы . ^[35]${\displaystyle x}$ ${\displaystyle p/q}$${\displaystyle (p/q,0)}$${\displaystyle 2q^{2}}$${\displaystyle p/q}$${\displaystyle r/s}$${\displaystyle |ps-qr|=1}$${\displaystyle x}$ ${\displaystyle (p+r)/(q+s)}$

Окружности Форда принадлежат специальному аполлоновскому уплотнению с корневой четверкой ,${\displaystyle (0,0,1,1)}$ ограниченному двумя параллельными линиями, которые могут быть приняты за ось - и линию . Это единственное аполлоновское уплотнение, содержащее прямую линию и не ограниченное окружностью отрицательной кривизны. Окружности Форда - это окружности в этом уплотнении, которые касаются оси - . ^[33]${\displaystyle x}$${\displaystyle y=1}$${\displaystyle x}$

Если четыре радиуса окружностей в теореме Декарта предполагаются в геометрической прогрессии с отношением ,${\displaystyle \rho }$ то кривизны также находятся в той же прогрессии (в обратном порядке). Подстановка этого отношения в теорему дает уравнение

$${\displaystyle 2(1+\rho ^{2}+\rho ^{4}+\rho ^{6})=(1+\rho +\rho ^{2}+\rho ^{3})^{2},}$$

которое имеет только одно действительное решение больше единицы, отношение

$${\displaystyle \rho =\varphi +{\sqrt {\varphi }}\approx 2.89005\ ,}$$

где — золотое сечение . Если та же самая прогрессия продолжается в обоих направлениях, каждые последовательные четыре числа описывают окружности, подчиняющиеся теореме Декарта. Полученная двусторонняя геометрическая прогрессия окружностей может быть организована в один спиральный узор касательных окружностей , называемый локсодромической последовательностью Коксетера касательных окружностей . Впервые она была описана вместе с аналогичными конструкциями в более высоких измерениях Х. С. М. Коксетером в 1968 году . ^{[36] [37]}${\displaystyle \varphi }$

Любой треугольник на плоскости имеет три внешне касающихся окружности с центрами в его вершинах. Пусть будет тремя точками, будут длинами противоположных сторон, и будет полупериметром , эти три окружности имеют радиусы . По теореме Декарта, еще две окружности, иногда называемые окружностями Содди , касаются этих трех окружностей. Они разделены вписанной окружностью , одна внутренняя по отношению к ней и одна внешняя. ^{[38] [39] [40]} Теорему Декарта можно использовать, чтобы показать, что кривизна внутренней окружности Содди равна , где - площадь треугольника, - его радиус описанной окружности , а - его радиус вписанной окружности . Внешняя окружность Содди имеет кривизну . ^[41] Внутренняя кривизна всегда положительна, но внешняя кривизна может быть положительной, отрицательной или нулевой. Треугольники, внешняя окружность которых вырождается в прямую линию с нулевой кривизной, называются «треугольниками Содди». ^[41]${\displaystyle A,B,C}$${\displaystyle a,b,c}$${\textstyle s={\tfrac {1}{2}}(a+b+c)}$${\displaystyle s-a,s-b,s-c}$${\textstyle (4R+r+2s)/\Delta }$${\displaystyle \Delta }$${\displaystyle R}$${\displaystyle r}$${\textstyle (4R+r-2s)/\Delta }$

Одно из многочисленных доказательств теоремы Декарта основано на этой связи с геометрией треугольника и на формуле Герона для площади треугольника как функции длин его сторон. Если три окружности касаются внешним образом, с радиусами , то их центры образуют вершины треугольника с длинами сторон и и полупериметром По формуле Герона этот треугольник имеет площадь${\displaystyle r_{1},r_{2},r_{3},}$${\displaystyle P_{1},P_{2},P_{3}}$${\displaystyle r_{1}+r_{2},}$ ${\displaystyle r_{1}+r_{3},}$${\displaystyle r_{2}+r_{3},}$${\displaystyle r_{1}+r_{2}+r_{3}.}$${\displaystyle \triangle P_{1}P_{2}P_{3}}$

$${\displaystyle {\sqrt {r_{1}r_{2}r_{3}(r_{1}+r_{2}+r_{3})}}.}$$

Теперь рассмотрим внутренний круг Содди с радиусом, центрированным в точке внутри треугольника. Треугольник можно разбить на три меньших треугольника , площади которых можно получить, подставив один из других радиусов в формулу площади выше. Площадь первого треугольника равна сумме этих трех площадей:${\displaystyle r_{4},}$${\displaystyle P_{4}}$${\displaystyle \triangle P_{1}P_{2}P_{3}}$${\displaystyle \triangle P_{1}P_{2}P_{4},}$ ${\displaystyle \triangle P_{4}P_{2}P_{3},}$${\displaystyle \triangle P_{1}P_{4}P_{3},}$${\displaystyle r_{4}}$

$${\displaystyle {\begin{aligned}{\sqrt {r_{1}r_{2}r_{3}(r_{1}+r_{2}+r_{3})}}={}&{\sqrt {r_{1}r_{2}r_{4}(r_{1}+r_{2}+r_{4})}}+{}\\&{\sqrt {r_{1}r_{3}r_{4}(r_{1}+r_{3}+r_{4})}}+{}\\&{\sqrt {r_{2}r_{3}r_{4}(r_{2}+r_{3}+r_{4})}}.\end{aligned}}}$$

Тщательные алгебраические вычисления показывают, что эта формула эквивалентна уравнению (1) , теореме Декарта. ^[22]

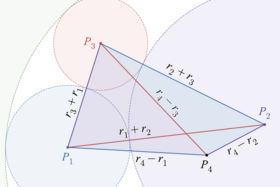
Этот анализ охватывает все случаи, в которых четыре окружности касаются внешне; одна из них всегда является внутренней окружностью Содди трех других. Случаи, в которых одна из окружностей касается внутренне трех других и образует их внешнюю окружность Содди, аналогичны. Снова четыре центра образуют четыре треугольника, но (пусть будет центром внешней окружности Содди) стороны треугольника, инцидентные ей, имеют длины, которые являются разностями радиусов, а не суммами. могут лежать внутри или снаружи треугольника, образованного тремя другими центрами; когда он находится внутри, площадь этого треугольника равна сумме площадей трех других треугольников, как указано выше. Когда он находится снаружи, четырехугольник, образованный четырьмя центрами, можно разделить диагональю на два треугольника двумя различными способами, что дает равенство между суммой площадей двух треугольников и суммой площадей двух других треугольников. В каждом случае уравнение площади сводится к теореме Декарта. Этот метод не применим напрямую к случаям, когда одна из окружностей вырождается в линию, но их можно рассматривать как предельный случай окружностей. ^[22]${\displaystyle P_{1},P_{2},P_{3},P_{4}}$${\displaystyle P_{4}}$${\displaystyle P_{4}}$${\displaystyle r_{4}-r_{1},}$ ${\displaystyle r_{4}-r_{1},}$${\displaystyle r_{4}-r_{3},}$${\displaystyle P_{4}}$

Теорему Декарта можно выразить в виде матричное уравнение, а затем обобщить на другие конфигурации четырех ориентированных окружностей , изменив матрицу. Пусть будет вектором-столбцом кривизны четырех окружностей, а будет симметричной матрицей , коэффициенты которой представляют относительную ориентацию между i -й и j -й ориентированными окружностями в точке их пересечения:${\displaystyle \mathbf {k} }$${\displaystyle \mathbf {Q} }$${\displaystyle q_{i,j}}$$${\displaystyle \mathbf {Q} ={\begin{bmatrix}{\phantom {-}}1&-1&-1&-1\\-1&{\phantom {-}}1&-1&-1\\-1&-1&{\phantom {-}}1&-1\\-1&-1&-1&{\phantom {-}}1\\\end{bmatrix}},\qquad \mathbf {Q} ^{-1}={\frac {1}{4}}{\begin{bmatrix}{\phantom {-}}1&-1&-1&-1\\-1&{\phantom {-}}1&-1&-1\\-1&-1&{\phantom {-}}1&-1\\-1&-1&-1&{\phantom {-}}1\\\end{bmatrix}}.}$$

Тогда уравнение (1) можно переписать в виде матричное уравнение ^{[19] [42]}

$${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =0.}$$

Как обобщение теоремы Декарта, модифицированная симметричная матрица может представлять любую желаемую конфигурацию из четырех окружностей, заменив каждый коэффициент наклоном между двумя окружностями, определяемым как${\displaystyle \mathbf {Q} }$ ${\displaystyle q_{i,j}}$

$${\displaystyle q_{i,j}={\frac {r_{i}^{2}+r_{j}^{2}-d_{i,j}^{2}}{2r_{i}r_{j}}},}$$

где — соответствующие радиусы окружностей, а — евклидово расстояние между их центрами. ^{[43] [44] [45]} Когда окружности пересекаются, , косинус угла пересечения между окружностями. Наклон, иногда называемый обратным расстоянием , имеет место , когда окружности касаются и ориентированы одинаково в точке касания, когда две окружности касаются и ориентированы противоположно в точке касания, для ортогональных окружностей , вне интервала для непересекающихся окружностей и в пределе, когда одна окружность вырождается в точку . ^{[42] [37]}${\displaystyle r_{i},r_{j}}$${\displaystyle d_{i,j}}$${\displaystyle q_{i,j}=\cos(\theta _{i,j})}$${\displaystyle 1}$${\displaystyle -1}$${\displaystyle 0}$${\displaystyle [-1,1]}$${\displaystyle \infty }$

Уравнение выполняется для любой произвольной конфигурации четырех окружностей на плоскости, при условии наличия соответствующей матрицы попарных наклонов. ^[42]${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =0}$${\displaystyle \mathbf {Q} }$

Теорема Декарта обобщается на взаимно касающиеся большие или малые окружности в сферической геометрии, если кривизна -й окружности определяется как геодезическая кривизна окружности относительно сферы, которая равна котангенсу ориентированного внутреннего радиуса. Тогда: ^{[19] [44]}${\displaystyle j}$${\textstyle k_{j}=\cot \rho _{j},}$ ${\displaystyle \rho _{j}.}$

$${\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2})+4.}$$

Решая одну из кривизн через три других,

$${\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}-1}}.}$$

Как матричное уравнение,

$${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =-1.}$$

Величина — это «стереографический диаметр» малого круга. Это евклидова длина диаметра в стереографически спроецированной плоскости, когда некоторая точка на круге проецируется в начало координат. Для большого круга такая стереографическая проекция — это прямая линия, проходящая через начало координат, поэтому . ^[46]${\displaystyle 1/k_{j}=\tan \rho _{j}}$${\displaystyle k_{j}=0}$

Аналогично, теорема обобщается на взаимно касающиеся окружности в гиперболической геометрии , если кривизна -го цикла определяется как геодезическая кривизна окружности относительно гиперболической плоскости, гиперболический котангенс ориентированного внутреннего радиуса Тогда: ^{[19] [44]}${\displaystyle j}$${\textstyle k_{j}=\coth \rho _{j},}$${\displaystyle \rho _{j}.}$

$${\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2})-4.}$$

Решая одну из кривизн через три других,

$${\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}+1}}.}$$

Как матричное уравнение,

$${\displaystyle \mathbf {k} ^{\mathsf {T}}\mathbf {Q} ^{-1}\mathbf {k} =1.}$$

Эта формула также справедлива для взаимно касательных конфигураций в гиперболической геометрии, включая гиперциклы и орициклы , если — геодезическая кривизна цикла относительно гиперболической плоскости, обратная величина стереографического диаметра цикла. Это диаметр при стереографической проекции ( модель диска Пуанкаре ), когда одна конечная точка диаметра проецируется в начало координат. ^[47] Гиперциклы не имеют четко определенного центра или внутреннего радиуса, а орициклы имеют идеальную точку для центра и бесконечный внутренний радиус, но для гиперболического круга, для орицикла, для гиперцикла и для геодезической . ^[48]${\displaystyle k_{j}}$${\displaystyle |k_{j}|>1}$${\displaystyle |k_{j}|=1}$${\displaystyle |k_{j}|<1}$${\displaystyle k_{j}=0}$

В -мерном евклидовом пространстве максимальное число взаимно касающихся гиперсфер равно . Например, в 3-мерном пространстве пять сфер могут быть взаимно касательными. Кривизны гиперсфер удовлетворяют${\displaystyle n}$${\displaystyle n+2}$

$${\displaystyle {\biggl (}\sum _{i=1}^{n+2}k_{i}{\biggr )}^{\!2}=n\,\sum _{i=1}^{n+2}k_{i}^{2}}$$

со случаем, соответствующим плоской гиперплоскости, обобщающим 2-мерную версию теоремы. ^{[19] [44]} Хотя не существует 3-мерного аналога комплексных чисел, соотношение между положениями центров можно переформулировать в виде матричного уравнения, которое также обобщается на размерности. ^[19]${\displaystyle k_{i}=0}$${\displaystyle n}$

В трех измерениях предположим, что три взаимно касающиеся сферы зафиксированы, и дана четвертая сфера, касательная к трем фиксированным сферам. Трехмерная версия теоремы Декарта может быть применена для нахождения сферы, касающейся и фиксированных сфер, затем применена снова для нахождения новой сферы, касающейся и фиксированных сфер, и так далее. Результатом является циклическая последовательность из шести сфер, каждая из которых касается своих соседей в последовательности и трех фиксированных сфер, конфигурация, названная гекслетом Содди , после открытия Содди и публикации ее в форме другого стихотворения в 1936 году. ^{[15] [16]}${\displaystyle S_{1}}$${\displaystyle S_{2}}$${\displaystyle S_{1}}$${\displaystyle S_{3}}$${\displaystyle S_{2}}$

Конфигурации более высоких размерностей взаимно касающихся гиперсфер в сферической или гиперболической геометрии с кривизной, определенной выше, удовлетворяют

$${\displaystyle {\biggl (}\sum _{i=1}^{n+2}k_{i}{\biggr )}^{\!2}=nC+n\,\sum _{i=1}^{n+2}k_{i}^{2},}$$

где в сферической геометрии и в гиперболической геометрии. ^{[44] [19]}${\displaystyle C=2}$${\displaystyle C=-2}$

• Упаковка круга в круг
• Четырехквадратное тождество Эйлера
• Круги Малфатти