Локсодромическая последовательность Коксетера касающихся окружностей

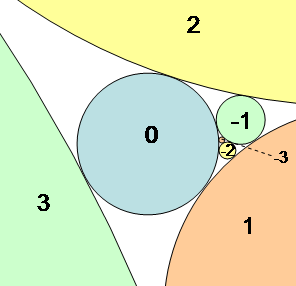
В геометрии локсодромическая последовательность Коксетера касательных окружностей — это бесконечная последовательность окружностей, расположенных так, что любые четыре последовательные окружности в последовательности попарно касаются друг друга. Это означает, что каждая окружность в последовательности касается трех предшествующих ей окружностей, а также трех следующих за ней окружностей.

Радиусы окружностей в последовательности образуют геометрическую прогрессию с отношением , где - золотое сечение . Это отношение и его обратная величина удовлетворяют уравнению , и поэтому любые четыре последовательных окружности в последовательности удовлетворяют условиям теоремы Декарта . ^{[1] [2]}$${\displaystyle k=\varphi +{\sqrt {\varphi }}\approx 2.89005\ ,}$$${\displaystyle \varphi}$${\displaystyle к}$$${\displaystyle (1+x+x^{2}+x^{3})^{2}=2(1+x^{2}+x^{4}+x^{6})\ ,}$$

Центры окружностей в последовательности лежат на логарифмической спирали . Если смотреть из центра спирали, угол между центрами последовательных окружностей равен ^[1] Угол между последовательными тройками центров такой же, как один из углов треугольника Кеплера , прямоугольного треугольника, построение которого также включает квадратный корень из золотого сечения. ^[3]$${\displaystyle \cos ^{-1}\left({\frac {-1}{\varphi }}\right)\approx 128.173^{\circ }\ .}$$$${\displaystyle \theta =\cos ^{-1}{\frac {1}{\varphi }}\approx 51,8273^{\circ },}$$

Конструкция названа в честь геометра Х. С. М. Коксетера , который обобщил двумерный случай на последовательности сфер и гиперсфер в более высоких измерениях. ^{[1] [4] [5]} Ее можно интерпретировать как вырожденный частный случай спирали Дойла . ^[2]

• Аполлоновская прокладка

• Вайсштейн, Эрик В. , «Локсодромическая последовательность Коксетера касательных окружностей», MathWorld