Теорема о сумме двух квадратов
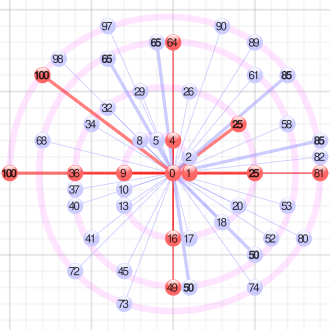
Характеристика простыми множителями сумм двух квадратов
Целые числа, удовлетворяющие теореме о сумме двух квадратов, являются квадратами возможных расстояний между целочисленными точками решетки; показаны значения до 100, при этом
• Квадраты (и, следовательно, целые расстояния) красного цвета, и
• Неуникальные представления (вплоть до поворота и отражения) выделены жирным шрифтом

В теории чисел теорема о сумме двух квадратов связывает разложение любого целого числа n > 1 на простые множители с тем , можно ли записать его в виде суммы двух квадратов , такой что n = a2 + b2 для некоторых целых чисел a , b . [1]

Целое число, большее единицы, можно записать в виде суммы двух квадратов тогда и только тогда, когда его разложение на простые числа не содержит множителей p k , где простое число , а k — нечетное . п ≡ 3 ( мод 4 ) {\displaystyle p\equiv 3{\pmod {4}}}

При записи числа в виде суммы двух квадратов допускается, чтобы один из квадратов был равен нулю или чтобы оба квадрата были равны друг другу, поэтому все квадраты и все двойные квадраты включены в числа, которые могут быть представлены таким образом. Эта теорема дополняет теорему Ферма о суммах двух квадратов , которая говорит, когда простое число может быть записано в виде суммы двух квадратов, в том смысле, что она также охватывает случай составных чисел .

Число может иметь несколько представлений в виде суммы двух квадратов, подсчитанных с помощью функции суммы квадратов ; например, каждая пифагорова тройка дает второе представление за пределами тривиального представления . а 2 + б 2 = с 2 {\displaystyle а^{2}+b^{2}=c^{2}} с 2 {\displaystyle c^{2}} с 2 + 0 2 {\displaystyle c^{2}+0^{2}}

Примеры

Разложение числа 2450 на простые числа дается формулой 2450 = 2  · 5 2  · 7 2 . Из простых чисел, встречающихся в этом разложении, 2, 5 и 7, только 7 сравнимо с 3 по модулю 4. Его показатель степени в разложении, 2, четный . Поэтому теорема утверждает, что его можно представить в виде суммы двух квадратов. Действительно, 2450 = 7 2 + 49 2 .

Разложение числа 3430 на простые множители равно 2  · 5  · 7 3 . На этот раз показатель степени числа 7 в разложении равен 3, нечетному числу. Поэтому 3430 нельзя записать в виде суммы двух квадратов.

Представимые числа

Числа, которые можно представить в виде суммы двух квадратов, образуют целочисленную последовательность [2]

0, 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26, 29, 32, ...

Они образуют множество всех норм целых гауссовых чисел ; [2] их квадратные корни образуют множество всех длин отрезков прямых между парами точек в двумерной целочисленной решетке .

Число представимых чисел в диапазоне от 0 до любого числа пропорционально , ​​с предельным коэффициентом пропорциональности, заданным константой Ландау–Рамануджана , приблизительно равным 0,764. [3] н {\displaystyle n} н бревно ⁡ н {\displaystyle {\frac {n}{\sqrt {\log n}}}}

Произведение любых двух представимых чисел есть другое представимое число. Его представление может быть получено из представлений его двух множителей, используя тождество Брахмагупты–Фибоначчи .

Теорема Якоби о двух квадратах

Теорема о двух квадратах  —  Обозначим число делителей как , а число этих делителей запишем через . Пусть , где . н {\displaystyle n} г ( н ) {\displaystyle d(n)} г а ( н ) {\displaystyle d_{a}(n)} г ≡ а мод 4 {\displaystyle d\equiv a{\bmod {4}}} н = 2 ф п 1 г 1 п 2 г 2 ⋯ д 1 с 1 д 2 с 2 ⋯ {\displaystyle n=2^{f}p_{1}^{r_{1}}p_{2}^{r_{2}}\cdots q_{1}^{s_{1}}q_{2}^{s_{2}}\cdots } п ≡ 1 мод 4 ,   д ≡ 3 мод 4 {\displaystyle p\equiv 1{\bmod {4}},\ q\equiv 3{\bmod {4}}}

г 2 ( н ) = 0 {\displaystyle r_{2}(n)=0} если какие-либо показатели нечетные. Если все четные, то с дж {\displaystyle s_{j}} с дж {\displaystyle s_{j}} г 2 ( н ) = 4 г ( п 1 г 1 п 2 г 2 ⋯ ) = 4 ( г 1 ( н ) − г 3 ( н ) ) {\displaystyle r_{2}(n)=4d(p_{1}^{r_{1}}p_{2}^{r_{2}}\cdots )=4(d_{1}(n)-d_{3}(n))}

Доказано Гауссом с использованием квадратичных форм и Якоби с использованием эллиптических функций . [4] Элементарное доказательство основано на уникальной факторизации гауссовых целых чисел . [4] Хиршхорн дает короткое доказательство, полученное из тройного произведения Якоби . [5]

Смотрите также

Ссылки

  1. ^ Дадли, Андервуд (1969). «Суммы двух квадратов». Элементарная теория чисел . WH Freeman and Company. стр. 135–139.
  2. ^ ab Sloane, N. J. A. (ред.). "Последовательность A001481 (Числа, являющиеся суммой 2 квадратов)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.
  3. ^ Ребак, Орс (2020). «Обобщение тождества Рамануджана». The American Mathematical Monthly . 127 (1): 80–83. arXiv : 1612.08307 . doi : 10.1080/00029890.2020.1668716. MR  4043992.
  4. ^ ab Grosswald, Emil (1985). Представления целых чисел в виде сумм квадратов . Нью-Йорк Берлин Гейдельберг [и т.д.]: Springer. С. 15–19. ISBN 978-3-540-96126-0.
  5. ^ Хиршхорн, Майкл (1985). «Простое доказательство теоремы Якоби о двух квадратах» (PDF) . Amer. Math. Monthly . 92 : 579–580.
Взято с "https://en.wikipedia.org/w/index.php?title=Теорема_о_сумме_двух_квадратов&oldid=1248460971"