Список интервалов высоты тона


Ниже приведен список интервалов, выражаемых через простой предел (см. Терминология), дополненный выбором интервалов в различных равных подразделениях октавы или других интервалов.
Для часто встречающихся гармонических или мелодических интервалов между парами нот в современной западной музыкальной теории , без учета способа их настройки, см. Интервал (музыка) § Основные интервалы .
Терминология
- Простой предел [1], далее именуемый просто пределом , является наибольшим простым числом , встречающимся в факторизациях числителя и знаменателя отношения частот, описывающего рациональный интервал. Например, предел только чистой кварты (4:3) равен 3, но только минорный тон (10:9) имеет предел 5, потому что 10 можно разложить на множители 2 × 5 (а 9 на 3 × 3 ). Существует другой тип предела, нечетный предел , концепция, используемая Гарри Парчем (больше нечетных чисел, полученных после деления числителя и знаменателя на максимально возможные степени 2), но здесь она не используется. Термин «предел» был придуман Парчем. [1]
- По определению, каждый интервал в данном пределе может быть также частью предела более высокого порядка. Например, блок с 3 пределами может быть также частью настройки с 5 пределами и т. д. Сортируя столбцы пределов в таблице ниже, можно объединить все интервалы данного предела (сортировка в обратном порядке путем двойного нажатия кнопки).
- Пифагорейский строй означает интонацию с тремя пределами — отношение чисел с простыми множителями не выше трех.
- Просто интонация означает интонацию с пределом 5 — отношение чисел с простыми множителями не выше пяти.
- Септимальная , ундецимальная , тридесятичная и септендесятичная системы означают соответственно 7-, 11-, 13- и 17-предельную интонацию.
- Meantone относится к meantone темперации , где весь тон является средним значением большой терции. В общем, meantone строится так же, как и пифагорейская настройка, как стек квинт: тон достигается после двух квинт, большая терция после четырех, так что, поскольку все квинты одинаковы, тон является средним значением терции. В meantone темперации каждая квинта сужается («темперируется») на одинаковую небольшую величину. Наиболее распространенной из meantone темперацией является meantone с четвертной комой , в которой каждая квинта темперируется на 1 ⁄ 4 синтонической коммы, так что после четырех шагов большая терция (как CGDAE) является полной синтонической коммой ниже пифагорейской. Крайности систем meantone, встречающиеся в исторической практике, — это пифагорейская настройка, где весь тон соответствует 9:8, т. е . (3:2) 2/2 , среднее значение большой терции (3:2) 4/4 , и квинта (3:2) не темперирована; и 1 ⁄ 3 -комма означает тон, где квинта темперирована до такой степени, что три восходящие квинты дают чистую минорную терцию. (См. темперации meanone ). Музыкальная программа Logic Pro также использует темперацию 1 ⁄ 2 -комма означает тон.
- Равномерно темперированный строй — это строй с X тонами и интервалами, соответствующими X делениям на октаву.
- Однако темперированные интервалы не могут быть выражены в терминах простых пределов и, если нет исключений, не указаны в таблице ниже.
- Таблицу также можно сортировать по частоте, по центам или в алфавитном порядке.
- Суперчастные отношения — это интервалы, которые можно выразить как отношение двух последовательных целых чисел.
Список
| Столбец | Легенда |
|---|---|
| ТЕТ | X -тоновая равномерная темперация (12-тет и т. д.). |
| Предел | 3- предельная интонация, или пифагорейская . |
| 5 - ограничить интонацию «только», или просто . | |
| 7 -предельная интонация, или септимальная . | |
| 11 - предельная интонация, или недесятичная . | |
| 13- предельная интонация, или трехзначная . | |
| 17 -предельная интонация, или семнадцатеричная . | |
| 19- предельная интонация, или новендецимальная . | |
| Более высокие пределы. | |
| М | Среднетоновая темперация или настройка. |
| С | Сверхчастное отношение (отдельного цветового кода нет). |
| Центы | Примечание (из C) | Частотное отношение | Простые множители | Название интервала | ТЕТ | Предел | М | С |
|---|---|---|---|---|---|---|---|---|
0.00 | С [2] | 1 : 1 | 1 : 1 | Унисон , [3] монофония, [4] совершенный прим, [3] тоника , [5] или фундаментальный | 1, 12 | 3 | М | |
0,03 | 65537 : 65536 | 65537 : 2 16 | Шестьдесят пять тысяч пятьсот тридцать седьмая гармоника | 65537 | С | |||
0,40 | С ♯ − ♯ − | 4375 : 4374 | 5 4 ×7 : 2×3 7 | Рагизма [3] [6] | 7 | С | ||
0,72 | Э     + + | 2401 : 2400 | 7 4 : 2 5 ×3×5 2 | Бридсма [3] [6] | 7 | С | ||
1.00 | 2 1/1200 | 2 1/1200 | Цент [7] | 1200 | ||||
1.20 | 2 1/1000 | 2 1/1000 | Миллиоктава | 1000 | ||||
1.95 | Б ♯ ++ | 32805 : 32768 | 3 8 ×5 : 2 15 | Раскол [3] [5] | 5 | |||
1.96 | 3:2÷(2 7/12 ) | 3 : 2 19/12 | Град , Веркмейстер [8] | |||||
3.99 | 10 1/1000 | 2 1/1000 ×5 1/1000 | Савар или эптамерид | 301.03 | ||||
7.71 | Б ♯ ♯ | 225 : 224 | 3 2 ×5 2 : 2 5 ×7 | Септимальная клейсма , [3] [6] чудо-запятая | 7 | С | ||
8.11 | Б − − | 15625 : 15552 | 5 6 : 2 6 ×3 5 | Клейсма или мажор с запятой [3] [6] | 5 | |||
10.06 | А  ++ ++ | 2109375 : 2097152 | 3 3 ×5 7 : 2 21 | Запятая , [3] [6] Запятая Фоккера [3] | 5 | |||
10.85 | С | 160 : 159 | 2 5 ×5 : 3×53 | Разница между 5:3 и 53:32 | 53 | С | ||
11.98 | С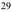 | 145 : 144 | 5×29 : 2 4 ×3 2 | Разница между 29:16 и 9:5 | 29 | С | ||
12.50 | 2 1/96 | 2 1/96 | Шестнадцатый тон | 96 | ||||
13.07 | Б   − − | 1728 : 1715 | 2 6 ×3 3 : 5×7 3 | Запятая Оруэлла [3] [9] | 7 | |||
13.47 | С | 129 : 128 | 3×43 : 2 7 | Сто двадцать девятая гармоника | 43 | С | ||
13.79 | Д  | 126 : 125 | 2×3 2 ×7 : 5 3 | Малая семеричная запятая , [6] малая семеричная запятая, [3] скворцовая запятая | 7 | С | ||
14.37 | С ♭ ↑ ↑ − | 121 : 120 | 11 2 : 2 3 ×3×5 | Недесятичные секунды запятая [3] | 11 | С | ||
16.67 | С ↑ [а] | 2 1/72 | 2 1/72 | 1 шаг из 72 равномерно темперированных ладов | 72 | |||
18.13 | С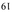 | 96 : 95 | 2 5 ×3 : 5×19 | Разница между 19:16 и 6:5 | 19 | С | ||
19.55 | Д -- [2] -- [2] | 2048 : 2025 | 2 11 : 3 4 ×5 2 | Диашисма , [3] [6] малая запятая | 5 | |||
21.51 | С+ [2] | 81 : 80 | 3 4 : 2 4 ×5 | Синтоническая запятая , [3] [5] [6] большая запятая, комма, хроматическая диеза или запятая Дидима [3] [6] [10] [11] | 5 | С | ||
22.64 | 2 1/53 | 2 1/53 | Холдеровская запятая , Холдеровская запятая, 1 шаг из 53 равномерно темперированных ладов | 53 | ||||
23.46 | В ♯ +++ | 531441 : 524288 | 3 12 : 2 19 | Пифагорейская запятая , [3] [5] [6] [10] [11] дитоническая запятая [3] [6] | 3 | |||
25.00 | 2 1/48 | 2 1/48 | Восьмой тон | 48 | ||||
26.84 | С | 65 : 64 | 5×13 : 2 6 | Шестьдесят пятая гармоника, [5] 13-я парциальная цветность [3] | 13 | С | ||
27.26 | С − − | 64 : 63 | 2 6 : 3 2 ×7 | Септимальная запятая , [3] [6] [11] Архитова запятая, [3] 63-я субгармоника | 7 | С | ||
29.27 | 2 1/41 | 2 1/41 | 1 шаг из 41 равномерно темперированного строя | 41 | ||||
31.19 | Д ♭ ↓ ♭ ↓ | 56 : 55 | 2 3 ×7 : 5×11 | Недесятичный диезис, [3] энгармонизм Птолемея: [5] разница между (11 : 8) и (7 : 5) тритоном | 11 | С | ||
33.33 | С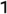 /Д ♭ /Д ♭  [а] [а] | 2 1/36 | 2 1/36 | Шестой тон | 36, 72 | |||
34.28 | С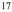 | 51 : 50 | 3×17 : 2×5 2 | Разница между 17:16 и 25:24 | 17 | С | ||
34.98 | Б  ♯ - ♯ - | 50 : 49 | 2×5 2 : 7 2 | Семитональный шестой тон или юбилизм, декатональная комма Эрлиха или тритонический диезис [3] [6] | 7 | С | ||
35.70 | Д  ♭ ♭ | 49 : 48 | 7 2 : 2 4 ×3 | Септимальный диезис , слендродиезис или септимальный 1/6-тон [3] | 7 | С | ||
38.05 | С | 46 : 45 | 2×23 : 3 2 ×5 | Низшая четверть тона, [5] разница между 23:16 и 45:32 | 23 | С | ||
38.71 | 2 1/31 | 2 1/31 | 1 шаг из 31 равномерной темперации или Нормальный Диезис | 31 | ||||
38.91 | С ↓ ♯ + | 45 : 44 | 3 2 ×5 : 4×11 | Недесятичный диез или недесятичный квинтовый тон | 11 | С | ||
40.00 | 2 1/30 | 2 1/30 | Пятый тон | 30 | ||||
41.06 | Д − − | 128 : 125 | 2 7 : 5 3 | Энгармонический диезис или 5-предельная лимма, малый диезис, [6] уменьшенная секунда, [5] [6] малый диезис или диезис, [3] 125-я субгармоника | 5 | |||
41.72 | Д  ♭ ♭ | 42 : 41 | 2×3×7 : 41 | Малый 41-й предельный квинтовый тон | 41 | С | ||
42.75 | С | 41 : 40 | 41 : 2 3 ×5 | Большой 41-предельный квинтовый тон | 41 | С | ||
43.83 | С ♯ ♯ | 40 : 39 | 2 3 ×5 : 3×13 | Тридецимальный пятый тон | 13 | С | ||
44.97 | С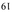  | 39 : 38 | 3×13 : 2×19 | Верхний четвертьтон, [5] новендецимальный квинтовый тон | 19 | С | ||
46.17 | Д   - - | 38 : 37 | 2×19 : 37 | Меньший 37-й предел четверти тона | 37 | С | ||
47.43 | С ♯ ♯ | 37 : 36 | 37 : 2 2 ×3 2 | Более 37-предельная четверть тона | 37 | С | ||
48.77 | С | 36 : 35 | 2 2 ×3 2 : 5×7 | Септимальный четверть тона , септимальный диезис, [3] [6] септимальная цветность, [2] верхний четверть тона [5] | 7 | С | ||
49.98 | 246 : 239 | 3×41 : 239 | Всего четверть тона [11] | 239 | ||||
50.00 | С /Д /Д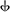 | 2 1/24 | 2 1/24 | Равномерно темперированный четверть тона | 24 | |||
50.18 | Д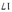  ♭ ♭ | 35 : 34 | 5×7 : 2×17 | ET четвертьтоновое приближение, [5] меньший 17-предельный четвертьтон | 17 | С | ||
50.72 | Б ♯ + + ♯ + + | 59049 : 57344 | 3 10 : 2 13 ×7 | Запятая Гаррисона (10 P5 – 1 H7) [3] | 7 | |||
51.68 | С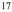 ↓ ♯ ↓ ♯ | 34 : 33 | 2×17 : 3×11 | Более 17-ти четвертной тон | 17 | С | ||
53.27 | С ↑ | 33 : 32 | 3×11 : 2 5 | Тридцать третья гармоника, [5] недесятичная запятая, недесятичная четверть тона | 11 | С | ||
54.96 | Д ♭ - ♭ - | 32 : 31 | 2 5 : 31 | Низшая четверть тона, [5] тридцать первая субгармоника | 31 | С | ||
56.55 | Б  ♯ + ♯ + | 529 : 512 | 23 2 : 2 9 | Пятьсот двадцать девятая гармоника | 23 | |||
56.77 | С | 31 : 30 | 31 : 2×3×5 | Больше четверти тона, [5] разница между 31:16 и 15:8 | 31 | С | ||
58.69 | С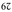 ♯ ♯ | 30 : 29 | 2×3×5 : 29 | Меньший предел 29 четверть тона | 29 | С | ||
60,75 | С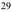  | 29 : 28 | 29 : 2 2 ×7 | Более 29-ти тактовый предел | 29 | С | ||
62.96 | Д ♭ - ♭ - | 28 : 27 | 2 2 ×7 : 3 3 | Септимальная малая секунда, малая малая секунда, нижняя четверть тона [5] | 7 | С | ||
63,81 | (3 : 2) 1/11 | 3 1/11 : 2 1/11 | Шаг шкалы бета | 18.75 | ||||
65.34 | С ♯ + ♯ + | 27 : 26 | 3 3 : 2×13 | Хроматический диезис , [12] трёхдесятичная запятая [3] | 13 | С | ||
66.34 | Д  ♭ ♭ | 133 : 128 | 7×19 : 2 7 | Сто тридцать третья гармоника | 19 | |||
66.67 | С ↑ /С ♯ ↑ /С ♯ [а] [а] | 2 1/18 | 2 1/18 | Третий тон | 18, 36, 72 | |||
67.90 | Д  - - | 26 : 25 | 2×13 : 5 2 | Тридецимальный третий тон, третий тон [5] | 13 | С | ||
70,67 | С ♯ [2] | 25 : 24 | 5 2 : 2 3 ×3 | Только хроматический полутон или минорная хрома, [3] меньший хроматический полутон, малый (только) полутон [11] или малая секунда, [4] малый хроматический полутон, [13] или минорный полутон, [5] 2 ⁄ 7 - запятая означает один хроматический полутон, увеличенный унисон | 5 | С | ||
73,68 | Д ♭ - ♭ - | 24 : 23 | 2 3 ×3 : 23 | Меньший 23-й предельный полутон | 23 | С | ||
75.00 | 2 1/16 | 2 3/48 | 1 шаг из 16 равномерно темперированных ладов, 3 шага из 48 | 16, 48 | ||||
76.96 | С ↓ ♯ + ↓ ♯ + | 23 : 22 | 23 : 2×11 | Больше 23-го предела полутона | 23 | С | ||
78.00 | (3 : 2) 1/9 | 3 1/9 : 2 1/9 | Шаг шкалы альфа | 15.39 | ||||
79.31 | 67 : 64 | 67 : 2 6 | Шестьдесят седьмая гармоника [5] | 67 | ||||
80,54 | С ↑ - - | 22 : 21 | 2×11 : 3×7 | Твёрдый полутон, [5] двухквинтовый тон малый полутон | 11 | С | ||
84.47 | Д ♭ ♭ | 21 : 20 | 3×7 : 2 2 ×5 | Септимальный хроматический полутон , минорный полутон [3] | 7 | С | ||
88.80 | С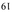 ♯ ♯ | 20 : 19 | 2 2 ×5 : 19 | Новендецимальный увеличенный унисон | 19 | С | ||
90.22 | Д ♭ −− [2] | 256 : 243 | 2 8 : 3 5 | Пифагорейская малая секунда или лимма , [3] [6] [11] Пифагорейский диатонический полутон, низкий полутон [14] | 3 | |||
92.18 | С ♯ + [2] | 135 : 128 | 3 3 ×5 : 2 7 | Большой хроматический полутон, хроматический полутон, средний полутон, большая хрома или большая лимма, [3] малая лимма, [11] большой хроматический полутон, [13] восходящая лимма [5] | 5 | |||
93.60 | Д ♭ - ♭ - | 19 : 18 | 19 : 2×9 | Новендецимальная малая секунда | 19 | С | ||
97.36 | Д↓↓ | 128 : 121 | 2 7 : 11 2 | 121-я субгармоника, [5] [6] недесятичная малая секунда | 11 | |||
98.95 | Д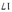 ♭ ♭ | 18 : 17 | 2×3 2 : 17 | Только малый полутон, указательный палец арабской лютни [3] | 17 | С | ||
100.00 | С ♯ /Д ♭ | 2 1/12 | 2 1/12 | Равномерно темперированная малая секунда или полутон | 12 | М | ||
104.96 | С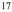 ♯ [2] ♯ [2] | 17 : 16 | 17 : 2 4 | Минорный диатонический полутон , только мажорный полутон, обертоновый полутон, [5] 17-я гармоника, [3] лимма [ необходима ссылка ] | 17 | С | ||
111.45 | 25 √ 5 | (5 : 1) 1/25 | Интервал Study II (сложная большая терция, 5:1, разделенная на 25 равных частей) | 25 | ||||
111.73 | Д ♭ - [2] | 16 : 15 | 2 4 : 3×5 | Только малая секунда , [15] только диатонический полутон , большая только полутон или большая секунда, [4] большой полутон, [5] лимма, малая диатоническая секунда, [3] диатоническая секунда [16] полутон, [14] диатонический полутон, [11] 1 ⁄ 6 - запятая означает одну малую секунду | 5 | С | ||
113.69 | С ♯ ++ | 2187 : 2048 | 3 7 : 2 11 | Апотом [3] [11] или пифагорейский большой полутон, [6] пифагорейский увеличенный унисон , пифагорейский хроматический полутон или пифагорейский апотом | 3 | |||
116.72 | (18 : 5) 1/19 | 2 1/19 ×3 2/19 : 5 1/19 | Секор | 10.28 | ||||
119.44 | С ♯ ♯ | 15 : 14 | 3×5 : 2×7 | Септимальный диатонический полутон , мажорный диатонический полутон, [3] полутон Коуэлла [5] | 7 | С | ||
125.00 | 2 5/48 | 2 5/48 | 5 шагов в 48 равномерно темперированных ладах | 48 | ||||
128.30 | Д  | 14 : 13 | 2×7 : 13 | Малый трехзначный 2/3-тон [17] | 13 | С | ||
130.23 | С ♯ + ♯ + | 69 : 64 | 3×23 : 2 6 | Шестьдесят девятая гармоника [5] | 23 | |||
133.24 | Д ♭ | 27 : 25 | 3 3 : 5 2 | Полутон максимальный , малая секунда, большая лимма или малый полутон Болена-Пирса, [3] высокий полутон, [14] альтернативный ренессансный полутон, [5] большая лимма, острая малая секунда [ требуется ссылка ] | 5 | |||
133.33 | С ♯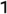 /Д ♭ /Д ♭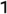 [а] [а] | 2 1/9 | 2 2/18 | Две трети тона | 9, 18, 36, 72 | |||
138,57 | Д ♭ - ♭ - | 13 : 12 | 13 : 2 2 ×3 | Большой тридецимальный 2/3-тон, [17] Три четверти тона [5] | 13 | С | ||
150.00 | С /Д /Д | 2 3/24 | 2 1/8 | Равномерно темперированный нейтральный второй | 8, 24 | |||
150,64 | Д↓ [2] | 12 : 11 | 2 2 ×3 : 11 | 3 ⁄ тона или недесятичная нейтральная секунда , [3] [5] труба три четверти тона, [11] средний палец [между ладами] [14] | 11 | С | ||
155.14 | Д | 35 : 32 | 5×7 : 2 5 | Тридцать пятая гармоника [5] | 7 | |||
160.90 | Д−− | 800 : 729 | 2 5 ×5 2 : 3 6 | Середина тональности [3], нейтральная секунда, середина тональности [ требуется ссылка ] | 5 | |||
165.00 | Д ↑ ♭ − [2] | 11 : 10 | 11 : 2×5 | Большая недесятичная минорная/мажорная/ нейтральная секунда , 4/5-тон [6] или секунда Птолемея [3] | 11 | С | ||
171.43 | 2 1/7 | 2 1/7 | 1 шаг из 7 равномерно темперированных ладов | 7 | ||||
175.00 | 2 7/48 | 2 7/48 | 7 шагов в 48 равномерно темперированных ладах | 48 | ||||
179,70 | 71 : 64 | 71 : 2 6 | Семьдесят первая гармоника [5] | 71 | ||||
180,45 | Э −−− −−− | 65536 : 59049 | 2 16 : 3 10 | Пифагорейская уменьшенная терция , [3] [6] Пифагорейский минорный тон | 3 | |||
182.40 | Д− [2] | 10 : 9 | 2×5 : 3 2 | Малый целый тон или большая секунда, [4] малый целый тон, [3] [5] малый целый тон, [16] малый тон, [14] малая секунда, [11] полузапятая означает одну большую секунду | 5 | С | ||
200.00 | Д | 2 2/12 | 2 1/6 | Равномерно темперированный мажорный второй строй | 6, 12 | М | ||
203.91 | Д [2] | 9 : 8 | 3 2 : 2 3 | Пифагорейская большая секунда , большой целый тон или большая секунда [11] (полутораоктава), [4] тон , большой целый тон, [3] [5] большой целый тон, [16] большой тон [14] | 3 | С | ||
215.89 | Д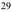 | 145 : 128 | 5×29 : 2 7 | Сто сорок пятая гармоника | 29 | |||
223.46 | Э − [2] − [2] | 256 : 225 | 2 8 : 3 2 ×5 2 | Только что уменьшенная третья , [16] 225-я субгармоника | 5 | |||
225.00 | 2 3/16 | 2 9/48 | 9 шагов в 48 равномерно темперированных ладах | 16, 48 | ||||
227.79 | 73 : 64 | 73 : 2 6 | Семьдесят третья гармоника [5] | 73 | ||||
231.17 | Д − [2] − [2] | 8 : 7 | 2 3 : 7 | Септимальная большая секунда , [4] септимальный целый тон [3] [5] | 7 | С | ||
240.00 | 2 1/5 | 2 1/5 | 1 шаг из 5 равномерно темперированных | 5 | ||||
247.74 | Д ♯ ♯ | 15 : 13 | 3×5 : 13 | Тридецимальный 5 ⁄ тона [3 ] | 13 | |||
250.00 | Д /Э /Э | 2 5/24 | 2 5/24 | 5 шагов в 24 равномерно темперированных ладах | 24 | |||
251.34 | Д ♯ ♯ | 37 : 32 | 37 : 2 5 | Тридцать седьмая гармоника [5] | 37 | |||
253.08 | Д ♯ − | 125 : 108 | 5 3 : 2 2 ×3 3 | Полуувеличенный целый тон, [3] полуувеличенная секунда [ требуется ссылка ] | 5 | |||
262.37 | Э↓ ♭ | 64 : 55 | 2 6 : 5×11 | 55-я субгармоника [5] [6] | 11 | |||
266.87 | Э ♭ [2] ♭ [2] | 7 : 6 | 7 : 2×3 | Септимальная малая терция [3] [4] [11] или субмалая терция [14] | 7 | С | ||
268.80 | Д  | 299 : 256 | 13×23 : 2 8 | Двести девяносто девятая гармоника | 23 | |||
274,58 | Д ♯ [2] | 75 : 64 | 3×5 2 : 2 6 | Только что увеличенная секунда , [16] Увеличенный тон, [14] увеличенная секунда [5] [13] | 5 | |||
275.00 | 2 11/48 | 2 11/48 | 11 шагов в 48 равномерно темперированных ладах | 48 | ||||
289.21 | Э ↓ ♭ ↓ ♭ | 13 : 11 | 13 : 11 | Тридесятичная малая терция [3] | 13 | |||
294.13 | Э ♭ − [2] | 32 : 27 | 2 5 : 3 3 | Пифагорейская малая терция [3] [5] [6] [14] [16] полудитон , или 27-я субгармоника | 3 | |||
297.51 | Э ♭ [2] ♭ [2] | 19 : 16 | 19 : 2 4 | 19-я гармоника, [3] 19-предельная малая терция, обертонная малая терция [5] | 19 | |||
300.00 | Д ♯ /Э ♭ | 2 3/12 | 2 1/4 | Равномерно темперированная малая терция | 4, 12 | М | ||
301.85 | Д ♯ - ♯ - | 25 : 21 [5] | 5 2 : 3×7 | Квазиравномерно темперированная малая терция, вторая малая терция с 7-м пределом, секунда Болена-Пирса [3] [6] | 7 | |||
310.26 | 6:5÷(81:80) 1/4 | 2 2 : 5 3/4 | Четверть запятой означала одну малую терцию | М | ||||
311.98 | (3 : 2) 4/9 | 3 4/9 : 2 4/9 | Альфа гамма минорная терция | 3.85 | ||||
315.64 | Э ♭ [2] | 6 : 5 | 2×3 : 5 | Просто малая терция , [3] [4] [5] [11] [16] малая терция, [14] 1 ⁄ 3 - запятая означает одну малую терцию | 5 | М | С | |
317.60 | D ♯ ++ | 19683 : 16384 | 3 9 : 2 14 | Пифагорейская увеличенная секунда [3] [6] | 3 | |||
320.14 | Э ♭ ↑ ♭ ↑ | 77 : 64 | 7×11 : 2 6 | Семьдесят седьмая гармоника [5] | 11 | |||
325.00 | 2 13/48 | 2 13/48 | 13 шагов в 48 равномерно темперированных ладах | 48 | ||||
336.13 | Д  ♯ - ♯ - | 17 : 14 | 17 : 2×7 | Суперминорная терция [18] | 17 | |||
337.15 | Э ♭ + | 243 : 200 | 3 5 : 2 3 ×5 2 | Акута малая терция [3] | 5 | |||
342.48 | Э ♭ ♭ | 39 : 32 | 3×13 : 2 5 | Тридцать девятая гармоника [5] | 13 | |||
342.86 | 2 2/7 | 2 2/7 | 2 шага в 7 равномерно темперированных ладах | 7 | ||||
342.91 | Э ♭ - ♭ - | 128 : 105 | 2 7 : 3×5×7 | 105-я субгармоника, [5] семимальная нейтральная треть [6] | 7 | |||
347.41 | Э ↑ ♭ − [2] | 11 : 9 | 11 : 3 2 | Нейтральная третья часть десятичной дроби [3] [5] | 11 | |||
350.00 | Д /Э /Э | 2 7/24 | 2 7/24 | Равномерно темперированная нейтральная терция | 24 | |||
354,55 | Э ↓ + | 27 : 22 | 3 3 : 2×11 | Воста Залзала [6] 12:11 X 9:8 [14] | 11 | |||
359.47 | Э [2] [2] | 16 : 13 | 2 4 : 13 | Тридесятичная нейтральная треть [3] | 13 | |||
364,54 | 79 : 64 | 79 : 2 6 | Семьдесят девятая гармоника [5] | 79 | ||||
364,81 | Е− | 100 : 81 | 2 2 ×5 2 : 3 4 | Грейв мажор терция [3] | 5 | |||
375.00 | 2 5/16 | 2 15/48 | 15 шагов в 48 равномерно темперированных ладах | 16, 48 | ||||
384.36 | Ф ♭ −− | 8192 : 6561 | 2 13 : 3 8 | Пифагорейская уменьшенная кварта , [3] [6] Пифагорейская «раскольническая» терция [5] | 3 | |||
386.31 | Э [2] | 5 : 4 | 5 : 2 2 | Просто большая терция , [3] [4] [5] [11] [16] большая терция, [14] четверть запятой означает одну большую терцию | 5 | М | С | |
397.10 | Э  + + | 161 : 128 | 7×23 : 2 7 | Сто шестьдесят первая гармоника | 23 | |||
400.00 | Э | 2 4/12 | 2 1/3 | Равномерно темперированная большая терция | 3, 12 | М | ||
402.47 | Э  | 323 : 256 | 17×19 : 2 8 | Триста двадцать третья гармоника | 19 | |||
407.82 | Е+ [2] | 81 : 64 | 3 4 : 2 6 | Пифагорейская большая терция , [3] [5] [6] [14] [16] дитон | 3 | |||
417.51 | Ф ↓ + [2] ↓ + [2] | 14 : 11 | 2×7 : 11 | Недесятичная уменьшенная кварта или большая терция [3] | 11 | |||
425.00 | 2 17/48 | 2 17/48 | 17 шагов в 48 равномерно темперированных ладах | 48 | ||||
427.37 | Ф ♭ [2] | 32 : 25 | 2 5 : 5 2 | Только что уменьшенная кварта , [16] уменьшенная кварта, [5] [13] 25-я субгармоника | 5 | |||
429.06 | Э | 41 : 32 | 41 : 2 5 | Сорок первая гармоника [5] | 41 | |||
435.08 | Э [2] [2] | 9 : 7 | 3 2 : 7 | Септимальная большая терция , [3] [5] терция Болена-Пирса, [3] супермажорная терция [14] | 7 | |||
444,77 | Ф↓ | 128 : 99 | 2 7 : 9×11 | 99-я субгармоника [5] [6] | 11 | |||
450.00 | Э /Ф /Ф | 2 9/24 | 2 9/24 | 9 шагов в 24 равномерно темперированных ладах | 24 | |||
450.05 | 83 : 64 | 83 : 2 6 | Восемьдесят третья гармоника [5] | 83 | ||||
454.21 | Ф ♭ | 13 : 10 | 13 : 2×5 | Трёхступенная большая терция или уменьшенная кварта | 13 | |||
456.99 | Е ♯ [2] | 125 : 96 | 5 3 : 2 5 ×3 | Только что увеличенная третья , увеличенная третья [5] | 5 | |||
462.35 | Э  - - | 64 : 49 | 2 6 : 7 2 | 49-я субгармоника [5] [6] | 7 | |||
470,78 | Ф + [2] + [2] | 21 : 16 | 3×7 : 2 4 | Двадцать первая гармоника, узкая кварта, [3] септимальная кварта, [5] широкая увеличенная терция, [ требуется ссылка ] H7 на G | 7 | |||
475.00 | 2 19/48 | 2 19/48 | 19 шагов в 48 равномерно темперированных ладах | 48 | ||||
478.49 | Е ♯ + | 675 : 512 | 3 3 ×5 2 : 2 9 | Шестьсот семьдесят пятая гармоника, широкая увеличенная терция [3] | 5 | |||
480.00 | 2 2/5 | 2 2/5 | 2 шага в 5 равномерно темперированных ладах | 5 | ||||
491.27 | Э ♯ ♯ | 85 : 64 | 5×17 : 2 6 | Восемьдесят пятая гармоника [5] | 17 | |||
498.04 | Ф [2] | 4 : 3 | 2 2 : 3 | Чистая кварта, [3] [5] [16] Пифагорейская совершенная кварта , Просто совершенная кварта или диатессарон [4] | 3 | С | ||
500.00 | Ф | 2 5/12 | 2 5/12 | Равномерно темперированная чистая кварта | 12 | М | ||
501.42 | Ф + + | 171 : 128 | 3 2 ×19 : 2 7 | Сто семьдесят первая гармоника | 19 | |||
510.51 | (3 : 2) 8/11 | 3 8/11 : 2 8/11 | Бета-шкала чистая кварта | 18.75 | ||||
511.52 | Ф | 43 : 32 | 43 : 2 5 | Сорок третья гармоника [5] | 43 | |||
514.29 | 2 3/7 | 2 3/7 | 3 шага в 7 равномерно темперированных ладах | 7 | ||||
519.55 | Ф+ [2] | 27 : 20 | 3 3 : 2 2 ×5 | 5-предельная волчья кварта , острая кварта, [3] несовершенная кварта [16] | 5 | |||
521.51 | Е ♯ +++ | 177147 : 131072 | 3 11 : 2 17 | Пифагорейская увеличенная терция [3] [6] ( F+ (высота тона) ) | 3 | |||
525.00 | 2 7/16 | 2 21/48 | 21 шаг в 48 равномерно темперированных ладах | 16, 48 | ||||
531.53 | Ф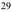 + + | 87 : 64 | 3×29 : 2 6 | Восемьдесят седьмая гармоника [5] | 29 | |||
536.95 | Ф ↓ ♯ + | 15 : 11 | 3×5 : 11 | Недесятичная увеличенная четвертая [3] | 11 | |||
550.00 | Ф /Г /Г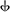 | 2 11/24 | 2 11/24 | 11 шагов в 24 равномерно темперированных ладах | 24 | |||
551.32 | Ф ↑ [2] | 11 : 8 | 11 : 2 3 | одиннадцатая гармоника , [5] недесятичный тритон, [5] малый недесятичный тритон, недесятичный полуувеличенный кварта [3] | 11 | |||
563.38 | Ф ♯ + ♯ + | 18 : 13 | 2×9 : 13 | Тридесятеричная увеличенная четвертая [3] | 13 | |||
568.72 | Ф ♯ [2] | 25 : 18 | 5 2 : 2×3 2 | Только что дополненный четвертый [3] [5] | 5 | |||
570,88 | 89 : 64 | 89 : 2 6 | Восемьдесят девятая гармоника [5] | 89 | ||||
575.00 | 2 23/48 | 2 23/48 | 23 шага в 48 равномерно темперированных ладах | 48 | ||||
582.51 | Г ♭ [2] ♭ [2] | 7 : 5 | 7 : 5 | Малый септимальный тритон , септимальный тритон [3] [4] [5] Тритон Гюйгенса или кварта Болена-Пирса, [3] септимальная квинта, [11] септимальная уменьшенная квинта [19] | 7 | |||
588.27 | Г ♭ −− | 1024 : 729 | 2 10 : 3 6 | Пифагорейская уменьшенная квинта , [3] [6] низкий пифагорейский тритон [5] | 3 | |||
590.22 | Ф ♯ + [2] | 45 : 32 | 3 2 ×5 : 2 5 | Только увеличенная кварта, только тритон, [4] [11] тритон, [6] диатонический тритон, [3] «увеличенная» или «ложная» кварта, [16] тритон с высоким пределом 5, [5] 1 ⁄ 6 - запятая означает одну увеличенную кварту | 5 | |||
595.03 | Г  ♭ ♭ | 361 : 256 | 19 2 : 2 8 | Триста шестьдесят первая гармоника | 19 | |||
600.00 | Ф ♯ /Г ♭ | 2 6/12 | 2 1/2 = √ 2 | Равномерно темперированный тритон | 2, 12 | М | ||
609.35 | Г  ♭ ♭ | 91 : 64 | 7×13 : 2 6 | Девяносто первая гармоника [5] | 13 | |||
609,78 | С ♭ − [2] | 64 : 45 | 2 6 : 3 2 ×5 | Только тритон, [4] 2-й тритон, [6] «ложная» квинта, [16] уменьшенная квинта, [13] тритон нижнего предела 5-й ступени, [5] 45-я субгармоника | 5 | |||
611.73 | Ф ♯ ++ | 729 : 512 | 3 6 : 2 9 | Пифагорейский тритон , [3] [6] Пифагорейский увеличенный кварта, высокий пифагорейский тритон [5] | 3 | |||
617.49 | Ф ♯ [2] [2] | 10 : 7 | 2×5 : 7 | Большой септимальный тритон , септимальный тритон, [4] [5] Тритон Эйлера [3] | 7 | |||
625.00 | 2 25/48 | 2 25/48 | 25 шагов в 48 равномерно темперированных ладах | 48 | ||||
628.27 | Ф ♯ + ♯ + | 23 : 16 | 23 : 2 4 | Двадцать третья гармоника, [5] классическая уменьшенная квинта [ необходима ссылка ] | 23 | |||
631.28 | С ♭ [2] | 36 : 25 | 2 2 ×3 2 : 5 2 | Только что уменьшенная квинта [5] | 5 | |||
646.99 | Ф ♯ + ♯ + | 93 : 64 | 3×31 : 2 6 | Девяносто третья гармоника [5] | 31 | |||
648.68 | Г↓ [2] | 16 : 11 | 2 4 : 11 | ` недесятичная полууменьшенная квинта [3] | 11 | |||
650.00 | Ф /Г /Г | 2 13/24 | 2 13/24 | 13 шагов в 24 равномерно темперированных ладах | 24 | |||
665.51 | Г | 47 : 32 | 47 : 2 5 | Сорок седьмая гармоника [5] | 47 | |||
675.00 | 2 9/16 | 2 27/48 | 27 шагов в 48 равномерно темперированных ладах | 16, 48 | ||||
678.49 | А −−− −−− | 262144 : 177147 | 2 18 : 3 11 | Пифагорейская уменьшенная секста [3] [6] | 3 | |||
680.45 | Г− | 40 : 27 | 2 3 ×5 : 3 3 | 5-предельная волчья квинта , [5] или уменьшенная секста , глухая квинта, [3] [6] [11] несовершенная квинта, [16] | 5 | |||
683.83 | Г | 95 : 64 | 5×19 : 2 6 | Девяносто пятая гармоника [5] | 19 | |||
684.82 | Э    + + + + | 12167 : 8192 | 23 3 : 2 13 | 12167-я гармоника | 23 | |||
685.71 | 2 4/7 : 1 | 4 шага в 7 равномерно темперированных ладах | ||||||
691.20 | 3:2÷(81:80) 1/2 | 2×5 1/2 : 3 | Половина запятой означала одну чистую квинту | М | ||||
694.79 | 3:2÷(81:80) 1/3 | 2 1/3 ×5 1/3 : 3 1/3 | 1 ⁄ 3 - запятая означала одну чистую квинту | М | ||||
695.81 | 3:2÷(81:80) 2/7 | 2 1/7 ×5 2/7 : 3 1/7 | 2 ⁄ 7 - запятая означала одну чистую квинту | М | ||||
696.58 | 3:2÷(81:80) 1/4 | 5 1/4 | Четверть запятой означала одну чистую квинту | М | ||||
697.65 | 3:2÷(81:80) 1/5 | 3 1/5 ×5 1/5 : 2 1/5 | 1 ⁄ 5 - запятая означала одну чистую квинту | М | ||||
698.37 | 3:2÷(81:80) 1/6 | 3 1/3 ×5 1/6 : 2 1/3 | 1 ⁄ 6 - запятая означала одну чистую квинту | М | ||||
700.00 | Г | 2 7/12 | 2 7/12 | Равномерно темперированная чистая квинта | 12 | М | ||
701.89 | 2 31/53 | 2 31/53 | 53-TET чистая квинта | 53 | ||||
701.96 | Г [2] | 3 : 2 | 3 : 2 | Чистая квинта , [3] [5] [16] Пифагорейская чистая квинта, Просто чистая квинта или диапенте , [4] квинта, [14] Просто квинта [11] | 3 | С | ||
702.44 | 2 24/41 | 2 24/41 | 41-TET чистая квинта | 41 | ||||
703.45 | 2 17/29 | 2 17/29 | 29-TET чистая квинта | 29 | ||||
719.90 | 97 : 64 | 97 : 2 6 | Девяносто седьмая гармоника [5] | 97 | ||||
720.00 | 2 3/5 : 1 | 3 шага в 5 равномерно темперированных ладах | 5 | |||||
721.51 | А − − | 1024 : 675 | 2 10 : 3 3 ×5 2 | Узкая уменьшенная секста [3] | 5 | |||
725.00 | 2 29/48 | 2 29/48 | 29 шагов в 48 равномерно темперированных ладах | 48 | ||||
729.22 | Г - - | 32 : 21 | 2 4 : 3×7 | 21-я субгармоника, [5] [6] септимальная уменьшенная шестая | 7 | |||
733.23 | Ф 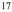  + + | 391 : 256 | 17×23 : 2 8 | Триста девяносто первая гармоника | 23 | |||
737.65 | А  ♭ + ♭ + | 49 : 32 | 7×7 : 2 5 | Сорок девятая гармоника [5] | 7 | |||
743.01 | А | 192 : 125 | 2 6 ×3 : 5 3 | Классическая уменьшенная секста [3] | 5 | |||
750.00 | Г /А /А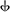 | 2 15/24 | 2 15/24 | 15 шагов в 24 равномерно темперированных ладах | 24 | |||
755.23 | Г ↑ | 99 : 64 | 3 2 ×11 : 2 6 | Девяносто девятая гармоника [5] | 11 | |||
764.92 | А ♭ [2] ♭ [2] | 14 : 9 | 2×7 : 3 2 | Септимальная минорная секста [3] [5] | 7 | |||
772.63 | Г ♯ | 25 : 16 | 5 2 : 2 4 | Только что дополненная пятая [5] [16] | 5 | |||
775.00 | 2 31/48 | 2 31/48 | 31 шаг в 48 равномерно темперированных ладах | 48 | ||||
781.79 | π : 2 | продукт Уоллиса | ||||||
782.49 | Г ↑ - [2] ↑ - [2] | 11 : 7 | 11 : 7 | Недесятичная малая секста , [5] недесятичная увеличенная квинта, [3] числа Фибоначчи | 11 | |||
789.85 | 101 : 64 | 101 : 2 6 | Сто первая гармоника [5] | 101 | ||||
792.18 | А ♭ − [2] | 128 : 81 | 2 7 : 3 4 | Пифагорейская малая секста , [3] [5] [6] 81-я субгармоника | 3 | |||
798.40 | А  ♭ + ♭ + | 203 : 128 | 7×29 : 2 7 | Двести третья гармоника | 29 | |||
800.00 | С ♯ /А ♭ | 2 8/12 | 2 2/3 | Равномерно темперированная малая секста | 3, 12 | М | ||
806.91 | Г ♯ ♯ | 51 : 32 | 3×17 : 2 5 | Пятьдесят первая гармоника [5] | 17 | |||
813.69 | А ♭ [2] | 8 : 5 | 2 3 : 5 | Только малая секста [3] [4] [11] [16] | 5 | |||
815.64 | G ♯ ++ | 6561 : 4096 | 3 8 : 2 12 | Пифагорейская увеличенная квинта , [3] [6] Пифагорейская «схизматическая» секста [5] | 3 | |||
823.80 | 103 : 64 | 103 : 2 6 | Сто третья гармоника [5] | 103 | ||||
825.00 | 2 11/16 | 2 33/48 | 33 шага в 48 равномерно темперированных ладах | 16, 48 | ||||
832.18 | Г ♯ + ♯ + | 207 : 128 | 3 2 ×23 : 2 7 | Двести седьмая гармоника | 23 | |||
833.09 | (5 1/2 +1)/2 | φ : 1 | Золотое сечение ( шкала 833 цента ) | |||||
835.19 | А ♭ + | 81 : 50 | 3 4 : 2×5 2 | Акута минор секста [3] | 5 | |||
840,53 | А ♭ [2] ♭ [2] | 13 : 8 | 13 : 2 3 | Тридецимальная нейтральная секста , [3] обертоновая секста, [5] тринадцатая гармоника | 13 | |||
848.83 | А ♭ ↑ ♭ ↑ | 209 : 128 | 11×19 : 2 7 | Двести девятая гармоника | 19 | |||
850.00 | Г /А /А | 2 17/24 | 2 17/24 | Равномерно темперированная нейтральная секста | 24 | |||
852.59 | А↓+ [2] | 18 : 11 | 2×3 2 : 11 | Нейтральная секста недесятичного типа , [3] [5] Нейтральная секста Залзала | 11 | |||
857.09 | А + + | 105 : 64 | 3×5×7 : 2 6 | Сто пятая гармоника [5] | 7 | |||
857.14 | 2 5/7 | 2 5/7 | 5 шагов в 7 равномерно темперированных строях | 7 | ||||
862.85 | А− | 400 : 243 | 2 4 ×5 2 : 3 5 | Грейв мажор секста [3] | 5 | |||
873.50 | А | 53 : 32 | 53 : 2 5 | Пятьдесят третья гармоника [5] | 53 | |||
875.00 | 2 35/48 | 2 35/48 | 35 шагов в 48 равномерно темперированных ладах | 48 | ||||
879.86 | А↓ | 128 : 77 | 2 7 : 7×11 | 77-я субгармоника [5] [6] | 11 | |||
882.40 | Б −−− −−− | 32768 : 19683 | 2 15 : 3 9 | Пифагорейская уменьшенная септима [3] [6] | 3 | |||
884.36 | А [2] | 5 : 3 | 5 : 3 | Просто большая секста , [3] [4] [5] [11] [16] секста Болена-Пирса, [3] 1 ⁄ 3 - запятая означала одну большую сексту | 5 | М | ||
889.76 | 107 : 64 | 107 : 2 6 | Сто седьмая гармоника [5] | 107 | ||||
892.54 | Б    | 6859 : 4096 | 19 3 : 2 12 | 6859-я гармоника | 19 | |||
900.00 | А | 2 9/12 | 2 3/4 | Равномерно темперированная большая секста | 4, 12 | М | ||
902.49 | А | 32 : 19 | 2 5 : 19 | 19-я субгармоника [5] [6] | 19 | |||
905.87 | А+ [2] | 27 : 16 | 3 3 : 2 4 | Пифагорейский большой секстаккорд [3] [5] [11] [16] | 3 | |||
921.82 | 109 : 64 | 109 : 2 6 | Сто девятая гармоника [5] | 109 | ||||
925.00 | 2 37/48 | 2 37/48 | 37 шагов в 48 равномерно темперированных ладах | 48 | ||||
925.42 | Б − [2] − [2] | 128 : 75 | 2 7 : 3×5 2 | Только что уменьшенная септаккорда , [16] уменьшенная септаккорда, [5] [13] 75-я субгармоника | 5 | |||
925.79 | А  + + | 437 : 256 | 19×23 : 2 8 | Четыреста тридцать седьмая гармоника | 23 | |||
933.13 | А [2] [2] | 12 : 7 | 2 2 ×3 : 7 | Септимальная большая секста [3] [4] [5] | 7 | |||
937.63 | А ↑ | 55 : 32 | 5×11 : 2 5 | Пятьдесят пятая гармоника [5] [20] | 11 | |||
950.00 | А /Б /Б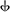 | 2 19/24 | 2 19/24 | 19 шагов в 24 равнотемперированных строях | 24 | |||
953.30 | А ♯ + ♯ + | 111 : 64 | 3×37 : 2 6 | Сто одиннадцатая гармоника [5] | 37 | |||
955.03 | А ♯ [2] | 125 : 72 | 5 3 : 2 3 ×3 2 | Только что дополненный шестой [5] | 5 | |||
957.21 | (3 : 2) 15/11 | 3 15/11 : 2 15/11 | 15 шагов по шкале бета | 18.75 | ||||
960.00 | 2 4/5 | 2 4/5 | 4 шага в 5 равномерно темперированных ладах | 5 | ||||
968.83 | Б ♭ [2] ♭ [2] | 7 : 4 | 7 : 2 2 | Септимальная минорная септима , [4] [5] [11] гармоническая септима, [3] [11] увеличенная секста [ необходима ссылка ] | 7 | |||
975.00 | 2 13/16 | 2 39/48 | 39 шагов в 48 равномерно темперированных ладах | 16, 48 | ||||
976.54 | А ♯ + [2] | 225 : 128 | 3 2 ×5 2 : 2 7 | Только что дополненный шестой [16] | 5 | |||
984.21 | 113 : 64 | 113 : 2 6 | Сто тринадцатая гармоника [5] | 113 | ||||
996.09 | Б ♭ − [2] | 16 : 9 | 2 4 : 3 2 | Пифагорейский малый септаккорд , [3] Малый малый малый септаккорд, [4] Малый малый малый септаккорд, [16] Малый малый септаккорд, [11] Пифагорейский малый малый малый септаккорд [5] | 3 | |||
999.47 | Б ♭ ♭ | 57 : 32 | 3×19 : 2 5 | Пятьдесят седьмая гармоника [5] | 19 | |||
1000.00 | А ♯ /Б ♭ | 2 10/12 | 2 5/6 | Равномерно темперированная малая септаккорда | 6, 12 | М | ||
1014.59 | А ♯ + ♯ + | 115 : 64 | 5×23 : 2 6 | Сто пятнадцатая гармоника [5] | 23 | |||
1017.60 | Б ♭ [2] | 9 : 5 | 3 2 : 5 | Большая малая септаккордовая нота , [16] большая малая септаккордовая нота, [4] [5] септаккорд Болена-Пирса [3] | 5 | |||
1019.55 | А ♯ +++ | 59049 : 32768 | 3 10 : 2 15 | Пифагорейская увеличенная секста [3] [6] | 3 | |||
1025.00 | 2 41/48 | 2 41/48 | 41 шаг в 48 равномерно темперированных ладах | 48 | ||||
1028.57 | 2 6/7 | 2 6/7 | 6 шагов в 7 равномерно темперированных строях | 7 | ||||
1029.58 | Б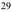 ♭ ♭ | 29 : 16 | 29 : 2 4 | Двадцать девятая гармоника, [5] малая септима [ необходима ссылка ] | 29 | |||
1035.00 | Б↓ [2] | 20 : 11 | 2 2 ×5 : 11 | Малая недесятичная нейтральная септаккорда , большая малая септаккорда [3] | 11 | |||
1039.10 | Б ♭ + | 729 : 400 | 3 6 : 2 4 ×5 2 | Акутовый минорный септаккорд [3] | 5 | |||
1044.44 | Б ♭ ♭ | 117 : 64 | 3 2 ×13 : 2 6 | Сто семнадцатая гармоника [5] | 13 | |||
1044.86 | Б ♭ - ♭ - | 64 : 35 | 2 6 : 5×7 | 35-я субгармоника, [5] септимальная нейтральная септима [6] | 7 | |||
1049.36 | В ↑ ♭ − [2] | 11 : 6 | 11 : 2×3 | 21 ⁄ 4 -тон или недесятичная нейтральная септаккорда , [3] недесятичная «срединная» септаккорда [5] | 11 | |||
1050.00 | А /Б /Б | 2 21/24 | 2 7/8 | Равномерно темперированный нейтральный септаккорд | 8, 24 | |||
1059.17 | 59 : 32 | 59 : 2 5 | Пятьдесят девятая гармоника [5] | 59 | ||||
1066.76 | Б− | 50 : 27 | 2×5 2 : 3 3 | Грейв мажор септаккорд [3] | 5 | |||
1071.70 | Б  ♭ - ♭ - | 13 : 7 | 13 : 7 | Тридесятичный нейтральный септаккорд [21] | 13 | |||
1073.78 | Б 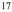 | 119 : 64 | 7×17 : 2 6 | Сто девятнадцатая гармоника [5] | 17 | |||
1075.00 | 2 43/48 | 2 43/48 | 43 шага в 48 равномерно темперированных ладах | 48 | ||||
1086.31 | С′ ♭ −− | 4096 : 2187 | 2 12 : 3 7 | Пифагорейская уменьшенная октава [3] [6] | 3 | |||
1088.27 | Б [2] | 15 : 8 | 3×5 : 2 3 | Только большая септаккорда , [3] [5] [11] [16] малая только большая септаккорда, [4] 1 ⁄ 6 - запятая означает одну большую септаккорду | 5 | |||
1095.04 | С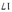 ♭ ♭ | 32 : 17 | 2 5 : 17 | 17-я субгармоника [5] [6] | 17 | |||
1100.00 | Б | 2 11/12 | 2 11/12 | Равномерно темперированный мажорный септаккорд | 12 | М | ||
1102.64 | Б ↑ ↑ ♭ - | 121 : 64 | 11 2 : 2 6 | Сто двадцать первая гармоника [5] | 11 | |||
1107.82 | С′ ♭ − | 256 : 135 | 2 8 : 3 3 ×5 | Октава − мажорная хроматика, [3] 135-я субгармоника, узкая уменьшенная октава [ необходима ссылка ] | 5 | |||
1109.78 | В+ [2] | 243 : 128 | 3 5 : 2 7 | Пифагорейский большой септаккорд [3] [5] [6] [11] | 3 | |||
1116.88 | 61 : 32 | 61 : 2 5 | Шестьдесят первая гармоника [5] | 61 | ||||
1125.00 | 2 15/16 | 2 45/48 | 45 шагов в 48 равномерно темперированных ладах | 16, 48 | ||||
1129.33 | С′ ♭ [2] | 48 : 25 | 2 4 ×3 : 5 2 | Классическая уменьшенная октава, [3] [6] большая только мажорная септаккорда [4] | 5 | |||
1131.02 | Б | 123 : 64 | 3×41 : 2 6 | Сто двадцать третья гармоника [5] | 41 | |||
1137.04 | Б | 27 : 14 | 3 3 : 2×7 | Септимальная большая септима [5] | 7 | |||
1138.04 | С  ♭ ♭ | 247 : 128 | 13×19 : 2 7 | Двести сорок седьмая гармоника | 19 | |||
1145.04 | Б | 31 : 16 | 31 : 2 4 | Тридцать первая гармоника, [5] увеличенная септима [ необходима ссылка ] | 31 | |||
1146.73 | С↓ | 64 : 33 | 2 6 : 3×11 | 33-я субгармоника [6] | 11 | |||
1150.00 | Б /С /С | 2 23/24 | 2 23/24 | 23 шага в 24 равномерно темперированных ладах | 24 | |||
1151.23 | С | 35 : 18 | 5×7 : 2×3 2 | Септимальная супермажорная септима, септимальная четверть тона, обращенная | 7 | |||
1158.94 | В ♯ [2] | 125 : 64 | 5 3 : 2 6 | Только что увеличенная септаккорда , [5] 125-я гармоника | 5 | |||
1172.74 | С + + | 63 : 32 | 3 2 ×7 : 2 5 | Шестьдесят третья гармоника [5] | 7 | |||
1175.00 | 2 47/48 | 2 47/48 | 47 шагов в 48 равномерно темперированных ладах | 48 | ||||
1178.49 | С′− | 160 : 81 | 2 5 ×5 : 3 4 | Октава − синтоническая запятая, [3] полууменьшенная октава [ необходима ссылка ] | 5 | |||
1179,59 | Б ↑ ↑ | 253 : 128 | 11×23 : 2 7 | Двести пятьдесят третья гармоника [5] | 23 | |||
1186.42 | 127 : 64 | 127 : 2 6 | Сто двадцать седьмая гармоника [5] | 127 | ||||
1200.00 | С′ | 2 : 1 | 2 : 1 | Октава [3] [11] или диапазон [4] | 1, 12 | 3 | М | С |
Смотрите также
Примечания
- ^ abcd Обозначение Манери-Симса
Ссылки
- ^ ab Fox, Christopher (2003). «Микротоны и микротональности», Contemporary Music Review , т. 22, ч. 1–2. (Абингдон, Оксфордшир, Великобритания: Routledge): стр. 13.
- ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar as at au av aw ax ay az ba bb bc bd be bf bg bh bi Фонвиль, Джон . 1991. « Расширенная точная интонация Бена Джонстона : руководство для интерпретаторов». Перспективы новой музыки 29, № 2 (лето): 106–137.
- ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar as at au av aw ax ay az ba bb bc bd be bf bg bh bi bj bk bl bm bn bo bp bq br bs bt bu bv bw bx by bz ca cb cc cd ce cf cg ch ci cj ck cl cm cn co cp cq cr cs ct cu cv cw cx cy cz da db dc dd de df dg dh di "Список интервалов", Фонд Гюйгенса-Фоккера . Фонд использует "classic" для обозначения "just" или опускает любое прилагательное, как в "major sext".
- ^ abcdefghijklmnopqrstu vwx Партч, Гарри (1979). Генезис музыки . С. 68–69. ISBN 978-0-306-80106-8.
- ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar as at au av aw ax ay az ba bb bc bd be bf bg bh bi bj bk bl bm bn bo bp bq br bs bt bu bv bw bx by bz ca cb cc cd ce cf cg ch ci cj ck cl cm cn co cp cq cr cs ct cu cv cw cx cy cz da db dc dd de df dg dh di dj dk dl dm dn do dp dq dr ds dt du dv dw dx dy dz «Анатомия октавы», Кайл Ганн (1998). Ганн исключает «just», но включает «5-limit». Он использует «median» вместо «neutral».
- ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar as at au av aw ax ay Haluška, Ян (2003). Математическая теория тональных систем , стр. xxv – xxix. ISBN 978-0-8247-4714-5 .
- ^ Эллис, Александр Дж.; Хипкинс , Альфред Дж. (1884). «Тонометрические наблюдения над некоторыми существующими негармоническими музыкальными гаммами». Труды Лондонского королевского общества . 37 (232–234): 368–385. doi : 10.1098/rspl.1884.0041 . JSTOR 114325. S2CID 122407786.
- ^ "Логарифмические интервальные меры", Фонд Гюйгенса-Фоккера . Доступ 2015-06-06.
- ^ «Темпераменты Оруэлла», Xenharmony.org .
- ^ ab Partch 1979, стр. 70
- ^ abcdefghijklmnopqrstu vwxyz aa ab Александр Джон Эллис (март 1885 г.). О музыкальных гаммах разных народов , стр. 488. Журнал Общества искусств , т. XXXII, № 1688
- ^ Уильям Смайт Бэбкок Мэтьюз (1895). Словарь произношения и краткая энциклопедия музыкальных терминов , стр. 13. ISBN 1-112-44188-3 .
- ^ abcdef Anger, Joseph Humfrey (1912). Трактат о гармонии с упражнениями, том 3 , стр. xiv–xv. W. Tyrrell.
- ^ abcdefghijklmno Герман Людвиг Ф. фон Гельмгольц ( перевод Александра Джона Эллиса ) (1875). «Дополнения переводчика», О ощущениях тона как физиологической основе теории музыки, стр. 644. [ISBN не указан]
- ^ AR Meuss (2004). Интервалы, гаммы, тоны и концертная высота тона C. Temple Lodge Publishing. стр. 15. ISBN 1902636465.
- ^ abcdefghijklmnopqrstu vwxy Пол, Оскар (1885). Руководство по гармонии для использования в музыкальных школах и семинариях, а также для самостоятельного обучения , стр. 165. Теодор Бейкер, перевод Г. Ширмера. Пол использует «natural» вместо «just».
- ^ ab "13-я гармоника", 31et.com .
- ^ Брабнер, Джон ХФ (1884). Национальная энциклопедия , т. 13, стр. 182. Лондон. [ISBN не указан]
- ^ Сабат, Марк и фон Швайниц, Вольфганг (2004). «Расширенная нотация высоты тона Гельмгольца-Эллиса JI» [PDF], NewMusicBox . Доступ: 15 марта 2014 г.
- ^ Герман Л. Ф. фон Гельмгольц (2007). Ощущения тона , стр. 456. ISBN 978-1-60206-639-7 .
- ^ «Галерея справедливых интервалов», Xenharmonic Wiki .
Внешние ссылки
- «Имена семипредельных запятых», XenHarmony.org . (Архивная копия)
- «Список обертонов», Xenharmonic Wiki .
- «Все известные музыкальные интервалы» (Дэйл Понд), Svpvril.com.