72 равномерно темперированный
В музыке 72 равномерная темперация , называемая двенадцатитоновой , 72 TET , 72 EDO или 72 ET , — это темперированная гамма, полученная путем деления октавы на двенадцатые тона, или, другими словами, 72 равных шага (равные частотные отношения). ⓘ Каждый шаг представляет собой частотное отношение 72 √ 2 или 16 + 2 /3 центов , который делит 100 центов 12 EDO « полутон » на 6 равных частей (100 центов ÷ 16 + 2 /3 = 6 шагов, ровно) и, таким образом, является «двенадцатым тоном» (ⓘ ). Поскольку 72 делится на 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72, 72 EDO включает в себя все эти равнотемперированные строи. Поскольку он содержит так много темпераций, 72 EDO содержит в то же время темперированные полутоны, терции, четверти и сексты, что делает его очень универсальным строем.
Это разделение октавы привлекло большое внимание теоретиков настройки, поскольку, с одной стороны, оно подразделяет стандартную 12 равномерно темперированную тональность , а с другой стороны, оно точно представляет обертоны до двенадцатого парциального тона, и, следовательно, может использоваться для музыки в 11-м пределе . Оно было теоретически обосновано в форме двенадцатых тонов Алоисом Хабой [1] и Иваном Вышнеградским [2] [ 3] [4], которые считали его хорошим подходом к континууму звука. 72 EDO также упоминается среди разделений тона Хулианом Каррильо , который предпочитал шестнадцатый тон (96 EDO) как приближение к непрерывному звуку в прерывистых гаммах.
История и использование
византийская музыка
Равномерная темперация 72 используется в византийской музыкальной теории [5], разделяя октаву на 72 равных мории , что само по себе происходит от интерпретаций теорий Аристоксена , который использовал нечто похожее. Хотя равномерная темперация 72 основана на иррациональных интервалах (см. выше), как и равномерная темперация 12 тонов (12 EDO), в основном используемая в западной музыке (и которая содержится как подмножество в равномерная темперация 72), равномерная темперация 72, как гораздо более тонкое деление октавы, является превосходной настройкой как для представления деления октавы в соответствии с древнегреческой диатоникой , так и хроматическими родами , в которых интервалы основаны на соотношениях между нотами, и для представления с большой точностью многих рациональных интервалов, а также иррациональных интервалов.
Другая история и использование
Ряд композиторов использовали его, и они представляют совершенно разные точки зрения и типы музыкальной практики. Среди них Алоис Хаба , Хулиан Каррильо, Иван Вышнеградский и Яннис Ксенакис . [ необходима цитата ]
Многие другие композиторы используют его свободно и интуитивно, например, джазовый музыкант Джо Манери , и композиторы, ориентированные на классику, например, Джулия Вернц и другие, связанные с Бостонским микротональным обществом . Другие, например, нью-йоркский композитор Джозеф Персон, интересуются им, потому что он поддерживает использование чудесной темперации , а третьи просто потому, что он приближается к более высокому пределу просто интонации, например, Эзра Симс и Джеймс Тенни . Также существовала активная советская школа из 72 композиторов EDO с менее известными именами: Евгений Александрович Мурзин, Андрей Волконский , Николай Никольский , Эдуард Артемьев , Александр Немтин, Андрей Эшпай , Геннадий Гладков , Петр Мещанинов и Станислав Крейчи. [ требуется ссылка ]
Синтезатор ANS использует 72 равномерно темперированных строя.
Обозначение
Система обозначений Манери-Симса, разработанная для 72 EDO, использует знаки альтерации ↓ и ↑ для 1/ 12 тонвниз и вверх (1 шаг= 16 + 2 /3 центов),  и
и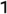 для 1 /6 внизи вверх (2 шага= 33 + 1 /3 центов), и
для 1 /6 внизи вверх (2 шага= 33 + 1 /3 центов), и и
и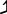 для семеричного 1 /4 вверх и вниз (3 шага= 50 центов = половина 12 EDO диез).
для семеричного 1 /4 вверх и вниз (3 шага= 50 центов = половина 12 EDO диез).
Их можно комбинировать с традиционными символами диеза и бемоля (6 шагов = 100 центов), помещая перед ними, например: ♭ или
♭ или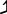 ♭ , но без промежуточного пробела. A 1 /3 тон может быть одним из следующих ↑
♭ , но без промежуточного пробела. A 1 /3 тон может быть одним из следующих ↑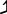 , ↓
, ↓ ,
, ♯ , или
♯ , или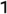 ♭ (4 шага = 66 + 2 /3 ) в то время как 5 шагов могут быть
♭ (4 шага = 66 + 2 /3 ) в то время как 5 шагов могут быть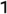
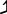 , ↓ ♯ или ↑ ♭ ( 83 + 1 /3 центов).
, ↓ ♯ или ↑ ♭ ( 83 + 1 /3 центов).
Размер интервала

Ниже приведены размеры некоторых интервалов (обычных и эзотерических) в этой настройке. Для справки, различия менее 5 центов мелодически незаметны для большинства людей и приближаются к пределам возможной точности настройки для акустических инструментов. Обратите внимание, что невозможно, чтобы любой тон был дальше 8 + 1 /3 центов от ближайшей купюры достоинством 72 EDO, поскольку размер шага между ними составляет 16 + 2 /3 центов. Поэтому для сравнения, ошибки высоты тона около 8 центов (для этой тонкой настройки) плохо соответствуют, тогда как практический предел для настройки любого акустического инструмента составляет в лучшем случае около 2 центов, что было бы очень хорошим соответствием в таблице — это применимо даже к электронным инструментам, если они производят ноты, которые показывают какие-либо слышимые следы вибрато . [ требуется цитата ]
| Название интервала | Размер (шаги) | Размер ( центы ) | MIDI- аудио | Просто соотношение | Всего ( центов ) | MIDI- аудио | Ошибка |
|---|---|---|---|---|---|---|---|
| октава | 72 | 1200 | 2:1 | 1200 | 0 | ||
| гармонический септаккорд | 58 | 966.67 | 7:4 | 968.83 | −2,16 | ||
| чистая квинта | 42 | 700 | ⓘ | 3:2 | 701.96 | ⓘ | −1,96 |
| семнадцатеричный тритон | 36 | 600 | ⓘ | 17:12 | 603.00 | −3.00 | |
| септальный тритон | 35 | 583.33 | ⓘ | 7:5 | 582.51 | ⓘ | +0,82 |
| тридецимальный тритон | 34 | 566.67 | ⓘ | 18:13 | 563.38 | +3.28 | |
| 11-я гармоника | 33 | 550 | ⓘ | 11:8 | 551.32 | ⓘ | −1,32 |
| (15:11) увеличенная четвертая | 32 | 533.33 | ⓘ | 15:11 | 536.95 | ⓘ | −3,62 |
| идеальная четвертая | 30 | 500 | ⓘ | 4:3 | 498.04 | ⓘ | +1.96 |
| септимальная узкая кварта | 28 | 466.66 | ⓘ | 21:16 | 470,78 | ⓘ | −4,11 |
| 17:13 узкая четвертая | 17:13 | 464.43 | +2.24 | ||||
| трехзначная большая терция | 27 | 450 | ⓘ | 13:10 | 454.21 | ⓘ | −4,21 |
| септендециальная супербольшая терция | 22:17 | 446.36 | +3.64 | ||||
| септимальная большая терция | 26 | 433.33 | ⓘ | 9:7 | 435.08 | ⓘ | −1,75 |
| недесятичная большая терция | 25 | 416.67 | ⓘ | 14:11 | 417.51 | ⓘ | −0,84 |
| квазитемперированная большая терция | 24 | 400 | ⓘ | 5:4 | 386.31 | ⓘ | 13.69 |
| большая терция | 23 | 383.33 | ⓘ | 5:4 | 386.31 | ⓘ | −2,98 |
| тридецимальная нейтральная третья | 22 | 366.67 | ⓘ | 16:13 | 359.47 | +7.19 | |
| нейтральный третий | 21 | 350 | ⓘ | 11:9 | 347.41 | ⓘ | +2.59 |
| семеричная верхняя треть | 20 | 333.33 | ⓘ | 17:14 | 336.13 | −2,80 | |
| малая терция | 19 | 316.67 | ⓘ | 6:5 | 315.64 | ⓘ | +1.03 |
| квазитемперированная малая терция | 18 | 300 | ⓘ | 25:21 | 301.85 | −1,85 | |
| тридесятичная малая терция | 17 | 283.33 | ⓘ | 13:11 | 289.21 | ⓘ | −5,88 |
| септимальная малая терция | 16 | 266.67 | ⓘ | 7:6 | 266.87 | ⓘ | −0,20 |
| тридецимальная 5 /4 тон | 15 | 250 | ⓘ | 15:13 | 247.74 | +2.26 | |
| септальный целый тон | 14 | 233.33 | ⓘ | 8:7 | 231.17 | ⓘ | +2.16 |
| семнадцатеричный целый тон | 13 | 216.67 | ⓘ | 17:15 | 216.69 | −0,02 | |
| целый тон , мажорный тон | 12 | 200 | ⓘ | 9:8 | 203.91 | ⓘ | −3,91 |
| целый тон , минорный тон | 11 | 183.33 | ⓘ | 10:9 | 182.40 | ⓘ | +0,93 |
| большая недесятичная нейтральная секунда | 10 | 166.67 | ⓘ | 11:10 | 165.00 | ⓘ | +1.66 |
| меньшая недесятичная нейтральная секунда | 9 | 150 | ⓘ | 12:11 | 150,64 | ⓘ | −0,64 |
| большая трехдесятичная 2 /3 тон | 8 | 133.33 | ⓘ | 13:12 | 138,57 | ⓘ | −5,24 |
| великая лимма | 27:25 | 133.24 | ⓘ | +0,09 | |||
| меньшая трехдесятичная 2/3 тон | 14:13 | 128.30 | ⓘ | +5.04 | |||
| септальный диатонический полутон | 7 | 116.67 | ⓘ | 15:14 | 119.44 | ⓘ | −2,78 |
| диатонический полутон | 16:15 | 111.73 | ⓘ | +4.94 | |||
| большой семнадцатеричный полутон | 6 | 100 | ⓘ | 17:16 | 104.95 | ⓘ | −4,95 |
| малый септендецимальный полутон | 18:17 | 98.95 | ⓘ | +1.05 | |||
| семеричный хроматический полутон | 5 | 83.33 | ⓘ | 21:20 | 84.47 | ⓘ | −1,13 |
| хроматический полутон | 4 | 66.67 | ⓘ | 25:24 | 70,67 | ⓘ | −4,01 |
| септимальный третий тон | 28:27 | 62.96 | ⓘ | +3.71 | |||
| септимальная четверть тона | 3 | 50 | ⓘ | 36:35 | 48.77 | ⓘ | +1.23 |
| семеричный диезис | 2 | 33.33 | ⓘ | 49:48 | 35.70 | ⓘ | −2,36 |
| недесятичная запятая | 1 | 16.67 | ⓘ | 100:99 | 17.40 | −0,73 |
Хотя 12 EDO можно рассматривать как подмножество 72 EDO, ближайшие соответствия наиболее часто используемым интервалам под 72 EDO отличаются от ближайших соответствий под 12 EDO. Например, большая терция 12 EDO, которая является диезом, существует как интервал из 24 шагов в 72 EDO, но интервал из 23 шагов гораздо ближе к соотношению 5:4 только большой терции.
12 EDO имеет очень хорошее приближение для чистой квинты (третьей гармоники), особенно для такого небольшого количества шагов на октаву, но по сравнению с одинаково темперированными версиями в 12 EDO, только мажорная терция (пятая гармоника) смещена примерно на одну шестую шага, седьмая гармоника смещена примерно на треть шага, а одиннадцатая гармоника смещена примерно на половину шага. Это говорит о том, что если бы каждый шаг 12 EDO был разделен на шесть, пятая, седьмая и одиннадцатая гармоники теперь были бы хорошо аппроксимированы, в то время как превосходное приближение третьей гармоники 12 EDO было бы сохранено. Действительно, все интервалы, включающие гармоники вплоть до 11-й, очень близко совпадают в 72 EDO; никакие интервалы, образованные как разница любых двух из этих интервалов, не темперируются этой системой настройки. Таким образом, 72 EDO можно рассматривать как предлагающее почти идеальное приближение к музыке предела 7, 9 и 11 . Что касается высших гармоник, то ряд интервалов все еще достаточно хорошо согласованы, но некоторые из них темперированы. Например, комма 169:168 темперирована, но другие интервалы, включающие 13-ю гармонику, выделяются.
В отличие от таких строев, как 31 EDO и 41 EDO , 72 EDO содержит много интервалов, которые не соответствуют ни одной малой (< 16) гармонике в гармоническом ряду.
Масштабная диаграмма

Поскольку 72 EDO содержит 12 EDO, масштаб 12 EDO находится в 72 EDO. Однако истинный масштаб может быть лучше аппроксимирован другими интервалами.
Смотрите также
Ссылки
- ^ Хаба, А. (1978) [1927]. Harmonicé základy ctvrttónové soustavy [ Немецкий перевод Neue Harmonielehre des Diatonischen, chromatischen Viertel-, Drittel-, Sechstel- und Zwölftel-tonsystems Английский перевод Гармонические основы четвертьтоновой системы ] (на чешском и немецком языках). Перевод Кистнера, о. Лейпциг (1927) / Вена, 1978: CFW Сигел (1927) / Универсал (1978).
{{cite book}}: CS1 maint: местоположение ( ссылка )- Пересмотренное немецкое издание:
- ^ Вышнеградский, И. (1972). «Ультрахроматизм и пространства, не октавианты». Музыкальное ревю ( 290–291 ): 71–141 .
- ^ Енджеевски, Франк, изд. (1996) [1953]. La Loi de la Pansonorité [ Законы многотональной музыки ] (рукопись) (на французском языке). Критон, Паскаль (предисловие). Женева, Швейцария: Ред. Контрешам. ISBN 978-2-940068-09-8.
- ^ Енджеевски, Франк, изд. (2005) [1936]. Une philosophie dialectique de l'art music [ Диалектическая философия музыкального искусства ] (рукопись) (на французском языке). Париж, Франция: Ред. Л'Харматтан. ISBN 978-2-7475-8578-1.
- ^ Chryssochoidis, G.; Delviniotis, D.; Kouroupetroglou, G. (11–13 июля 2007 г.). «Полуавтоматическая методология тегирования для акустических корпусов православных церковных песнопений» (PDF) . Труды SMC'07 . 4-я конференция по звуковым и музыкальным вычислениям. Лефкада, Греция. Архивировано (PDF) из оригинала 15 августа 2007 г. . Получено 24 апреля 2008 г. .
Внешние ссылки
- "Бостонское микротональное общество" (официальный сайт). Архивировано из оригинала 2011-02-09 . Получено 2005-12-05 – через bostonmicrotonalsociety.org.
- "Нотация Вышнеградского для двенадцатого тона". Архивировано из оригинала 4 апреля 2023 г. Получено 24 июня 2022 г. – через sagittal.org.
- «Sagittal» (главная страница сайта) – через sagittal.org.
- "Sagittal notation". The Xenharmonic wiki . Архивировано из оригинала 2022-10-22 . Получено 2022-06-24 – через en.xen.wiki.
- «Изменения». Ekmelic Music. 27 сентября 2017 г. Архивировано из оригинала 4 октября 2017 г. Получено 16 октября 2017 г. – через ekmelic-music.org.— символы для нотации Манери-Симса и другие
- Спиракис, Иоаннис. "Η Η Ελληνική Σελίδα για τη Βυζαντινή Μουσική» [Византийская музыка, электроакустическая музыка, музыковедение, образование] (на греческом и английском языках). Архивировано из оригинала 5 апреля 2023 года . Проверено 19 ноября 2024 г. - через g-cultural.org.