Полиномиальный
В математике многочлен — это математическое выражение , состоящее из неопределенных (также называемых переменными ) и коэффициентов , которое включает только операции сложения , вычитания , умножения и возведения в степень с неотрицательными целыми степенями и имеет конечное число членов. [1] [2] [3] [4] [5] Примером многочлена с одним неопределенным x является x 2 − 4 x + 7. Примером с тремя неизвестными является x 3 + 2 xyz 2 − yz + 1 .
Полиномы появляются во многих областях математики и науки. Например, они используются для формирования полиномиальных уравнений , которые кодируют широкий спектр проблем, от элементарных текстовых задач до сложных научных проблем; они используются для определения полиномиальных функций , которые появляются в различных условиях, от базовой химии и физики до экономики и социальных наук ; и они используются в исчислении и численном анализе для аппроксимации других функций. В высшей математике полиномы используются для построения полиномиальных колец и алгебраических многообразий , которые являются центральными понятиями в алгебре и алгебраической геометрии .
Этимология
Слово полином объединяет два разных корня : греческое poly , означающее «много», и латинское nomen , или «имя». Оно произошло от термина биномиальный путем замены латинского корня bi- на греческое poly- . То есть, оно означает сумму многих членов (многих одночленов ). Слово полиномиальный впервые было использовано в 17 веке. [6]
Обозначения и терминология

X, встречающийся в полиноме, обычно называется переменной или неопределенностью . Когда полином рассматривается как выражение, x является фиксированным символом, который не имеет никакого значения (его значение «неопределенность»). Однако, когда рассматривается функция, определяемая полиномом, то x представляет собой аргумент функции и поэтому называется «переменной». Многие авторы используют эти два слова как взаимозаменяемые.
Полином P от неопределенного x обычно обозначается либо как P , либо как P ( x ). Формально имя полинома — P , а не P ( x ), но использование функциональной нотации P ( x ) восходит к тому времени, когда различие между полиномом и связанной функцией было неясным. Более того, функциональная нотация часто полезна для указания в одной фразе полинома и его неопределенного. Например, «пусть P ( x ) будет полиномом» является сокращением для «пусть P будет полиномом от неопределенного x ». С другой стороны, когда нет необходимости подчеркивать имя неопределенного, многие формулы намного проще и легче читать, если имя(и) неопределенного(ых) не появляются при каждом появлении полинома.
Неоднозначность наличия двух обозначений для одного математического объекта может быть формально разрешена путем рассмотрения общего значения функциональной нотации для полиномов. Если a обозначает число, переменную, другой полином или, в более общем смысле, любое выражение, то P ( a ) обозначает, по соглашению, результат подстановки a вместо x в P . Таким образом, полином P определяет функцию , которая является полиномиальной функцией, связанной с P . Часто при использовании этой нотации предполагается, что a — число. Однако ее можно использовать в любой области, где определены сложение и умножение (то есть в любом кольце ). В частности, если a — полином, то P ( a ) также является полиномом.
Более конкретно, когда a — неопределенность x , то изображение x этой функцией — это сам многочлен P (подстановка x вместо x ничего не меняет). Другими словами, что формально оправдывает существование двух обозначений для одного и того же многочлена .
Определение
Полиномиальное выражение — это выражение , которое может быть построено из констант и символов, называемых переменными или неопределенными, с помощью сложения , умножения и возведения в степень неотрицательного целого числа . Константы обычно являются числами , но могут быть любым выражением, которое не включает неопределенные и представляет собой математические объекты , которые можно складывать и умножать. Два полиномиальных выражения считаются определяющими один и тот же полином, если их можно преобразовать одно в другое, применяя обычные свойства коммутативности , ассоциативности и дистрибутивности сложения и умножения. Например, и — это два полиномиальных выражения, которые представляют один и тот же полином; поэтому одно из них имеет равенство .
Многочлен от одного неопределенного x всегда можно записать (или переписать) в виде , где — константы, называемые коэффициентами многочлена, а — неопределенное. [7] Слово «неопределенное» означает, что не представляет никакого конкретного значения, хотя вместо него может быть подставлено любое значение. Отображение, которое связывает результат этой подстановки с подставленным значением, — это функция , называемая полиномиальной функцией .
Это можно выразить более кратко, используя запись суммирования : То есть, многочлен может быть либо равен нулю, либо может быть записан в виде суммы конечного числа ненулевых членов . Каждый член состоит из произведения числа, называемого коэффициентом члена [a] , и конечного числа неопределенных, возведенных в неотрицательные целые степени.
Классификация
Степень неопределенности в члене называется степенью этой неопределенности в этом члене; степень члена — это сумма степеней неопределенностей в этом члене, а степень многочлена — это наибольшая степень любого члена с ненулевым коэффициентом. [8] Поскольку x = x 1 , степень неопределенности без записанной степени равна единице.
Член без неизвестных и многочлен без неизвестных называются, соответственно, постоянным членом и постоянным многочленом . [b] Степень постоянного члена и ненулевого постоянного многочлена равна 0. Степень нулевого многочлена 0 (который вообще не имеет членов) обычно рассматривается как неопределенная (но см. ниже). [9]
Например: — термин. Коэффициент равен −5 , неопределенные — x и y , степень x равна двум, а степень y равна единице. Степень всего термина равна сумме степеней каждого неопределенного в нем, поэтому в этом примере степень равна 2 + 1 = 3 .
Формирование суммы нескольких членов дает многочлен. Например, следующий пример — многочлен: Он состоит из трех членов: первый — второй степени, второй — первой степени, а третий — нулевой степени.
Многочлены малой степени получили специальные названия. Многочлен нулевой степени — это постоянный многочлен или просто константа . Многочлены первой, второй или третьей степени — это соответственно линейные многочлены, квадратные многочлены и кубические многочлены . [8] Для более высоких степеней специальные названия обычно не используются, хотя иногда используются многочлен четвертой степени (для степени четыре) и многочлен пятой степени (для степени пять). Названия степеней могут применяться к многочлену или к его членам. Например, член 2 x в x 2 + 2 x + 1 является линейным членом в квадратном многочлене.
Многочлен 0, который можно считать вообще не имеющим членов, называется нулевым многочленом . В отличие от других постоянных многочленов, его степень не равна нулю. Вместо этого степень нулевого многочлена либо остается явно неопределенной, либо определяется как отрицательная (либо −1, либо −∞). [10] Нулевой многочлен также уникален тем, что это единственный многочлен от одной неизвестной, который имеет бесконечное число корней . Графиком нулевого многочлена, f ( x ) = 0 , является ось x .
В случае полиномов от более чем одной неизвестной полином называется однородным степени n , если все его ненулевые члены имеют степень n . Нулевой полином является однородным, и, как однородный полином, его степень не определена. [c] Например, x 3 y 2 + 7 x 2 y 3 − 3 x 5 является однородным степени 5. Подробнее см. Однородный полином .
Коммутативный закон сложения может быть использован для перестановки членов в любом предпочтительном порядке. В многочленах с одним неизвестным члены обычно упорядочены в соответствии со степенью, либо в «убывающем порядке степеней x », с членом наибольшей степени первым, либо в «возрастающем порядке степеней x ». Многочлен 3 x 2 − 5 x + 4 записан в порядке убывания степеней x . Первый член имеет коэффициент 3 , неопределенный x и показатель 2. Во втором члене коэффициент равен −5 . Третий член является константой. Поскольку степень ненулевого многочлена является наибольшей степенью любого одного члена, этот многочлен имеет степень два. [11]
Два члена с одинаковыми неопределенными, возведенными в одинаковые степени, называются «подобными членами» или «подобными членами», и их можно объединить, используя распределительный закон , в один член, коэффициент которого является суммой коэффициентов членов, которые были объединены. Может случиться, что это сделает коэффициент равным 0. [12] Многочлены можно классифицировать по количеству членов с ненулевыми коэффициентами, так что одночленный многочлен называется мономом , [ d] двухчленный многочлен называется биномом , а трехчленный многочлен называется триномом .
Действительный многочлен — это многочлен с действительными коэффициентами. Когда он используется для определения функции , область определения не так ограничена. Однако, функция действительного многочлена — это функция от действительных чисел до действительных чисел, которая определяется действительным многочленом. Аналогично, целочисленный многочлен — это многочлен с целыми коэффициентами, а комплексный многочлен — это многочлен с комплексными коэффициентами.
Многочлен от одной неизвестной называется одномерным многочленом , многочлен от более чем одной неизвестной называется многомерным многочленом . Многочлен с двумя неизвестными называется двумерным многочленом . [7] Эти понятия больше относятся к виду многочленов, с которыми обычно работают, чем к отдельным многочленам; например, при работе с одномерными многочленами не исключаются постоянные многочлены (которые могут быть результатом вычитания непостоянных многочленов), хотя, строго говоря, постоянные многочлены вообще не содержат никаких неизвестных. Можно далее классифицировать многомерные многочлены как двумерные , трехмерные и так далее, в соответствии с максимально допустимым числом неизвестных. Опять же, для того чтобы рассматриваемое множество объектов было замкнуто относительно вычитания, изучение трехмерных многочленов обычно допускает двумерные многочлены и так далее. Также принято говорить просто «многочлены от x , y и z », перечисляя допустимые неопределенности.
Операции
Сложение и вычитание
Многочлены можно складывать, используя ассоциативный закон сложения (группируя все их члены в одну сумму), возможно, с последующим переупорядочением (используя коммутативный закон ) и объединением подобных членов. [12] [13] Например, если и , то сумму можно переупорядочить и перегруппировать как , а затем упростить до Когда многочлены складываются, результатом является другой многочлен. [14]
Вычитание многочленов выполняется аналогично.
Умножение
Многочлены также можно умножать. Чтобы разложить произведение двух многочленов в сумму членов, многократно применяется распределительный закон, в результате чего каждый член одного многочлена умножается на каждый член другого. [12] Например, если тогда Выполнение умножения в каждом члене дает Объединение подобных членов дает что можно упростить до Как в примере, произведение многочленов всегда является многочленом. [14] [9]
Состав
Если задан полином одной переменной и другой полином g любого числа переменных, композиция получается путем замены каждой копии переменной первого полинома вторым полиномом. [9] Например, если и тогда Композиция может быть расширена до суммы членов с использованием правил умножения и деления полиномов. Композиция двух полиномов является другим полиномом. [15]
Разделение
Деление одного многочлена на другой обычно не является многочленом. Вместо этого такие отношения представляют собой более общее семейство объектов, называемых рациональными дробями , рациональными выражениями или рациональными функциями , в зависимости от контекста. [16] Это аналогично тому, что отношение двух целых чисел является рациональным числом , не обязательно целым числом. [17] [18] Например, дробь 1/( x 2 + 1) не является многочленом, и ее нельзя записать в виде конечной суммы степеней переменной x .
Для многочленов от одной переменной существует понятие евклидова деления многочленов , обобщающее евклидово деление целых чисел. [e] Это понятие деления a ( x )/ b ( x ) приводит к двум многочленам, частному q ( x ) и остатку r ( x ) , таким образом, что a = b q + r и degree( r ) < degree( b ) . Частное и остаток могут быть вычислены любым из нескольких алгоритмов, включая полиномиальное длинное деление и синтетическое деление . [19]
Когда знаменатель b ( x ) является моническим и линейным, то есть b ( x ) = x − c для некоторой константы c , то теорема о полиномиальных остатках утверждает, что остаток от деления a ( x ) на b ( x ) является оценкой a ( c ) . [18] В этом случае частное может быть вычислено по правилу Руффини , частному случаю синтетического деления. [20]
Факторинг
Все многочлены с коэффициентами в уникальной факторизационной области (например, целые числа или поле ) также имеют факторизованную форму, в которой многочлен записывается как произведение неприводимых многочленов и константы. Эта факторизованная форма единственна с точностью до порядка множителей и их умножения на обратимую константу. В случае поля комплексных чисел неприводимые множители линейны. Над действительными числами они имеют степень один или два. Над целыми и рациональными числами неприводимые множители могут иметь любую степень. [21] Например, факторизованная форма есть над целыми и действительными числами, а также над комплексными числами.
Вычисление факторизованной формы, называемое факторизацией , в общем случае слишком сложно для выполнения вручную. Однако эффективные алгоритмы полиномиальной факторизации доступны в большинстве систем компьютерной алгебры .
Исчисление
Вычисление производных и интегралов многочленов особенно просто по сравнению с другими видами функций. Производная многочлена по x — это многочлен Аналогично, общая первообразная (или неопределенный интеграл) от — это где c — произвольная константа. Например, первообразные от x 2 + 1 имеют вид 1/3 х 3 + х + с .
Для многочленов, коэффициенты которых берутся из более абстрактных установок (например, если коэффициенты являются целыми числами по модулю некоторого простого числа p или элементами произвольного кольца), формулу для производной все еще можно интерпретировать формально, при этом коэффициент ka k понимается как сумма k копий a k . Например, по целым числам по модулю p производная многочлена x p + x является многочленом 1 . [22]
Полиномиальные функции
Полиномиальная функция — это функция, которая может быть определена путем вычисления полинома. Точнее, функция f одного аргумента из заданной области является полиномиальной функцией, если существует полином, который вычисляется как для всех x в области определения f (здесь n — неотрицательное целое число, а a 0 , a 1 , a 2 , ..., a n — постоянные коэффициенты). [23] Как правило, если не указано иное, полиномиальные функции имеют комплексные коэффициенты, аргументы и значения. В частности, полином, ограниченный действительными коэффициентами, определяет функцию от комплексных чисел до комплексных чисел. Если область определения этой функции также ограничена действительными числами, результирующая функция является действительной функцией, которая отображает действительные числа в действительные числа.
Например, функция f , определяемая как является полиномиальной функцией одной переменной. Полиномиальные функции нескольких переменных определяются аналогично, используя полиномы от более чем одной неизвестной, как в Согласно определению полиномиальных функций, могут быть выражения, которые, очевидно, не являются полиномами, но тем не менее определяют полиномиальные функции. Примером является выражение , которое принимает те же значения, что и полином на интервале , и, таким образом, оба выражения определяют одну и ту же полиномиальную функцию на этом интервале.
Каждая полиномиальная функция является непрерывной , гладкой и целой .
Оценка многочлена — это вычисление соответствующей полиномиальной функции; то есть оценка состоит из подстановки числового значения вместо каждой неопределенной величины и выполнения указанных умножений и сложений .
Для многочленов с одним неизвестным оценка обычно более эффективна (требуется меньшее количество арифметических операций) с использованием метода Горнера , который заключается в переписывании многочлена в виде
Графики
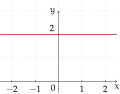
- Многочлен степени 0:
f ( x ) = 2 - Многочлен степени 1:
f ( x ) = 2 x + 1 - Многочлен степени 2:
f ( x ) = x 2 − x − 2
= ( x + 1)( x − 2) - Многочлен степени 3:
f ( x ) = x 3 /4 + 3 x 2 /4 − 3 x /2 − 2
= 1/4 ( x + 4)( x + 1)( x − 2) - Многочлен 4-й степени:
f ( x ) = 1/14 ( x + 4)( x + 1)( x − 1)( x − 3)
+ 0,5 - Многочлен 5-й степени:
f ( x ) = 1/20 ( x + 4)( x + 2)( x + 1)( x − 1)
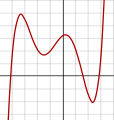
( x − 3) + 2 - Многочлен 6-й степени:
f ( x ) = 1/100 ( x 6 − 2 x 5 − 26 x 4 + 28 x 3
+ 145 x 2 − 26 x − 80) - Многочлен 7-й степени:
f ( x ) = ( x − 3)( x − 2)( x − 1)( x )( x + 1)( x + 2)
( x + 3)
Полиномиальную функцию от одной действительной переменной можно представить в виде графика .
- График нулевого полиномаf ( х ) = 0это ось x .
- График полинома степени 0f ( x ) = a 0 , где a 0 ≠ 0 ,представляет собой горизонтальную линию с точкой пересечения оси Y в точке 0
- График полинома 1-й степени (или линейной функции)f ( x ) = a 0 + a 1 x , где a 1 ≠ 0 ,представляет собой наклонную линию с точкой пересечения с осью Y a 0 и наклоном a 1 .
- График полинома 2-й степениf ( x ) = a 0 + a 1 x + a 2 x 2 , где a 2 ≠ 0представляет собой параболу .
- График полинома 3-й степениf ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 , где a 3 ≠ 0является кубической кривой .
- График любого многочлена степени 2 или вышеf ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + an x n , где an ≠ 0 и n ≥ 2представляет собой непрерывную нелинейную кривую.
Неконстантная полиномиальная функция стремится к бесконечности , когда переменная неограниченно возрастает (по абсолютной величине ). Если степень больше единицы, график не имеет асимптоты . Он имеет две параболические ветви с вертикальным направлением (одна ветвь для положительных x и одна для отрицательных x ).
Полиномиальные графики анализируются в исчислении с использованием пересечений, наклонов, вогнутости и поведения концов.
Уравнения
Полиномиальное уравнение , также называемое алгебраическим уравнением , представляет собой уравнение вида [24] Например, является полиномиальным уравнением.
При рассмотрении уравнений неопределенные (переменные) многочленов также называются неизвестными , а решения — это возможные значения неизвестных, для которых равенство верно (в общем случае может существовать более одного решения). Полиномиальное уравнение отличается от полиномиального тождества , например ( x + y )( x − y ) = x 2 − y 2 , где оба выражения представляют один и тот же многочлен в разных формах, и, как следствие, любая оценка обоих членов дает действительное равенство.
В элементарной алгебре такие методы, как квадратичная формула , преподаются для решения всех полиномиальных уравнений первой и второй степени с одной переменной. Существуют также формулы для кубических и четвертых уравнений . Для более высоких степеней теорема Абеля–Руффини утверждает, что не может существовать общей формулы в радикалах. Однако алгоритмы поиска корней могут использоваться для нахождения численных приближений корней полиномиального выражения любой степени.
Число решений полиномиального уравнения с действительными коэффициентами не может превышать степени и равно степени при подсчете комплексных решений с учетом их кратности . Этот факт называется основной теоремой алгебры .
Решение уравнений
Корень ненулевого одномерного многочлена P — это значение a от x , такое что P ( a ) = 0 . Другими словами, корень P — это решение полиномиального уравнения P ( x ) = 0 или ноль полиномиальной функции, определяемой P . В случае нулевого многочлена каждое число является нулем соответствующей функции, и понятие корня рассматривается редко.
Число a является корнем многочлена P тогда и только тогда, когда линейный многочлен x − a делит P , то есть если существует другой многочлен Q, такой что P = ( x − a ) Q . Может случиться, что степень (большая 1 ) числа x − a делит P ; в этом случае a является кратным корнем P , а в противном случае a является простым корнем P . Если P является ненулевым многочленом, существует наивысшая степень m такая , что ( x − a ) m делит P , что называется кратностью a как корня P . Число корней ненулевого многочлена P , подсчитанное с их соответствующими кратностями, не может превышать степени P , [25] и равно этой степени, если рассматриваются все комплексные корни ( это следствие основной теоремы алгебры ). Коэффициенты многочлена и его корни связаны формулами Виета .
Некоторые многочлены, такие как x 2 + 1 , не имеют корней среди действительных чисел . Однако, если множество принятых решений расширить до комплексных чисел , каждый непостоянный многочлен имеет по крайней мере один корень; это фундаментальная теорема алгебры . Последовательно разделяя множители x − a , можно увидеть, что любой многочлен с комплексными коэффициентами можно записать как константу (его старший коэффициент), умноженную на произведение таких многочленных множителей степени 1; как следствие, число (комплексных) корней, подсчитанное с их кратностями, в точности равно степени многочлена.
Может быть несколько значений «решения уравнения» . Можно захотеть выразить решения в виде явных чисел; например, единственное решение 2 x − 1 = 0 равно 1/2 . Это, как правило, невозможно для уравнений степени больше единицы, и с древних времен математики пытались выразить решения в виде алгебраических выражений ; например, золотое сечение является единственным положительным решением В древние времена им это удалось только для степеней один и два. Для квадратных уравнений квадратная формула дает такие выражения решений. С XVI века похожие формулы (использующие кубические корни в дополнение к квадратным корням), хотя и гораздо более сложные, известны для уравнений третьей и четвертой степени (см. кубическое уравнение и уравнение четвертой степени ). Но формулы для степени 5 и выше ускользали от исследователей в течение нескольких столетий. В 1824 году Нильс Хенрик Абель доказал поразительный результат, что существуют уравнения степени 5, решения которых не могут быть выражены (конечной) формулой, включающей только арифметические операции и радикалы (см. теорему Абеля–Руффини ). В 1830 году Эварист Галуа доказал, что большинство уравнений степени выше четвертой не могут быть решены радикалами, и показал, что для каждого уравнения можно решить, разрешимо ли оно радикалами, и, если да, решить его. Этот результат ознаменовал начало теории Галуа и теории групп , двух важных разделов современной алгебры . Сам Галуа отмечал, что вычисления, подразумеваемые его методом, были невыполнимы. Тем не менее, формулы для разрешимых уравнений степеней 5 и 6 были опубликованы (см. функция пятой степени и уравнение секстики ).
Когда нет алгебраического выражения для корней, и когда такое алгебраическое выражение существует, но слишком сложно, чтобы быть полезным, единственный способ решения — вычислить численные приближения решений. [26] Для этого существует много методов; некоторые из них ограничены полиномами, а другие могут применяться к любой непрерывной функции . Наиболее эффективные алгоритмы позволяют легко решать (на компьютере ) полиномиальные уравнения степени выше 1000 (см. Алгоритм поиска корня ).
Для полиномов с более чем одной неизвестной комбинации значений переменных, для которых полиномиальная функция принимает значение ноль, обычно называются нулями, а не «корнями». Изучение множеств нулей полиномов является предметом алгебраической геометрии . Для набора полиномиальных уравнений с несколькими неизвестными существуют алгоритмы для определения, имеют ли они конечное число комплексных решений, и, если это число конечно, для вычисления решений. См. Система полиномиальных уравнений .
Частный случай, когда все многочлены имеют степень один, называется системой линейных уравнений , для которой существует другой ряд различных методов решения , включая классический метод исключения Гаусса .
Полиномиальное уравнение, для которого интересны только решения, являющиеся целыми числами, называется диофантовым уравнением . Решение диофантовых уравнений, как правило, является очень сложной задачей. Доказано, что не может быть общего алгоритма для их решения или даже для определения того, является ли множество решений пустым (см. десятую проблему Гильберта ). Некоторые из самых известных задач, решенных за последние пятьдесят лет, связаны с диофантовыми уравнениями, например, Великая теорема Ферма .
Полиномиальные выражения
Часто рассматриваются многочлены, в которых неопределенные величины заменяются некоторыми другими математическими объектами, и иногда они имеют специальное название.
Тригонометрические полиномы
Тригонометрический полином — это конечная линейная комбинация функций sin ( nx ) и cos( nx ), где n принимает значения одного или нескольких натуральных чисел . [27] Коэффициенты могут быть взяты как действительные числа для действительных функций.
Если sin( nx ) и cos( nx ) разложить по sin( x ) и cos( x ), тригонометрический многочлен станет многочленом от двух переменных sin( x ) и cos( x ) (используя Список тригонометрических тождеств#Формулы для нескольких углов ). И наоборот, каждый многочлен от sin( x ) и cos( x ) может быть преобразован с помощью тождеств произведения в сумму в линейную комбинацию функций sin( nx ) и cos( nx ). Эта эквивалентность объясняет, почему линейные комбинации называются многочленами.
Для комплексных коэффициентов нет никакой разницы между такой функцией и конечным рядом Фурье .
Тригонометрические полиномы широко используются, например, в тригонометрической интерполяции, применяемой для интерполяции периодических функций . Они также используются в дискретном преобразовании Фурье .
Матричные полиномы
Матричный полином — это полином с квадратными матрицами в качестве переменных. [28] При наличии обычного скалярного полинома этот полином оценивается в матрице A , где I — единичная матрица . [29]
Матричное полиномиальное уравнение — это равенство между двумя матричными полиномами, которое выполняется для конкретных рассматриваемых матриц. Матричное полиномиальное тождество — это матричное полиномиальное уравнение, которое выполняется для всех матриц A в указанном матричном кольце M n ( R ).
Экспоненциальные полиномы
Двумерный полином, в котором вторая переменная заменяется экспоненциальной функцией, примененной к первой переменной, например P ( x , e x ) , можно назвать экспоненциальным полиномом .
Связанные концепции
Рациональные функции
Рациональная дробь — это частное ( алгебраическая дробь ) двух многочленов. Любое алгебраическое выражение , которое можно переписать в виде рациональной дроби, является рациональной функцией .
В то время как полиномиальные функции определены для всех значений переменных, рациональная функция определена только для тех значений переменных, для которых знаменатель не равен нулю.
Рациональные дроби включают в себя многочлены Лорана, но не ограничивают знаменатели степенями неопределенности.
полиномы Лорана
Полиномы Лорана похожи на полиномы, но допускают появление отрицательных степеней переменных.
Ряд мощности
Формальные степенные ряды похожи на многочлены, но допускают бесконечно много ненулевых членов, так что они не имеют конечной степени. В отличие от многочленов их в общем случае нельзя явно и полностью записать (как и иррациональные числа ), но правила манипулирования их членами такие же, как и для многочленов. Неформальные степенные ряды также обобщают многочлены, но произведение двух степенных рядов может не сходиться.
Кольцо полиномов
Многочлен f над коммутативным кольцом R — это многочлен, все коэффициенты которого принадлежат R. Легко проверить, что многочлены в заданном наборе неизвестных над R образуют коммутативное кольцо, называемое кольцом многочленов от этих неизвестных, обозначаемое в одномерном случае и в многомерном случае.
Итак , большую часть теории многомерного случая можно свести к итеративному одномерному случаю.
Отображение из R в R [ x ], переводящее r в себя, рассматриваемое как постоянный многочлен, является инъективным кольцевым гомоморфизмом , посредством которого R рассматривается как подкольцо R [ x ] . В частности, R [ x ] является алгеброй над R .
Можно представить себе кольцо R [ x ] как возникающее из R путем добавления одного нового элемента x к R и расширяющееся минимальным образом до кольца, в котором x не удовлетворяет никаким другим соотношениям, кроме обязательных, плюс коммутация со всеми элементами R (то есть xr = rx ). Для этого нужно также сложить все степени x и их линейные комбинации.
Формирование кольца многочленов, вместе с формированием колец множителей путем разложения идеалов , являются важными инструментами для построения новых колец из известных. Например, кольцо (фактически поле) комплексных чисел, которое может быть построено из кольца многочленов R [ x ] над действительными числами путем разложения идеала кратных многочлену x 2 + 1 . Другим примером является построение конечных полей , которое выполняется аналогичным образом, начиная с поля целых чисел по модулю некоторого простого числа в качестве кольца коэффициентов R (см. модульную арифметику ).
Если R коммутативно, то можно связать с каждым полиномом P в R [ x ] полиномиальную функцию f с областью определения и областью определения, равными R . (В более общем смысле, можно взять область определения и область определения любой той же унитальной ассоциативной алгебры над R .) Значение f ( r ) получается путем подстановки значения r вместо символа x в P . Одна из причин различать полиномы и полиномиальные функции заключается в том, что над некоторыми кольцами различные полиномы могут давать одну и ту же полиномиальную функцию (см. малую теорему Ферма для примера, где R — целые числа по модулю p ). Это не так, когда R — действительные или комплексные числа, поэтому эти два понятия не всегда различаются в анализе . Еще более важная причина различать полиномы и полиномиальные функции заключается в том, что многие операции над полиномами (например, евклидово деление ) требуют рассмотрения того, из чего состоит полином, как выражения, а не его оценки при некотором постоянном значении для x .
Делимость
Если R — область целостности , а f и g — многочлены в R [ x ] , то говорят, что f делит g или f — делитель g , если существует многочлен q в R [ x ], такой что f q = g . Если тогда a является корнем f, если и только если делит f . В этом случае частное можно вычислить с помощью деления многочлена в столбик . [30] [31]
Если F — поле , а f и g — многочлены в F [ x ] с g ≠ 0 , то существуют уникальные многочлены q и r в F [ x ] с и такие, что степень r меньше степени g (используя соглашение, что многочлен 0 имеет отрицательную степень). Многочлены q и r однозначно определяются f и g . Это называется евклидовым делением , делением с остатком или полиномиальным делением в столбик и показывает, что кольцо F [ x ] является евклидовой областью .
Аналогично, простые многочлены (точнее, неприводимые многочлены ) можно определить как ненулевые многочлены, которые не могут быть разложены на множители двух непостоянных многочленов . В случае коэффициентов в кольце «непостоянный» необходимо заменить на «непостоянный или неединичный » ( оба определения совпадают в случае коэффициентов в поле). Любой многочлен можно разложить на произведение обратимой константы на произведение неприводимых многочленов. Если коэффициенты принадлежат полю или уникальной области факторизации, это разложение уникально с точностью до порядка множителей и умножения любого неединичного множителя на единицу (и деления единичного множителя на ту же единицу). Когда коэффициенты принадлежат целым числам, рациональным числам или конечному полю, существуют алгоритмы для проверки неприводимости и вычисления факторизации на неприводимые многочлены (см. Факторизация многочленов ). Эти алгоритмы не применимы для ручного вычисления, но доступны в любой системе компьютерной алгебры . Критерий Эйзенштейна также может быть использован в некоторых случаях для определения неприводимости.
Приложения
Позиционная нотация
В современных позиционных системах счисления, таких как десятичная система , цифры и их позиции в представлении целого числа, например, 45, являются сокращенной записью для многочлена в системе счисления с основанием или базой, в данном случае 4 × 10 1 + 5 × 10 0 . В качестве другого примера, в системе счисления с основанием 5 строка цифр, такая как 132, обозначает (десятичное) число 1 × 5 2 + 3 × 5 1 + 2 × 5 0 = 42. Это представление уникально. Пусть b будет положительным целым числом, большим 1. Тогда каждое положительное целое число a может быть выражено единственным образом в виде
где m — неотрицательное целое число, а r — целые числа, такие что
0 < r m < b и 0 ≤ r i < b для i = 0, 1, . . . , m − 1 . [32]
Интерполяция и аппроксимация
Простая структура полиномиальных функций делает их весьма полезными при анализе общих функций с использованием полиномиальных приближений. Важным примером в исчислении является теорема Тейлора , которая приблизительно утверждает, что каждая дифференцируемая функция локально выглядит как полиномиальная функция, и теорема Стоуна–Вейерштрасса , которая утверждает, что каждая непрерывная функция, определенная на компактном интервале действительной оси, может быть приближена на всем интервале сколь угодно близко полиномиальной функцией. Практические методы приближения включают полиномиальную интерполяцию и использование сплайнов . [33]
Другие приложения
Полиномы часто используются для кодирования информации о каком-либо другом объекте. Характеристический полином матрицы или линейного оператора содержит информацию о собственных значениях оператора . Минимальный полином алгебраического элемента записывает простейшее алгебраическое отношение, которому удовлетворяет этот элемент. Хроматический полином графа подсчитывает количество правильных раскрасок этого графа.
Термин «полиномиальный» как прилагательное может также использоваться для величин или функций, которые могут быть записаны в полиномиальной форме. Например, в теории сложности вычислений фраза полиномиальное время означает, что время, необходимое для завершения алгоритма, ограничено полиномиальной функцией некоторой переменной, например, размера входных данных.
История
Определение корней многочленов, или «решение алгебраических уравнений», является одной из старейших задач в математике. Однако элегантная и практичная система обозначений, которую мы используем сегодня, появилась только в XV веке. До этого уравнения записывались словами. Например, алгебраическая задача из «Китайской арифметики в девяти разделах» , ок. 200 г. до н. э. , начинается словами: «Три снопа хорошего урожая, два снопа посредственного урожая и один сноп плохого урожая продаются за 29 доу». Мы бы записали 3 x + 2 y + z = 29 .
История обозначения
Самое раннее известное использование знака равенства содержится в «Точильном камне Витте » Роберта Рекорда (1557). Знаки + для сложения, − для вычитания и использование буквы для неизвестного появляются в «Arithemetica integra » Михаэля Штифеля (1544). Рене Декарт в «La géometrie» (1637) ввел понятие графика полиномиального уравнения. Он популяризировал использование букв из начала алфавита для обозначения констант и букв из конца алфавита для обозначения переменных, как можно видеть выше, в общей формуле для полинома от одной переменной, где a s обозначают константы, а x обозначает переменную. Декарт также ввел использование верхних индексов для обозначения показателей степеней. [34]
Смотрите также
Примечания
- ^ Борегар и Фрели (1973, стр. 153)
- ^ Бремя и ярмарки (1993, стр. 96)
- ^ Фрейли (1976, стр. 245)
- ^ Маккой (1968, стр. 190)
- ^ Моисей (1967, стр. 82)
- ↑ См. «полином» и «биномиальный», Компактный Оксфордский словарь английского языка.
- ^ ab Weisstein, Eric W. "Polynomial". mathworld.wolfram.com . Получено 28.08.2020 .
- ^ ab "Многочлены | Brilliant Math & Science Wiki". brilliant.org . Получено 28.08.2020 .
- ^ abc Barbeau 2003, стр. 1–2
- ^ Вайсштейн, Эрик В. «Нулевой многочлен». MathWorld .
- ^ Эдвардс 1995, стр. 78
- ^ abc Эдвардс, Гарольд М. (1995). Линейная алгебра. Springer. стр. 47. ISBN 978-0-8176-3731-6.
- ^ Саломон, Дэвид (2006). Кодирование для передачи данных и компьютерных коммуникаций. Springer. стр. 459. ISBN 978-0-387-23804-3.
- ^ ab Введение в алгебру. Yale University Press. 1965. стр. 621.
Любые два таких многочлена можно складывать, вычитать или умножать. Более того, результатом в каждом случае является другой многочлен
- ^ Криете, Хартье (20 мая 1998 г.). Прогресс в голоморфной динамике. ЦРК Пресс. п. 159. ИСБН 978-0-582-32388-9.
Этот класс эндоморфизмов замкнут относительно композиции,
- ^ Маречек, Линн; Матис, Андреа Ханикатт (6 мая 2020 г.). Промежуточная алгебра 2e. OpenStax . §7.1.
- ^ Хейлок, Дерек; Кокберн, Энн Д. (2008-10-14). Понимание математики для маленьких детей: руководство для учителей базовой ступени и младших классов. SAGE. стр. 49. ISBN 978-1-4462-0497-9.
Мы обнаруживаем, что множество целых чисел не замкнуто относительно этой операции деления.
- ^ аб Маречек и Матис, 2020, §5.4]
- ^ Селби, Питер Х.; Славин, Стив (1991). Практическая алгебра: Самоучитель (2-е изд.). Wiley. ISBN 978-0-471-53012-1.
- ^ Weisstein, Eric W. "Ruffini's Rule". mathworld.wolfram.com . Получено 25.07.2020 .
- ^ Барбо 2003, стр. 80–2
- ^ Барбо 2003, стр. 64–5
- ^ Варберг, Перселл и Ригдон 2007, стр. 38.
- ^ Проскуряков, И.В. (1994). «Алгебраическое уравнение». В Хазевинкеле, Михил (ред.). Энциклопедия математики . Том. 1. Спрингер. ISBN 978-1-55608-010-4.
- ^ Leung, Kam-tim; et al. (1992). Полиномы и уравнения. Hong Kong University Press. стр. 134. ISBN 9789622092716.
- ^ Макнами, Дж. М. (2007). Численные методы для корней многочленов, часть 1. Elsevier. ISBN 978-0-08-048947-6.
- ^ Powell, Michael JD (1981). Теория и методы аппроксимации . Cambridge University Press . ISBN 978-0-521-29514-7.
- ^ Гохберг, Израиль; Ланкастер, Питер; Родман, Лейба (2009) [1982]. Матричные многочлены . Классика прикладной математики. Том 58. Ланкастер, Пенсильвания: Общество промышленной и прикладной математики . ISBN 978-0-89871-681-8. Збл 1170.15300.
- ^ Хорн и Джонсон 1990, стр. 36.
- ^ Ирвинг, Рональд С. (2004). Целые числа, многочлены и кольца: курс алгебры. Springer. стр. 129. ISBN 978-0-387-20172-6.
- ^ Джексон, Терренс Х. (1995). От многочленов к суммам квадратов. CRC Press. стр. 143. ISBN 978-0-7503-0329-3.
- ^ Маккой 1968, стр. 75
- ^ де Вильерс, Иоганн (2012). Математика приближения. Спрингер. ISBN 9789491216503.
- ^ Ивс, Говард (1990). Введение в историю математики (6-е изд.). Saunders. ISBN 0-03-029558-0.
- ^ Коэффициентом члена может быть любое число из указанного множества. Если это множество является множеством действительных чисел, мы говорим о "многочленах над действительными числами". Другие распространенные виды многочленов — это многочлены с целыми коэффициентами, многочлены с комплексными коэффициентами и многочлены с коэффициентами, которые являются целыми числами по модулю некоторого простого числа p .
- ^ Эта терминология появилась в то время, когда не было четкого различия между многочленом и функцией, которую он определяет: постоянный член и постоянный многочлен определяют постоянные функции . [ необходима ссылка ]
- ^ Фактически, как однородная функция , она однородна в любой степени. [ необходима ссылка ]
- ^ Некоторые авторы используют «моном» для обозначения « монома ». См. Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra . Springer. стр. 457. ISBN 978-0-8176-4522-9.
- ^ В этом параграфе предполагается, что многочлены имеют коэффициенты в поле .
Ссылки
- Барбо, Э.Дж. (2003). Полиномы. Спрингер. ISBN 978-0-387-40627-5.
- Борегард, Рэймонд А.; Фрейли, Джон Б. (1973), Первый курс линейной алгебры: с дополнительным введением в группы, кольца и поля , Бостон: Houghton Mifflin Company , ISBN 0-395-14017-X
- Бронштейн, Мануэль и др., ред. (2006). Решение полиномиальных уравнений: основы, алгоритмы и приложения. Springer. ISBN 978-3-540-27357-8.
- Берден, Ричард Л.; Фейрес, Дж. Дуглас (1993), Численный анализ (5-е изд.), Бостон: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
- Каэн, Поль-Жан; Шабер, Жан-Люк (1997). Целочисленные полиномы. Американское математическое общество. ISBN 978-0-8218-0388-2.
- Фрейли, Джон Б. (1976), Первый курс абстрактной алгебры (2-е изд.), Чтение: Addison-Wesley , ISBN 0-201-01984-1
- Хорн, Роджер А.; Джонсон, Чарльз Р. (1990). Матричный анализ . Cambridge University Press . ISBN 978-0-521-38632-6..
- Ланг, Серж (2002), Алгебра , Graduate Texts in Mathematics , т. 211 (пересмотренное третье издание), Нью-Йорк: Springer-Verlag, ISBN 978-0-387-95385-4, г-н 1878556. Эта классическая книга охватывает большую часть содержания данной статьи.
- Leung, Kam-tim; et al. (1992). Полиномы и уравнения. Hong Kong University Press. ISBN 9789622092716.
- Майр, К. (1937). «Über die Auflösung алгебраический Gleichungssysteme durch Hypergeometrische Funktionen». Монашефте по математике и физике . 45 : 280–313. дои : 10.1007/BF01707992. S2CID 197662587.
- Маккой, Нил Х. (1968), Введение в современную алгебру, пересмотренное издание , Бостон: Allyn and Bacon , LCCN 68015225
- Моисе, Эдвин Э. (1967), Исчисление: Полное , Чтение: Эддисон-Уэсли
- Прасолов, Виктор В. (2005). Полиномы. Springer. ISBN 978-3-642-04012-2.
- Sethuraman, BA (1997). "Многочлены". Кольца, поля и векторные пространства: введение в абстрактную алгебру через геометрическую конструктивность . Springer. ISBN 978-0-387-94848-5.
- Тот, Габор (2021). «Многочленные выражения». Элементы математики . Бакалаврские тексты по математике. стр. 263–318. doi :10.1007/978-3-030-75051-0_6. ISBN 978-3-030-75050-3.
- Umemura, H. (2012) [1984]. "Разрешение алгебраических уравнений с помощью тета-констант". В Mumford, David (ред.). Tata Lectures on Theta II: Jacobian theta functions and Differential Labs . Springer. стр. 261–. ISBN 978-0-8176-4578-6.
- Варберг, Дейл Э.; Перселл, Эдвин Дж.; Ригдон, Стивен Э. (2007). Исчисление (9-е изд.). Пирсон Прентис Холл . ISBN 978-0131469686.
- фон Линдеманн, Ф. (1884). «Ueber die Auflösung der алгебраишен Gleichungen durch transcente Functionen». Нахрихтен фон дер Кёнигль. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen . 1884 : 245–8.
- фон Линдеманн, Ф. (1892). «Ueber die Auflösung der алгебраического Gleichungen durch transcente Functionen. II». Нахрихтен фон дер Кёнигль. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen . 1892 : 245–8.
Внешние ссылки
- Маркушевич, А.И. (2001) [1994], "Многочлен", Энциклопедия математики , Издательство ЭМС
- «Исследования Эйлера о корнях уравнений». Архивировано из оригинала 24 сентября 2012 г.







































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)





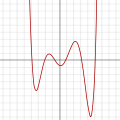







![{\displaystyle R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce54622cb380383ab3a42441b056626ea0d2440)
![{\displaystyle R[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c388e003e234e12fb55533e35a211c8cf295e5)
![{\displaystyle R[x_{1},\ldots ,x_{n}]=\left(R[x_{1},\ldots ,x_{n-1}]\right)[x_{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0bbfe1bccac6aa10e3a7daba9b95381c6f05bd)





