Математика и искусство


| Часть серии статей о | ||
| Математика | ||
|---|---|---|
 Математический портал Математический портал | ||
Математика и искусство связаны различными способами. Математика сама по себе описывается как искусство, мотивированное красотой . Математику можно различить в таких видах искусства, как музыка , танец , живопись , архитектура , скульптура и текстиль . Однако эта статья посвящена математике в изобразительном искусстве.
Математика и искусство имеют давнюю историческую связь. Художники использовали математику с 4 века до н. э., когда греческий скульптор Поликлет написал свой Канон , предписывающий пропорции, которые, как предполагалось, были основаны на соотношении 1: √ 2 для идеальной мужской наготы. Были сделаны постоянные популярные заявления об использовании золотого сечения в античном искусстве и архитектуре, без надежных доказательств. В эпоху итальянского Возрождения Лука Пачоли написал влиятельный трактат De divina ratione (1509), иллюстрированный гравюрами на дереве Леонардо да Винчи , об использовании золотого сечения в искусстве. Другой итальянский художник, Пьеро делла Франческа , развил идеи Евклида о перспективе в таких трактатах, как De Prospectiva Pingendi , и в своих картинах. Гравер Альбрехт Дюрер сделал много ссылок на математику в своей работе Melencolia I. В наше время художник-график М. К. Эшер с помощью математика Х. С. М. Коксетера интенсивно использовал тесселяцию и гиперболическую геометрию , в то время как движение «Де Стиль» во главе с Тео ван Дусбургом и Питом Мондрианом явно приняло геометрические формы. Математика вдохновила текстильные искусства, такие как стегание , вязание , вышивка крестиком , крючком , вышивка , ткачество , турецкое и другое ковроделие , а также килим . В исламском искусстве симметрия очевидна в таких разнообразных формах, как персидская гирих и марокканская плитка зеллидж , могольские проколотые каменные экраны джали и широко распространенные своды мукарнас .
Математика напрямую повлияла на искусство с помощью концептуальных инструментов, таких как линейная перспектива , анализ симметрии и математических объектов, таких как многогранники и лента Мёбиуса . Магнус Веннингер создает красочные звездчатые многогранники , изначально как модели для обучения. Математические концепции, такие как рекурсия и логический парадокс, можно увидеть в картинах Рене Магритта и в гравюрах М. К. Эшера. Компьютерное искусство часто использует фракталы , включая множество Мандельброта , и иногда исследует другие математические объекты, такие как клеточные автоматы . Спорно, художник Дэвид Хокни утверждал, что художники, начиная с эпохи Возрождения, использовали камеру -люциду для рисования точных изображений сцен; архитектор Филип Стедман аналогичным образом утверждал, что Вермеер использовал камеру-обскуру в своих отчетливо наблюдаемых картинах.
Другие связи включают алгоритмический анализ произведений искусства с помощью рентгеновской флуоресцентной спектроскопии , открытие того, что традиционные батики из разных регионов Явы имеют различные фрактальные измерения , и стимулы к математическим исследованиям, особенно теорию перспективы Филиппо Брунеллески , которая в конечном итоге привела к проективной геометрии Жирара Дезарга . Устойчивая точка зрения, основанная в конечном счете на пифагорейском представлении о гармонии в музыке, утверждает, что все было организовано Числом, что Бог является геометром мира, и что поэтому геометрия мира священна .
Истоки: от Древней Греции до эпохи Возрождения
ПоликлетаКанонисимметрия

Поликлет старший (ок. 450–420 до н. э.) был греческим скульптором из школы Аргоса и современником Фидия . Его работы и статуи в основном были из бронзы и изображали атлетов. По словам философа и математика Ксенократа , Поликлет считается одним из самых важных скульпторов классической античности за его работу над Дорифором и статуей Геры в Герайоне Аргоса . [3] Хотя его скульптуры, возможно, не так известны, как скульптуры Фидия, ими восхищаются. В своем Каноне , трактате, который он написал, чтобы задокументировать «идеальные» пропорции тела обнаженной мужской натуры, Поликлет дает нам математический подход к скульптуре человеческого тела. [3]
Сам Канон был утерян , но предполагается, что Поликлет использовал последовательность пропорций, где каждая длина равна длине диагонали квадрата, нарисованного на предыдущем, 1: √ 2 (примерно 1:1,4142). [4]
Влияние канона Поликлета огромно в классической греческой , римской и ренессансной скульптуре, и многие скульпторы следовали предписаниям Поликлета. Хотя ни одна из оригинальных работ Поликлета не сохранилась, римские копии демонстрируют его идеал физического совершенства и математической точности. Некоторые ученые утверждают, что пифагорейская мысль повлияла на канон Поликлета. [5] Канон применяет основные математические концепции греческой геометрии, такие как отношение, пропорция и симметрия (по-гречески «гармоничные пропорции») , и превращает ее в систему, способную описывать человеческую форму посредством ряда непрерывных геометрических прогрессий . [4]
Перспектива и пропорция

В классические времена, вместо того, чтобы уменьшать удаленные фигуры с помощью линейной перспективы , художники определяли размер объектов и фигур в соответствии с их тематической важностью. В Средние века некоторые художники использовали обратную перспективу для особого акцента. Мусульманский математик Альхазен (Ибн аль-Хайсам) описал теорию оптики в своей Книге оптики в 1021 году, но никогда не применял ее к искусству. [6] В эпоху Возрождения произошло возрождение классической греческой и римской культуры и идей, среди которых было изучение математики для понимания природы и искусств . Два основных мотива подтолкнули художников позднего Средневековья и эпохи Возрождения к математике. Во-первых, художникам нужно было выяснить, как изображать трехмерные сцены на двухмерном холсте. Во-вторых, философы и художники были убеждены, что математика является истинной сущностью физического мира и что вся вселенная, включая искусство, может быть объяснена в геометрических терминах. [7]
Зачатки перспективы появились с Джотто (1266/7 – 1337), который пытался рисовать в перспективе, используя алгебраический метод для определения расположения удаленных линий. В 1415 году итальянский архитектор Филиппо Брунеллески и его друг Леон Баттиста Альберти продемонстрировали геометрический метод применения перспективы во Флоренции, используя подобные треугольники , сформулированные Евклидом, для нахождения кажущейся высоты удаленных объектов. [8] [9] Собственные перспективные картины Брунеллески утеряны, но картина Мазаччо Святой Троицы показывает его принципы в действии. [6] [10] [11]
_01.jpg/440px-San_Romano_Battle_(Paolo_Uccello,_London)_01.jpg)
Итальянский художник Паоло Уччелло (1397–1475) был очарован перспективой, как показано в его картинах « Битва при Сан-Романо» (ок. 1435–1460): сломанные копья удобно расположены вдоль линий перспективы. [12] [13]
Художник Пьеро делла Франческа (ок. 1415–1492) был примером этого нового сдвига в мышлении итальянского Возрождения. Он был опытным математиком и геометром , писал книги по стереометрии и перспективе , включая De prospectiva pingendi (О перспективе в живописи) , Trattato d'Abaco (Трактат об абаке) и De quinque corporibus regularibus (О пяти правильных телах) . [14] [15] [16] Историк Вазари в своих «Жизнеописаниях художников» называет Пьеро «величайшим геометром своего времени, или, возможно, любого времени». [17] Интерес Пьеро к перспективе можно увидеть в его картинах, включая Полиптих Перуджи , [18] алтарь Сан-Агостино и «Бичевание Христа» . Его работа по геометрии оказала влияние на более поздних математиков и художников, включая Луку Пачоли в его De divina ratione и Леонардо да Винчи . Пьеро изучал классическую математику и труды Архимеда . [19] Его обучали коммерческой арифметике в «школах абака»; его труды отформатированы как школьные учебники абака, [20] возможно, включая Liber Abaci Леонардо Пизано ( Фибоначчи ) 1202 года . Линейная перспектива только вводилась в художественный мир. Альберти объяснил в своем труде 1435 года De pictura : «световые лучи движутся по прямым линиям от точек наблюдаемой сцены к глазу, образуя своего рода пирамиду с глазом в качестве вершины». Картина, построенная с использованием линейной перспективы, является поперечным сечением этой пирамиды. [21]
В De Prospectiva Pingendi Пьеро преобразует свои эмпирические наблюдения за тем, как аспекты фигуры изменяются с точкой зрения, в математические доказательства. Его трактат начинается в духе Евклида: он определяет точку как «мельчайшую вещь, которую глаз может постичь». [a] [7] Он использует дедуктивную логику , чтобы подвести читателя к перспективному представлению трехмерного тела. [22]
Художник Дэвид Хокни утверждал в своей книге « Тайное знание: повторное открытие утраченных техник старых мастеров» , что художники начали использовать камеру-люциду с 1420-х годов, что привело к внезапному изменению точности и реализма, и что эта практика была продолжена крупными художниками, включая Энгра , Ван Эйка и Караваджо . [23] Критики расходятся во мнениях относительно того, был ли Хокни прав. [24] [25] Аналогичным образом, архитектор Филипп Стедман спорно утверждал [26] , что Вермеер использовал другое устройство, камеру-обскуру , чтобы помочь ему создавать свои отличительно наблюдаемые картины. [27]
В 1509 году Лука Пачоли (ок. 1447–1517) опубликовал De divina ratione о математической и художественной пропорции , в том числе в человеческом лице. Леонардо да Винчи (1452–1519) иллюстрировал текст гравюрами на дереве правильных тел, пока учился у Пачоли в 1490-х годах. Рисунки Леонардо, вероятно, являются первыми иллюстрациями скелетных тел. [28] Они, такие как ромбокубооктаэдр , были одними из первых, которые были нарисованы для демонстрации перспективы путем наложения друг на друга. В работе обсуждается перспектива в работах Пьеро делла Франческа , Мелоццо да Форли и Марко Пальмеццано . [29] Леонардо изучал Summa Пачоли , из которой он скопировал таблицы пропорций. [30] В «Моне Лизе» и «Тайной вечере » Леонардо использовал линейную перспективу с точкой схода для создания кажущейся глубины. [31] «Тайная вечеря» построена в строгом соотношении 12:6:4:3, как и «Афинская школа » Рафаэля , на которой изображен Пифагор с табличкой идеальных пропорций, священной для пифагорейцев. [32] [33] В «Витрувианском человеке » Леонардо выразил идеи римского архитектора Витрувия , новаторски показав мужскую фигуру дважды и поместив ее в центр как круга, так и квадрата. [34]
Еще в XV веке криволинейная перспектива нашла свое применение в картинах художников, интересующихся искажениями изображений. «Портрет четы Арнольфини» Яна ван Эйка 1434 года содержит выпуклое зеркало с отражениями людей на сцене, [35] в то время как « Автопортрет в выпуклом зеркале» Пармиджанино , ок. 1523–1524 годов, показывает в основном неискаженное лицо художника в центре с сильно изогнутым фоном и рукой художника по краю. [36]
Трехмерное пространство может быть убедительно представлено в искусстве, как в техническом рисунке , средствами, отличными от перспективы. Косые проекции , включая кавалерийскую перспективу (использовавшуюся французскими военными художниками для изображения укреплений в 18 веке), постоянно и повсеместно использовались китайскими художниками с первого или второго века до 18 века. Китайцы заимствовали эту технику из Индии, которая заимствовала ее из Древнего Рима. Косая проекция наблюдается в японском искусстве, например, в картинах Укиё-э Тории Киёнаги (1752–1815). [37]
- Гравюра на дереве из работы Луки Пачоли «О божественной пропорции» (1509) с равносторонним треугольником на человеческом лице
- Камера-люцида в использовании. Scientific American , 1879
- Иллюстрация художника, использующего камеру-обскуру . XVII век.
- Теория перспективы Брунеллески : «Тринита » Мазаччо , ок. 1426–1428, в базилике Санта-Мария-Новелла.
- Криволинейная перспектива : выпуклое зеркало в картине Яна ван Эйка « Портрет четы Арнольфини» , 1434 г.
- Пармиджанино , Автопортрет в выпуклом зеркале , ок. 1523–1524 гг.
- Пифагор с таблицей пропорций на картине Рафаэля « Афинская школа» , 1509 г.
- Косая проекция : Вход и двор ямыня . Фрагмент свитка о Сучжоу , написанного Сюй Яном по заказу императора Цяньлуна . XVIII век
- Косая проекция : женщины играют в настольные игры сёги , го и бан-сугороку . Картина Тории Киёнаги , Япония, около 1780 г.
Золотое сечение
Золотое сечение (примерно равное 1,618) было известно Евклиду . [38] В наше время постоянно утверждалось, что золотое сечение [39] [40] [41] [42] использовалось в искусстве и архитектуре древними в Египте, Греции и других местах, без надежных доказательств. [43] Это утверждение может быть результатом путаницы с «золотым сечением», которое для древних греков означало «избегание излишеств в любом направлении», а не соотношение. [43] Пирамидологи с 19 - го века спорили о сомнительных математических основаниях для золотого сечения в дизайне пирамид. [b] Парфенон , храм V века до н. э. в Афинах, как утверждалось, использовал золотое сечение в своем фасаде и плане этажа, [47] [48] [49] но эти утверждения также опровергаются измерениями. [43] Также утверждалось, что Великая мечеть Кайруана в Тунисе использовала золотое сечение в своем дизайне, [ 50 ] но это соотношение не появляется в оригинальных частях мечети. [51] Историк архитектуры Фредерик Макоди Лунд утверждал в 1919 году, что Шартрский собор (XII век), Нотр-Дам де Лан (1157–1205) и Нотр-Дам де Пари (1160) спроектированы в соответствии с золотым сечением, [52] рисуя регулирующие линии, чтобы доказать свою правоту. Другие ученые утверждают, что до работы Пачоли в 1509 году золотое сечение было неизвестно художникам и архитекторам. [53] Например, высота и ширина фасада Нотр-Дам де Лан имеют соотношение 8/5 или 1,6, а не 1,618. Такие соотношения Фибоначчи быстро становится трудно отличить от золотого сечения. [54] После Пачоли золотое сечение стало более определённо различимым в произведениях искусства, включая «Мону Лизу» Леонардо . [55]
Другое отношение, единственное другое морфическое число, [56] было названо пластическим числом [c] в 1928 году голландским архитектором Хансом ван дер Лааном (первоначально названным le nombre radiant на французском языке). [57] Его значение является решением кубического уравнения
- ,
иррациональное число, которое приблизительно равно 1,325. По словам архитектора Ричарда Падована , это имеет характерные соотношения 3/4 и 1/7 , которые управляют пределами человеческого восприятия в отношении одного физического размера к другому. Ван дер Лаан использовал эти соотношения при проектировании церкви аббатства Св. Бенедиктусберга в Нидерландах в 1967 году. [57]
- Соотношения основания к гипотенузе (b:a) для пирамиды Хуфу могут быть: 1:φ ( треугольник Кеплера ), 3:5 ( треугольник 3-4-5 ) или 1:4/π
- Предполагаемые соотношения: Нотр-Дам в Лаоне.
- Золотые прямоугольники, наложенные на Мону Лизу
- Церковь аббатства Св. Бенедикта 1967 года , спроектированная Хансом ван дер Лааном, имеет пластичные пропорции.
Плоские симметрии

Плоская симметрия на протяжении тысячелетий использовалась в таких произведениях искусства, как ковры , решетки, текстиль и плитка. [59] [60] [61] [62]
Многие традиционные ковры, будь то ворсовые ковры или плоские тканые килимы , разделены на центральное поле и обрамляющую кайма; оба могут иметь симметрию, хотя в коврах ручной работы она часто слегка нарушается мелкими деталями, вариациями рисунка и изменениями в цвете, внесенными ткачом. [59] В килимах из Анатолии используемые мотивы сами по себе обычно симметричны. Общая планировка также обычно присутствует с такими расположениями, как полосы, полосы, чередующиеся с рядами мотивов, и упакованные массивы примерно шестиугольных мотивов. Поле обычно выкладывается как обои с группой обоев, такой как pmm, в то время как граница может быть выложена как фриз группы фриза pm11, pmm2 или pma2. Турецкие и среднеазиатские килимы часто имеют три или более кайма в разных группах фриза. Ткачи, безусловно, имели намерение симметрии, без явного знания ее математики. [59] Математик и теоретик архитектуры Никос Салингарос предполагает, что «мощное присутствие» [58] (эстетический эффект) «великого ковра» [58], такого как лучшие двухмедальонные ковры Коньи 17-го века, создается математическими методами, связанными с теориями архитектора Кристофера Александра . Эти методы включают создание пары противоположностей; противопоставление цветовых значений; геометрическое разделение областей, будь то с помощью дополнительных форм или балансировки направленности острых углов; обеспечение мелкомасштабной сложности (от уровня узла и выше) и как мелко-, так и крупномасштабной симметрии; повторяющиеся элементы в иерархии различных масштабов (с соотношением около 2,7 от каждого уровня к следующему). Салингарос утверждает, что «все успешные ковры удовлетворяют по крайней мере девяти из десяти приведенных выше правил», и предполагает, что можно было бы создать метрику из этих правил. [58]
Сложные решетки встречаются в индийской работе Джали , высеченной в мраморе для украшения гробниц и дворцов. [60] Китайские решетки, всегда с некоторой симметрией, присутствуют в 14 из 17 групп обоев; они часто имеют зеркальную, двойную зеркальную или вращательную симметрию. Некоторые имеют центральный медальон, а некоторые имеют границу в группе фриза. [63] Многие китайские решетки были проанализированы математически Дэниелом С. Дайем; он определяет Сычуань как центр ремесла. [64]
Симметрии заметны в текстильном искусстве , включая стеганое шитье , [61] вязание , [65] вышивку крестиком , вязание крючком , [66] вышивку [67] [68] и ткачество , [69] где они могут быть чисто декоративными или могут быть признаками статуса. [70] Вращательная симметрия обнаруживается в круглых структурах, таких как купола ; они иногда искусно украшены симметричными узорами внутри и снаружи, как в мечети шейха Лотфоллы 1619 года в Исфахане . [71] Элементы вышивки и кружевной работы, такие как скатерти и коврики для стола, изготовленные с использованием коклюшек или фриволите , могут иметь широкий спектр отражательной и вращательной симметрии, которые исследуются математически. [72]
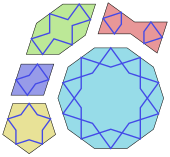
Исламское искусство использует симметрию во многих своих художественных формах, особенно в мозаиках гирих . Они образованы с использованием набора из пяти форм плиток, а именно правильного десятиугольника, вытянутого шестиугольника, галстука-бабочки, ромба и правильного пятиугольника. Все стороны этих плиток имеют одинаковую длину; и все их углы кратны 36° (π/5 радиан ), предлагая пятикратную и десятикратную симметрию. Плитки украшены полосатыми линиями (гирих), как правило, более заметными, чем границы плиток. В 2007 году физики Питер Лу и Пол Стейнхардт утверждали, что гирих напоминает квазикристаллические мозаики Пенроуза . [73] Сложная геометрическая плитка зеллидж является отличительным элементом марокканской архитектуры. [62] Своды Мукарнаса трехмерны, но были спроектированы в двух измерениях с рисунками геометрических ячеек. [74]
- Хотамис килим (фрагмент), Центральная Анатолия , начало 19 века
- Деталь парчи эпохи династии Мин , в которой использован узор в виде скошенной шестиугольной решетки.
- Симметрия : гобелен с узором «Флорентийский Барджелло»
- Потолок мечети шейха Лютфоллы , Исфахан , 1619 г.
- Плитки гирих : узоры в крупном и мелком масштабе на своде из святилища Дарб-и Имам , Исфахан, 1453 г.
- Сложная геометрия и мозаичные покрытия сводов мукарнаса в мечети шейха Лотфоллы в Исфахане
- Архитектурный план свода квартала Мукарнас. Свиток Топкапы
Многогранники
Платоновы тела и другие многогранники являются повторяющейся темой в западном искусстве. Они встречаются, например, в мраморной мозаике с изображением малого звёздчатого додекаэдра , приписываемого Паоло Уччелло, на полу базилики Сан-Марко в Венеции; [12] в диаграммах Леонардо да Винчи правильных многогранников, нарисованных в качестве иллюстраций к книге Луки Пачоли 1509 года «Божественная пропорция» ; [12] в виде стеклянного ромбокубооктаэдра на портрете Пачоли работы Якопо де Барбари, написанном в 1495 году; [12] в усечённом многограннике (и различных других математических объектах) на гравюре Альбрехта Дюрера «Меланхолия I» ; [12] и на картине Сальвадора Дали «Тайная вечеря» , на которой Христос и его ученики изображены внутри гигантского додекаэдра . [75]
Альбрехт Дюрер (1471–1528) был немецким гравером эпохи Возрождения, который внес важный вклад в литературу о многогранниках в своей книге 1525 года Underweysung der Messung (Образование измерений) , предназначенной для обучения предметам линейной перспективы , геометрии в архитектуре , Платоновых тел и правильных многоугольников . Дюрер, вероятно, находился под влиянием работ Луки Пачоли и Пьеро делла Франческа во время своих поездок в Италию . [76] Хотя примеры перспективы в Underweysung der Messung недостаточно развиты и содержат неточности, в ней подробно обсуждается многогранники. Дюрер также первым ввел в текст идею многогранных сеток , многогранников, развернутых так, чтобы они лежали плоско для печати. [77] В 1528 году Дюрер опубликовал еще одну влиятельную книгу о человеческих пропорциях под названием «Vier Bücher von Menschlicher Proportion» («Четыре книги о человеческих пропорциях»). [78]
Известная гравюра Дюрера «Меланхолия I» изображает разочарованного мыслителя, сидящего рядом с усеченным треугольным трапецоэдром и магическим квадратом . [1] Эти два объекта и гравюра в целом стали предметом более современной интерпретации, чем содержание практически любой другой гравюры, [1] [79] [80] включая двухтомную книгу Петера-Клауса Шустера, [81] и влиятельное обсуждение в монографии Эрвина Панофски о Дюрере. [1] [82]
Картина Сальвадора Дали 1954 года «Тело Гиперкуба» уникальным образом изображает крест Христа как развернутую трехмерную сетку для гиперкуба , также известного как тессеракт : развертывание тессеракта в эти восемь кубов аналогично развертыванию сторон куба в крестообразную форму из шести квадратов, здесь представляя божественную перспективу с четырехмерным правильным многогранником. [83] [84] На картине изображена фигура Христа перед тессарактом; обычно его изображают прибитым гвоздями к кресту, но на картине гвоздей нет. Вместо этого перед его телом, по углам переднего из восьми кубов тессаракта, находятся четыре маленьких куба. Математик Томас Банчофф утверждает, что Дали пытался выйти за рамки трехмерного мира, в то время как поэт и художественный критик Келли Гровьер говорит, что «картина, кажется, разорвала связь между духовностью спасения Христа и материальностью геометрических и физических сил. Кажется, она преодолевает пропасть, которая, по мнению многих, разделяет науку и религию». [85]
- Первая печатная иллюстрация ромбокубооктаэдра Леонардо да Винчи , опубликованная в De Divina Proportione , 1509 г.
Фрактальные измерения

Традиционные индонезийские рисунки батика с воском на ткани сочетают в себе изобразительные мотивы (такие как цветочные и растительные элементы) с абстрактными и несколько хаотичными элементами, включая неточность в нанесении воскового резиста и случайные вариации, вносимые растрескиванием воска. Узоры батика имеют фрактальную размерность от 1 до 2, варьирующуюся в разных региональных стилях. Например, батик Чиребона имеет фрактальную размерность 1,1; батики Джокьякарты и Суракарты (Соло) в Центральной Яве имеют фрактальную размерность от 1,2 до 1,5; а батики Ласема на северном побережье Явы и Тасикмалая на Западной Яве имеют фрактальную размерность от 1,5 до 1,7. [86]
Работы современного художника Джексона Поллока , работающего в технике капельной живописи, также отличаются своей фрактальной размерностью. Его картина 14 1948 года имеет размерность, подобную береговой линии, 1,45, в то время как его более поздние картины имели последовательно более высокие фрактальные размерности и, соответственно, более сложные узоры. Одна из его последних работ, Blue Poles , была создана за шесть месяцев и имеет фрактальную размерность 1,72. [87]
Сложные отношения
Астроном Галилео Галилей в своем труде Il Saggiatore писал, что «[Вселенная] написана на языке математики , а ее персонажи — треугольники, круги и другие геометрические фигуры». [88] Художники, которые стремятся и стремятся изучать природу, должны, по мнению Галилея, сначала полностью понять математику. Математики, наоборот, стремились интерпретировать и анализировать искусство через призму геометрии и рациональности. Математик Фелипе Кукер предполагает, что математика, и особенно геометрия, является источником правил для «художественного творчества, основанного на правилах», хотя и не единственным. [89] Некоторые из многочисленных нитей получившихся сложных отношений [90] описаны ниже.

Математика как искусство
Математик Джерри П. Кинг описывает математику как искусство, заявляя, что «ключи к математике — красота и элегантность, а не унылость и техничность», и что красота — движущая сила математических исследований. [91] Кинг цитирует эссе математика Г. Х. Харди 1940 года «Апология математика» . В нем Харди обсуждает, почему он считает две теоремы классических времен первоклассными, а именно доказательство Евклида о том, что существует бесконечно много простых чисел , и доказательство того, что квадратный корень из 2 иррационален . Кинг оценивает последнее по критериям Харди для математической элегантности : « серьёзность, глубина, общность, неожиданность, неизбежность и экономия » (курсив Кинга), и описывает доказательство как «эстетически приятное». [92] Венгерский математик Пауль Эрдёш соглашался, что математика обладает красотой, но считал, что причины этого не поддаются объяснению: «Почему числа красивы? Это все равно, что спрашивать, почему прекрасна Девятая симфония Бетховена . Если вы не понимаете, почему, никто не сможет вам сказать. Я знаю, что числа красивы». [93]
Математические инструменты для искусства
Математику можно различить во многих видах искусства, таких как музыка , танец , [94] живопись , архитектура и скульптура . Каждое из них тесно связано с математикой. [95] Среди связей с изобразительным искусством математика может предоставить инструменты для художников, такие как правила линейной перспективы , описанные Бруком Тейлором и Иоганном Ламбертом , или методы начертательной геометрии , которые теперь применяются в программном моделировании твердых тел, начиная с Альбрехта Дюрера и Гаспара Монжа . [96] Художники, такие как Лука Пачоли в Средние века и Леонардо да Винчи и Альбрехт Дюрер в эпоху Возрождения, использовали и развивали математические идеи в своих художественных работах. [95] [97] Использование перспективы началось, несмотря на некоторые зачаточные применения в архитектуре Древней Греции, с итальянских художников, таких как Джотто в 13 веке; Такие правила, как точка схода, были впервые сформулированы Брунеллески примерно в 1413 году, [6] его теория оказала влияние на Леонардо и Дюрера. Работа Исаака Ньютона по оптическому спектру повлияла на теорию цветов Гете и, в свою очередь , на таких художников, как Филипп Отто Рунге , Дж. М. У. Тернер , [98] прерафаэлиты и Василий Кандинский . [99] [100] Художники также могут выбрать анализ симметрии сцены. [101] Инструменты могут применяться математиками, которые исследуют искусство, или художниками, вдохновленными математикой, такими как М. К. Эшер (вдохновленный Х. С. М. Кокстером ) и архитектором Фрэнком Гери , который более убедительно утверждал, что компьютерное проектирование позволило ему выразить себя совершенно новым способом. [102]

Художник Ричард Райт утверждает, что математические объекты, которые могут быть построены, можно рассматривать либо «как процессы для моделирования явлений», либо как произведения « компьютерного искусства ». Он рассматривает природу математической мысли, отмечая, что фракталы были известны математикам за столетие до того, как они были признаны таковыми. Райт заключает, что уместно подвергать математические объекты любым методам, используемым для «согласования с культурными артефактами, такими как искусство, напряжением между объективностью и субъективностью, их метафорическими значениями и характером репрезентативных систем». Он приводит в качестве примеров изображение из множества Мандельброта , изображение, созданное клеточным автоматом , и изображение, визуализированное компьютером , и обсуждает, ссылаясь на тест Тьюринга , могут ли алгоритмические продукты быть искусством. [103] В работе Сашо Калайджиевски « Математика и искусство: введение в визуальную математику» используется аналогичный подход, рассматривающий подходящие визуальные математические темы, такие как мозаика, фракталы и гиперболическая геометрия. [104]
Некоторые из первых произведений компьютерного искусства были созданы «Drawing Machine 1» Десмонда Пола Генри , аналоговой машиной, основанной на компьютере бомбового прицела и выставленной в 1962 году. [105] [106] Машина была способна создавать сложные, абстрактные, асимметричные, криволинейные, но повторяющиеся линейные рисунки. [105] [107] Совсем недавно Хамид Надери Йеганех создал формы, напоминающие объекты реального мира, такие как рыбы и птицы, используя формулы, которые последовательно изменяются для рисования семейств кривых или наклонных линий. [108] [109] [110] Такие художники, как Микаэль Хвидтфельдт Кристенсен, создают произведения генеративного или алгоритмического искусства , написав скрипты для программной системы, такой как Structure Synth : художник эффективно направляет систему на применение желаемой комбинации математических операций к выбранному набору данных. [111] [112]
- Математическая скульптура Батшебы Гроссман , 2007 г.
- Фрактальная скульптура: 3D Fraktal 03/H/dd Хартмута Скербиша, 2003 г.
- Слово Фибоначчи : фрагмент работы Самюэля Монье, 2009 г.
- Компьютерное художественное изображение, созданное Десмондом Полом Генри , «Рисовальная машина 1», экспонировалось в 1962 году.
- «Птица в полете» , Хамид Надери Йеганех , 2016 г., построенная с помощью семейства математических кривых.
От математики к искусству

Математик и физик-теоретик Анри Пуанкаре « Наука и гипотеза» широко читали кубисты , включая Пабло Пикассо и Жана Метценже . [114] [115] Будучи хорошо знакомым с работой Бернхарда Римана по неевклидовой геометрии, Пуанкаре был более чем осведомлен о том, что евклидова геометрия является лишь одной из многих возможных геометрических конфигураций, а не абсолютной объективной истиной. Возможное существование четвертого измерения вдохновило художников подвергнуть сомнению классическую перспективу эпохи Возрождения : неевклидова геометрия стала допустимой альтернативой. [116] [117] [118] Концепция того, что живопись может быть выражена математически, в цвете и форме, способствовала кубизму, художественному движению, которое привело к абстрактному искусству . [119] Метцингер в 1910 году писал, что: «[Пикассо] излагает свободную, подвижную перспективу, из которой гениальный математик Морис Принсе вывел целую геометрию». [120] Позже Метцингер писал в своих мемуарах:
Морис Принсет часто присоединялся к нам... именно как художник он концептуализировал математику, как эстетик он призывал n -мерные континуумы. Он любил заинтересовывать художников новыми взглядами на пространство , которые были открыты Шлегелем и некоторыми другими. Он преуспел в этом. [121]
Импульс к созданию учебных или исследовательских моделей математических форм естественным образом создает объекты, которые имеют симметрию и удивительные или приятные формы. Некоторые из них вдохновили художников, таких как дадаисты Ман Рэй [122] , Марсель Дюшан [123] и Макс Эрнст [ 124] [125] и после Ман Рэя Хироши Сугимото [126] .

Ман Рэй сфотографировал некоторые математические модели в Институте Анри Пуанкаре в Париже, включая Objet mathematique (Математический объект). Он отметил, что это представляло поверхности Эннепера с постоянной отрицательной кривизной , полученные из псевдосферы . Эта математическая основа была важна для него, так как позволяла ему отрицать, что объект был «абстрактным», вместо этого утверждая, что он был таким же реальным, как писсуар, который Дюшан превратил в произведение искусства. Ман Рэй признал, что формула объекта [поверхности Эннепера] «ничего не значила для меня, но сами формы были такими же разнообразными и подлинными, как и любые в природе». Он использовал свои фотографии математических моделей в качестве фигур в своей серии, которую он сделал по пьесам Шекспира , например, в своей картине 1934 года «Антоний и Клеопатра» . [127] Арт-репортер Джонатан Китс, пишущий в ForbesLife , утверждает, что Ман Рэй фотографировал «эллиптические параболоиды и конические точки в том же чувственном свете, что и его фотографии Кики де Монпарнас », и «гениально переосмысливает холодные математические вычисления, чтобы раскрыть топологию желания». [128] Скульпторы двадцатого века, такие как Генри Мур , Барбара Хепуорт и Наум Габо, черпали вдохновение в математических моделях. [129] Мур писал о своей работе 1938 года «Струнная мать и дитя »: «Несомненно, источником моих струнных фигур был Музей науки ... Я был очарован математическими моделями, которые я там увидел... Меня волновало не научное изучение этих моделей, а возможность смотреть сквозь струны, как через птичью клетку, и видеть одну форму внутри другой». [130]

Художники Тео ван Дусбург и Пит Мондриан основали движение De Stijl , в котором они хотели «создать визуальный словарь, состоящий из элементарных геометрических форм, понятных всем и адаптируемых к любой дисциплине». [131] [132] Многие из их произведений искусства визуально состоят из разлинованных квадратов и треугольников, иногда также с кругами. Художники De Stijl работали в области живописи, мебели, дизайна интерьеров и архитектуры. [131] После распада De Stijl ван Дусбург основал авангардное движение Art Concret , описав свою «Арифметическую композицию » 1929–1930 годов , серию из четырех черных квадратов по диагонали квадратного фона, как «структуру, которой можно управлять, определенную поверхность без случайных элементов или индивидуального каприза», но «не лишенную духа, не лишенную универсальности и не ... пустую, поскольку есть все , что соответствует внутреннему ритму». Искусствовед Глэдис Фабр отмечает, что в картине задействованы две прогрессии, а именно: растущие черные квадраты и чередующиеся фоны. [133]
Математика тесселяции , многогранники, формирование пространства и самореференция обеспечили художника-графика М. К. Эшера (1898—1972) материалами для его гравюр на дереве на всю жизнь. [134] [135] В « Наброске Альгамбры» Эшер показал, что искусство может быть создано с помощью многоугольников или правильных форм, таких как треугольники, квадраты и шестиугольники. Эшер использовал неправильные многоугольники при замощении плоскости и часто использовал отражения, скользящие отражения и переводы для получения дополнительных узоров. Многие из его работ содержат невозможные конструкции, созданные с использованием геометрических объектов, которые создают противоречие между перспективной проекцией и тремя измерениями, но приятны для человеческого зрения. « Восхождение и спуск » Эшера основаны на « невозможной лестнице », созданной ученым-медиком Лайонелом Пенроузом и его сыном математиком Роджером Пенроузом . [136] [137] [138]
Некоторые из многочисленных тесселяционных рисунков Эшера были вдохновлены беседами с математиком Х. С. М. Коксетером о гиперболической геометрии . [139] Эшер был особенно заинтересован в пяти конкретных многогранниках, которые много раз появляются в его работах. Платоновы тела — тетраэдры, кубы, октаэдры, додекаэдры и икосаэдры — особенно заметны в «Порядке и хаосе» и «Четырех правильных телах» . [140] Эти звездчатые фигуры часто находятся внутри другой фигуры, что еще больше искажает угол обзора и конформацию многогранников и обеспечивает многогранную перспективную работу. [141]
Визуальная сложность математических структур, таких как мозаики и многогранники, вдохновила множество математических произведений искусства. Стюарт Коффин создает многогранные головоломки из редких и красивых пород дерева; Джордж У. Харт работает над теорией многогранников и создает скульптуры, вдохновленные ими; Магнус Веннингер создает «особенно красивые» модели сложных звездчатых многогранников . [142]
Искаженные перспективы анаморфоза исследовались в искусстве с шестнадцатого века, когда Ганс Гольбейн Младший включил сильно искаженный череп в свою картину 1533 года «Послы» . Многие художники с тех пор, включая Эшера, использовали анаморфные приемы. [143]
Математика топологии вдохновила нескольких художников современности. Скульптор Джон Робинсон (1935–2007) создал такие работы, как «Гордиев узел» и «Обручи дружбы» , демонстрирующие теорию узлов в полированной бронзе. [7] Другие работы Робинсона исследуют топологию торов . Книга Бытия основана на кольцах Борромео — наборе из трех окружностей, никакие две из которых не связаны, но в которых вся структура не может быть разобрана без разрушения. [144] Скульптор Хеламан Фергюсон создает сложные поверхности и другие топологические объекты . [145] Его работы являются визуальными представлениями математических объектов; «Восьмеричный путь» основан на проективной специальной линейной группе PSL(2,7) , конечной группе из 168 элементов. [146] [147] Скульптор Батшеба Гроссман аналогичным образом основывает свою работу на математических структурах. [148] [149] Художник Нельсон Сайерс включает в свое искусство математические концепции и теоремы от топосов и схем до теоремы о четырех цветах и иррациональности числа π . [150]
Проект по исследованию гуманитарных наук изучает связи между математикой и искусством посредством ленты Мёбиуса , флексагонов , оригами и панорамной фотографии. [151]
Математические объекты, включая многообразие Лоренца и гиперболическую плоскость, были созданы с использованием волоконного искусства , включая вязание крючком. [d] [153] Американская ткачиха Ада Диц написала в 1949 году монографию «Алгебраические выражения в текстильных изделиях ручной работы» , в которой определила узоры ткачества, основанные на разложении многомерных полиномов . [154] Математик Дайна Тайминя продемонстрировала особенности гиперболической плоскости с помощью вязания крючком в 2001 году. [155] Это побудило Маргарет и Кристину Вертхайм связать крючком коралловый риф , состоящий из множества морских животных, таких как голожаберники , формы которых основаны на гиперболических плоскостях. [156] Математик Дж. К. П. Миллер использовал клеточный автомат Правила 90 для проектирования гобеленов, изображающих как деревья, так и абстрактные узоры из треугольников. [157] «Математики» [158] Пэт Эшфорт и Стив Пламмер используют вязаные версии математических объектов, таких как гексафлексагоны, в своем обучении, хотя их губка Менгера оказалась слишком сложной для вязания и вместо этого была сделана из пластиковой парусины. [159] [160] Их проект «матганы» (афганцы для школ) ввел вязание в британскую программу по математике и технологиям. [161] [162]
- Четырехмерное пространство в кубизме : «Эспри Жуффре » 1903 года «Элементарный трактат о геометрии в четырех измерениях» . [163] [е]
- Де Стиль : Геометрическая композиция I (Натюрморт) Тео ван Дусбурга , 1916 год.
- От педагогики к искусству: Магнус Веннингер с некоторыми из своих звездчатых многогранников , 2009 г.
- Шарф -лента Мёбиуса , связанный крючком , 2007 г.
- Анаморфизм : «Послы» Ганса Гольбейна Младшего , 1533 г., с сильно искаженным черепом на переднем плане.
- Вязаный коралловый риф : множество животных, смоделированных в виде гиперболических плоскостей с различными параметрами Маргарет и Кристин Вертхайм . Föhr Reef , Тюбинген, 2013

Иллюстрирование математики


Моделирование — далеко не единственный возможный способ иллюстрации математических концепций. Триптих Стефанески Джотто , 1320 г., иллюстрирует рекурсию в форме mise en abyme ; центральная панель триптиха содержит, слева внизу, коленопреклоненную фигуру кардинала Стефанески, держащего триптих в качестве подношения. [165] Метафизические картины Джорджо де Кирико , такие как его «Большой метафизический интерьер» 1917 г. , исследуют вопрос уровней репрезентации в искусстве, изображая картины внутри своих картин. [166]
Искусство может служить примером логических парадоксов, как в некоторых картинах сюрреалиста Рене Магритта , которые можно читать как семиотические шутки о путанице между уровнями. В «Человеческом состоянии» (1933) Магритт изображает мольберт (на реальном холсте), плавно поддерживающий вид через окно, которое обрамлено «реальными» шторами на картине. Аналогично, « Галерея гравюр» Эшера (1956) — это гравюра, изображающая искаженный город, содержащий галерею, которая рекурсивно содержит картину, и так до бесконечности . [167] Магритт использовал сферы и кубоиды, чтобы исказить реальность другим способом, рисуя их рядом с набором домов в своей «Ментальной арифметике» 1931 года , как будто это были детские строительные блоки, но размером с дом. [168] The Guardian заметила, что «жуткий образ игрушечного города» предсказал узурпацию модернизмом «уютных традиционных форм», но также играет с человеческой склонностью искать закономерности в природе . [169]

Последняя картина Сальвадора Дали «Хвост ласточки» (1983) была частью серии, вдохновленной теорией катастроф Рене Тома . [ 171] Испанский художник и скульптор Пабло Паласуэло (1916–2007) сосредоточился на исследовании формы. Он разработал стиль, который он описал как геометрию жизни и геометрию всей природы. Состоящий из простых геометрических форм с подробным рисунком и окраской, в таких работах, как «Угловой I» и «Оно» , Паласуэло выразил себя в геометрических преобразованиях. [7]
Художник Адриан Грей практикует балансировку камней , используя трение и центр тяжести для создания поразительных и, казалось бы, невозможных композиций. [172]

Художники, однако, не обязательно воспринимают геометрию буквально. Как пишет Дуглас Хофштадтер в своих размышлениях 1980 года о человеческом мышлении, Гёделе, Эшере, Бахе , посредством (помимо прочего) математики искусства: «Разница между рисунком Эшера и неевклидовой геометрией заключается в том, что в последнем случае для неопределенных терминов можно найти понятные интерпретации, что приводит к понятным общим системам, тогда как в первом случае конечный результат несовместим с чьим-либо представлением о мире, независимо от того, как долго мы смотрим на картины». Хофштадтер обсуждает, казалось бы, парадоксальную литографию Print Gallery М. К. Эшера; на ней изображен приморский город, содержащий художественную галерею, которая, кажется, содержит картину приморского города, причем существует «странная петля или запутанная иерархия» уровней реальности на изображении. Сам художник, замечает Хофштадтер, не виден; его реальность и его отношение к литографии не парадоксальны. [170] Центральная пустота изображения также привлекла внимание математиков Барта де Смита и Хендрика Ленстры , которые предполагают, что она может содержать копию эффекта Дросте себя, повернутую и сжатую; это было бы еще одной иллюстрацией рекурсии, выходящей за рамки отмеченной Хофштадтером. [173] [174]
Анализ истории искусств
Алгоритмический анализ изображений произведений искусства, например, с использованием рентгеновской флуоресцентной спектроскопии , может раскрыть информацию об искусстве. Такие методы могут раскрыть изображения в слоях краски, позже перекрытых художником; помочь историкам искусства визуализировать произведение искусства до того, как оно потрескалось или выцвело; помочь отличить копию от оригинала или отличить стиль мазка кисти мастера от стиля его учеников. [175] [176]

Стиль капельной живописи Джексона Поллока [ 177] имеет определенное фрактальное измерение ; [178] среди художников, которые могли повлиять на контролируемый хаос Поллока , [179] Макс Эрнст рисовал фигуры Лиссажу непосредственно, размахивая проколотым ведром с краской по холсту. [180]
Ученый-компьютерщик Нил Доджсон исследовал, можно ли охарактеризовать картины Бриджит Райли с полосами математически, и пришел к выводу, что хотя расстояние разделения может «дать некоторую характеристику», а глобальная энтропия работает на некоторых картинах, автокорреляция не срабатывает, поскольку узоры Райли нерегулярны. Локальная энтропия работает лучше всего и хорошо коррелирует с описанием, данным критиком искусства Робертом Кудиелкой. [181]
В работе американского математика Джорджа Биркгоффа «Эстетическая мера » 1933 года предлагается количественная метрика эстетического качества произведения искусства. Она не пытается измерить коннотации произведения, например, что может означать картина, а ограничивается «элементами порядка» многоугольной фигуры. Сначала Биркгофф объединяет (в виде суммы) пять таких элементов: есть ли вертикальная ось симметрии; есть ли оптическое равновесие; сколько вращательных симметрий у нее есть; насколько фигура похожа на обои; и есть ли неудовлетворительные особенности, такие как наличие двух вершин слишком близко друг к другу. Эта метрика, O , принимает значение от −3 до 7. Вторая метрика, C , подсчитывает элементы фигуры, которые для многоугольника представляют собой количество различных прямых линий, содержащих хотя бы одну из его сторон. Затем Биркгофф определяет свою эстетическую меру красоты объекта как O/C . Это можно интерпретировать как баланс между удовольствием, которое доставляет созерцание объекта, и количеством усилий, необходимых для его восприятия. Предложение Биркгофа подвергалось критике по-разному, не в последнюю очередь за попытку вложить красоту в формулу, но он никогда не утверждал, что делал это. [182]
Стимулы к математическим исследованиям
Искусство иногда стимулировало развитие математики, как, например, когда теория перспективы Брунеллески в архитектуре и живописи положила начало циклу исследований, которые привели к работам Брука Тейлора и Иоганна Генриха Ламберта по математическим основам перспективного рисунка [183] и, в конечном итоге, к математике проективной геометрии Жирара Дезарга и Жана-Виктора Понселе . [184]
Японское искусство складывания бумаги оригами было математически переработано Томоко Фусе с использованием модулей , конгруэнтных листов бумаги, таких как квадраты, и превращением их в многогранники или мозаики. [185] Складывание бумаги использовалось в 1893 году Т. Сундара Рао в его «Геометрических упражнениях по складыванию бумаги» для демонстрации геометрических доказательств. [186] Математика складывания бумаги была исследована в теореме Маекавы , [187] теореме Кавасаки , [188] и аксиомах Хузиты–Хатори . [189]
- Стимул к проективной геометрии : диаграмма Альберти , показывающая круг, рассматриваемый в перспективе как эллипс . Делла Питтура , 1435–1436
От иллюзии к оп-арту

Оптические иллюзии, такие как спираль Фрейзера, поразительно демонстрируют ограничения человеческого зрительного восприятия, создавая то, что историк искусств Эрнст Гомбрих назвал «сбивающим с толку трюком». Черно-белые веревки, которые, как кажется, образуют спирали, на самом деле являются концентрическими кругами . Стиль оптического искусства или оптического искусства середины двадцатого века в живописи и графике использовал такие эффекты для создания впечатления движения и мерцающих или вибрирующих узоров, которые можно увидеть в работах таких художников, как Бриджит Райли , Спирос Хоремис, [191] и Виктор Вазарели . [192]
Сакральная геометрия
Направление искусства, начиная с Древней Греции, рассматривает Бога как геометра мира, и поэтому геометрия мира является священной. Вера в то, что Бог создал вселенную в соответствии с геометрическим планом, имеет древние истоки. Плутарх приписывал эту веру Платону , написав, что «Платон сказал, что Бог геометризирует непрерывно» ( Convivialium disputationum , liber 8,2). Этот образ с тех пор оказал влияние на западную мысль. Платоновская концепция, в свою очередь, произошла от пифагорейского понятия гармонии в музыке, где ноты были расположены в идеальных пропорциях, соответствующих длине струн лиры; действительно, пифагорейцы считали, что все было упорядочено Числом. Точно так же в платоновской мысли правильные или платоновы тела диктуют пропорции, встречающиеся в природе и в искусстве. [193] [194] Иллюстрации в Codex Vindobonensis XIII века показывают Бога, рисующего вселенную с помощью циркуля, что может быть отсылкой к стиху из Ветхого Завета: «Когда Он устраивал небеса, я был там; когда Он проводил круговую черту по лицу бездны» (Притчи 8:27). [195] В 1596 году математик-астроном Иоганн Кеплер смоделировал вселенную как набор вложенных Платоновых тел, определяя относительные размеры орбит планет. [195] « Ветхий днями » Уильяма Блейка ( изображающий Уризена , воплощение разума и закона Блейка) и его картина физика Исаака Ньютона , обнаженного, сгорбившегося и рисующего циркулем, используют символику циркуля для критики традиционного разума и материализма как ограниченных. [196] [197] Картина Сальвадора Дали 1954 года «Распятие» (Corpus Hypercubus) изображает крест как гиперкуб , представляя божественную перспективу с четырьмя измерениями вместо обычных трех. [84] В картине Дали «Таинство Тайной Вечери» (1955) Христос и его ученики изображены внутри гигантского додекаэдра . [198]
- Бог-геометр. Кодекс Виндобоненсис , c. 1220
- Создание, с изображением Пантократора . Библия Людовика Святого , ок. 1220–1240 гг.
- Модель платоновых тел Иоганна Кеплера , описывающая расположение планет в Солнечной системе, из «Mysterium Cosmographicum» , 1596 г.
- Уильям Блейк « Ветхий днями» , 1794 г.
- «Ньютон » Уильяма Блейка , ок. 1800 г.
Смотрите также
Примечания
- ^ На итальянском языке Пьеро: «una cosa tanto picholina quanto e возможно ad ochio comprendere».
- ^ Отношение наклонной высоты к половине длины основания составляет 1,619, менее 1% от золотого сечения, что предполагает использование треугольника Кеплера (угол грани 51°49'). [43] [44] Однако другие соотношения находятся в пределах погрешности измерения той же формы, и исторические свидетельства свидетельствуют о том, что, скорее всего, использовались простые целочисленные соотношения. [45] [46]
- ^ « Пластик » — способность принимать выбранную трехмерную форму.
- ↑ Изображения и видео вязаного крючком коллектора Лоренца Хинке Осинга попали в международные телевизионные новости, как можно увидеть на связанном веб-сайте. [152]
- ↑ Морис Принсе подарил копию Пабло Пикассо , чьи альбомы для рисования «Авиньонских девиц» иллюстрируют влияние Жуффре. [114] [164]
Ссылки
- ^ abcd Циглер, Гюнтер М. (3 декабря 2014 г.). «Многогранник Дюрера: 5 теорий, объясняющих безумный куб Меленколии». The Guardian . Получено 27 октября 2015 г.
- ^ ab Colombo, C.; Del Bimbo, A.; Pernici, F. (2005). «Метрическая 3D-реконструкция и получение текстуры поверхностей вращения из одного некалиброванного вида». Труды IEEE по анализу образов и машинному интеллекту . 27 (1): 99–114. CiteSeerX 10.1.1.58.8477 . doi :10.1109/TPAMI.2005.14. PMID 15628272. S2CID 13387519.
- ^ ab Stewart, Andrew (ноябрь 1978 г.). «Поликлет из Аргоса», Сто греческих скульпторов: их карьера и сохранившиеся работы». Журнал эллинских исследований . 98 : 122–131. doi : 10.2307/630196. JSTOR 630196. S2CID 162410725.
- ^ ab Тобин, Ричард (октябрь 1975 г.). « Канон Поликлета». Американский журнал археологии . 79 (4): 307–321. doi :10.2307/503064. JSTOR 503064. S2CID 191362470.
- ^ Равен, Дж. Э. (1951). «Поликлет и пифагореизм». Classical Quarterly . 1 (3–4): 147–. doi :10.1017/s0009838800004122. S2CID 170092094.
- ^ abc O'Connor, JJ; Robertson, EF (январь 2003 г.). «Математика и искусство – перспектива». Университет Сент-Эндрюс . Получено 1 сентября 2015 г.
- ^ abcd Эммер, Мишель, ред. (2005). Визуальный разум II . MIT Press. ISBN 978-0-262-05048-7.
- ^ Вазари, Джорджо (1550). Жизнеописания художников . Торрентино. стр. Глава о Брунеллески.
- ^ Альберти, Леон Баттиста ; Спенсер, Джон Р. (1956) [1435]. О живописи. Издательство Йельского университета.
- ^ Field, JV (1997). Изобретение бесконечности: математика и искусство в эпоху Возрождения . Oxford University Press. ISBN 978-0-19-852394-9.
- ^ Witcombe, Christopher LCE "Ресурсы истории искусств" . Получено 5 сентября 2015 г.
- ^ abcde Hart, Джордж В. «Многогранники в искусстве» . Проверено 24 июня 2015 г.
- ^ Каннингем, Лоуренс; Райх, Джон; Фихнер-Ратхус, Лоис (1 января 2014 г.). Культура и ценности: обзор западных гуманитарных наук. Cengage Learning. стр. 375. ISBN 978-1-285-44932-6.
которые иллюстрируют увлечение Уччелло перспективой. Сражающиеся бойцы сражаются на поле битвы, усеянном сломанными копьями, которые упали в почти сетчатом узоре и направлены в исчезающую точку где-то вдалеке.
- ^ делла Франческа, Пьеро (1942) [ок. 1474]. Дж. Никко Фасола (ред.). De перспектива пингэнди . Флоренция.
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ делла Франческа, Пьеро (1970) [Пятнадцатый век]. Дж. Арриги (ред.). Тратато д'Абако . Пиза.
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ делла Франческа, Пьеро (1916). Дж. Манчини (ред.). Опера «Регулярное тело» Пьетро Франчески — это дело Франчески узурпированной да Фра Лука Пачоли .
- ^ Вазари, Джорджо (1878). Дж. Миланези (ред.). Опера, том 2 . п. 490.
- ^ Зуффи, Стефано (1991). Пьеро делла Франческа . L'Unità – Mondadori Arte. п. 53.
- ^ Хит, Т. Л. (1908). Тринадцать книг «Начал» Евклида. Cambridge University Press. стр. 97.
- ^ Грендлер, П. (1995). «Чему Пьеро научился в школе: народное образование пятнадцатого века». В MA Lavin (ред.). Пьеро делла Франческа и его наследие . University Press of New England. стр. 161–176.
- ^ Альберти, Леон Баттиста ; Грейсон, Сесил (перевод) (1991). Кемп, Мартин (ред.). О живописи . Penguin Classics.
- ^ Петерсон, Марк. "Геометрия Пьеро делла Франческа". Архивировано из оригинала 2016-07-01 . Получено 2009-04-19 .
В Книге I, после некоторых элементарных построений для введения идеи о том, что видимый размер объекта на самом деле является его углом, противолежащим глазу, и ссылаясь на Элементы Евклида, книги I и VI, и Оптику Евклида, он обращается в Предложении 13 к изображению квадрата, лежащего плашмя на земле перед зрителем. Что на самом деле должен рисовать художник? После этого объекты строятся в квадрате (например, плитки, чтобы изобразить плиточный пол), и соответствующие объекты строятся в перспективе; в Книге II призмы возводятся над этими плоскими объектами, чтобы изобразить дома, колонны и т. д.; но основой метода является исходный квадрат, из которого следует все остальное.
- ^ Хокни, Дэвид (2006). Тайное знание: Возрождение утраченных приемов старых мастеров . Темза и Гудзон. ISBN 978-0-500-28638-8.
- ^ Ван Рипер, Фрэнк. «Хокни „Lucid“ Bomb в художественном истеблишменте». The Washington Post . Получено 4 сентября 2015 г.
- ↑ Марр, Эндрю (7 октября 2001 г.). «То, чего не видел глаз». The Guardian . Получено 4 сентября 2015 г.
- ^ Дженсон, Джонатан (25 апреля 2003 г.). «Интервью с Филипом Стедманом». Essential Vermeer . Получено 5 сентября 2015 г. .
- ^ Стедман, Филип (2002). Камера Вермеера: Раскрытие правды за шедеврами . Оксфорд. ISBN 978-0-19-280302-3.
- ^ Харт, Джордж . "Многогранники Луки Пачоли" . Получено 13 августа 2009 г.
- ^ Моррис, Родерик Конвей (27 января 2006 г.). «Возрождение Пальмеццано: из теней появляется художник». New York Times . Получено 22 июля 2015 г.
- ^ Calter, Paul. "Geometry and Art Unit 1". Dartmouth College . Архивировано из оригинала 21 августа 2009 года . Получено 13 августа 2009 года .
- ^ Бризио, Анна Мария (1980). Леонардо Художник . МакГроу-Хилл. ISBN 9780070079311.
- ^ Ладвейн, Майкл (2006). Леонардо да Винчи, Тайная вечеря: космическая драма и акт искупления. Temple Lodge Publishing. С. 61–62. ISBN 978-1-902636-75-7.
- ^ Тернер, Ричард А. (1992). Изобретение Леонардо . Альфред А. Кнопф. ISBN 9780679415510.
- ^ Вулховер, Натали (31 января 2012 г.). «Копировал ли Леонардо да Винчи своего знаменитого «Витрувианского человека»?». NBC News . Получено 27 октября 2015 г.
- ^ Криминизи, А.; Кемпц, М.; Канг, С.Б. (2004). «Отражения реальности у Яна ван Эйка и Роберта Кампена» (PDF) . Исторические методы . 37 (3): 109–121. doi :10.3200/hmts.37.3.109-122. S2CID 14289312.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 299–300, 306–307. ISBN 978-0-521-72876-8.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 269–278. ISBN 978-0-521-72876-8.
- ^ Джойс, Дэвид Э. (1996). «Элементы Евклида, Книга II, Предложение 11». Университет Кларка . Получено 24 сентября 2015 г.
- ^ Seghers, MJ; Longacre, JJ; Destefano, GA (1964). «Золотая пропорция и красота». Пластическая и реконструктивная хирургия . 34 (4): 382–386. doi :10.1097/00006534-196410000-00007. S2CID 70643014.
- ^ Майнцер, Клаус (1996). Симметрии природы: Справочник по философии природы и науки . Вальтер де Грюйтер. стр. 118.
- ^ "Математические свойства в древних театрах и амфитеатрах". Архивировано из оригинала 15 июля 2017 года . Получено 29 января 2014 года .
- ^ "Архитектура: Эллипс?". The-Colosseum.net. Архивировано из оригинала 11 декабря 2013 года . Получено 29 января 2014 года .
- ^ abcd Марковски, Джордж (январь 1992 г.). «Заблуждения о золотом сечении» (PDF) . The College Mathematics Journal . 23 (1): 2–19. doi :10.2307/2686193. JSTOR 2686193. Архивировано из оригинала (PDF) 2008-04-08 . Получено 2015-06-26 .
- ^ Тасеос, Сократ Г. (1990). Назад во времени 3104 г. до н. э. к Великой пирамиде . Издательство SOC.
- ^ Бартлетт, Кристофер (май 2014 г.). «Проект Великой пирамиды Хуфу». Nexus Network Journal . 16 (2): 299–311. doi : 10.1007/s00004-014-0193-9 . S2CID 122021107.
- ^ Герц-Фишлер, Роджер (2000). Форма Великой пирамиды . Ватерлоо, Онтарио: Wilfrid Laurier University Press . ISBN 0-88920-324-5. МР 1788996.
- ^ Хантли, Х. Э. (1970). Божественная пропорция . Дувр.
- ^ Хеменуэй, Прия (2005). Божественная пропорция: Phi в искусстве, природе и науке . Стерлинг. стр. 96.
- ^ Усват, Лилиана. «Математика Парфенона». Журнал «Математика» . Получено 24 июня 2015 г.
- ^ Boussora, Kenza; Mazouz, Said (весна 2004 г.). «Использование золотого сечения в Большой мечети Кайруана». Nexus Network Journal . 6 (1): 7–16. doi : 10.1007/s00004-004-0002-y .
Геометрическая техника построения золотого сечения, по-видимому, определила основные решения пространственной организации. Золотое сечение неоднократно появляется в некоторых частях измерений здания. Оно обнаруживается в общей пропорции плана и в размерах молитвенного пространства, двора и минарета. Наличие золотого сечения в некоторых частях мечети Кайруана указывает на то, что элементы, спроектированные и созданные с использованием этого принципа, могли быть реализованы в тот же период.
- ^ Бринкворт, Питер; Скотт, Пол (2001). «Место математики». Австралийский учитель математики . 57 (3): 2.
- ^ Чанфон Олмос, Карлос (1991). Curso sobre Proporción. Регулирование процесса строительства . Convenio de intercambio Unam-Uady. Мексика – Америка.
- ^ Ливио, Марио (2002). Золотое сечение: История Фи, самого удивительного числа в мире . Bibcode :2002grsp.book.....L. ISBN 9780767908160.
- ^ Смит, Норман А. Ф. (2001). «Cathedral Studies: Engineering or History» (PDF) . Transactions of the Newcomen Society . 73 : 95–137. doi : 10.1179/tns.2001.005. S2CID 110300481. Архивировано из оригинала 11 декабря 2015 г.
{{cite journal}}: CS1 maint: неподходящий URL ( ссылка ) - ^ Маквей, Карен (28 декабря 2009 г.). «Почему золотое сечение радует глаз: американский ученый утверждает, что знает секрет искусства». The Guardian . Получено 27 октября 2015 г.
- ^ Аартс, Дж.; Фоккинк, Р.; Крейцер, Г. (2001). «Морфические числа» (PDF) . Нью-Арк. Вискд . 5. 2 (1): 56–58.
- ^ ab Padovan, Richard (2002). Уильямс, Ким; Франциско Родригес, Хосе (ред.). «Дом Ханс ван дер Лаан и пластиковое число». Nexus IV: Архитектура и математика : 181–193.
- ^ abcd Salingaros, Nikos (ноябрь 1996 г.). «Жизнь ковра: применение правил Александра». 8-я Международная конференция по восточным коврам . Архивировано из оригинала 2016-03-05 . Получено 2015-10-02 .Перепечатано в Eiland, M.; Pinner, M., ред. (1998). Oriental Carpet and Textile Studies V. Дэнвилл, Калифорния: Конференция по восточным коврам.
- ^ abc Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 89–102. ISBN 978-0-521-72876-8.
- ^ Лернер, Мартин (1984). Пламя и лотос: искусство Индии и Юго-Восточной Азии из коллекций Кроноса (каталог выставки, ред.). Музей Метрополитен.
- ^ ab Эллисон, Элейн; Вентерс, Диана (1999). Математические одеяла: шитье не требуется . Ключевая учебная программа.
- ^ аб Кастера, Жан Марк; Перио, Франсуаза (1999). Арабески. Декоративное искусство Марокко . Реализация художественного творчества. ISBN 978-2-86770-124-5.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 103–106. ISBN 978-0-521-72876-8.
- ^ Дай, Дэниел С. (1974). Китайские решетчатые конструкции . Довер. стр. 30–39. ISBN 9780486230962.
- ^ belcastro, sarah-marie (2013). «Приключения в математическом вязании». American Scientist . 101 (2): 124. doi :10.1511/2013.101.124. Архивировано из оригинала 2016-03-04 . Получено 2015-06-24 .
- ^ Таймина, Дайна (2009). Вязание крючком приключений с гиперболическими плоскостями . AK Peters. ISBN 978-1-56881-452-0.
- ^ Снук, Барбара. Флорентийская вышивка . Scribner, Второе издание 1967.
- ^ Уильямс, Эльза С. Барджелло: Флорентийская работа на холсте . Ван Ностранд Рейнхольд, 1967.
- ^ Грюнбаум, Бранко ; Шепард, Джеффри К. (май 1980 г.). «Атлас и саржа: введение в геометрию тканей». Mathematics Magazine . 53 (3): 139–161. doi :10.2307/2690105. hdl : 10338.dmlcz/104026 . JSTOR 2690105.
- ^ ab Gamwell, Lynn (2015). Математика и искусство: Культурная история . Princeton University Press. стр. 423. ISBN 978-0-691-16528-8.
- ^ Бейкер, Патрисия Л.; Смит, Хилари (2009). Иран (3-е изд.). Bradt Travel Guides. стр. 107. ISBN 978-1-84162-289-7.
- ^ Ирвин, Вероника; Раски, Фрэнк (2014). «Разработка математической модели для кружевоплетения на коклюшках». Журнал математики и искусств . 8 (3–4): 95–110. arXiv : 1406.1532 . Bibcode :2014arXiv1406.1532I. doi :10.1080/17513472.2014.982938. S2CID 119168759.
- ^ Лу, Питер Дж.; Стейнхардт, Пол Дж. (2007). «Декагональная и квазикристаллическая мозаика в средневековой исламской архитектуре». Science . 315 (5815): 1106–1110. Bibcode :2007Sci...315.1106L. doi :10.1126/science.1135491. PMID 17322056. S2CID 10374218.
- ^ ван ден Хувен, Саския; ван дер Вин, Мартье. «Мукарнас-Математика в исламском искусстве» (PDF) . Архивировано из оригинала (PDF) 27 сентября 2013 года . Проверено 15 января 2016 г.
- ^ Марковски, Джордж (март 2005 г.). «Обзор книги: Золотое сечение» (PDF) . Notices of the American Mathematical Society . 52 (3): 344–347.
- ^ Панофски, Э. (1955). Жизнь и творчество Альбрехта Дюрера . Принстон.
- ^ Харт, Джордж У. "Многогранники Дюрера" . Получено 13 августа 2009 г.
- ^ Дюрер, Альбрехт (1528). Hierinn sind begriffen vier Bucher von menschlicher Пропорция. Нюрнберг . Проверено 24 июня 2015 г.
- ^ Шрайбер, П. (1999). «Новая гипотеза о загадочном многограннике Дюрера в его медной гравюре «Melencolia I»». Historia Mathematica . 26 (4): 369–377. doi : 10.1006/hmat.1999.2245 .
- ^ Доджсон, Кэмпбелл (1926). Альбрехт Дюрер . Лондон: Medici Society. стр. 94.
- ^ Шустер, Питер-Клаус (1991). Меланхолия I: Дюрерс Денкбильд . Берлин: Гебр. Манн Верлаг. стр. 17–83.
- ^ Панофски, Эрвин ; Клибански, Рэймонд ; Саксл, Фриц (1964). Сатурн и меланхолия. Основные книги.
- ^ Ракер, Руди (2014). Четвертое измерение: к геометрии высшей реальности. Courier Corporation. ISBN 978-0-486-79819-6.
- ^ ab "Crucifixion (Corpus Hypercubus)". Музей Метрополитен . Получено 5 сентября 2015 г.
- ^ Макдональд, Фиона (11 мая 2016 г.). «Художник, вошедший в четвертое измерение». BBC . Получено 8 февраля 2022 г.
- ^ Лукман, Мухамад; Хариади, Юн; Дестиарман, Ахмад Халдани (2007). «Батик Фрактал: от традиционного искусства к современной сложности». Proceeding Generative Art X, Милан, Италия .
- ^ Уэллетт, Дженнифер (ноябрь 2001 г.). «Фракталы Поллока». Журнал Discover . Получено 26 сентября 2016 г.
- ↑ Галилей, Галилей (1623). Пробирщик ., как переведено в Дрейк, Стиллман (1957). Открытия и мнения Галилея. Doubleday. стр. 237–238. ISBN 978-0-385-09239-5.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 381. ISBN 978-0-521-72876-8.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 10. ISBN 978-0-521-72876-8.
- ^ Кинг, Джерри П. (1992). Искусство математики . Fawcett Columbine. стр. 8–9. ISBN 978-0-449-90835-8.
- ^ Кинг, Джерри П. (1992). Искусство математики . Fawcett Columbine. стр. 135–139. ISBN 978-0-449-90835-8.
- ^ Девлин, Кит (2000). «У математиков разные мозги?». Математический ген: как развивалось математическое мышление и почему числа похожи на сплетни . Basic Books. стр. 140. ISBN 978-0-465-01619-8.
- ^ Василевска, Катажина (2012). "Математика в мире танца" (PDF) . Мосты . Получено 1 сентября 2015 г.
- ^ ab Malkevitch, Joseph. "Математика и искусство". Американское математическое общество . Получено 1 сентября 2015 г.
- ^ Малкевич, Джозеф. «Математика и искусство. 2. Математические инструменты для художников». Американское математическое общество . Получено 1 сентября 2015 г.
- ^ "Math and Art: The Good, the Bad, and the Pretty". Математическая ассоциация Америки. Архивировано из оригинала 9 сентября 2015 года . Получено 2 сентября 2015 года .
- ^ Коэн, Луиза (1 июля 2014 г.). «Как вращать цветовой круг, Тернер, Малевич и другие». Галерея Тейт . Получено 4 сентября 2015 г.
- ^ Кемп, Мартин (1992). Наука искусства: оптические темы в западном искусстве от Брунеллески до Сёра . Издательство Йельского университета. ISBN 978-968-867-185-6.
- ^ Гейдж, Джон (1999). Цвет и культура: практика и значение от античности до абстракции. Издательство Калифорнийского университета. стр. 207. ISBN 978-0-520-22225-0.
- ^ Malkevitch, Joseph. "Mathematics and Art. 3. Symmetry". American Mathematical Society . Получено 1 сентября 2015 г.
- ^ Малкевич, Джозеф. «Математика и искусство. 4. Математические художники и художники-математики». Американское математическое общество . Получено 1 сентября 2015 г.
- ^ Райт, Ричард (1988). «Некоторые вопросы развития компьютерного искусства как математической формы искусства». Leonardo . 1 (Электронное искусство, дополнительный выпуск): 103–110. doi :10.2307/1557919. JSTOR 1557919.
- ^ Калайдзиевски, Сашо (2008). Математика и искусство: Введение в визуальную математику . Чепмен и Холл. ISBN 978-1-58488-913-7.
- ^ ab Beddard, Honor (2011-05-26). "Компьютерное искусство в V&A". Музей Виктории и Альберта . Получено 22 сентября 2015 г.
- ^ «Компьютер рисует: тысячи линий в каждой». The Guardian. 17 сентября 1962 г.в Беддарде, 2015.
- ^ O'Hanrahan, Elaine (2005). Машины для рисования: Машина создавала рисунки доктора Д. П. Генри в отношении концептуальных и технологических разработок в машинном искусстве (Великобритания, 1960–1968). Неопубликованная докторская диссертация . Университет Джона Мурса, Ливерпуль.в Беддарде, 2015.
- ^ Беллос, Алекс (24 февраля 2015 г.). «Улов дня: математик ловит странную, сложную рыбу». The Guardian . Получено 25 сентября 2015 г.
- ^ ""Птица в полете (2016)", Хамид Надери Йеганех". Американское математическое общество . 23 марта 2016 г. Архивировано из оригинала 2 апреля 2019 г. Получено 6 апреля 2017 г.
- ↑ Чанг, Стефи (18 сентября 2015 г.). «Следующий да Винчи? Математический гений, использующий формулы для создания фантастических произведений искусства». CNN .
- ^ Левин, Голан (2013). «Генеративные художники». CMUEMS . Получено 27 октября 2015 г.Сюда входит ссылка на Hvidtfeldts Syntopia.
- ^ Веростко, Роман . "Алгористы" . Получено 27 октября 2015 г.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 315–317. ISBN 978-0-521-72876-8.
- ^ ab Miller, Arthur I. (2001). Einstein, Picasso: Space, Time, and the Beauty That Causes Havoc . Нью-Йорк: Basic Books. стр. 171. ISBN 978-0-465-01860-4.
- ^ Миллер, Артур И. (2012). Прозрения гения: образность и творчество в науке и искусстве . Springer. ISBN 978-1-4612-2388-7.
- ^ Хендерсон, Линда Далримпл (1983). Четвертое измерение и неевклидова геометрия в современном искусстве . Princeton University Press.
- ^ Антлифф, Марк; Лейтен, Патрисия Ди (2001). Кубизм и культура (PDF) . Темза и Гудзон. Архивировано из оригинала (PDF) 26 июля 2020 года.
- ^ Эверделл, Уильям Р. (1997). Первые модернисты: профили в истоках мысли двадцатого века. Издательство Чикагского университета. стр. 312. ISBN 978-0-226-22480-0.
- ^ Грин, Кристофер (1987). Кубизм и его враги, современные движения и реакция во французском искусстве, 1916–1928 . Издательство Йельского университета. С. 13–47.
- ^ Метцингер, Жан (октябрь – ноябрь 1910 г.). «Примечание к живописи». Пан : 60.в Miller (2001). Эйнштейн, Пикассо . Basic Books. стр. 167. ISBN 9780465018598.
- ^ Метцингер, Жан (1972). Le cubisme etait né . Присутствие изданий. стр. 43–44.в Ferry, Luc (1993). Homo Aestheticus: изобретение вкуса в демократическую эпоху. Роберт Де Лоаиза, перевод. Издательство Чикагского университета. стр. 215. ISBN 978-0-226-24459-4.
- ^ "Man Ray–Human Equations. Путешествие от математики к Шекспиру. 7 февраля – 10 мая 2015 г.". Коллекция Филлипса. 7 февраля 2015 г. Получено 5 сентября 2015 г.
- ^ Эдкок, Крейг (1987). «Эротизм Дюшана: математический анализ». Iowa Research Online . 16 (1): 149–167. Архивировано из оригинала 7 сентября 2015 г.
- ^ Элдер, Р. Брюс (2013). ДАДА, сюрреализм и кинематографический эффект. Wilfrid Laurier University Press. стр. 602. ISBN 978-1-55458-641-7.
- ^ Таббс, Роберт (2014). Математика в литературе и искусстве двадцатого века: содержание, форма, значение. JHU Press. стр. 118. ISBN 978-1-4214-1402-7.
- ^ "Концептуальные формы и математические модели Хироши Сугимото 7 февраля – 10 мая 2015 г.". Коллекция Филлипса. 7 февраля 2015 г. Получено 5 сентября 2015 г.
- ^ Таббс, Роберт (2014). Математика в литературе и искусстве 20-го века . Университет Джонса Хопкинса. С. 8–10. ISBN 978-1-4214-1380-8.
- ↑ Китс, Джонатан (13 февраля 2015 г.). «Посмотрите, как Ман Рэй сделал эллиптические параболоиды эротичными на этой выставке фотографий из коллекции Филлипса». Forbes . Получено 10 сентября 2015 г.
- ^ Гэмвелл, Линн (2015). Математика и искусство: Культурная история . Princeton University Press. С. 311–312. ISBN 978-0-691-16528-8.
- ^ Хеджко, Джон, ред. (1968). «Генри Мур: Текст на его скульптуре». Генри Спенсер Мур . Саймон и Шустер. стр. 105.
- ^ аб "Де Стиль". Глоссарий Тейта . Тейт . Проверено 11 сентября 2015 г.
- ^ Керл, Джеймс Стивенс (2006). Словарь архитектуры и ландшафтной архитектуры (второе издание). Oxford University Press. ISBN 978-0-19-860678-9.
- ^ Таббс, Роберт (2014). Математика в литературе и искусстве двадцатого века: содержание, форма, смысл . JHU Press. стр. 44–47. ISBN 978-1-4214-1402-7.
- ^ "Tour: MC Escher – Life and Work". NGA. Архивировано из оригинала 3 августа 2009 года . Получено 13 августа 2009 года .
- ^ "MC Escher". Mathacademy.com. 1 ноября 2007 г. Получено 13 августа 2009 г.
- ^ Пенроуз, Л. С.; Пенроуз, Р. (1958). «Невозможные объекты: особый тип зрительной иллюзии». British Journal of Psychology . 49 (1): 31–33. doi :10.1111/j.2044-8295.1958.tb00634.x. PMID 13536303.
- ^ Кирусис, Лефтерис М.; Пападимитриу, Христос Х. (1985). «Сложность распознавания многогранных сцен». 26-й ежегодный симпозиум по основам компьютерной науки (SFCS 1985) . стр. 175–185. CiteSeerX 10.1.1.100.4844 . doi :10.1109/sfcs.1985.59. ISBN 978-0-8186-0644-1.
- ^ Купер, Мартин (2008). «Сговорчивость интерпретации чертежей». Неравенство, поляризация и бедность . Springer-Verlag. стр. 217–230. doi :10.1007/978-1-84800-229-6_9. ISBN 978-1-84800-229-6.
- ^ Робертс, Сиобхан (2006).«Кокстеринг» с М. К. Эшером. Король бесконечного пространства: Дональд Коксетер, человек, спасший геометрию . Уокер. стр. Глава 11.
- ^ Эшер, М. К. (1988). Мир М. К. Эшера . Random House.
- ^ Эшер, М. К.; Вермейлен, М. В.; Форд, К. (1989). Эшер об Эшере: исследование бесконечности . HN Abrams.
- ^ Malkevitch, Joseph. "Mathematics and Art. 5. Polyhedras, tilings, and dissections". American Mathematical Society . Получено 1 сентября 2015 г.
- ^ Марколли, Матильда (июль 2016 г.). Понятие пространства в математике через призму современного искусства (PDF) . Century Books. стр. 23–26.
- ^ "Джон Робинсон". Bradshaw Foundation. 2007. Получено 13 августа 2009 .
- ^ "Веб-сайт Helaman Ferguson". Helasculpt.com. Архивировано из оригинала 11 апреля 2009 года . Получено 13 августа 2009 года .
- ^ Терстон, Уильям П. (1999). «Восьмеричный путь: математическая скульптура Хеламана Фергюсона». В Леви, Сильвио (ред.). Том 35: Восьмеричный путь: красота кривой четвертого порядка Клейна (PDF) . Публикации MSRI. стр. 1–7.
- ^ "Обзор книги MAA "Восьмеричный путь: красота кривой четвертой степени Кляйна". Maa.org. 14 ноября 1993 г. Архивировано из оригинала 21 декабря 2009 г. Получено 13 августа 2009 г.
- ^ "Руководство по подаркам на праздники для любителей математики". Scientific American . 23 ноября 2014 г. Получено 7 июня 2015 г.
- ^ Ханна, Рэйвен. "Галерея: Батшеба Гроссман". Журнал Symmetry . Получено 7 июня 2015 г.
- ^ Мастроянни, Брайан (26 мая 2015 г.). «Идеальное уравнение: художник сочетает математику и искусство». Fox News . Получено 28 января 2021 г.
- ^ Флерон, Джулиан Ф.; Экке, Фолькер; фон Ренессе, Кристина; Хочкисс, Филип К. (январь 2015 г.). Искусство и скульптура: математические исследования в свободных искусствах (2-е изд.). Проект «Открывая искусство математики».
- ^ Osinga, Hinke (2005). «Вязание крючком многообразия Лоренца». Оклендский университет. Архивировано из оригинала 10 апреля 2015 года . Получено 12 октября 2015 года .
- ^ Osinga, Hinke M. ; Krauskopf, Bernd (2004). «Вязание крючком многообразия Лоренца». The Mathematical Intelligencer . 26 (4): 25–37. CiteSeerX 10.1.1.108.4594 . doi :10.1007/BF02985416. S2CID 119728638. Архивировано из оригинала 2013-04-19 . Получено 2015-06-26 .
- ^ Dietz, Ada K. (1949). Algebraic Expressions in Handwoven Textiles (PDF) . Louisville, Kentucky: The Little Loomhouse. Архивировано из оригинала (PDF) 2016-02-22 . Получено 2015-06-26 .
- ^ Хендерсон, Дэвид; Таймина, Дайна (2001). «Вязание крючком гиперболической плоскости» (PDF) . Mathematical Intelligencer . 23 (2): 17–28. doi :10.1007/BF03026623. S2CID 120271314..
- ^ Барнетт, Ребекка (31 января 2017 г.). «Галерея: Что получится, если смешать математику, кораллы и вязание крючком? Это сногсшибательно». Ideas.TED.com . Получено 28 октября 2019 г. .
- ^ Миллер, JCP (1970). «Периодические леса низкорослых деревьев». Philosophical Transactions of the Royal Society of London . Series A, Mathematical and Physical Sciences. 266 (1172): 63–111. Bibcode : 1970RSPTA.266...63M. doi : 10.1098/rsta.1970.0003. JSTOR 73779. S2CID 123330469.
- ^ "Пэт Эшфорт и Стив Пламмер – Mathekniticians". Woolly Thoughts . Получено 4 октября 2015 г. .
- ^ Уорд, Марк (20 августа 2012 г.). «Вязание заново изобретено: математика, феминизм и металл». BBC News . BBC . Получено 23 сентября 2015 г. .
- ^ Эшфорт, Пэт; Пламмер, Стив. «Губка Менгера». Шерстяные мысли: в погоне за хитрой математикой . Получено 23 сентября 2015 г.
- ^ Эшфорт, Пэт; Пламмер, Стив. «Афганцы для школ». Woolly Thoughts: Mathghans . Получено 23 сентября 2015 г.
- ^ "Mathghans with a Difference". Simply Knitting Magazine . 1 июля 2008 г. Архивировано из оригинала 25 сентября 2015 г. Получено 23 сентября 2015 г.
- ^ Жуффре, Эспри (1903). Traité élémentaire de géométrie à quatre Dimensions и введение в геометрию n измерений (на французском языке). Париж: Готье-Виллар. OCLC 1445172 . Проверено 26 сентября 2015 г.
- ^ Секель, Элен (1994). «Антология ранних комментариев к Авиньонским девицам ». У Уильяма Рубина; Элен Секель; Джудит Казинс (ред.). Авиньонские девицы . Нью-Йорк: Музей современного искусства. п. 264. ИСБН 978-0-87070-162-7.
- ^ "Джотто ди Бондоне и помощники: триптих Стефанески". Ватикан . Получено 16 сентября 2015 г.
- ^ Гэмвелл, Линн (2015). Математика и искусство: Культурная история . Princeton University Press. С. 337–338. ISBN 978-0-691-16528-8.
- ↑ Купер, Джонатан (5 сентября 2007 г.). «Искусство и математика» . Получено 5 сентября 2015 г.
- ^ Хофштадтер, Дуглас Р. (1980). Гёдель, Эшер, Бах: Вечная золотая коса . Penguin. стр. 627. ISBN 978-0-14-028920-6.
- ↑ Холл, Джеймс (10 июня 2011 г.). «Рене Магритт: Принцип удовольствия – выставка». The Guardian . Получено 5 сентября 2015 г. .
- ^ ab Хофштадтер, Дуглас Р. (1980). Гёдель, Эшер, Бах: Вечная золотая коса . Penguin. стр. 98–99, 690–717. ISBN 978-0-394-74502-2.
- ^ Кинг, Эллиотт (2004). Адес, Дон (ред.). Дали . Милан: Бомпиани Арте. стр. 418–421.
- ^ "Stone balanceing" (PDF) . Monthly Maths (29). Июль 2013. Архивировано из оригинала (PDF) 16 апреля 2021 . Получено 10 июня 2017 .
- ^ де Смит, Б. (2003). «Математическая структура галереи гравюр Эшера». Notices of the American Mathematical Society . 50 (4): 446–451.
- ^ Lenstra, Hendrik; De Smit, Bart. «Applying mathematics to Escher's Print Gallery». Лейденский университет. Архивировано из оригинала 14 января 2018 года . Получено 10 ноября 2015 года .
- ^ Станек, Бекка (16 июня 2014 г.). «Ван Гог и алгоритм: как математика может спасти искусство». Журнал Time . Получено 4 сентября 2015 г.
- ^ Sipics, Michelle (18 мая 2009 г.). «Проект Ван Гога: искусство встречается с математикой в продолжающемся международном исследовании». Общество промышленной и прикладной математики. Архивировано из оригинала 7 сентября 2015 г. Получено 4 сентября 2015 г.
- ^ Эммерлинг, Леонард (2003). Джексон Поллок, 1912–1956. Ташен. п. 63. ИСБН 978-3-8228-2132-9.
- ^ Тейлор, Ричард П.; Миколич, Адам П.; Джонас, Дэвид (июнь 1999 г.). "Фрактальный анализ капельных картин Поллока". Nature . 399 (6735): 422. Bibcode :1999Natur.399..422T. doi : 10.1038/20833 . S2CID 204993516.
- ^ Тейлор, Ричард; Миколич, Адам П.; Джонас, Дэвид (октябрь 1999 г.). «Фрактальный экспрессионизм: может ли наука быть использована для дальнейшего понимания искусства?». Physics World . 12 (10): 25–28. doi :10.1088/2058-7058/12/10/21. Архивировано из оригинала 05.08.2012.
Поллок умер в 1956 году, до того, как были открыты хаос и фракталы. Поэтому крайне маловероятно, что Поллок сознательно понимал фракталы, которые он рисовал. Тем не менее, введение им фракталов было преднамеренным. Например, цвет опорного слоя был выбран для создания наиболее резкого контраста с фоном холста, и этот слой также занимает больше места на холсте, чем другие слои, что говорит о том, что Поллок хотел, чтобы этот высокофрактальный опорный слой визуально доминировал в картине. Кроме того, после завершения картин он подрезал холст, чтобы удалить области около края холста, где плотность рисунка была менее равномерной.
- ^ Кинг, М. (2002). «От Макса Эрнста до Эрнста Маха: эпистемология в искусстве и науке» (PDF) . Получено 17 сентября 2015 г.
- ^ Dodgson, NA (2012). "Математическая характеристика полосатых картин Бриджет Райли" (PDF) . Journal of Mathematics and the Arts . 5 (2–3): 89–106. doi : 10.1080/17513472.2012.679468 . S2CID 10349985.
в течение [начала] 1980-х годов узоры Райли менялись от более регулярных к более случайным (что характеризует глобальная энтропия), не теряя при этом своей ритмической структуры (что характеризует локальная энтропия). Это отражает описание Куделькой ее художественного развития.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 116–120. ISBN 978-0-521-72876-8.
- ^ Treibergs, Andrejs (24 июля 2001 г.). «Геометрия перспективного рисунка на компьютере». University of Utah . Получено 5 сентября 2015 г.
- ^ Гэмвелл, Линн (2015). Математика и искусство: Культурная история . Princeton University Press. стр. xviii. ISBN 978-0-691-16528-8.
- ^ Малкевич, Джозеф. "Математика и искусство. 6. Оригами". Американское математическое общество . Получено 1 сентября 2015 г.
- ^ Рао, Т. Сундара (1893). Геометрические упражнения по складыванию бумаги . Эддисон.
- ^ Джастин, Дж. (июнь 1986 г.). «Математика оригами, часть 9». British Origami : 28–30..
- ^ Альсина, Клауди; Нельсен, Роджер (2010). Очаровательные доказательства: путешествие в элегантную математику. Dolciani Mathematical Expositions. Том 42. Математическая ассоциация Америки . стр. 57. ISBN 978-0-88385-348-1.
- ^ Альперин, Роджер К .; Ланг, Роберт Дж. (2009). «Аксиомы одно-, двух- и многоскладчатого оригами» (PDF) . 4OSME . Архивировано из оригинала (PDF) 13.02.2022 . Получено 27.10.2015 .
- ↑ Мир геометрических игрушек, Origami Spring , август 2007 г.
- ^ Cucker, Felipe (2013). Многообразные зеркала: пересечение путей искусств и математики . Cambridge University Press. стр. 163–166. ISBN 978-0-521-72876-8.
- ^ Гэмвелл, Линн (2015). Математика и искусство: Культурная история . Princeton University Press. С. 406–410. ISBN 978-0-691-16528-8.
- ^ Ghyka, Matila (2003). Геометрия искусства и жизни . Дувр. стр. ix–xi. ISBN 978-0-486-23542-4.
- ^ Лоулор, Роберт (1982). Сакральная геометрия: философия и практика. Thames & Hudson. ISBN 978-0-500-81030-9.
- ^ ab Calter, Paul (1998). «Небесные темы в искусстве и архитектуре». Дартмутский колледж. Архивировано из оригинала 23 июня 2015 г. Получено 5 сентября 2015 г.
- ^ Мэддокс, Фиона (21 ноября 2014 г.). «10 лучших работ Уильяма Блейка». The Guardian . Получено 25 декабря 2019 г. .
- ^ "William Blake, Newton, 1795–c.1805". Tate . Октябрь 2018. Архивировано из оригинала 28 марта 2019.
- ^ Ливио, Марио (ноябрь 2002 г.). "Золотое сечение и эстетика" . Получено 26 июня 2015 г.
Внешние ссылки
- Конференция Bridges Organization, посвященная связям между искусством и математикой
- Преодолевая разрыв между математикой и искусством – слайд-шоу из Scientific American
- Открывая искусство математики
- Математика и искусство – AMS
- Математика и искусство – Cut-the-Knot
- Математическая образность – Американское математическое общество
- Математика в искусстве и архитектуре – Национальный университет Сингапура
- Математическое искусство – Виртуальный музей математики
- Когда искусство и математика сталкиваются – Science News
- Почему история математики — это также история искусства: Линн Гэмвелл в The Guardian







.jpg/440px-The_Arnolfini_Portrait,_détail_(2).jpg)





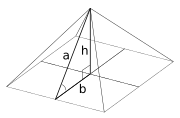




2.jpg/440px-Ming_flower_brocade_(cropped)2.jpg)






.jpg/440px-Mezquita_Shah,_Isfahán,_Irán,_2016-09-20,_DD_64_(detail).jpg)

![Туника инков Тупа из Перу, 1450–1540 гг., андская ткань, обозначающая высокий ранг[70]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a2/Tupa-inca-tunic.png/152px-Tupa-inca-tunic.png)













![Математическое оригами: Spring Into Action, Джеффа Бейнона, сделано из одного бумажного прямоугольника.[190]](http://upload.wikimedia.org/wikipedia/commons/thumb/9/9d/Origami_spring.jpg/440px-Origami_spring.jpg)





