Теория представления
Теория представлений — это раздел математики , который изучает абстрактные алгебраические структуры , представляя их элементы как линейные преобразования векторных пространств , и изучает модули над этими абстрактными алгебраическими структурами. [1] [2] По сути, представление делает абстрактный алгебраический объект более конкретным, описывая его элементы матрицами и их алгебраическими операциями (например, сложение матриц , умножение матриц ). Теория матриц и линейных операторов хорошо понятна, [3] поэтому представления более абстрактных объектов в терминах знакомых объектов линейной алгебры помогают почерпнуть свойства и иногда упростить вычисления в более абстрактных теориях.
Алгебраические объекты , поддающиеся такому описанию, включают группы , ассоциативные алгебры и алгебры Ли . Наиболее выдающейся из них (и исторически первой) является теория представлений групп , в которой элементы группы представляются обратимыми матрицами, такими, что групповая операция — матричное умножение. [4] [5]
Теория представлений является полезным методом, поскольку она сводит проблемы абстрактной алгебры к проблемам линейной алгебры , предмета, который хорошо изучен. [6] Например, представление группы бесконечномерным гильбертовым пространством позволяет применять методы анализа к теории групп. [7] [8] Кроме того, теория представлений важна в физике, поскольку она может описывать, как группа симметрии физической системы влияет на решения уравнений, описывающих эту систему. [9]
Теория представлений проникает во все области математики. Приложения теории представлений разнообразны. [10] Помимо своего влияния на алгебру, теория представлений
- обобщает анализ Фурье через гармонический анализ , [11]
- связана с геометрией через инвариантную теорию и программу Эрлангена , [12]
- оказывает влияние на теорию чисел посредством автоморфных форм и программы Ленглендса . [13]
Существуют различные подходы к теории представлений. Одни и те же объекты могут изучаться с использованием методов алгебраической геометрии , теории модулей , аналитической теории чисел , дифференциальной геометрии , теории операторов , алгебраической комбинаторики и топологии . [14]
Успех теории представлений привел к многочисленным обобщениям. Одно из самых общих — в теории категорий . [15] Алгебраические объекты, к которым применяется теория представлений, можно рассматривать как особые виды категорий, а представления — как функторы из категории объектов в категорию векторных пространств . [5] Это описание указывает на два очевидных обобщения: во-первых, алгебраические объекты можно заменить более общими категориями; во-вторых, целевая категория векторных пространств может быть заменена другими хорошо понятными категориями.
Определения и понятия
Пусть будет векторным пространством над полем . [6] Например, предположим, что есть или , стандартное n -мерное пространство векторов столбцов над действительными или комплексными числами , соответственно. В этом случае идея теории представлений заключается в том, чтобы делать абстрактную алгебру конкретно, используя матрицы действительных или комплексных чисел.
Существует три основных вида алгебраических объектов, для которых это можно сделать: группы , ассоциативные алгебры и алгебры Ли . [16] [5]
- Множество всех обратимых матриц является группой относительно умножения матриц , а теория представлений групп анализирует группу, описывая («представляя») ее элементы в терминах обратимых матриц.
- Сложение и умножение матриц превращают множество всех матриц в ассоциативную алгебру, и, следовательно, существует соответствующая теория представлений ассоциативных алгебр .
- Если заменить матричное умножение матричным коммутатором , то матрицы станут алгеброй Ли, что приведет к теории представлений алгебр Ли .
Это обобщается на любое поле и любое векторное пространство над , при этом линейные отображения заменяют матрицы, а композиция заменяет умножение матриц: существует группа автоморфизмов , ассоциативная алгебра всех эндоморфизмов и соответствующая алгебра Ли .
Определение
Действие
Существует два способа определения представления. [17] Первый использует идею действия , обобщая способ, которым матрицы действуют на векторы-столбцы посредством умножения матриц.
Представление группы или (ассоциативной или Ли) алгебры на векторном пространстве — это отображение с двумя свойствами.
- Для любого в (или в ) отображение линейно (по ).
- Если ввести обозначение g · v для ( g , v ), то для любых g 1 , g 2 из G и v из V : где e — единичный элемент группы G , а g 1 g 2 — групповое произведение в G .
Определение для ассоциативных алгебр аналогично, за исключением того, что ассоциативные алгебры не всегда имеют единичный элемент, в этом случае уравнение (2.1) опускается. Уравнение (2.2) является абстрактным выражением ассоциативности умножения матриц. Это не выполняется для матричного коммутатора, и для коммутатора также нет единичного элемента. Следовательно, для алгебр Ли единственным требованием является то, что для любых x 1 , x 2 в A и v в V : где [ x 1 , x 2 ] — скобка Ли , которая обобщает матричный коммутатор MN − NM .
Картографирование
Второй способ определения представления фокусируется на отображении φ, переводящем g в G в линейное отображение φ ( g ): V → V , которое удовлетворяет условию
и аналогично в других случаях. Этот подход является и более кратким, и более абстрактным. С этой точки зрения:
- представление группы G на векторном пространстве V — это гомоморфизм групп φ : G → GL( V , F ); [8]
- представление ассоциативной алгебры A в векторном пространстве V — это гомоморфизм алгебр φ : A → End F ( V ); [8]
- Представление алгебры Ли в векторном пространстве — это гомоморфизм алгебры Ли .
Терминология
Вектор V называется пространством представления φ , а его размерность (если она конечна) называется размерностью представления (иногда степенью , как в [18] ). Также общепринятой практикой является ссылка на само V как на представление, когда гомоморфизм φ ясен из контекста; в противном случае для обозначения представления можно использовать обозначение ( V , φ ).
Когда V имеет конечную размерность n , можно выбрать базис для V, чтобы отождествить V с F n и, следовательно, восстановить матричное представление с записями в поле F .
Эффективное или точное представление — это представление ( V , φ ), для которого гомоморфизм φ является инъективным .
Эквивариантные отображения и изоморфизмы
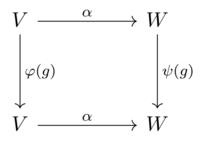
Если V и W — векторные пространства над F , снабженные представлениями φ и ψ группы G , то эквивариантное отображение из V в W — это линейное отображение α : V → W такое, что
для всех g в G и v в V. В терминах φ : G → GL( V ) и ψ : G → GL( W ) это означает
для всех g в G , то есть следующая диаграмма коммутирует :
Эквивариантные отображения для представлений ассоциативной или алгебры Ли определяются аналогично. Если α обратимо, то говорят, что это изоморфизм , в этом случае V и W (или, точнее, φ и ψ ) являются изоморфными представлениями , также называемыми эквивалентными представлениями . Эквивариантное отображение часто называют переплетающим отображением представлений. Кроме того, в случае группы G его иногда называют G -отображением.
Изоморфные представления, для практических целей, «одинаковы»; они предоставляют одинаковую информацию о представляемой группе или алгебре. Поэтому теория представлений стремится классифицировать представления с точностью до изоморфизма .
Подпредставления, частные и неприводимые представления
Если — представление (скажем) группы , и — линейное подпространство , которое сохраняется действием в том смысле, что для всех и , ( Серр называет их стабильными в [18] ), то называется подпредставлением : определяя, где — ограничение на , — представление , а включение — эквивариантное отображение. Фактор-пространство также можно превратить в представление . Если имеет ровно два подпредставления, а именно тривиальное подпространство {0} и себя, то представление называется неприводимым ; если имеет собственное нетривиальное подпредставление, то представление называется приводимым . [ 19]
Определение неприводимого представления подразумевает лемму Шура : эквивариантное отображение между неприводимыми представлениями является либо нулевым отображением , либо изоморфизмом, поскольку его ядро и образ являются подпредставлениями. В частности, когда , это показывает, что эквивариантные эндоморфизмы образуют ассоциативную алгебру с делением над базовым полем F . Если F алгебраически замкнуто , единственными эквивариантными эндоморфизмами неприводимого представления являются скалярные кратные единицы.
Неприводимые представления являются строительными блоками теории представлений для многих групп: если представление не является неприводимым, то оно построено из подпредставления и фактора, которые оба являются «более простыми» в некотором смысле; например, если является конечномерным, то и подпредставление, и фактор имеют меньшую размерность. Существуют контрпримеры, когда представление имеет подпредставление, но имеет только один нетривиальный неприводимый компонент. Например, аддитивная группа имеет двумерное представление Эта группа имеет вектор, фиксированный этим гомоморфизмом, но дополнительное подпространство отображается в , давая только одно неприводимое подпредставление. Это верно для всех унипотентных групп . [20] : 112
Прямые суммы и неразложимые представления
Если ( V , φ ) и ( W , ψ ) являются представлениями (скажем) группы G , то прямая сумма V и W является представлением, каноническим образом, посредством уравнения
Прямая сумма двух представлений несет не больше информации о группе G , чем два представления по отдельности. Если представление является прямой суммой двух собственных нетривиальных подпредставлений, оно называется разложимым. В противном случае оно называется неразложимым.
Полная сводимость
При благоприятных обстоятельствах каждое конечномерное представление является прямой суммой неприводимых представлений: такие представления называются полупростыми . В этом случае достаточно понимать только неприводимые представления. Примерами, где встречается это явление « полной приводимости », являются конечные группы (см. теорему Машке ), компактные группы и полупростые алгебры Ли.
В случаях, когда полная сводимость не выполняется, необходимо понимать, как неразложимые представления могут быть построены из неприводимых представлений как расширения фактора по подпредставлению.
Тензорные произведения представлений
Предположим, что и являются представлениями группы . Тогда мы можем сформировать представление G, действующее на векторном пространстве тензорного произведения , следующим образом: [21]
- .
Если и являются представлениями алгебры Ли, то правильной формулой для использования является [22]
- .
Это произведение можно распознать как копроизведение на коалгебре . В общем случае тензорное произведение неприводимых представлений не является неприводимым; процесс разложения тензорного произведения в прямую сумму неприводимых представлений известен как теория Клебша–Гордана .
В случае теории представлений группы SU(2) (или, что эквивалентно, ее комплексифицированной алгебры Ли ) разложение легко выполнить. [23] Неприводимые представления помечаются параметром , который является неотрицательным целым числом или полуцелым числом; тогда представление имеет размерность . Предположим, что мы берем тензорное произведение представления двух представлений с метками и , где мы предполагаем . Тогда тензорное произведение разлагается как прямая сумма одной копии каждого представления с меткой , где изменяется от до с шагом 1. Если, например, , то значениями , которые встречаются, являются 0, 1 и 2. Таким образом, представление тензорного произведения размерности разлагается как прямая сумма одномерного представления, трехмерного представления и пятимерного представления .
Ветви и темы
Теория представлений примечательна количеством своих ветвей и разнообразием подходов к изучению представлений групп и алгебр. Хотя все теории имеют общие основные концепции, которые уже обсуждались, они значительно различаются в деталях. Различия как минимум в 3 раза:
- Теория представления зависит от типа представляемого алгебраического объекта. Существует несколько различных классов групп, ассоциативных алгебр и алгебр Ли, и их теории представления имеют индивидуальный оттенок.
- Теория представлений зависит от природы векторного пространства, на котором представлен алгебраический объект. Наиболее важное различие — между конечномерными и бесконечномерными представлениями. В бесконечномерном случае важны дополнительные структуры (например, является ли пространство гильбертовым пространством , банаховым пространством и т. д.). Дополнительные алгебраические структуры могут быть также наложены в конечномерном случае.
- Теория представлений зависит от типа поля , над которым определено векторное пространство. Наиболее важными случаями являются поле комплексных чисел, поле действительных чисел, конечные поля и поля p-адических чисел . Дополнительные трудности возникают для полей положительной характеристики и для полей, которые не являются алгебраически замкнутыми .
Конечные группы
Представления групп являются очень важным инструментом в изучении конечных групп. [24] Они также возникают в приложениях теории конечных групп к геометрии и кристаллографии . [25] Представления конечных групп демонстрируют многие черты общей теории и указывают путь к другим разделам и темам в теории представлений.
Над полем характеристики ноль представление конечной группы G обладает рядом удобных свойств. Во-первых, представления G полупросты (полностью приводимы). Это следствие теоремы Машке , которая утверждает, что любое подпредставление V G -представления W имеет G -инвариантное дополнение. Одно доказательство состоит в том, чтобы выбрать любую проекцию π из W в V и заменить ее ее средним π G, определяемым формулой
π G эквивариантен, а его ядро является требуемым дополнением.
Конечномерные G -представления можно понять с помощью теории характеров : характер представления φ : G → GL( V ) — это классовая функция χ φ : G → F, определяемая соотношением
где — след . Неприводимое представление группы G полностью определяется ее характером.
Теорема Машке справедлива в более общем случае для полей положительной характеристики p , таких как конечные поля , при условии, что простое число p взаимно просто с порядком G. Когда p и | G | имеют общий множитель , существуют G - представления , которые не являются полупростыми, и они изучаются в подветви, называемой модульной теорией представлений .
Методы усреднения также показывают, что если F — действительное или комплексное число, то любое G -представление сохраняет скалярное произведение на V в том смысле, что
для всех g в G и v , w в W. Следовательно, любое G -представление унитарно .
Унитарные представления автоматически полупросты, поскольку результат Машке может быть доказан путем взятия ортогонального дополнения подпредставления. При изучении представлений групп, которые не являются конечными, унитарные представления обеспечивают хорошее обобщение действительных и комплексных представлений конечной группы.
Результаты, такие как теорема Машке и унитарное свойство, которые опираются на усреднение, могут быть обобщены на более общие группы путем замены среднего на интеграл, при условии, что можно определить подходящее понятие интеграла. Это можно сделать для компактных топологических групп (включая компактные группы Ли), используя меру Хаара , и полученная теория известна как абстрактный гармонический анализ .
Над произвольными полями другим классом конечных групп, которые имеют хорошую теорию представлений, являются конечные группы типа Ли . Важными примерами являются линейные алгебраические группы над конечными полями. Теория представлений линейных алгебраических групп и групп Ли расширяет эти примеры до бесконечномерных групп, причем последние тесно связаны с представлениями алгебр Ли . Важность теории характеров для конечных групп имеет аналог в теории весов для представлений групп Ли и алгебр Ли.
Представления конечной группы G также напрямую связаны с представлениями алгебры через групповую алгебру F [ G ], которая является векторным пространством над F с элементами G в качестве базиса, снабженным операцией умножения, определяемой групповой операцией, линейностью и требованием, чтобы групповая операция и скалярное умножение коммутировали.
Модульные представления
Модулярные представления конечной группы G являются представлениями над полем, характеристика которого не является взаимно простой с | G |, так что теорема Машке больше не верна (потому что | G | необратима в F , и поэтому на нее нельзя делить). [26] Тем не менее, Ричард Брауэр распространил большую часть теории характеров на модулярные представления, и эта теория сыграла важную роль в раннем прогрессе в направлении классификации конечных простых групп , особенно для простых групп, характеризация которых не поддавалась чисто групповым теоретико-групповым методам, поскольку их силовские 2-подгруппы были «слишком малы». [27]
Помимо приложений к теории групп, модулярные представления естественным образом возникают в других разделах математики , таких как алгебраическая геометрия , теория кодирования , комбинаторика и теория чисел .
Унитарные представления
Унитарное представление группы G — это линейное представление φ группы G на действительном или (обычно) комплексном гильбертовом пространстве V, такое, что φ ( g ) является унитарным оператором для любого g ∈ G . Такие представления широко применялись в квантовой механике с 1920-х годов, в частности, благодаря влиянию Германа Вейля [ 28] , и это вдохновило развитие теории, в частности, через анализ представлений группы Пуанкаре Юджином Вигнером [29] Одним из пионеров в построении общей теории унитарных представлений (для любой группы G, а не только для конкретных групп, полезных в приложениях) был Джордж Макки , а обширная теория была разработана Хариш-Чандрой и другими в 1950-х и 1960-х годах [30]
Основная цель — описать « унитарное дуальное », пространство неприводимых унитарных представлений группы G. [ 31] Теория наиболее хорошо развита в случае, когда G — локально компактная (хаусдорфова) топологическая группа , а представления сильно непрерывны . [11] Для абелевой группы G унитарное дуальное — это просто пространство характеров , тогда как для компактной группы G теорема Петера–Вейля показывает, что неприводимые унитарные представления конечномерны, а унитарное дуальное — дискретно. [32] Например, если G — группа окружности S 1 , то характеры задаются целыми числами, а унитарное дуальное — это Z .
Для некомпактного G вопрос о том, какие представления являются унитарными, является тонким. Хотя неприводимые унитарные представления должны быть «допустимыми» (как модули Хариш-Чандры ) и легко обнаружить, какие допустимые представления имеют невырожденную инвариантную полуторалинейную форму , трудно определить, когда эта форма является положительно определенной. Эффективное описание унитарного дуального, даже для относительно хорошо себя ведущих групп, таких как действительные редуктивные группы Ли (обсуждаемые ниже), остается важной открытой проблемой в теории представлений. Она была решена для многих конкретных групп, таких как SL(2, R ) и группа Лоренца . [33]
Гармонический анализ
Двойственность между группой окружности S 1 и целыми числами Z , или, в более общем смысле, между тором T n и Z n хорошо известна в анализе как теория рядов Фурье , а преобразование Фурье аналогичным образом выражает тот факт, что пространство символов на действительном векторном пространстве является дуальным векторным пространством . Таким образом, унитарная теория представления и гармонический анализ тесно связаны, и абстрактный гармонический анализ использует эту связь, развивая анализ функций на локально компактных топологических группах и связанных пространствах. [11]
Основная цель — предоставить общую форму преобразования Фурье и теоремы Планшереля . Это делается путем построения меры на унитарном дуальном и изоморфизма между регулярным представлением G на пространстве L 2 ( G ) квадратично интегрируемых функций на G и его представлением на пространстве функций L 2 на унитарном дуальном. Двойственность Понтрягина и теорема Петера–Вейля достигают этого для абелева и компактного G соответственно. [32] [ 34]
Другой подход предполагает рассмотрение всех унитарных представлений, а не только неприводимых. Они образуют категорию , и двойственность Таннаки–Крейна обеспечивает способ восстановления компактной группы из ее категории унитарных представлений.
Если группа не является ни абелевой, ни компактной, то неизвестна общая теория с аналогом теоремы Планшереля или обращения Фурье, хотя Александр Гротендик распространил двойственность Таннаки–Крейна на связь между линейными алгебраическими группами и таннакианскими категориями .
Гармонический анализ также был расширен с анализа функций на группе G до функций на однородных пространствах для G. Теория особенно хорошо развита для симметричных пространств и предоставляет теорию автоморфных форм (обсуждается ниже).
Группы Ли
| Lie groups and Lie algebras |
|---|
 |
Группа Ли — это группа, которая также является гладким многообразием . Многие классические группы матриц над действительными или комплексными числами являются группами Ли. [35] Многие из групп, важных в физике и химии, являются группами Ли, и их теория представлений имеет решающее значение для применения теории групп в этих областях. [9]
Теория представлений групп Ли может быть разработана сначала путем рассмотрения компактных групп, к которым применимы результаты теории компактных представлений. [31] Эта теория может быть расширена до конечномерных представлений полупростых групп Ли с помощью унитарного трюка Вейля : каждая полупростая вещественная группа Ли G имеет комплексификацию, которая является комплексной группой Ли G c , и эта комплексная группа Ли имеет максимальную компактную подгруппу K . Конечномерные представления G близко соответствуют представлениям K .
Общая группа Ли является полупрямым произведением разрешимой группы Ли и полупростой группы Ли ( разложение Леви ). [36] Классификация представлений разрешимых групп Ли в общем случае неразрешима, но часто проста в практических случаях. Представления полупрямых произведений затем могут быть проанализированы с помощью общих результатов, называемых теорией Макки , которая является обобщением методов, используемых в классификации Вигнера представлений группы Пуанкаре.
Алгебры Ли
Алгебра Ли над полем F — это векторное пространство над F, снабженное кососимметричной билинейной операцией, называемой скобкой Ли , которая удовлетворяет тождеству Якоби . Алгебры Ли возникают, в частности, как касательные пространства к группам Ли в единичном элементе , что приводит к их интерпретации как «инфинитезимальных симметрий». [36] Важным подходом к теории представлений групп Ли является изучение соответствующей теории представлений алгебр Ли, но представления алгебр Ли также имеют внутренний интерес. [37]
Алгебры Ли, как и группы Ли, имеют разложение Леви на полупростые и разрешимые части, причем теория представлений разрешимых алгебр Ли в общем случае неразрешима. Напротив, конечномерные представления полупростых алгебр Ли полностью поняты после работы Эли Картана . Представление полупростой алгебры Ли 𝖌 анализируется путем выбора подалгебры Картана , которая по сути является общей максимальной подалгеброй 𝖍 𝖌, на которой скобка Ли равна нулю («абелева»). Представление 𝖌 можно разложить на весовые пространства , которые являются собственными пространствами для действия 𝖍 и инфинитезимального аналога характеров. Структура полупростых алгебр Ли затем сводит анализ представлений к легко понимаемой комбинаторике возможных весов, которые могут возникнуть. [36]
Бесконечномерные алгебры Ли
Существует много классов бесконечномерных алгебр Ли, представления которых были изучены. Среди них важным классом являются алгебры Каца–Муди. [38] Они названы в честь Виктора Каца и Роберта Муди , которые независимо друг от друга их открыли. Эти алгебры образуют обобщение конечномерных полупростых алгебр Ли и разделяют многие из их комбинаторных свойств. Это означает, что у них есть класс представлений, которые можно понимать так же, как представления полупростых алгебр Ли.
Аффинные алгебры Ли являются частным случаем алгебр Каца–Муди, которые имеют особое значение в математике и теоретической физике , особенно в конформной теории поля и теории точно решаемых моделей . Кац открыл элегантное доказательство некоторых комбинаторных тождеств, тождеств Макдональда , которое основано на теории представлений аффинных алгебр Каца–Муди.
Супералгебры Ли
Супералгебры Ли являются обобщениями алгебр Ли, в которых базовое векторное пространство имеет Z 2 -градуировку, а кососимметричность и свойства тождества Якоби скобки Ли изменяются знаками. Их теория представления аналогична теории представления алгебр Ли. [39]
Линейные алгебраические группы
Линейные алгебраические группы (или, в более общем смысле, аффинные групповые схемы ) являются аналогами в алгебраической геометрии групп Ли , но над более общими полями, чем просто R или C. В частности, над конечными полями они порождают конечные группы типа Ли . Хотя линейные алгебраические группы имеют классификацию, которая очень похожа на классификацию групп Ли, их теория представления довольно сильно отличается (и гораздо менее понятна) и требует других методов, поскольку топология Зарисского относительно слаба, а методы анализа больше не доступны. [40]
Теория инвариантов
Теория инвариантов изучает действия на алгебраических многообразиях с точки зрения их влияния на функции, которые образуют представления группы. Классически теория занималась вопросом явного описания полиномиальных функций , которые не изменяются или инвариантны относительно преобразований из заданной линейной группы . Современный подход анализирует разложение этих представлений на неприводимые. [41]
Теория инвариантов бесконечных групп неразрывно связана с развитием линейной алгебры , особенно с теориями квадратичных форм и определителей . Другим предметом с сильным взаимным влиянием является проективная геометрия , где теория инвариантов может быть использована для организации предмета, и в 1960-х годах Дэвид Мамфорд вдохнул в этот предмет новую жизнь в форме своей геометрической теории инвариантов . [42]
Теория представлений полупростых групп Ли берет свое начало в теории инвариантов [35] , а прочные связи между теорией представлений и алгебраической геометрией имеют много параллелей в дифференциальной геометрии, начиная с Эрлангенской программы Феликса Клейна и связей Эли Картана , которые помещают группы и симметрию в основу геометрии. [43] Современные разработки связывают теорию представлений и теорию инвариантов с такими разнообразными областями, как голономия , дифференциальные операторы и теория многих комплексных переменных .
Автоморфные формы и теория чисел
Автоморфные формы являются обобщением модулярных форм на более общие аналитические функции , возможно, нескольких комплексных переменных , с аналогичными свойствами преобразования. [44] Обобщение включает замену модулярной группы PSL 2 ( R ) и выбранной подгруппы конгруэнции полупростой группой Ли G и дискретной подгруппой Γ . Так же, как модулярные формы можно рассматривать как дифференциальные формы на факторе верхнего полупространства H = PSL 2 ( R )/SO(2), автоморфные формы можно рассматривать как дифференциальные формы (или подобные объекты) на Γ \ G / K , где K (обычно) является максимальной компактной подгруппой G . Однако требуется некоторая осторожность, поскольку фактор обычно имеет особенности. Фактор полупростой группы Ли по компактной подгруппе является симметричным пространством , и поэтому теория автоморфных форм тесно связана с гармоническим анализом на симметричных пространствах.
До разработки общей теории были подробно проработаны многие важные частные случаи, включая модулярные формы Гильберта и модулярные формы Зигеля . Важные результаты в теории включают формулу следа Сельберга и реализацию Робертом Ленглендсом того, что теорема Римана–Роха может быть применена для вычисления размерности пространства автоморфных форм. Последующее понятие «автоморфного представления» оказалось очень ценным для работы со случаем, когда G является алгебраической группой , рассматриваемой как адельная алгебраическая группа . В результате целая философия, программа Ленглендса, развилась вокруг связи между представлением и теоретико-числовыми свойствами автоморфных форм. [45]
Ассоциативные алгебры
В каком-то смысле представления ассоциативной алгебры обобщают как представления групп, так и алгебр Ли. Представление группы индуцирует представление соответствующего группового кольца или групповой алгебры , в то время как представления алгебры Ли взаимно однозначно соответствуют представлениям ее универсальной обертывающей алгебры . Однако теория представлений общих ассоциативных алгебр не обладает всеми хорошими свойствами теории представлений групп и алгебр Ли.
Теория модулей
При рассмотрении представлений ассоциативной алгебры можно забыть о базовом поле и просто рассматривать ассоциативную алгебру как кольцо, а ее представления как модули. Такой подход на удивление плодотворен: многие результаты в теории представлений можно интерпретировать как частные случаи результатов о модулях над кольцом.
Алгебры Хопфа и квантовые группы
Алгебры Хопфа предоставляют способ улучшить теорию представлений ассоциативных алгебр, сохраняя теорию представлений групп и алгебр Ли как частные случаи. В частности, тензорное произведение двух представлений является представлением, как и дуальное векторное пространство.
Алгебры Хопфа, связанные с группами, имеют коммутативную алгебраическую структуру, и поэтому общие алгебры Хопфа известны как квантовые группы , хотя этот термин часто ограничивается определенными алгебрами Хопфа, возникающими как деформации групп или их универсальных обертывающих алгебр. Теория представлений квантовых групп добавила удивительные идеи к теории представлений групп Ли и алгебр Ли, например, через кристаллический базис Кашивары.
Обобщения
Теоретико-множественные представления
Теоретико -множественное представление (также известное как представление группового действия или перестановочное представление ) группы G на множестве X задается функцией ρ из G в X X , множеством функций из X в X , таким, что для всех g 1 , g 2 из G и всех x из X :
Это условие и аксиомы для группы подразумевают, что ρ ( g ) является биекцией (или перестановкой ) для всех g в G. Таким образом , мы можем эквивалентно определить представление перестановки как гомоморфизм группы из G в симметрическую группу S X группы X.
Представления в других категориях
Каждая группа G может рассматриваться как категория с одним объектом; морфизмы в этой категории являются просто элементами G. Если задана произвольная категория C , представление G в C является функтором из G в C. Такой функтор выбирает объект X в C и групповой гомоморфизм из G в Aut( X ), группу автоморфизмов X .
В случае, когда C — это Vect F , категория векторных пространств над полем F , это определение эквивалентно линейному представлению. Аналогично, теоретико-множественное представление — это просто представление G в категории множеств .
В качестве другого примера рассмотрим категорию топологических пространств Top . Представления в Top являются гомоморфизмами из G в группу гомеоморфизмов топологического пространства X.
С линейными представлениями тесно связаны три типа представлений:
- проективные представления : в категории проективных пространств . Их можно описать как «линейные представления с точностью до скалярных преобразований».
- аффинные представления : в категории аффинных пространств . Например, евклидова группа действует аффинно на евклидовом пространстве .
- копредставления унитарных и антиунитарных групп : в категории комплексных векторных пространств с морфизмами, являющимися линейными или антилинейными преобразованиями.
Представления категорий
Поскольку группы являются категориями, можно также рассмотреть представление других категорий. Простейшее обобщение — моноиды , которые являются категориями с одним объектом. Группы — это моноиды, для которых каждый морфизм обратим. Общие моноиды имеют представления в любой категории. В категории множеств это действия моноидов , но можно изучать представления моноидов на векторных пространствах и других объектах.
В более общем смысле, можно ослабить предположение, что представляемая категория имеет только один объект. В полной общности это просто теория функторов между категориями, и мало что можно сказать.
Один особый случай оказал значительное влияние на теорию представлений, а именно на теорию представлений колчанов. [15] Колчан — это просто направленный граф (с разрешенными петлями и несколькими стрелками), но его можно превратить в категорию (а также в алгебру) путем рассмотрения путей в графе. Представления таких категорий/алгебр пролили свет на несколько аспектов теории представлений, например, позволяя в некоторых случаях сводить вопросы теории представлений, не относящиеся к полупростым, о группе, к вопросам теории представлений, относящимся к полупростым, о колчане.
Смотрите также
Примечания
- ^ Классические тексты по теории репрезентации включают Curtis & Reiner (1962) и Serre (1977). Другие превосходные источники — Fulton & Harris (1991) и Goodman & Wallach (1998).
- ^ "теория представлений в nLab". ncatlab.org . Получено 2019-12-09 .
- ^ Ронан, Марк Эндрю. "линейная алгебра". Encyclopedia Britannica . Получено 8 июля 2024 г. линейная
алгебра очень хорошо изучена
- ^ Об истории теории представлений конечных групп см. Lam (1998). Об алгебраических группах и группах Ли см. Borel (2001).
- ^ abc Этингоф, Павел; Гольберг, Олег; Хензель, Себастьян; Лю, Тянькай; Швенднер, Алекс; Вайнтроб, Дмитрий; Юдовина, Елена (10 января 2011 г.). "Введение в теорию представлений" (PDF) . www-math.mit.edu . Получено 09.12.2019 .
- ^ ab Существует множество учебников по векторным пространствам и линейной алгебре . Для более подробного изучения см. Kostrikin & Manin (1997).
- ↑ Салли и Воган 1989.
- ^ abc Телеман, Константин (2005). "Теория представлений" (PDF) . math.berkeley.edu . Получено 2019-12-09 .
- ^ ab Sternberg 1994.
- ^ Лэм 1998, стр. 372.
- ^ abc Фолланд 1995.
- ^ Гудман и Уоллах 1998, Олвер 1999, Шарп 1997.
- ^ Борель и Кассельман 1979, Гелбарт 1984.
- ^ См. предыдущие сноски, а также Бореля (2001).
- ^ Аб Симсон, Сковронски и Асем 2007.
- ^ Фултон и Харрис 1991, Симсон, Сковронски и Ассем 2007, Хамфрис 1972a.
- ^ Этот материал можно найти в стандартных учебниках, таких как Curtis & Reiner (1962), Fulton & Harris (1991), Goodman & Wallach (1998), James & Liebeck (1993), Humphreys (1972a), Jantzen (2003), Knapp (2001) и Serre (1977).
- ^ ab Serre 1977.
- ^ Представление {0} размерности ноль не считается ни приводимым, ни неприводимым, так же как число 1 не считается ни составным, ни простым .
- ^ Хамфрис, Джеймс Э. (1975). Линейные алгебраические группы. Нью-Йорк, Нью-Йорк: Springer New York. ISBN 978-1-4684-9443-3. OCLC 853255426.
- ^ Холл 2015 Раздел 4.3.2
- ^ Холл 2015 Предложение 4.18 и Определение 4.19
- ^ Холл 2015 Приложение C
- ^ Альперин 1986, Лам 1998, Серр 1977.
- ^ Ким 1999.
- ↑ Серр 1977, Часть III.
- ^ Альперин 1986.
- ↑ См. Вейль 1928.
- ↑ Вигнер 1939.
- ^ Борель 2001.
- ^ ab Knapp 2001.
- ^ Питер и Вейль, 1927.
- ^ Баргманн 1947.
- ↑ Понтрягин 1934.
- ^ ab Weyl 1946.
- ^ abc Фултон и Харрис 1991.
- ^ Хамфрис 1972a.
- ^ Кац 1990.
- ^ Кац 1977.
- ^ Хамфрис 1972b, Янцен 2003.
- ^ Олвер 1999.
- ^ Мамфорд, Фогарти и Кирван 1994.
- ^ Шарп 1997.
- ^ Борель и Кассельман 1979.
- ^ Гелбарт 1984.
Ссылки
- Альперин, Дж. Л. (1986), Теория локальных представлений: модулярные представления как введение в теорию локальных представлений конечных групп , Cambridge University Press, ISBN 978-0-521-44926-7.
- Баргманн, В. (1947), «Неприводимые унитарные представления группы Лоренца», Annals of Mathematics , 48 (3): 568–640, doi :10.2307/1969129, JSTOR 1969129.
- Борель, Арманд (2001), Очерки истории групп Ли и алгебраических групп , Американское математическое общество, ISBN 978-0-8218-0288-5.
- Борель, Арманд; Кассельман, В. (1979), Автоморфные формы, представления и L-функции , Американское математическое общество, ISBN 978-0-8218-1435-2.
- Кертис, Чарльз В .; Райнер, Ирвинг (1962), Теория представлений конечных групп и ассоциативных алгебр , John Wiley & Sons (переиздание 2006 г. AMS Bookstore), ISBN 978-0-470-18975-7.
- Фолланд, Джеральд Б. (1995), Курс абстрактного гармонического анализа , CRC Press, ISBN 978-0-8493-8490-5.
- Фултон, Уильям ; Харрис, Джо (1991). Теория представлений. Первый курс . Graduate Texts in Mathematics , Readings in Mathematics. Том 129. Нью-Йорк: Springer-Verlag. doi :10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103..
- Гелбарт, Стивен (1984), «Элементарное введение в программу Ленглендса», Бюллетень Американского математического общества , 10 (2): 177–219, doi : 10.1090/S0273-0979-1984-15237-6.
- Гудман, Роу; Уоллах, Нолан Р. (1998), Представления и инварианты классических групп , Cambridge University Press, ISBN 978-0-521-66348-9.
- Холл, Брайан С. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Graduate Texts in Mathematics, т. 222 (2-е изд.), Springer, ISBN 978-3319134666
- Хельгасон, Сигурдур (1978), Дифференциальная геометрия, группы Ли и симметричные пространства , Academic Press, ISBN 978-0-12-338460-7
- Хамфрис, Джеймс Э. (1972a), Введение в алгебры Ли и теорию представлений , Биркхойзер, ISBN 978-0-387-90053-7.
- Хамфрис, Джеймс Э. (1972b), Линейные алгебраические группы , Graduate Texts in Mathematics, т. 21, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-90108-4, МР 0396773
- Джеймс, Гордон; Либек, Мартин (1993), Представления и характеры групп , Кембридж: Cambridge University Press, ISBN 978-0-521-44590-0.
- Янцен, Йенс Карстен (2003), Представления алгебраических групп , Американское математическое общество, ISBN 978-0-8218-3527-2.
- Кац, Виктор Г. (1977), «Супералгебры Ли», Успехи в математике , 26 (1): 8–96, doi : 10.1016/0001-8708(77)90017-2.
- Кац, Виктор Г. (1990), Бесконечномерные алгебры Ли (3-е изд.), Cambridge University Press, ISBN 978-0-521-46693-6.
- Ким, Шун Кён (1999), Методы теории групп и их применение к молекулам и кристаллам: и применение к молекулам и кристаллам , Cambridge University Press, ISBN 978-0-521-64062-6.
- Кнапп, Энтони В. (2001), Теория представлений полупростых групп: обзор на основе примеров , Princeton University Press, ISBN 978-0-691-09089-4.
- Кострикин А.И. ; Манин, Юрий И. (1997), Линейная алгебра и геометрия , Тейлор и Фрэнсис, ISBN 978-90-5699-049-7.
- Лэм, TY (1998), «Представления конечных групп: сто лет», Notices of the AMS , 45 (3, 4): 361–372 (часть I), 465–474 (часть II).
- Любич, Юрий И. (1988). Введение в теорию банаховых представлений групп . Теория операторов: достижения и приложения. Т. 30. Базель: Birkhauser. ISBN 978-3-7643-2207-6.
- Мамфорд, Дэвид ; Фогарти, Дж.; Кирван, Ф. (1994), Геометрическая теория инвариантов , Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Результаты в математике и смежных областях (2)], vol. 34 (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-56963-3, МР 0214602; МР 0719371 (2-е изд.); МР 1304906(3-е изд.)
- Олвер, Питер Дж. (1999), Классическая теория инвариантов , Кембридж: Cambridge University Press, ISBN 978-0-521-55821-1.
- Питер, Ф.; Вейль, Герман (1927), «Die Vollständigkeit der примитивный Darstellungen einer geschlossenen kontinuierlichen Gruppe», Mathematische Annalen , 97 (1): 737–755, doi : 10.1007/BF01447892, S2CID 120013521.
- Понтрягин, Лев С. (1934), «Теория топологических коммутативных групп», Annals of Mathematics , 35 (2): 361–388, doi :10.2307/1968438, JSTOR 1968438.
- Салли, Пол ; Воган, Дэвид А. (1989), Теория представлений и гармонический анализ на полупростых группах Ли , Американское математическое общество, ISBN 978-0-8218-1526-7.
- Серр, Жан-Пьер (1977), Линейные представления конечных групп , Springer-Verlag, ISBN 978-0387901909.
- Шарп, Ричард В. (1997), Дифференциальная геометрия: обобщение Картаном программы Эрлангена Клейна , Springer, ISBN 978-0-387-94732-7.
- Симсон, Дэниел; Сковронски, Анджей; Ассем, Ибрагим (2007), Элементы теории представлений ассоциативных алгебр , Cambridge University Press, ISBN 978-0-521-88218-7.
- Стернберг, Шломо (1994), Теория групп и физика , Cambridge University Press, ISBN 978-0-521-55885-3.
- Tung, Wu-Ki (1985). Теория групп в физике (1-е изд.). Нью-Джерси·Лондон·Сингапур·Гонконг: World Scientific . ISBN 978-9971966577.
- Вейль, Герман (1928), Gruppentheorie und Quantenmechanik (Теория групп и квантовая механика, перевод HP Робертсона, изд. 1931 г.), С. Хирцель, Лейпциг (переиздано в 1950 г., Дувр), ISBN 978-0-486-60269-1.
- Вейль, Герман (1946), Классические группы: их инварианты и представления (2-е изд.), Princeton University Press (переиздано в 1997 г.), ISBN 978-0-691-05756-9.
- Вигнер, Юджин П. (1939), «Об унитарных представлениях неоднородной группы Лоренца», Annals of Mathematics , 40 (1): 149–204, Bibcode : 1939AnMat..40..149W, doi : 10.2307/1968551, JSTOR 1968551, S2CID 121773411.
Внешние ссылки
- «Теория представлений», Энциклопедия математики , EMS Press , 2001 [1994]
- Александр Кириллов-младший , Введение в группы Ли и алгебры Ли (2008). Учебник, предварительная версия в формате pdf, которую можно загрузить с домашней страницы автора.
- Кевин Хартнетт, (2020), статья о теории представлений в журнале Quanta



















![{\displaystyle (2.2')\quad x_{1}\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{1},x_{2}]\cdot v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10034674f6c5c157ed625ace2e5626b62950c83b)

















































![{\displaystyle \rho (1)[x]=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/120857e96706f618d4b481e02c9ace79e8a12a0f)
![{\displaystyle \rho (g_{1}g_{2})[x]=\rho (g_{1})[\rho (g_{2})[x]].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/debb023e3f5e4ff703726b78494d7cc8acad5391)
