Теория узлов


В топологии теория узлов — это изучение математических узлов . Хотя математический узел вдохновлён узлами , которые встречаются в повседневной жизни, такими как шнурки и верёвки, он отличается тем, что его концы соединены, поэтому его нельзя развязать, простейшим узлом является кольцо (или « расстегнутый узел »). На математическом языке узел — это вложение окружности в трёхмерное евклидово пространство , . Два математических узла эквивалентны, если один может быть преобразован в другой посредством деформации на себя (известной как окружающая изотопия ); эти преобразования соответствуют манипуляциям с завязанной нитью, которые не включают её разрезание или пропускание через себя.
Узлы можно описывать разными способами. Используя разные методы описания, можно получить более одного описания одного и того же узла. Например, распространенным методом описания узла является плоская диаграмма, называемая диаграммой узла, на которой любой узел можно изобразить многими разными способами. Поэтому фундаментальной проблемой в теории узлов является определение того, когда два описания представляют один и тот же узел.
Существует полное алгоритмическое решение этой проблемы, которое имеет неизвестную сложность . [1] На практике узлы часто различаются с помощью инварианта узла , «величины», которая остается той же при вычислении из разных описаний узла. Важные инварианты включают полиномы узлов , группы узлов и гиперболические инварианты.
Первоначальным мотивом основателей теории узлов было создание таблицы узлов и связей , которые являются узлами из нескольких компонентов, запутанных друг с другом. Более шести миллиардов узлов и связей были табулированы с начала теории узлов в 19 веке.
Чтобы получить более глубокое понимание, математики обобщили концепцию узла несколькими способами. Узлы можно рассматривать в других трехмерных пространствах и использовать объекты, отличные от окружностей; см. узел (математика) . Например, узел более высокой размерности — это n- мерная сфера, вложенная в ( n +2)-мерное евклидово пространство.
История

Археологи обнаружили, что завязывание узлов восходит к доисторическим временам. Помимо их использования, такого как запись информации и связывание предметов, узлы интересовали людей своей эстетикой и духовным символизмом. Узлы появляются в различных формах китайского искусства, датируемого несколькими веками до нашей эры (см. Китайское плетение узлов ). Бесконечный узел появляется в тибетском буддизме , в то время как кольца Борромео неоднократно появлялись в разных культурах, часто представляя силу в единстве. Кельтские монахи, создавшие Келлскую книгу, щедро украшали целые страницы замысловатыми кельтскими узлами .

Математическая теория узлов была впервые разработана в 1771 году Александром-Теофилем Вандермондом, который явно отметил важность топологических особенностей при обсуждении свойств узлов, связанных с геометрией положения. Математические исследования узлов начались в 19 веке с Карла Фридриха Гаусса , который определил связующий интеграл (Silver 2006). В 1860-х годах теория лорда Кельвина о том, что атомы являются узлами в эфире, привела к созданию Питером Гатри Тейтом первых таблиц узлов для полной классификации. В 1885 году Тейт опубликовал таблицу узлов с числом пересечений до десяти и то, что стало известно как гипотезы Тейта . Эта запись мотивировала ранних теоретиков узлов, но теория узлов в конечном итоге стала частью формирующегося предмета топологии .
Эти топологи в начале 20-го века — Макс Ден , Дж. В. Александер и другие — изучали узлы с точки зрения группы узлов и инвариантов из теории гомологии, таких как многочлен Александера . Это был основной подход к теории узлов, пока серия прорывов не преобразила этот предмет.
В конце 1970-х годов Уильям Терстон ввел гиперболическую геометрию в изучение узлов с помощью теоремы о гиперболизации . Было показано, что многие узлы являются гиперболическими узлами , что позволило использовать геометрию для определения новых, мощных инвариантов узлов . Открытие полинома Джонса Воганом Джонсом в 1984 году (Sossinsky 2002, стр. 71–89) и последующие вклады Эдварда Виттена , Максима Концевича и других выявили глубокие связи между теорией узлов и математическими методами в статистической механике и квантовой теории поля . С тех пор было изобретено множество инвариантов узлов с использованием сложных инструментов, таких как квантовые группы и гомологии Флоера .
В последние несколько десятилетий 20-го века ученые заинтересовались изучением физических узлов , чтобы понять явления образования узлов в ДНК и других полимерах. Теория узлов может быть использована для определения того, является ли молекула хиральной (имеет ли она «рукость») или нет (Simon 1986). Клубки , струны с обоими концами, были эффективно использованы при изучении действия топоизомеразы на ДНК (Flapan 2000). Теория узлов может иметь решающее значение при построении квантовых компьютеров с помощью модели топологических квантовых вычислений (Collins 2006).
Эквивалентность узлов
Узел создается, начиная с одномерного отрезка линии, оборачивая его вокруг себя произвольно, а затем соединяя два его свободных конца вместе, чтобы сформировать замкнутую петлю (Адамс 2004) (Соссински 2002). Проще говоря, мы можем сказать, что узел — это «простая замкнутая кривая» (см. Кривая ) — то есть: «почти» инъективная и непрерывная функция , с единственной «неинъективностью» . Топологи считают узлы и другие запутывания, такие как зацепления и косы , эквивалентными, если узел можно плавно перемещать, не пересекая себя, чтобы он совпадал с другим узлом.
Идея эквивалентности узлов заключается в том, чтобы дать точное определение того, когда два узла следует считать одинаковыми, даже если они расположены совершенно по-разному в пространстве. Формальное математическое определение заключается в том, что два узла эквивалентны, если существует гомеоморфизм , сохраняющий ориентацию, с .
Это определение эквивалентности узлов означает, что два узла эквивалентны, когда существует непрерывное семейство гомеоморфизмов пространства на себя, такое, что последний из них переносит первый узел на второй узел. (Подробнее: Два узла и эквивалентны , если существует непрерывное отображение, такое что a) для каждого отображение, переводящее в , является гомеоморфизмом на себя; b) для всех ; и c) . Такая функция известна как объемлющая изотопия .)
Эти два понятия эквивалентности узлов сходятся в точности относительно того, какие узлы эквивалентны: Два узла, которые эквивалентны в определении гомеоморфизма, сохраняющего ориентацию, также эквивалентны в определении изотопии окружающего пространства, поскольку любой гомеоморфизм, сохраняющий ориентацию, на себя является конечной стадией изотопии окружающего пространства, начинающейся с тождества. И наоборот, два узла, эквивалентные в определении изотопии окружающего пространства, также эквивалентны в определении гомеоморфизма, сохраняющего ориентацию, поскольку (конечная) стадия изотопии окружающего пространства должна быть гомеоморфизмом, сохраняющим ориентацию, переносящим один узел в другой.
Основная проблема теории узлов, проблема распознавания , заключается в определении эквивалентности двух узлов. Существуют алгоритмы для решения этой проблемы, первый из которых был предложен Вольфгангом Хакеном в конце 1960-х годов (Hass 1998). Тем не менее, эти алгоритмы могут быть чрезвычайно трудоемкими, и основной проблемой в теории является понимание того, насколько сложна эта проблема на самом деле (Hass 1998). Особый случай распознавания неразвязанного узла , называемый проблемой распутывания , представляет особый интерес (Hoste 2005). В феврале 2021 года Марк Лакенби анонсировал новый алгоритм распознавания неразвязанных узлов, который работает за квазиполиномиальное время . [2]
Схемы узлов

Полезный способ визуализации и манипулирования узлами — спроецировать узел на плоскость — представьте, что узел отбрасывает тень на стену. Небольшое изменение направления проекции гарантирует, что она будет один к одному, за исключением двойных точек, называемых пересечениями , где «тень» узла пересекает себя один раз поперечно (Рольфсен, 1976). На каждом пересечении, чтобы иметь возможность воссоздать исходный узел, необходимо отличать верхнюю нить от нижней. Это часто делается путем создания разрыва в нити, идущей под ней. Полученная диаграмма представляет собой погруженную плоскую кривую с дополнительными данными о том, какая нить находится над, а какая под каждым пересечением. (Эти диаграммы называются диаграммами узлов , когда они представляют узел , и диаграммами связей , когда они представляют связь .) Аналогично, заузленные поверхности в 4-пространстве могут быть связаны с погруженными поверхностями в 3-пространстве.
Редуцированная диаграмма — это диаграмма узла, в которой нет редуцируемых пересечений (также невозвратных или устранимых пересечений ) или в которой все редуцируемые пересечения были удалены. [3] [4] Лепестковая проекция — это тип проекции, в которой вместо образования двойных точек все нити узла встречаются в одной точке пересечения, соединенные с ней петлями, образующими невложенные «лепестки». [5]
Рейдемейстер движется
В 1927 году, работая с этой диаграммной формой узлов, Дж. В. Александер и Гарланд Бэрд Бриггс, и независимо Курт Рейдемейстер , продемонстрировали, что две диаграммы узлов, принадлежащие одному и тому же узлу, могут быть связаны последовательностью трех видов ходов на диаграмме, показанной ниже. Эти операции, теперь называемые ходами Рейдемейстера , таковы:
- Скручивайте и раскручивайте в любом направлении.
- Полностью перекиньте одну прядь через другую.
- Полностью переместите прядь над или под перекрестком.
  |  |
| Тип I | Тип II |
|---|---|
 | |
| Тип 3 | |
Доказательство того, что диаграммы эквивалентных узлов связаны движениями Рейдемейстера, основано на анализе того, что происходит при плоской проекции движения, переносящего один узел в другой. Движение можно организовать так, что почти все время проекция будет диаграммой узла, за исключением конечного числа случаев, когда происходит «событие» или «катастрофа», например, когда более двух нитей пересекаются в точке или несколько нитей становятся касательными в точке. Тщательный анализ покажет, что сложные события можно устранить, оставив только самые простые события: (1) образование или выпрямление «перегиба»; (2) две нити становятся касательными в точке и проходят через нее; и (3) три нити пересекаются в точке. Это как раз и есть движения Рейдемейстера (Sossinsky 2002, ch. 3) (Lickorish 1997, ch. 1).
Инварианты узлов

Франсуа Геритау, Сола Шлеймера и Генри Сегермана
Инвариант узла — это «количество», которое одинаково для эквивалентных узлов (Adams 2004) (Lickorish 1997) (Rolfsen 1976). Например, если инвариант вычисляется из диаграммы узла, он должен давать одинаковое значение для двух диаграмм узлов, представляющих эквивалентные узлы. Инвариант может принимать одинаковое значение на двух разных узлах, поэтому сам по себе может быть неспособен различать все узлы. Элементарный инвариант — это трехцветность .
«Классические» инварианты узлов включают группу узлов , которая является фундаментальной группой дополнения узла , и многочлен Александера , который может быть вычислен из инварианта Александера, модуля, построенного из бесконечного циклического покрытия дополнения узла (Lickorish 1997)(Rolfsen 1976). В конце 20-го века были открыты такие инварианты, как «квантовые» многочлены узлов, инварианты Васильева и гиперболические инварианты. Эти вышеупомянутые инварианты являются лишь вершиной айсберга современной теории узлов.
Узловые полиномы
Многочлен узла — это инвариант узла , который является многочленом . Известные примеры включают многочлен Джонса , многочлен Александера и многочлен Кауфмана . Вариант многочлена Александера, многочлен Александера–Конвея , является многочленом от переменной z с целыми коэффициентами (Lickorish 1997).
Полином Александера–Конвея на самом деле определяется в терминах связей , которые состоят из одного или нескольких узлов, запутанных друг с другом. Концепции, объясненные выше для узлов, например, диаграммы и движения Рейдемейстера, также справедливы для связей.
Рассмотрим ориентированную диаграмму связей, т.е. ту, в которой каждый компонент связи имеет предпочтительное направление, обозначенное стрелкой. Для заданного пересечения диаграммы, пусть будут ориентированными диаграммами связей, полученными в результате изменения диаграммы, как показано на рисунке:

Исходная диаграмма может быть либо , либо , в зависимости от выбранной конфигурации пересечения. Тогда полином Александера–Конвея, , рекурсивно определяется в соответствии с правилами:
- (где есть какая-нибудь схема развязывания узла )
Второе правило — это то, что часто называют отношением скейн . Чтобы проверить, что эти правила дают инвариант ориентированной связи, нужно определить, что многочлен не меняется при трех движениях Рейдемейстера. Многие важные многочлены узлов могут быть определены таким образом.
Ниже приведен пример типичного вычисления с использованием отношения скейн. Он вычисляет полином Александера–Конвея узла трилистник . Желтые пятна указывают, где применяется отношение.
дает неразвязанный узел и связь Хопфа . Применяя отношение к связи Хопфа, где указано,
дает деформируемую связь с 0 пересечениями (на самом деле это расцепление двух компонентов) и расцепление. Расцепление требует немного хитрости:
что подразумевает, что C (расцепление двух компонентов) = 0, поскольку первые два полинома принадлежат расцеплению и, следовательно, равны.
Сопоставив все это, мы увидим:
Поскольку полином Александера–Конвея является инвариантом узла, это показывает, что трилистник не эквивалентен трилистнику. Так что трилистник действительно «завязан».
- Левосторонний узел-трилистник.
- Правосторонний узел-трилистник.
На самом деле, существует два трилистника, называемые правым и левым трилистниками, которые являются зеркальными отражениями друг друга (возьмите схему трилистника, приведенную выше, и измените каждое пересечение на другое, чтобы получить зеркальное отражение). Они не эквивалентны друг другу, что означает, что они не амфихиральны. Это было показано Максом Деном до изобретения полиномов узлов, с использованием методов теории групп (Dehn 1914). Но полином Александера–Конвея каждого вида трилистника будет тем же самым, как можно увидеть, пройдя через вычисления выше с зеркальным отражением. Полином Джонса на самом деле может различать левые и правые трилистники (Lickorish 1997).
Гиперболические инварианты
Уильям Терстон доказал, что многие узлы являются гиперболическими узлами , что означает, что дополнение узла (т. е. множество точек 3-пространства, не лежащих на узле) допускает геометрическую структуру, в частности, гиперболическую геометрию . Гиперболическая структура зависит только от узла, поэтому любая величина, вычисленная из гиперболической структуры, является инвариантом узла (Адамс 2004).
Геометрия позволяет нам визуализировать, как выглядит внутренняя часть узла или дополнения связи, представляя лучи света, движущиеся по геодезическим геометриям. Примером может служить изображение дополнения колец Борромео . Обитатель этого дополнения связи смотрит на пространство из области около красного компонента. Шары на рисунке — это виды оробарных окрестностей связи. Утолщая связь стандартным способом, мы получаем оробарные окрестности компонентов связи. Несмотря на то, что граница окрестности представляет собой тор, при просмотре изнутри дополнения связи она выглядит как сфера. Каждый компонент связи показывает столько же сфер (одного цвета), сколько и бесконечно много световых лучей от наблюдателя к компоненту связи. Фундаментальный параллелограмм (который указан на рисунке) заполняет как по вертикали, так и по горизонтали и показывает, как бесконечно расширять узор сфер.
Этот шаблон, шаблон горибола, сам по себе является полезным инвариантом. Другие гиперболические инварианты включают форму фундаментального параллелограмма, длину кратчайшей геодезической и объем. Современные усилия по табулированию узлов и связей эффективно используют эти инварианты. Быстрые компьютеры и умные методы получения этих инвариантов делают вычисление этих инвариантов на практике простой задачей (Adams, Hildebrand & Weeks 1991).
Более высокие измерения
Узел в трех измерениях можно развязать, поместив его в четырехмерное пространство. Это делается путем изменения пересечений. Предположим, что одна нить находится позади другой, если смотреть с выбранной точки. Поднимите ее в четвертое измерение, чтобы не было никаких препятствий (передняя нить не имеет там компонента); затем сдвиньте ее вперед и опустите назад, теперь спереди. Аналогиями для плоскости были бы подъем нити с поверхности или удаление точки из внутренней части круга.
Фактически, в четырех измерениях любая непересекающаяся замкнутая петля одномерной струны эквивалентна неразвязанному узлу. Сначала «втолкнем» петлю в трехмерное подпространство, что всегда возможно, хотя и технически сложно объяснить.
Однако в классической теории узлов встречается четырехмерное пространство, и важной темой является изучение срезанных узлов и ленточных узлов . Известная открытая проблема спрашивает, является ли каждый срезанный узел также ленточным.
Завязывание сфер более высокого измерения
Поскольку топологически узел можно считать одномерной сферой, следующим обобщением будет рассмотрение двумерной сферы ( ), вложенной в четырехмерное евклидово пространство ( ). Такое вложение заузлено, если не существует гомеоморфизма на себя, переводящего вложенную двумерную сферу в стандартное «круглое» вложение двумерной сферы. Подвешенные узлы и закрученные узлы — два типичных семейства таких двумерных сферических узлов.
Математический прием, называемый «общее положение», подразумевает, что для заданной n -сферы в m -мерном евклидовом пространстве, если m достаточно велико (в зависимости от n ), сфера должна быть распутана. В общем случае кусочно-линейные n -сферы образуют узлы только в ( n + 2)-мерном пространстве (Zeeman 1963), хотя это больше не является требованием для гладко заузленных сфер. Фактически, существуют гладко заузленные -сферы в 6 k -мерном пространстве; например, существует гладко заузленная 3-сфера в (Haefliger 1962) (Levine 1965). Таким образом, коразмерность гладкого узла может быть сколь угодно большой, если не фиксировать размерность заузленной сферы; однако любая гладкая k -сфера, вложенная в с , является распутанной. Понятие узла имеет дальнейшие обобщения в математике, см.: Узел (математика) , изотопическая классификация вложений .
Каждый узел в n -сфере является звеном вещественно-алгебраического множества с изолированной особенностью в (Акбулут и Кинг, 1981).
N -узел - это единичный вложенный в . N -связь состоит из k -копий вложенного в , где k - натуральное число . Оба случая и хорошо изучены, как и случай . [6] [ 7]
Добавление узлов

Два узла можно добавить, разрезав оба узла и соединив пары концов. Операция называется суммой узлов или иногда связанной суммой или композицией двух узлов. Это можно формально определить следующим образом (Адамс 2004): рассмотрим плоскую проекцию каждого узла и предположим, что эти проекции не пересекаются. Найдите прямоугольник на плоскости, где одна пара противоположных сторон является дугами вдоль каждого узла, в то время как остальная часть прямоугольника не пересекается с узлами. Образуйте новый узел, удалив первую пару противоположных сторон и присоединив другую пару противоположных сторон. Результирующий узел является суммой исходных узлов. В зависимости от того, как это сделано, могут получиться два разных узла (но не больше). Эту неоднозначность в сумме можно устранить, рассматривая узлы как ориентированные , т. е. имеющие предпочтительное направление движения вдоль узла и требующие, чтобы дуги узлов в сумме были ориентированы в соответствии с ориентированной границей прямоугольника.
Сумма узлов ориентированных узлов коммутативна и ассоциативна . Узел является простым , если он нетривиален и не может быть записан как сумма узлов двух нетривиальных узлов. Узел, который может быть записан как такая сумма, является составным . Существует разложение на простые числа для узлов, аналогичное простым и составным числам (Шуберт, 1949). Для ориентированных узлов это разложение также уникально. Узлы более высоких размерностей также могут быть добавлены, но есть некоторые различия. Хотя вы не можете образовать тривиальный узел в трех измерениях, вы можете это сделать в более высоких измерениях, по крайней мере, когда вы рассматриваете гладкие узлы в коразмерности не менее 3.
Узлы также могут быть построены с использованием подхода топологии цепи . Это делается путем объединения базовых единиц, называемых мягкими контактами, с использованием пяти операций (Параллельный, Последовательный, Перекрестный, Согласованный и Суб). [8] [9] Подход применим также к открытым цепям и может быть расширен для включения так называемых жестких контактов.
Табулирование узлов
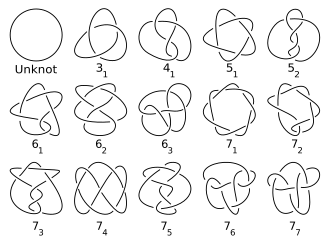
Традиционно узлы каталогизировались в терминах числа пересечений . Таблицы узлов обычно включают только простые узлы и только одну запись для узла и его зеркального отображения (даже если они различны) (Hoste, Thistlethwaite & Weeks 1998). Количество нетривиальных узлов с заданным числом пересечений быстро увеличивается, что делает табулирование вычислительно сложным (Hoste 2005, стр. 20). Попытки табулирования увенчались успехом в перечислении более 6 миллиардов узлов и связей (Hoste 2005, стр. 28). Последовательность количества простых узлов с заданным числом пересечений, вплоть до числа пересечений 16, такова: 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988,46 972 ,253 293 ,1 388 705 ... (последовательность A002863 в OEIS ). Хотя экспоненциальные верхняя и нижняя границы для этой последовательности известны, не было доказано, что эта последовательность строго возрастает (Адамс 2004).
Первые таблицы узлов Тейта, Литтла и Киркмана использовали диаграммы узлов, хотя Тейт также использовал предшественника нотации Доукера . Для узлов были изобретены различные нотации, которые позволяют более эффективно табулировать (Hoste 2005).
Ранние таблицы пытались перечислить все узлы с максимум 10 пересечениями и все чередующиеся узлы с 11 пересечениями (Hoste, Thistlethwaite & Weeks 1998). Развитие теории узлов благодаря Александеру, Рейдемейстеру, Сейферту и другим облегчило задачу проверки, и таблицы узлов до 9 пересечений включительно были опубликованы Александером–Бриггсом и Рейдемейстером в конце 1920-х годов.
Первая крупная проверка этой работы была сделана в 1960-х годах Джоном Хортоном Конвеем , который не только разработал новую нотацию, но и многочлен Александера–Конвея (Conway 1970) (Doll & Hoste 1991). Это подтвердило список узлов из не более чем 11 пересечений и новый список связей до 10 пересечений. Конвей нашел ряд пропусков, но только одно дублирование в таблицах Тейта–Литтла; однако он пропустил дубликаты, называемые парой Перко , которые были замечены только в 1974 году Кеннетом Перко (Perko 1974). Эта известная ошибка распространилась, когда Дейл Рольфсен добавил таблицу узлов в свой влиятельный текст, основанный на работе Конвея. Статья Конвея 1970 года по теории узлов также содержит типографское дублирование на странице с неальтернирующими 11-пересекающимися узлами и опускает 4 примера — 2 из них ранее были перечислены в дипломной работе Д. Ломбардеро в Принстоне в 1968 году, а еще 2 были впоследствии обнаружены Аленом Кодроном. [см. Perko (1982), Primality of certain knots, Topology Proceedings] Менее известен дубликат в его таблице из 10 перекрестных связей: 2.-2.-20.20 является зеркалом 8*-20:-20. [см. Perko (2016), Historical highlights of non-cyclic knot theory, J. Knot Theory Ramifications].
В конце 1990-х годов Хосте, Тистлтуэйт и Уикс составили таблицу всех узлов с 16 пересечениями (Хост, Тистлтуэйт и Уикс 1998). В 2003 году Ранкин, Флинт и Шерманн составили таблицу чередующихся узлов с 22 пересечениями (Хост 2005). В 2020 году Бертон составил таблицу всех простых узлов с 19 пересечениями (Бертон 2020).
Обозначение Александера–Бриггса
Это наиболее традиционная нотация, основанная на статье Джеймса В. Александра и Гарланда Б. Бриггса 1927 года и позднее расширенная Дейлом Рольфсеном в его таблице узлов (см. изображение выше и Список основных узлов ). Нотация просто организует узлы по их числу пересечений. Номер пересечения записывается с нижним индексом, чтобы обозначить его порядок среди всех узлов с этим числом пересечений. Этот порядок произволен и поэтому не имеет особого значения (хотя в каждом числе пересечений скрученный узел идет после торического узла ). Связи записываются с помощью номера пересечения с верхним индексом, чтобы обозначить число компонентов, и нижним индексом, чтобы обозначить его порядок среди связей с тем же числом компонентов и пересечений. Таким образом, узел трилистник записывается как 3 1 , а связь Хопфа — 22
1. Имена Александера–Бриггса в диапазоне от 10 162 до 10 166 неоднозначны из-за открытия пары Перко в исходных и последующих таблицах узлов Чарльза Ньютона Литтла , а также различий в подходах к исправлению этой ошибки в таблицах узлов и других публикациях, созданных после этого момента. [10]
Обозначение Доукера–Тислтуэйта

Нотация Доукера –Тислтуэйта , также называемая нотацией или кодом Доукера, для узла представляет собой конечную последовательность четных целых чисел. Числа генерируются путем следования за узлом и маркировки пересечений последовательными целыми числами. Поскольку каждое пересечение посещается дважды, это создает пару четных целых чисел с нечетными целыми числами. Соответствующий знак дается для обозначения пере- и недопересечения. Например, на этом рисунке диаграмма узла имеет пересечения, помеченные парами (1,6) (3,−12) (5,2) (7,8) (9,−4) и (11,−10). Нотация Доукера–Тислтуэйта для этой маркировки представляет собой последовательность: 6, −12, 2, 8, −4, −10. Диаграмма узла имеет более одной возможной нотации Даукера, и при реконструкции узла с помощью нотации Даукера–Тислтуэйта возникает хорошо понятная неоднозначность.
нотация Конвея
Нотация Конвея для узлов и связей, названная в честь Джона Хортона Конвея , основана на теории сплетений (Конвей 1970). Преимущество этой нотации в том, что она отражает некоторые свойства узла или связи.
Нотация описывает, как построить конкретную диаграмму связи связи. Начните с базового многогранника , 4-валентного связного плоского графа без двуугольных областей. Такой многогранник обозначается сначала числом вершин, а затем числом звездочек, которые определяют положение многогранника в списке базовых многогранников. Например, 10** обозначает второй 10-вершинный многогранник в списке Конвея.
Затем в каждую вершину подставляется алгебраический узел (каждая вершина ориентирована так, что нет произвольного выбора при подстановке). Каждый такой узел имеет обозначение, состоящее из цифр и знаков + или −.
Примером может служить 1*2 −3 2. 1* обозначает единственный базовый многогранник с 1 вершиной. 2 −3 2 — это последовательность, описывающая непрерывную дробь, связанную с рациональным клубком . Этот клубок вставляется в вершину базового многогранника 1*.
Более сложный пример: 8*3.1.2 0.1.1.1.1.1 Здесь снова 8* относится к базовому многограннику с 8 вершинами. Точки разделяют обозначения для каждого клубка.
Любая связь допускает такое описание, и очевидно, что это очень компактная запись даже для очень большого числа пересечений. Обычно используются и другие сокращения. Последний пример обычно записывается как 8*3:2 0, где единицы опускаются, а число точек сохраняется, за исключением точек в конце. Для алгебраического узла, такого как в первом примере, 1* часто опускается.
В новаторской статье Конвея по этой теме перечислены базовые многогранники с 10 вершинами, которые он использует для табулирования связей, ставших стандартными для этих связей. Для дальнейшего перечисления многогранников с большим числом вершин имеются нестандартные варианты.
код Гаусса
Код Гаусса , аналогичный обозначению Доукера–Тислтуэйта, представляет узел с последовательностью целых чисел. Однако вместо того, чтобы каждое пересечение было представлено двумя разными числами, пересечение помечено только одним числом. Когда пересечение является переходом, указывается положительное число. При переходе вниз — отрицательное число. Например, узел трилистник в коде Гаусса может быть задан как: 1,−2,3,−1,2,−3
Код Гаусса ограничен в своей способности определять узлы. Эта проблема частично решается с помощью расширенного кода Гаусса .
Смотрите также
- Список тем теории узлов
- Молекулярный узел
- Топология схемы
- Квантовая топология
- Теория лент
- Контактная геометрия#Лежандровы подмногообразия и узлы
- Узлы и графы
- Галстук § Узлы
- Трюк с ламповым шнуром
Ссылки
Источники
- Адамс, Колин (2004), Книга узлов: Элементарное введение в математическую теорию узлов , Американское математическое общество , ISBN 978-0-8218-3678-1
- Адамс, Колин; Кроуфорд, Томас; ДеМео, Бенджамин; Ландри, Майкл; Лин, Алекс Тонг; Монте, МерфиКейт; Парк, Соджон; Венкатеш, Сарасвати; Йи, Фарра (2015), «Проекции узлов с одним множественным пересечением», Журнал теории узлов и ее разветвлений , 24 (3): 1550011, 30, arXiv : 1208.5742 , doi : 10.1142/S021821651550011X, MR 3342136, S2CID 119320887
- Адамс, Колин; Хильдебранд, Мартин; Уикс, Джеффри (1991), «Гиперболические инварианты узлов и зацеплений», Труды Американского математического общества , 326 (1): 1–56, doi : 10.1090/s0002-9947-1991-0994161-2 , JSTOR 2001854
- Акбулут, Селман ; Кинг, Генри К. (1981), «Все узлы алгебраические», Comment. Math. Helv. , 56 (3): 339–351, doi :10.1007/BF02566217, S2CID 120218312
- Бар-Натан, Дрор (1995), «Об инвариантах узлов Васильева», Топология , 34 (2): 423–472, doi : 10.1016/0040-9383(95)93237-2
- Бертон, Бенджамин А. (2020). «Следующие 350 миллионов узлов». 36-й Международный симпозиум по вычислительной геометрии (SoCG 2020) . Лейбниц Междунар. Учеб. Информ. Том. 164. Schloss Dagstuhl-Leibniz-Zentrum für Informatik. стр. 25:1–25:17. doi : 10.4230/LIPIcs.SoCG.2020.25 .
- Коллинз, Грэм (апрель 2006 г.), «Вычисления с квантовыми узлами», Scientific American , 294 (4): 56–63, Bibcode : 2006SciAm.294d..56C, doi : 10.1038/scientificamerican0406-56, PMID 16596880
- Ден, Макс (1914), «Die beiden Kleeblattschlingen», Mathematische Annalen , 75 (3): 402–413, doi : 10.1007/BF01563732, S2CID 120452571
- Конвей, Джон Х. (1970), «Перечисление узлов и связей и некоторые их алгебраические свойства», Computational Problems in Abstract Algebra , Pergamon, стр. 329–358, doi :10.1016/B978-0-08-012975-4.50034-5, ISBN 978-0-08-012975-4
- Долл, Хельмут; Хосте, Джим (1991), «Таблица ориентированных связей. С приложением микрофиш», Math. Comp. , 57 (196): 747–761, Bibcode : 1991MaCom..57..747D, doi : 10.1090/S0025-5718-1991-1094946-4
- Флапан, Эрика (2000), Когда топология встречается с химией: топологический взгляд на молекулярную хиральность , Outlook, Cambridge University Press , ISBN 978-0-521-66254-3
- Хефлигер, Андре (1962), «Узловые (4 k − 1)-сферы в 6 k -пространстве», Annals of Mathematics , вторая серия, 75 (3): 452–466, doi :10.2307/1970208, JSTOR 1970208
- Хакен, Вольфганг (1962), «Über das Homöomorphieproblem der 3-Mannigfaltigkeiten. I», Mathematische Zeitschrift , 80 : 89–120, doi : 10.1007/BF01162369, ISSN 0025-5874, MR 0160196
- Хасс, Джоэл (1998), «Алгоритмы распознавания узлов и 3-многообразий», Хаос, солитоны и фракталы , 9 (4–5): 569–581, arXiv : math/9712269 , Bibcode : 1998CSF.....9..569H, doi : 10.1016/S0960-0779(97)00109-4, S2CID 7381505
- Хост, Джим; Тистлтуэйт, Морвен ; Уикс, Джеффри (1998), «Первые 1 701 935 узлов», Math. Intelligencer , 20 (4): 33–48, doi :10.1007/BF03025227, S2CID 18027155
- Hoste, Jim (2005). «Перечисление и классификация узлов и связей». Handbook of Knot Theory . С. 209–232. doi :10.1016/B978-044451452-3/50006-X. ISBN 978-0-444-51452-3.
- Левин, Джером (1965), «Классификация дифференцируемых узлов», Annals of Mathematics , вторая серия, 1982 (1): 15–50, doi :10.2307/1970561, JSTOR 1970561
- Концевич, М. (1993). «Инварианты узла Васильева». Семинар И.М. Гельфанда . АДВСОВ. Том. 16. С. 137–150. дои : 10.1090/advsov/016.2/04. ISBN 978-0-8218-4117-4.
- Ликориш, У. Б. Рэймонд (1997), Введение в теорию узлов, Graduate Texts in Mathematics, т. 175, Springer-Verlag, doi : 10.1007/978-1-4612-0691-0, ISBN 978-0-387-98254-0, S2CID 122824389
- Перко, Кеннет (1974), «О классификации узлов», Труды Американского математического общества , 45 (2): 262–6, doi : 10.2307/2040074 , JSTOR 2040074
- Рольфсен, Дейл (1976), Узлы и связи, серия лекций по математике, т. 7, Беркли, Калифорния : Publish or Perish, ISBN 978-0-914098-16-4, МР 0515288
- Шуберт, Хорст (1949). Die eindeutige Zerlegbarkeit eines Knotens in Primknoten . дои : 10.1007/978-3-642-45813-2. ISBN 978-3-540-01419-5.
- Сильвер, Дэниел (2006). «Странное происхождение теории узлов». American Scientist . 94 (2): 158. doi :10.1511/2006.2.158.
- Саймон, Джонатан (1986), «Топологическая хиральность некоторых молекул», Топология , 25 (2): 229–235, doi : 10.1016/0040-9383(86)90041-8
- Сосинский, Алексей (2002), Узлы, математика с изюминкой , Издательство Гарвардского университета, ISBN 978-0-674-00944-8
- Тураев, Владимир Г. (2016). Квантовые инварианты узлов и 3-многообразий . doi :10.1515/9783110435221. ISBN 978-3-11-043522-1. S2CID 118682559.
- Weisstein, Eric W. (2013). "Reduced Knot Diagram". MathWorld . Wolfram . Получено 8 мая 2013 г. .
- Weisstein, Eric W. (2013a). "Reducible Crossing". MathWorld . Wolfram . Получено 8 мая 2013 г. .
- Виттен, Эдвард (1989), «Квантовая теория поля и многочлен Джонса», Comm. Math. Phys. , 121 (3): 351–399, Bibcode : 1989CMaPh.121..351W, doi : 10.1007/BF01217730, S2CID 14951363
- Зееман, Эрик К. (1963), «Распутывание комбинаторных шаров», Annals of Mathematics , вторая серия, 78 (3): 501–526, doi :10.2307/1970538, JSTOR 1970538
Сноски
- ^ Как впервые набросал с использованием теории многообразий Хакена Хакен (1962). Для более позднего обзора см. Hass (1998)
- ^ Марк Лакенби анонсирует новый алгоритм распознавания неразветвленных узлов, работающий за квазиполиномиальное время, Математический институт Оксфордского университета , 2021-02-03 , получено 2021-02-03
- ^ Вайсштейн 2013.
- ^ Вайсштейн 2013а.
- ^ Адамс и др. 2015.
- ^ Левин, Дж.; Орр, К. (2000), «Обзор приложений хирургии к теории узлов и связей», Обзоры теории хирургии: статьи, посвященные CTC Wall , Анналы математических исследований, т. 1, Princeton University Press , CiteSeerX 10.1.1.64.4359 , ISBN 978-0691049380— Вводная статья по узлам и связям больших размеров для продвинутых читателей
- ^ Огаса, Эйдзи (2013), Введение в узлы больших размерностей , arXiv : 1304.6053 , Bibcode : 2013arXiv1304.6053O— Вводная статья по узлам и связям больших размеров для начинающих
- ^ Головнев, Анатолий; Машаги, Алиреза (7 декабря 2021 г.). «Топология цепей для проектирования молекулярных узлов снизу вверх». Симметрия . 13 (12): 2353. arXiv : 2106.03925 . Bibcode : 2021Symm...13.2353G. doi : 10.3390/sym13122353 .
- ^ Флапан, Эрика; Машаги, Алиреза; Вонг, Хелен (1 июня 2023 г.). «Плиточная модель топологии цепи самозапутанных биополимеров». Научные отчеты . 13 (1): 8889. Бибкод : 2023NatSR..13.8889F. дои : 10.1038/s41598-023-35771-8. ПМЦ 10235088 . ПМИД 37264056.
- ^ "Месть пары Перко", RichardElwes.co.uk . Доступно в феврале 2016 г. Ричард Элвес указывает на распространенную ошибку в описании пары Перко.
Дальнейшее чтение
Вводные учебники
Существует ряд вступлений в теорию узлов. Классическое введение для аспирантов или студентов старших курсов — (Rolfsen 1976). Другие хорошие тексты из списка литературы — (Adams 2004) и (Lickorish 1997). Adams неформальный и доступен в основном для старшеклассников. Lickorish — строгое введение для аспирантов, охватывающее хорошее сочетание классических и современных тем. (Cromwell 2004) подходит для студентов, которые знают топологию точек-множеств; знание алгебраической топологии не требуется.
- Бурде, Герхард; Цишанг, Хайнер (1985), Узлы, Исследования Де Грюйтера по математике, том. 5, Вальтер де Грюйтер, ISBN 978-3-11-008675-1
- Кроуэлл, Ричард Х.; Фокс, Ральф (1977). Введение в теорию узлов . Springer. ISBN 978-0-387-90272-2.
- Кауфман, Луис Х. (1987), Об узлах, Princeton University Press, ISBN 978-0-691-08435-0
- Кауфман, Луис Х. (2013), Узлы и физика (4-е изд.), World Scientific, ISBN 978-981-4383-00-4
- Кромвель, Питер Р. (2004), Узлы и связи, Cambridge University Press, ISBN 978-0-521-54831-1
Опросы
- Менаско, Уильям У.; Тистлтуэйт, Морвен , ред. (2005), Справочник по теории узлов , Elsevier, ISBN 978-0-444-51452-3
- В справочнике Менаско и Тистлтуэйта рассматривается ряд тем, имеющих отношение к современным тенденциям исследований, причем в доступной для студентов старших курсов форме, но представляющей интерес и для профессиональных исследователей.
- Ливио, Марио (2009), «Гл. 8: Необоснованная эффективность?», Является ли Бог математиком?, Simon & Schuster, стр. 203–218, ISBN 978-0-7432-9405-8
Внешние ссылки
- "Математика и узлы" Это онлайн-версия выставки, разработанной для "PopMath RoadShow" Королевского общества 1989 года. Ее целью было использование узлов для представления методов математики широкой публике.
История
- Томсон, сэр Уильям (1867), «О вихревых атомах», Труды Королевского общества Эдинбурга , VI : 94–105
- Силлиман, Роберт Х. (декабрь 1963 г.), «Уильям Томсон: Кольца дыма и атомизм девятнадцатого века», Isis , 54 (4): 461–474, doi : 10.1086/349764, JSTOR 228151, S2CID 144988108
- Фильм о современном воссоздании эксперимента Тейта с дымовыми кольцами
- История теории узлов (на домашней странице Эндрю Раницки )
Таблицы узлов и программное обеспечение
- KnotInfo: Таблица инвариантов узлов и ресурсы по теории узлов
- Атлас узлов — подробная информация об отдельных узлах в таблицах узлов.
- KnotPlot — программное обеспечение для исследования геометрических свойств узлов
- Knotscape — программа для создания изображений узлов
- Knutilus — онлайн-база данных и генератор изображений узлов
- KnotData.html — функция Wolfram Mathematica для исследования узлов
- Regina — программное обеспечение для низкоразмерной топологии с собственной поддержкой узлов и связей. Таблицы простых узлов с числом пересечений до 19



![{\displaystyle K\двоеточие [0,1]\to \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3527c328346ff511b17bd2fe2ae5f3504df3d2e9)







![{\displaystyle H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dc228092f3ea7de7bbd32a579a7498ea08e9fb2)
![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)






































