Равнобедренная фигура

В геометрии мозаика размерности 2 (плоская мозаика) или выше, или многогранник размерности 3 ( многогранник ) или выше является изоэдральной или гране-транзитивной , если все его грани одинаковы. Более конкретно, все грани должны быть не просто конгруэнтными , но и транзитивными , т. е. должны лежать в пределах одной и той же орбиты симметрии . Другими словами, для любых двух граней A и B должна быть симметрия всей фигуры относительно переносов , вращений и/или отражений , которая отображает A на B. По этой причине выпуклые изоэдральные многогранники являются формами, которые будут делать честные игральные кости . [1]
Равногранные многогранники называются изоэдрами . Их можно описать конфигурацией граней . Равногранник имеет четное число граней.
Двойственный многограннику изоэдральный многогранник вершинно-транзитивен , т. е. изогонален. Каталоновые тела , бипирамиды и трапецоэдры являются изоэдральными. Они являются двойственными (изогональным) архимедовым телам , призмам и антипризмам соответственно. Платоновы тела , которые являются либо самодвойственными, либо двойственными с другим Платоновым телом, вершинно-, рёберно- и гранно-транзитивны (т. е. изогональны, изотоксальны и изоэдральны).
Форма, которая является изоэдральной, имеет регулярные вершины и также является транзитивной по ребрам (т. е. изотоксальной), называется квазирегулярной дуальной. Некоторые теоретики считают эти фигуры истинно квазирегулярными, поскольку они разделяют те же симметрии, но это не является общепринятым.
Многогранник, который является равногранным и изогональным, называется благородным .
Не все изозоноэдры [2] являются изоэдрическими. [3] Например, ромбический икосаэдр является изозоноэдром, но не изоэдром. [4]
Примеры
| Выпуклый | Вогнутый | ||
|---|---|---|---|
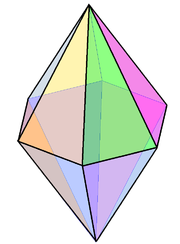 Шестиугольные бипирамиды , V4.4.6, представляют собой неправильные равногранные многогранники. |  Пятиугольная мозаика Каира , V3.3.4.3.4, является равногранной. |  Ромбические додекаэдрические соты являются изоэдрическими (и изохорными, и заполняющими пространство). |  Квадратная мозаика, искаженная в спиральную H-мозаику (топологически эквивалентную), по-прежнему является изоэдральной. |
Классы изоэдров по симметрии
| Лица | Конфигурация лица . | Сорт | Имя | Симметрия | Заказ | Выпуклый | Копланарный | Невыпуклый |
|---|---|---|---|---|---|---|---|---|
| 4 | В3 3 | Платонический | тетраэдр тетрагональный двуклиноид ромбический двуклиноид | Т д , [3,3], (*332) Д 2д , [2 + ,2], (2*) Д 2 , [2,2] + , (222) | 24 4 4 4 |    | ||
| 6 | В3 4 | Платонический | кубический тригональный трапецоэдр асимметричный тригональный трапецоэдр | О h , [4,3], (*432) D 3d , [2 + ,6] (2*3) D 3 [2,3] + , (223) | 48 12 12 6 |    | ||
| 8 | В4 3 | Платонический | октаэдр квадратная бипирамида ромбическая бипирамида квадратный скаленоэдр | О ч , [4,3], (*432) Д 4ч , [2,4], (*224) Д 2ч , [2,2], (*222) Д 2д , [2 + ,4], (2*2) | 48 16 8 8 |   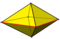    |  | |
| 12 | В3 5 | Платонический | правильный додекаэдр пиритоэдр тетратоид | Я ч , [5,3], (*532) Т ч , [3 + ,4], (3*2) Т, [3,3] + , (*332) | 120 24 12 |   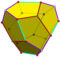 | 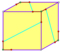 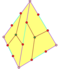 |   |
| 20 | В5 3 | Платонический | правильный икосаэдр | Я ч , [5,3], (*532) | 120 |  | ||
| 12 | В3.6 2 | каталонский | триакистетраэдр | Т д , [3,3], (*332) | 24 |  |   |  |
| 12 | В(3.4) 2 | каталонский | ромбический додекаэдр дельтовидный додекаэдр | О ч , [4,3], (*432) Т д , [3,3], (*332) | 48 24 |    |  |   |
| 24 | В3.8 2 | каталонский | триакисоктаэдр | О , [4,3], (*432 ) | 48 |  |   | |
| 24 | В4.6 2 | каталонский | тетракисгексаэдр | О , [4,3], (*432 ) | 48 |   |   |   |
| 24 | В3.4 3 | каталонский | дельтовидный икоситетраэдр | О , [4,3], (*432 ) | 48 |  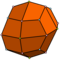 |    |  |
| 48 | В4.6.8 | каталонский | дисдьякис додекаэдр | О , [4,3], (*432 ) | 48 |  |    |   |
| 24 | В3 4 .4 | каталонский | пятиугольный икоситетраэдр | О, [4,3] + , (432) | 24 |  | ||
| 30 | В(3,5) 2 | каталонский | ромбический триаконтаэдр | Я ч , [5,3], (*532) | 120 |  | ||
| 60 | В3.10 2 | каталонский | триакисикосаэдр | Я ч , [5,3], (*532) | 120 |  |     | |
| 60 | В5.6 2 | каталонский | пентакисдодекаэдр | Я ч , [5,3], (*532) | 120 |  |      | |
| 60 | В3.4.5.4 | каталонский | дельтовидный гексаконтаэдр | Я ч , [5,3], (*532) | 120 |  |  |  |
| 120 | В4.6.10 | каталонский | дисдьякис триаконтаэдр | Я ч , [5,3], (*532) | 120 |  |    |    |
| 60 | В3 4 .5 | каталонский | пятиугольный гексаконтаэдр | Я, [5,3] + , (532) | 60 |  | ||
| 2 н | V3 3 . н | Полярный | трапецоэдр асимметричный трапецоэдр | D n d , [2 + ,2 n ], (2* n ) D n , [2, n ] + , (22 n ) | 4 н 2 н |   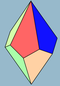    | ||
| 2 н 4 н | V4 2 . н V4 2 .2 н V4 2 .2 н | Полярный | правильная n - бипирамида изотоксальная 2 n -бипирамида 2 n - скаленоэдр | D н ч , [2, н ], (*22 н ) D н ч , [2, н ], (*22 н ) D нд , [2 + ,2 н ], (2* н ) | 4 н | 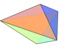    |        |
к-равногранныйфигура
Многогранник (или многогранник в общем случае) является k -изоэдральным , если он содержит k граней в пределах своих фундаментальных областей симметрии. [5] Аналогично, k -изоэдральная мозаика имеет k отдельных орбит симметрии (она может содержать m различных форм граней, для m = k или только для некоторых m < k ). [6] («1-изоэдральный» то же самое, что и «изоэдральный».)
Моноэдральный многогранник или моноэдральная мозаика ( m = 1) имеет конгруэнтные грани, либо прямо, либо зеркально, которые встречаются в одном или нескольких положениях симметрии. M - гранный многогранник или мозаика имеет m различных форм граней (« двугранный », « трехгранный »... то же самое, что «2-гранный», «3-гранный»... соответственно). [7]
Вот несколько примеров k -равногранных многогранников и мозаик, грани которых окрашены в соответствии с их k- симметрическими позициями:
| 3-равногранный | 4-равногранный | равногранный | 2-равногранный |
|---|---|---|---|
| 2-гранные правильногранные многогранники | Моноэдральные многогранники | ||
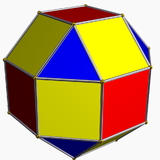 | 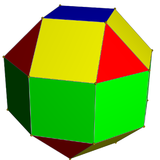 | 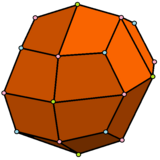 | 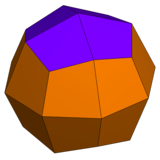 |
| Ромбикубооктаэдр имеет 1 треугольный тип и 2 квадратных типа. | Псевдоромбокубооктаэдр имеет 1 треугольный тип и 3 квадратных типа. | Дельтовидный икоситетраэдр имеет 1 тип грани. | Псевдодельтовидный икоситетраэдр имеет 2 типа граней одинаковой формы. |
| 2-равногранный | 4-равногранный | Изоэдрический | 3-равногранный |
|---|---|---|---|
| 2-гранные правильные мозаики | Моноэдральные мозаики | ||
 |  |  |  |
| Пифагорейская мозаика имеет 2 типа (размера) квадратов. | Эта 3-однородная мозаика имеет 3 типа треугольников одинаковой формы и 1 тип квадрата. | Узор «ёлочка» имеет 1 тип прямоугольника. | Эта пятиугольная мозаика состоит из 3 типов неправильных пятиугольников одинаковой формы. |
Связанные термины
Ячеечно -транзитивная или изохорная фигура — это n - политоп ( n ≥ 4) или n - сота ( n ≥ 3), ячейки которой конгруэнтны и транзитивны друг другу. В 3 измерениях катоптрические соты , двойственные однородным сотам, являются изохорными. В 4 измерениях изохорные многогранники были пронумерованы до 20 ячеек. [8]
Фасетно -транзитивная или изотопная фигура — это n -мерный многогранник или сота с конгруэнтными и транзитивными гранями (( n −1)- гранями ). Двойственный к изотопу многогранник — это изогональный многогранник. По определению, это изотопное свойство является общим для двойственных к однородным многогранникам многогранников .
- Изотопная двумерная фигура является изотоксальной, т.е. рёберно-транзитивной.
- Изотопная трехмерная фигура является изоэдральной, т.е. гранетранзитивной.
- Изотопная 4-мерная фигура является изохорной, т.е. ячеисто-транзитивной.
Смотрите также
Ссылки
- ^ Маклин, К. Робин (1990), «Подземелья, драконы и кости», The Mathematical Gazette , 74 (469): 243– 256, doi : 10.2307/3619822, JSTOR 3619822, S2CID 195047512.
- ^ Weisstein, Eric W. "Isozonohedron". mathworld.wolfram.com . Получено 26.12.2019 .
- ^ Weisstein, Eric W. "Изоэдр". mathworld.wolfram.com . Получено 21.12.2019 .
- ^ Weisstein, Eric W. "Ромбический икосаэдр". mathworld.wolfram.com . Получено 21.12.2019 .
- ^ Socolar, Joshua ES (2007). "Hexagonal Parquet Tilings: k-Isohedral Monotiles with Arbitraarily Large k" (исправленный PDF) . The Mathematical Intelligencer . 29 (2): 33– 38. arXiv : 0708.2663 . doi :10.1007/bf02986203. S2CID 119365079 . Получено 09.09.2007 .
- ^ Крейг С. Каплан, «Вводная теория мозаики для компьютерной графики». Архивировано 08.12.2022 на Wayback Machine , 2009, Глава 5: «Изоэдральные мозаики», стр. 35.
- ^ Мозаики и узоры , стр. 20, 23.
- ^ «Четырехмерные игральные кости с двадцатью гранями».
Внешние ссылки
- Ольшевский, Джордж. "Изотоп". Глоссарий для гиперпространства . Архивировано из оригинала 4 февраля 2007 года.
- Вайсштейн, Эрик В. "Изоэдральная мозаика". MathWorld .
- Вайсштейн, Эрик В. «Изоэдр». MathWorld .
- изоэдры 25 классов изоэдров с конечным числом сторон
- Дизайн игральных костей в The Dice Lab