Ромбический икосаэдр

Ромбический икосаэдр
Тип	Зоноэдр
Лица	20 равных золотых ромбов
Края	40
Вершины	22
Группа симметрии	Д 5д = Д 5в , [2 + ,10], (2*5)
Характеристики	выпуклый

Ромбический икосаэдр — это многогранник в форме сплющенной сферы . Его 20 граней — это конгруэнтные золотые ромбы; ^[1] 3, 4 или 5 граней сходятся в каждой вершине. Он имеет 5 граней (зеленые на верхнем рисунке), сходящихся в каждом из его 2 полюсов; эти 2 вершины лежат на его оси 5-кратной симметрии, которая перпендикулярна 5 осям 2-кратной симметрии, проходящим через середины противоположных экваториальных ребер (пример на верхнем рисунке: самые левые и самые правые срединные ребра). Его другие 10 граней следуют его экватору, 5 выше и 5 ниже его; каждый из этих 10 ромбов имеет 2 из своих 4 сторон, лежащих на этом зигзагообразном перекошенном десятиугольном экваторе. Ромбический икосаэдр имеет 22 вершины. Он имеет группу симметрии D _{5 d} , [2 ⁺ ,10], (2*5) порядка 20; таким образом, он имеет центр симметрии (так как 5 нечетно).

Несмотря на то, что все его грани конгруэнтны, ромбический икосаэдр не является гранетранзитивным , поскольку можно определить, находится ли конкретная грань вблизи экватора или вблизи полюса, исследуя типы вершин, окружающих эту грань.

Ромбический икосаэдр является зоноэдром .

Ромбический икосаэдр имеет 5 наборов по 8 параллельных ребер, описываемых как 8 ₅ поясов .

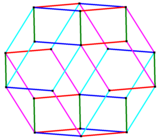Ребра ромбического икосаэдра можно сгруппировать в 5 параллельных наборов, как показано на этой каркасной ортогональной проекции.

Ромбический икосаэдр образует выпуклую оболочку проекции вершины-сначала ^{[ требуется пояснение ]} 5-куба в 3 измерения ^{[ требуется ссылка ]} . 32 вершины 5-куба отображаются в 22 внешние вершины ромбического икосаэдра, а оставшиеся 10 внутренних вершин образуют пятиугольную антипризму .

Таким же образом из 4-куба можно получить ромбододекаэдр , а из 6-куба — ромботриаконтаэдр .

Ромбический икосаэдр можно получить из ромбического триаконтаэдра , удалив пояс из 10 средних граней с параллельными ребрами.

Ромбический триаконтаэдр можно рассматривать как вытянутый ромбический икосаэдр.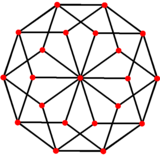

Ромбический икосаэдр и ромбический триаконтаэдр имеют одну и ту же 10-кратно симметричную ортогональную проекцию. (*)

(*) (Например, на левом рисунке):

Ортогональная проекция (вертикального) пояса из 10 средних граней ромбического триаконтаэдра — это просто (горизонтальный) внешний правильный десятиугольник общей ортогональной проекции.

Удаление еще одного пояса из 8 граней с параллельными ребрами из икосаэдра приводит к додекаэдру Билински , который топологически эквивалентен, но не конгруэнтен правильному ромбическому додекаэдру .

• Вайсштейн, Эрик В. "Ромбический икосаэдр". MathWorld .
• http://www.georgehart.com/virtual-polyhedra/zonohedra-info.html
  • Модель VRML [1]