Архитектоническая и катоптрическая мозаика

В геометрии Джон Хортон Конвей определяет архитектонические и катоптрические мозаики как однородные мозаики (или соты ) евклидова 3-пространства с простыми пространственными группами и их двойственными , как трехмерный аналог платоновой, архимедовой и каталонской мозаики плоскости. Особая вершинная фигура архитектонической мозаики является двойственной ячейке соответствующей катоптрической мозаики , и наоборот. Кубиль является единственной платоновой (правильной) мозаикой 3-пространства и является самодвойственной. Существуют другие однородные соты, построенные как гирации или призматические стопки (и их двойственные), которые исключены из этих категорий.

Пары архитектонических и катоптрических мозаик перечислены ниже с их группой симметрии . Эти мозаики представляют только четыре группы пространств симметрии , и все они находятся в кубической кристаллической системе . Многие из этих мозаик могут быть определены в нескольких группах симметрии, поэтому в каждом случае выражается наивысшая симметрия.

Ссылка [1] индексы	Симметрия	Архитектурная мозаика			Катоптрическая мозаика
		Имя Диаграмма Коксетера Изображение	Изображение вершинной фигуры	Клетки	Имя	Клетка	Вершинные фигуры
Дж 11,15 А 1 В 1 Г 22 δ 4	нк [4,3,4]	Cubille (кубические соты)	Октаэдр ,		Кубиль	Куб ,
Дж 12,32 А 15 В 14 Г 7 т 1 δ 4	нк [4,3,4]	Кубооктаэдр (выпрямленные кубические соты)	Кубоид ,		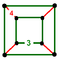сплющенный октаэдр	Равнобедренная квадратная бипирамида	,
J 13 A 14 W 15 G 8 т 0,1 δ 4	нк [4,3,4]	Усеченный кубический сот (усеченные кубические соты)	Равнобедренная квадратная пирамида		Пирамидиллия	Равнобедренная квадратная пирамида	,
J 14 A 17 W 12 G 9 т 0,2 δ 4	нк [4,3,4]	2-RCO-trille (Кантеллированные кубические соты)	Клин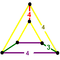		Четверть сплющенный октаэдр	irr. Треугольная бипирамида	,,
J 16 A 3 W 2 G 28 т 1,2 δ 4	до н.э. [[4,3,4]]	Усеченный октаэдр (Усеченные кубические соты)	Тетрагональный двуклиновидный		Сплюснутый тетраэдр	Тетрагональный двуклиновидный
J 17 A 18 W 13 G 25 т 0,1,2 δ 4	нк [4,3,4]	n-tCO-trille (усеченные кубические соты)	Зеркальная клиновидная кость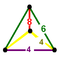		Треугольная пирамидка	Зеркальная клиновидная кость	,,
J 18 A 19 W 19 G 20 т 0,1,3 δ 4	нк [4,3,4]	1-RCO-trille (Runcit-усеченные кубические соты)	Трапециевидная пирамида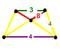		Квадратная четверть пирамидилла	Пирамида ирр.	,,,
J 19 A 22 W 18 G 27 т 0,1,2,3 δ 4	до н.э. [[4,3,4]]	b-tCO-trille (усеченные кубические соты)	Филлик дисфеноидный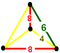		Восьмая пирамидка	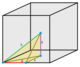Филлик дисфеноидный	,
J 21,31,51 А 2 В 9 Г 1 hδ 4	фк [4,3 1,1 ]	Тетрооктаэдр (Тетраэдрически-октаэдрические соты) или	Кубооктаэдр ,		Додекаэдр или	Ромбический додекаэдр ,	,
J 22,34 А 21 В 17 С 10 ч 2 δ 4	фк [4,3 1,1 ]	усеченный тетраоктаэдр (усеченные тетраэдрально-октаэдрические соты) или	Прямоугольная пирамида		Полусплюснутый октаэдр или	ромбическая пирамида	,,
J 23 A 16 W 11 G 5 h 3 δ 4	фк [4,3 1,1 ]	3-RCO-trille (кантеллированные тетраэдрально-октаэдрические соты) или	Усеченная треугольная пирамида		четверть кубилья	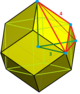ирр. треугольная бипирамида
J 24 A 20 W 16 G 21 h 2,3 δ 4	фк [4,3 1,1 ]	f-tCO-trille (усеченные тетраэдрально-октаэдрические соты) или	Зеркальная клиновидная кость		Половина пирамиды	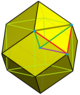Зеркальная клиновидная кость
J 25,33 А 13 В 10 Г 6 qδ 4	г [[3 [4] ]]	Усеченный тетраэдр (циклоусеченные тетраэдрально-октаэдрические соты) или	Равнобедренная треугольная призма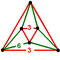		сплющенный кубиль	Треугольный трапецоэдр

Вершинные фигуры всех архитектонических сот и двойные ячейки всех катоптрических сот показаны ниже в том же масштабе и той же ориентации:

Эти четыре группы симметрии обозначены следующим образом:

Этикетка	Описание	космическая группа Международный символ	Геометрическая нотация [2]	нотация Коксетера	Фибрифолдная нотация
до нашей эры	бикубическая симметрия или расширенная кубическая симметрия	(221) Мне 3 м	И43	[[4,3,4]]	8°:2
нк	нормальная кубическая симметрия	(229) Пм 3 м	П43	[4,3,4]	4 − :2
фк	полукубическая симметрия	(225) Фм 3 м	Ф43	[4,3 1,1 ] = [4,3,4,1 + ]	2 − :2
г	симметрия алмаза или расширенная четвертькубическая симметрия	(227) Фд 3 м	Ф д 4 н 3	[[3 [4] ]] = [[1 + ,4,3,4,1 + ]]	2 + :2

• Кристаллография квазикристаллов: концепции, методы и структуры Вальтера Штойрера, Софии Делуди (2009), стр. 54-55. 12 упаковок из 2 или более однородных многогранников с кубической симметрией

• Conway, John H .; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "21. Наименование архимедовых и каталонских многогранников и мозаик". Симметрии вещей . AK Peters, Ltd. стр.  292–298 . ISBN 978-1-56881-220-5.
• Инчбальд, Гай (июль 1997 г.). «Двойственные архимедовы соты». The Mathematical Gazette . 81 (491). Лестер: The Mathematical Association: 213– 219. doi :10.2307/3619198. JSTOR  3619198.[1]
• Бранко Грюнбаум , (1994) Однородные мозаики 3-мерного пространства. Геомбинаторика 4, 49 - 56.
• Норман Джонсон (1991) Однородные многогранники , Рукопись
• А. Андреини , (1905) Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (О правильных и полуправильных сетях многогранников и о соответствующих корреляционных сетях), Mem. Società Italiana della Scienze, Серия 3, 14 75–129. PDF [2]
• Джордж Ольшевский, (2006) Униформные паноплоидные тетракомбы , Рукопись PDF [3]
• Пирс, Питер (1980). Структура в природе — стратегия дизайна. MIT Press. С.  41–47 . ISBN 9780262660457.
• Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [4] 
  • (Документ 24) HSM Coxeter, Регулярные и полурегулярные многогранники III , [Math. Zeit. 200 (1988) 3-45] См. стр. 318 [5]