Дифференциальная геометрия поверхностей

В математике дифференциальная геометрия поверхностей занимается дифференциальной геометрией гладких поверхностей [a] с различными дополнительными структурами, чаще всего римановой метрикой . [b]
Поверхности были тщательно изучены с разных точек зрения: внешне , в отношении их вложения в евклидово пространство и внутренне , отражая их свойства, определяемые исключительно расстоянием внутри поверхности, измеренным вдоль кривых на поверхности. Одной из фундаментальных исследованных концепций является гауссова кривизна , впервые глубоко изученная Карлом Фридрихом Гауссом [ 1], который показал, что кривизна является внутренним свойством поверхности, независимым от ее изометрического вложения в евклидово пространство.
Поверхности естественным образом возникают как графики функций пары переменных и иногда появляются в параметрической форме или как геометрические места , связанные с пространственными кривыми . Важную роль в их изучении сыграли группы Ли (в духе программы Эрлангена ), а именно группы симметрии евклидовой плоскости , сферы и гиперболической плоскости . Эти группы Ли можно использовать для описания поверхностей постоянной гауссовой кривизны; они также обеспечивают существенный ингредиент в современном подходе к внутренней дифференциальной геометрии через связи . С другой стороны, внешние свойства, основанные на вложении поверхности в евклидово пространство, также широко изучались. Это хорошо иллюстрируют нелинейные уравнения Эйлера–Лагранжа в вариационном исчислении : хотя Эйлер разработал уравнения с одной переменной для понимания геодезических , определенных независимо от вложения, одно из основных приложений Лагранжа уравнений с двумя переменными было к минимальным поверхностям , концепции, которая может быть определена только в терминах вложения.
История
,_Mathematician_(2551069295).jpg/440px-Portrait_of_Bernhard_Riemann_(1826-1866),_Mathematician_(2551069295).jpg)
Объемы некоторых квадратных поверхностей вращения были вычислены Архимедом . [2] Развитие исчисления в семнадцатом веке предоставило более систематический способ их вычисления. [3] Кривизна общих поверхностей была впервые изучена Эйлером . В 1760 году [4] он доказал формулу для кривизны плоского сечения поверхности, а в 1771 году [ 5] он рассмотрел поверхности, представленные в параметрической форме. Монж заложил основы их теории в своем классическом мемуаре L'application de l'analyse à la géometrie , который появился в 1795 году. Определяющий вклад в теорию поверхностей был сделан Гауссом в двух замечательных работах, написанных в 1825 и 1827 годах. [1] Это ознаменовало новый отход от традиции, поскольку впервые Гаусс рассмотрел внутреннюю геометрию поверхности, свойства, которые определяются только геодезическими расстояниями между точками на поверхности независимо от конкретного способа, которым поверхность расположена в окружающем евклидовом пространстве. Венчающий результат, Theorema Egregium Гаусса, установил, что гауссова кривизна является внутренним инвариантом, т. е. инвариантом относительно локальных изометрий . Эта точка зрения была распространена на пространства более высоких размерностей Риманом и привела к тому, что сегодня известно как риманова геометрия . Девятнадцатый век был золотым веком теории поверхностей, как с топологической, так и с дифференциально-геометрической точки зрения, и большинство ведущих геометров посвятили себя их изучению. [ необходима ссылка ] Дарбу собрал множество результатов в своем четырехтомном трактате «Теория поверхностей» (1887–1896).
Обзор
Интуитивно вполне привычно говорить, что лист растения, поверхность стакана или форма лица изогнуты определенным образом, и что все эти формы, даже после игнорирования любых отличительных признаков, имеют определенные геометрические особенности, которые отличают их друг от друга. Дифференциальная геометрия поверхностей занимается математическим пониманием таких явлений. Изучение этой области, которая была начата в ее современной форме в 1700-х годах, привело к развитию многомерной и абстрактной геометрии, такой как риманова геометрия и общая теория относительности . [ оригинальное исследование? ]
Основным математическим объектом является регулярная поверхность. Хотя соглашения различаются в их точном определении, они образуют общий класс подмножеств трехмерного евклидова пространства ( ℝ 3 ), которые охватывают часть привычного понятия «поверхность». Анализируя класс кривых, лежащих на такой поверхности, и степень, в которой поверхности заставляют их искривляться в ℝ 3 , можно связать с каждой точкой поверхности два числа, называемые главными кривизнами. Их среднее значение называется средней кривизной поверхности, а их произведение называется гауссовой кривизной.
Существует множество классических примеров регулярных поверхностей, в том числе:
- знакомые примеры, такие как плоскости, цилиндры и сферы
- минимальные поверхности , которые определяются свойством, что их средняя кривизна равна нулю в каждой точке. Наиболее известными примерами являются катеноиды и геликоиды , хотя было обнаружено гораздо больше. Минимальные поверхности также могут быть определены свойствами, связанными с площадью поверхности , в результате чего они предоставляют математическую модель для формы мыльных пленок, натянутых на проволочный каркас
- линейчатые поверхности , то есть поверхности, через каждую точку которых проходит хотя бы одна прямая линия; примерами служат цилиндр и однополостный гиперболоид .
Удивительный результат Карла Фридриха Гаусса , известный как Theorema egregium , показал, что гауссова кривизна поверхности, которая по своему определению связана с тем, как кривые на поверхности меняют направления в трехмерном пространстве, на самом деле может быть измерена длинами кривых, лежащих на поверхностях, вместе с углами, образуемыми при пересечении двух кривых на поверхности. Терминологически это говорит о том, что гауссова кривизна может быть вычислена из первой фундаментальной формы (также называемой метрическим тензором ) поверхности. Вторая фундаментальная форма , напротив, является объектом, который кодирует, как искажаются длины и углы кривых на поверхности, когда кривые отталкиваются от поверхности.
Несмотря на измерение различных аспектов длины и угла, первая и вторая фундаментальные формы не являются независимыми друг от друга, и они удовлетворяют определенным ограничениям, называемым уравнениями Гаусса-Кодацци . Основная теорема, часто называемая фундаментальной теоремой дифференциальной геометрии поверхностей, утверждает, что всякий раз, когда два объекта удовлетворяют ограничениям Гаусса-Кодацци, они возникнут как первая и вторая фундаментальные формы регулярной поверхности.
Используя первую фундаментальную форму, можно определить новые объекты на регулярной поверхности. Геодезические — это кривые на поверхности, которые удовлетворяют определенному обыкновенному дифференциальному уравнению второго порядка , которое задается первой фундаментальной формой. Они очень непосредственно связаны с изучением длин кривых; геодезическая достаточно короткой длины всегда будет кривой наименьшей длины на поверхности, которая соединяет две ее конечные точки. Таким образом, геодезические являются фундаментальными для задачи оптимизации определения кратчайшего пути между двумя заданными точками на регулярной поверхности.
Можно также определить параллельный перенос вдоль любой заданной кривой, который дает предписание о том, как деформировать касательный вектор к поверхности в одной точке кривой в касательные векторы во всех других точках кривой. Предписание определяется обыкновенным дифференциальным уравнением первого порядка , которое задается первой фундаментальной формой.
Вышеуказанные концепции по сути все связаны с многомерным исчислением. Теорема Гаусса-Бонне является более глобальным результатом, который связывает гауссову кривизну поверхности с ее топологическим типом. Она утверждает, что среднее значение гауссовой кривизны полностью определяется эйлеровой характеристикой поверхности вместе с ее площадью поверхности.
Любая регулярная поверхность является примером как риманова многообразия , так и римановой поверхности . По сути, вся теория регулярных поверхностей, обсуждаемая здесь, имеет обобщение в теории римановых многообразий и их подмногообразий.
Регулярные поверхности в евклидовом пространстве
Определение
Интуитивно ясно, что сфера является гладкой, в то время как конус или пирамида, из-за их вершины или ребер, не являются таковыми. Понятие «регулярной поверхности» является формализацией понятия гладкой поверхности. Определение использует локальное представление поверхности через отображения между евклидовыми пространствами . Существует стандартное понятие гладкости для таких отображений; отображение между двумя открытыми подмножествами евклидова пространства является гладким, если его частные производные каждого порядка существуют в каждой точке области. [6] [7] [8]
Ниже приведены три эквивалентных способа представления определения; среднее определение, пожалуй, наиболее наглядно, поскольку оно по сути говорит о том, что регулярная поверхность — это подмножество ℝ 3 , которое локально является графиком гладкой функции (будь то в области в плоскости yz , плоскости xz или плоскости xy ).

| Объекты, используемые в определении | Регулярная поверхность в евклидовом пространстве ℝ 3 — это подмножество S пространства ℝ 3 такое, что каждая точка S имеет... |
|---|---|
| Локальная параметризация | ... открытая окрестность U ⊂ S , для которой существует открытое подмножество V из ℝ 2 и гомеоморфизм f : V → U такой, что
|
| патчи Монжа | ... открытая окрестность U ⊂ ℝ 3 , для которой существует открытое подмножество V из ℝ 2 и гладкая функция h : V → ℝ такая, что выполняется одно из следующих условий:
|
| Неявные функции | ... открытая окрестность U ⊂ ℝ 3 , для которой существует гладкая функция F : U → ℝ с:
|
Гомеоморфизмы, появляющиеся в первом определении, известны как локальные параметризации или локальные системы координат или локальные карты на S. [13] Эквивалентность первых двух определений утверждает, что вокруг любой точки на регулярной поверхности всегда существуют локальные параметризации вида ( u , v ) ↦ ( h ( u , v ), u , v ) , ( u , v ) ↦ ( u , h ( u , v ), v ) , или ( u , v ) ↦ ( u , v , h ( u , v )) , известные как пятна Монжа.. Функции F , как в третьем определении, называются локальными определяющими функциями . Эквивалентность всех трех определений следует из теоремы о неявной функции . [14] [15] [16]

Если заданы любые две локальные параметризации f : V → U и f ′ : V ′→ U ′ регулярной поверхности, композиция f −1 ∘ f ′ обязательно является гладкой как отображение между открытыми подмножествами ℝ 2 . [17] Это показывает, что любая регулярная поверхность естественным образом имеет структуру гладкого многообразия , причем гладкий атлас задается обратными локальными параметризациями.
В классической теории дифференциальной геометрии поверхности обычно изучаются только в регулярном случае. [7] [18] Однако также распространено изучение нерегулярных поверхностей, в которых две частные производные ∂ u f и ∂ v f локальной параметризации могут не быть линейно независимыми . В этом случае S может иметь особенности, такие как ребра возврата . Такие поверхности обычно изучаются в теории особенностей . Другие ослабленные формы регулярных поверхностей встречаются в компьютерном проектировании , где поверхность разбивается на непересекающиеся части, причем производные локальной параметризации даже не могут быть непрерывными вдоль границ. [ требуется ссылка ]
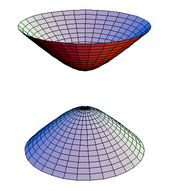
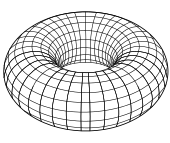

Простые примеры. Простой пример регулярной поверхности даёт 2-сфера {( x , y , z ) | x 2 + y 2 + z 2 = 1 }; эта поверхность может быть покрыта шестью лоскутами Монжа (по два каждого из трёх типов, указанных выше), принимая h ( u , v ) = ± (1 − u 2 − v 2 ) 1/2 . Её также можно покрыть двумя локальными параметризациями, используя стереографическую проекцию . Множество {( x , y , z ) : (( x 2 + y 2 ) 1/2 − r ) 2 + z 2 = R 2 } является тором вращения с радиусами r и R . Это регулярная поверхность; локальные параметризации могут быть заданы в виде
Гиперболоид на двух листах {( x , y , z ) : z 2 = 1 + x 2 + y 2 } является регулярной поверхностью; она может быть покрыта двумя лоскутами Монжа, причем h ( u , v ) = ±(1 + u 2 + v 2 ) 1/2 . Геликоид появляется в теории минимальных поверхностей . Он покрывается единственной локальной параметризацией, f ( u , v ) = ( u sin v , u cos v , v ) .
Касательные векторы и нормальные векторы
Пусть S — регулярная поверхность в ℝ 3 , а p — элемент S . Используя любое из приведенных выше определений, можно выделить некоторые векторы в ℝ 3 как касательные к S в точке p , а некоторые векторы в ℝ 3 как ортогональные к S в точке p .
| Объекты, используемые в определении | Вектор X в ℝ 3 касается S в точке p, если... | Вектор n в ℝ 3 нормален к S в точке p, если... |
|---|---|---|
| Локальная параметризация | ... при любой локальной параметризации f : V → S с p ∈ f ( V ) , X является линейной комбинацией и | ... он ортогонален каждому касательному вектору к S в точке p |
| патчи Монжа | ... для любого патча Монжа ( u , v ) ↦ ( u , v , h ( u , v ) ), диапазон которого включает p , имеем с частными производными, оцененными в точке ( p 1 , p 2 ) . Аналогичное определение применимо в случае пятен Монжа двух других форм. | ... для любого фрагмента Монжа ( u , v ) ↦ ( u , v , h ( u , v )), диапазон которого включает p , n кратно ( ∂ ч/∂ у , ∂ ч/∂ v , −1) как оценено в точке ( p 1 , p 2 ) . Аналогичное определение применимо в случае пятен Монжа двух других форм. |
| Неявные функции | ... для любой локальной определяющей функции F, область определения которой содержит p , X ортогональна ∇ F ( p ) | ... для любой локальной определяющей функции F, область определения которой содержит p , n кратно ∇ F ( p ) |
Видно, что касательное пространство или касательная плоскость к S в точке p , которое определяется как состоящее из всех касательных векторов к S в точке p , является двумерным линейным подпространством ℝ 3 ; его часто обозначают как T p S . Нормальное пространство к S в точке p , которое определяется как состоящее из всех нормальных векторов к S в точке p , является одномерным линейным подпространством ℝ 3 , которое ортогонально касательному пространству T p S . Таким образом, в каждой точке p из S существует два нормальных вектора единичной длины (единичные нормальные векторы). Единичные нормальные векторы в точке p могут быть заданы в терминах локальных параметризаций, патчей Монжа или локальных определяющих функций с помощью формул
следуя тем же обозначениям, что и в предыдущих определениях.
Также полезно отметить «внутреннее» определение касательных векторов, которое типично для обобщения теории регулярных поверхностей на случай гладких многообразий . Оно определяет касательное пространство как абстрактное двумерное действительное векторное пространство, а не как линейное подпространство ℝ 3 . В этом определении говорится, что касательный вектор к S в точке p является присвоением каждой локальной параметризации f : V → S с p ∈ f ( V ) двух чисел X 1 и X 2 , таких что для любой другой локальной параметризации f ′ : V → S с p ∈ f ( V ) (и с соответствующими числами ( X ′) 1 и ( X ′) 2 ) имеем
где A f ′( p ) — матрица Якоби отображения f −1 ∘ f ′ , вычисленная в точке f ′( p ) . Набор касательных векторов к S в точке p естественным образом имеет структуру двумерного векторного пространства. Касательный вектор в этом смысле соответствует касательному вектору в предыдущем смысле, рассматривая вектор
в ℝ 3. Условие Якобиана на X 1 и X 2 гарантирует, по правилу цепочки , что этот вектор не зависит от f .
Для гладких функций на поверхности векторные поля (т. е. касательные векторные поля) имеют важную интерпретацию как операторы первого порядка или деривации. Пусть будет регулярной поверхностью, открытым подмножеством плоскости и координатной картой. Если , пространство можно отождествить с . Аналогично отождествляет векторные поля на с векторными полями на . Принимая стандартные переменные u и v , векторное поле имеет вид , с a и b гладкими функциями. Если является векторным полем и является гладкой функцией, то является также гладкой функцией. Дифференциальный оператор первого порядка является деривацией , т. е. он удовлетворяет правилу Лейбница [19]
Для векторных полей X и Y легко проверить, что оператор является производной, соответствующей векторному полю. Он называется скобкой Ли . Он кососимметричен и удовлетворяет тождеству Якоби:
Подводя итог, можно сказать, что векторные поля на или образуют алгебру Ли под скобкой Ли. [20]
Первая и вторая фундаментальные формы, оператор формы и кривизна
Пусть S — регулярная поверхность в ℝ 3 . При наличии локальной параметризации f : V → S и единичного нормального векторного поля n к f ( V ) можно определить следующие объекты как вещественные или матричнозначные функции на V . Первая фундаментальная форма зависит только от f , а не от n . Четвертый столбец записывает способ, которым эти функции зависят от f , связывая функции E ′, F ′, G ′, L ′ и т. д., возникающие при другом выборе локальной параметризации, f ′ : V ′ → S , с функциями, возникающими для f . Здесь A обозначает матрицу Якоби функции f –1 ∘ f ′ . Ключевое соотношение при установлении формул четвертого столбца тогда
как следует из цепного правила .
| Терминология | Обозначение | Определение | Зависимость от локальной параметризации |
|---|---|---|---|
| Первая фундаментальная форма | Э | ||
| Ф | |||
| Г | |||
| Вторая фундаментальная форма | Л | ||
| М | |||
| Н | |||
| Оператор формы [21] | П | ||
| Гауссова кривизна | К | ||
| Средняя кривизна | ЧАС | ||
| Главные кривизны |
С помощью прямого вычисления с матрицей, определяющей оператор формы, можно проверить, что гауссова кривизна является определителем оператора формы, средняя кривизна равна половине следа оператора формы, а главные кривизны являются собственными значениями оператора формы; более того, гауссова кривизна является произведением главных кривизн, а средняя кривизна является их суммой. Эти наблюдения также можно сформулировать как определения этих объектов. Эти наблюдения также ясно показывают, что последние три строки четвертого столбца немедленно следуют из предыдущей строки, поскольку подобные матрицы имеют идентичные определитель, след и собственные значения. Важно отметить, что E , G и EG − F 2 обязательно положительны. Это гарантирует, что обратная матрица в определении оператора формы хорошо определена, и что главные кривизны являются действительными числами.
Обратите внимание также, что отрицание выбора единичного нормального векторного поля отменит вторую фундаментальную форму, оператор формы, среднюю кривизну и главные кривизны, но оставит гауссову кривизну неизменной. Подводя итог, можно сказать, что при заданной регулярной поверхности S гауссова кривизна S может рассматриваться как вещественнозначная функция на S ; относительно выбора единичного нормального векторного поля на всех S две главные кривизны и средняя кривизна также являются вещественнозначными функциями на S .
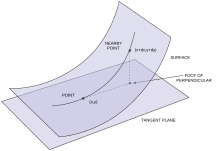

Геометрически первую и вторую фундаментальные формы можно рассматривать как дающие информацию о том, как f ( u , v ) движется в ℝ 3 , как ( u , v ) движется в V . В частности, первая фундаментальная форма кодирует, как быстро движется f , в то время как вторая фундаментальная форма кодирует степень, в которой ее движение происходит в направлении нормального вектора n . Другими словами, вторая фундаментальная форма в точке p кодирует длину ортогональной проекции из S на касательную плоскость к S в p ; в частности, она дает квадратичную функцию, которая наилучшим образом приближает эту длину. Это мышление можно уточнить с помощью формул
как следует непосредственно из определений фундаментальных форм и теоремы Тейлора в двух измерениях. Главные кривизны можно рассматривать следующим образом. В данной точке p плоскости S рассмотрим совокупность всех плоскостей, которые содержат ортогональную прямую к S. Каждая такая плоскость имеет кривую пересечения с S , которую можно рассматривать как плоскую кривую внутри самой плоскости. Две главные кривизны в точке p являются максимальными и минимальными возможными значениями кривизны этой плоской кривой в точке p , поскольку рассматриваемая плоскость вращается вокруг нормальной прямой.
Ниже приводится подведение итогов расчета вышеуказанных величин относительно патча Монжа f ( u , v ) = ( u , v , h ( u , v )) . Здесь h u и h v обозначают две частные производные h , с аналогичными обозначениями для вторых частных производных. Вторая фундаментальная форма и все последующие величины вычисляются относительно заданного выбора единичного нормального векторного поля.
| Количество | Формула |
|---|---|
| Единичное нормальное векторное поле | |
| Первая фундаментальная форма | |
| Вторая фундаментальная форма | |
| Оператор формы | |
| Гауссова кривизна | |
| Средняя кривизна |
Символы Кристоффеля, уравнения Гаусса–Кодацци и теорема Egregium
Пусть S — регулярная поверхность в ℝ 3. Символы Кристоффеля сопоставляют каждой локальной параметризации f : V → S восемь функций на V , определяемых формулой [22]
Их также можно определить следующими формулами, в которых n — единичное нормальное векторное поле вдоль f ( V ) , а L , M , N — соответствующие компоненты второй фундаментальной формы:
Ключ к этому определению заключается в том, что ∂ ф/∂ у , ∂ ф/∂ v и n образуют базис ℝ 3 в каждой точке, относительно которого каждое из трех уравнений однозначно определяет символы Кристоффеля как координаты вторых частных производных f . Выбор единичной нормали не влияет на символы Кристоффеля, поскольку если n заменить на его отрицание, то компоненты второй фундаментальной формы также будут отрицательными, и поэтому знаки Ln , Mn , Nn останутся неизменными.
Второе определение показывает, в контексте локальных параметризаций, что символы Кристоффеля геометрически естественны. Хотя формулы в первом определении кажутся менее естественными, они имеют важное значение, показывая, что символы Кристоффеля могут быть вычислены из первой фундаментальной формы, что не сразу очевидно из второго определения. Эквивалентность определений можно проверить, напрямую подставив первое определение во второе и используя определения E , F , G .
Уравнения Кодацци утверждают, что [23]
Эти уравнения могут быть напрямую выведены из второго определения символов Кристоффеля, данного выше; например, первое уравнение Кодацци получается путем дифференцирования первого уравнения относительно v , второго уравнения относительно u , вычитания двух и взятия скалярного произведения с n . Уравнение Гаусса утверждает, что [24]
Их можно вывести аналогично уравнениям Кодацци, используя уравнения Вайнгартена вместо скалярного произведения с n . Хотя они записаны как три отдельных уравнения, они идентичны, если подставить определения символов Кристоффеля в терминах первой фундаментальной формы. Существует много способов записать полученное выражение, один из них был выведен в 1852 году Бриоши с использованием искусного использования определителей: [25] [26]
Когда символы Кристоффеля рассматриваются как определяемые первой фундаментальной формой, уравнения Гаусса и Кодацци представляют собой определенные ограничения между первой и второй фундаментальными формами. Уравнение Гаусса особенно примечательно, поскольку оно показывает, что гауссова кривизна может быть вычислена непосредственно из первой фундаментальной формы, без необходимости какой-либо другой информации; эквивалентно, это говорит о том, что LN − M 2 на самом деле может быть записана как функция E , F , G , хотя отдельные компоненты L , M , N не могут. Это известно как Theorema egregium и было главным открытием Карла Фридриха Гаусса . Это особенно поразительно, когда вспоминаешь геометрическое определение гауссовой кривизны S как определяемой максимальным и минимальным радиусами соприкасающихся окружностей; они, по-видимому, фундаментально определяются геометрией того, как S изгибается в пределах ℝ 3 . Тем не менее, теорема показывает, что их произведение может быть определено из «внутренней» геометрии S , имея дело только с длинами кривых вдоль S и углами, образованными в их пересечениях. Как сказал Марсель Берже : [27]
Эта теорема сбивает с толку. [...] Это тот тип теоремы, которая могла бы подождать еще десятки лет, прежде чем ее откроет другой математик, поскольку, в отличие от большей части интеллектуальной истории, она совершенно не витала в воздухе. [...] Насколько нам известно, на сегодняшний день не существует простого геометрического доказательства Theorema egregium.
Уравнения Гаусса-Кодацци также могут быть кратко выражены и выведены на языке форм связности благодаря Эли Картану . [28] На языке тензорного исчисления , используя естественные метрики и связности на тензорных расслоениях , уравнение Гаусса можно записать как H 2 − | h | 2 = R , а два уравнения Кодацци можно записать как ∇ 1 h 12 = ∇ 2 h 11 и ∇ 1 h 22 = ∇ 2 h 12 ; сложные выражения, связанные с символами Кристоффеля и первой фундаментальной формой, полностью поглощаются определениями ковариантной тензорной производной ∇ h и скалярной кривизны R . Пьер Бонне доказал, что две квадратичные формы, удовлетворяющие уравнениям Гаусса-Кодацци, всегда однозначно определяют вложенную поверхность локально. [29] По этой причине уравнения Гаусса-Кодацци часто называют фундаментальными уравнениями для вложенных поверхностей, точно определяя, откуда берутся внутренние и внешние кривизны. Они допускают обобщения на поверхности, вложенные в более общие римановы многообразия .
Изометрии
Диффеоморфизм между открытыми множествами и в регулярной поверхности называется изометрией, если он сохраняет метрику, т.е. первую фундаментальную форму. [30] [31] [32] Таким образом, для каждой точки в и касательных векторов в , имеют место равенства
С точки зрения внутреннего произведения, вытекающего из первой фундаментальной формы, это можно переписать как
- .

С другой стороны, длину параметризованной кривой можно рассчитать как
и, если кривая лежит в , правила замены переменных показывают, что
Наоборот, если сохраняет длины всех параметризованных в кривых, то является изометрией. Действительно, для подходящего выбора касательные векторы и дают произвольные касательные векторы и . Равенства должны выполняться для любого выбора касательных векторов и , а также и , так что . [33]
Простой пример изометрии дают две параметризации и открытого множества в регулярные поверхности и . Если , и , то является изометрией на . [34]
Цилиндр и плоскость являются примерами поверхностей, которые локально изометричны, но которые не могут быть расширены до изометрии по топологическим причинам. [35] В качестве другого примера можно привести катеноид и геликоид, которые локально изометричны. [36]
Ковариантные производные
Поле касательных векторов X на S назначает каждому p в S касательный вектор X p к S в точке p . Согласно «внутреннему» определению касательных векторов, данному выше, поле касательных векторов X затем назначает каждой локальной параметризации f : V → S две действительные функции X 1 и X 2 на V , так что
для каждого p в S. Говорят, что X является гладким, если функции X 1 и X 2 являются гладкими для любого выбора f . [37] Согласно другим определениям касательных векторов, данным выше, можно также рассматривать касательное векторное поле X на S как отображение X : S → ℝ 3 такое, что X ( p ) содержится в касательном пространстве T p S ⊂ ℝ 3 для каждого p в S. Как это обычно бывает в более общей ситуации гладких многообразий , касательные векторные поля также можно определить как некоторые дифференциальные операторы в пространстве гладких функций на S.
Ковариантные производные (также называемые «тангенциальными производными») Туллио Леви-Чивиты и Грегорио Риччи-Курбастро предоставляют средство дифференцирования гладких касательных векторных полей. При заданном касательном векторном поле X и касательном векторе Y к S в точке p ковариантная производная ∇ Y X является определенным касательным вектором к S в точке p . Следовательно, если X и Y оба являются касательными векторными полями, то ∇ Y X также можно рассматривать как касательное векторное поле; итеративно, если X , Y , и Z являются касательными векторными полями, можно вычислить ∇ Z ∇ Y X , что будет другим касательным векторным полем. Существует несколько способов определения ковариантной производной; первый из приведенных ниже использует символы Кристоффеля и «внутреннее» определение касательных векторов, а второй является более явно геометрическим.
Если задано касательное векторное поле X и касательный вектор Y к S в точке p , то ∇ Y X определяется как касательный вектор к p , который сопоставляет локальной параметризации f : V → S два числа
где D ( Y 1 , Y 2 ) — производная по направлению . [38] Это часто сокращается до менее громоздкой формы (∇ Y X ) k = ∂ Y ( X k ) + Y i Γ к
ijX j , используя обозначения Эйнштейна и неявно подразумевая места оценки функции. Это следует стандартному предписанию в римановой геометрии для получения связи из римановой метрики . Фундаментальным фактом является то, что вектор
в ℝ 3 не зависит от выбора локальной параметризации f , хотя это довольно утомительно проверять.
Можно также определить ковариантную производную с помощью следующего геометрического подхода, который не использует символы Кристоффеля или локальные параметризации. [39] [40] [41] Пусть X — векторное поле на S , рассматриваемое как функция S → ℝ 3 . Для любой заданной кривой c : ( a , b ) → S можно рассмотреть композицию X ∘ c : ( a , b ) → ℝ 3 . Как отображение между евклидовыми пространствами, его можно дифференцировать при любом входном значении, чтобы получить элемент ( X ∘ c )′( t ) из ℝ 3 . Ортогональная проекция этого вектора на T c ( t ) S определяет ковариантную производную ∇ c ′( t ) X . Хотя это очень геометрически чистое определение, необходимо показать, что результат зависит только от c ′( t ) и X , а не от c и X ; для этого небольшого технического аргумента можно использовать локальные параметризации.
Из второго определения не сразу становится очевидным, что ковариантное дифференцирование зависит только от первой фундаментальной формы S ; однако это немедленно следует из первого определения, поскольку символы Кристоффеля могут быть определены непосредственно из первой фундаментальной формы. Легко проверить, что эти два определения эквивалентны. Ключ в том, что когда мы рассматриваем X 1 ∂ ф/∂ у + X 2 ∂ ф/∂ v как ℝ 3 -значная функция, ее дифференцирование вдоль кривой приводит к вторым частным производным ∂ 2 f ; символы Кристоффеля входят с ортогональной проекцией на касательное пространство из-за формулировки символов Кристоффеля как тангенциальных компонентов вторых производных f относительно базиса ∂ ф/∂ у , ∂ ф/∂ v , н . [38] Это обсуждается в предыдущем разделе.
Правую часть трех уравнений Гаусса можно выразить с помощью ковариантного дифференцирования. Например, правая часть
может быть признана второй координатой
относительно базиса ∂ ф/∂ у , ∂ ф/∂ v , как можно напрямую проверить, используя определение ковариантного дифференцирования с помощью символов Кристоффеля. На языке римановой геометрии это наблюдение можно также сформулировать так, что правые части уравнений Гаусса являются различными компонентами кривизны Риччи связности Леви-Чивиты первой фундаментальной формы, интерпретируемой как риманова метрика .
Примеры

Поверхности вращения
Поверхность вращения получается вращением кривой в плоскости xz вокруг оси z . К таким поверхностям относятся сферы, цилиндры, конусы, торы и катеноид . Общие эллипсоиды , гиперболоиды и параболоиды не являются таковыми. Предположим, что кривая параметризована с помощью
с s , взятым из интервала ( a , b ) . Если c 1 никогда не равен нулю, если c 1 ′ и c 2 ′ никогда не равны нулю одновременно, и если c 1 и c 2 оба гладкие, то соответствующая поверхность вращения
будет регулярной поверхностью в ℝ 3. Локальная параметризация f : ( a , b ) × (0, 2π) → S задается формулой
Относительно этой параметризации геометрические данные следующие: [42]
| Количество | Формула |
|---|---|
| Единичное нормальное векторное поле | |
| Первая фундаментальная форма | |
| Вторая фундаментальная форма | |
| Главные кривизны | |
| Гауссова кривизна | |
| Средняя кривизна |
В частном случае, когда исходная кривая параметризована длиной дуги, т. е. ( c 1 ′( s )) 2 + ( c 2 ′( s )) 2 = 1 , можно дифференцировать, чтобы найти c 1 ′( s ) c 1 ′′( s ) + c 2 ′( s ) c 2 ′′( s ) = 0 . При подстановке в гауссову кривизну получаем упрощенное
Простота этой формулы делает особенно легким изучение класса вращательно-симметричных поверхностей с постоянной гауссовой кривизной. [43] Путем сведения к альтернативному случаю, когда c 2 (s) = s , можно изучать вращательно-симметричные минимальные поверхности, в результате чего любая такая поверхность является частью плоскости или масштабированного катеноида. [44]
Каждая кривая константы t на S может быть параметризована как геодезическая; кривая константы s на S может быть параметризована как геодезическая тогда и только тогда, когда c 1 ′(s) равно нулю. В общем случае геодезические на S управляются соотношением Клеро .

Квадрические поверхности
Рассмотрим квадратичную поверхность, определенную [45]
Эта поверхность допускает параметризацию
Гауссова кривизна и средняя кривизна определяются как

Линейчатые поверхности
Линейчатая поверхность - это поверхность, которая может быть создана движением прямой линии в E 3 . [46] Выбрав направляющую на поверхности, т.е. гладкую кривую единичной скорости c ( t ), ортогональную прямым линиям, а затем выбрав u ( t ) в качестве единичных векторов вдоль кривой в направлении линий, вектор скорости v = c t и u удовлетворяют
Поверхность состоит из точек
при изменении s и t .
Тогда, если
Гауссова и средняя кривизна определяются как
Гауссова кривизна линейчатой поверхности исчезает тогда и только тогда, когда u t и v пропорциональны, [47] Это условие эквивалентно тому, что поверхность является огибающей плоскостей вдоль кривой, содержащей касательный вектор v и ортогональный вектор u , т.е. поверхности, развертывающейся вдоль кривой. [48] В более общем случае поверхность в E 3 имеет исчезающую гауссову кривизну вблизи точки тогда и только тогда, когда она развертывается вблизи этой точки. [49] (Эквивалентное условие дано ниже в терминах метрики.)
Минимальные поверхности
В 1760 году Лагранж распространил результаты Эйлера по вариационному исчислению, включающему интегралы от одной переменной, на две переменные. [50] Он имел в виду следующую задачу:
Для заданной замкнутой кривой в E 3 найдите поверхность, имеющую эту кривую в качестве границы с минимальной площадью.
Такая поверхность называется минимальной поверхностью .
В 1776 году Жан Батист Мёнье показал, что дифференциальное уравнение, выведенное Лагранжем, эквивалентно равенству нулю средней кривизны поверхности:
Поверхность минимальна тогда и только тогда, когда ее средняя кривизна равна нулю.
Минимальные поверхности имеют простую интерпретацию в реальной жизни: это форма, которую примет мыльная пленка, если проволочный каркас в форме кривой окунуть в мыльный раствор, а затем осторожно вынуть. Вопрос о том, существует ли минимальная поверхность с заданной границей, называется проблемой Плато в честь бельгийского физика Жозефа Плато, который проводил эксперименты с мыльными пленками в середине девятнадцатого века. В 1930 году Джесси Дуглас и Тибор Радо дали утвердительный ответ на проблему Плато (Дуглас был награжден одной из первых медалей Филдса за эту работу в 1936 году). [51]
Многие явные примеры минимальной поверхности известны явно, такие как катеноид , геликоид , поверхность Шерка и поверхность Эннепера . В этой области были проведены обширные исследования, обобщенные в Osserman (2002). В частности, результат Osserman показывает, что если минимальная поверхность неплоская, то ее образ при отображении Гаусса плотен в S 2 .
Поверхности постоянной гауссовой кривизны

Если поверхность имеет постоянную гауссову кривизну, она называется поверхностью постоянной кривизны . [52]
- Единичная сфера в E 3 имеет постоянную гауссову кривизну +1.
- Евклидова плоскость и цилиндр имеют постоянную гауссову кривизну 0.
- Единичная псевдосфера имеет постоянную гауссову кривизну -1 (кроме экватора, который является сингулярным ). Псевдосфера может быть получена вращением трактрисы вокруг ее асимптоты. В 1868 году Эудженио Бельтрами показал, что геометрия псевдосферы напрямую связана с геометрией более абстрактной гиперболической плоскости , открытой независимо Лобачевским (1830) и Бойяи (1832). Уже в 1840 году Ф. Миндинг, ученик Гаусса, получил тригонометрические формулы для псевдосферы, идентичные формулам для гиперболической плоскости. [53] Внутренняя геометрия этой поверхности теперь лучше понята в терминах метрики Пуанкаре на верхней полуплоскости или единичном круге и была описана другими моделями, такими как модель Клейна или модель гиперболоида , полученная путем рассмотрения двухполостного гиперболоида q ( x , y , z ) = −1 в трехмерном пространстве Минковского , где q ( x , y , z ) = x 2 + y 2 – z 2 . [54]
Сфера, плоскость и гиперболическая плоскость имеют транзитивную группу Ли симметрии. Этот групповой теоретико-факт имеет далеко идущие последствия, тем более примечательные из-за центральной роли, которую эти специальные поверхности играют в геометрии поверхностей, благодаря теореме Пуанкаре об униформизации (см. ниже).
Другими примерами поверхностей с гауссовой кривизной 0 являются конусы , касательные развертывающиеся поверхности и, в более общем смысле, любые развертывающиеся поверхности.
Локальная метрическая структура
Для любой поверхности, вложенной в евклидово пространство размерности 3 или выше, можно измерить длину кривой на поверхности, угол между двумя кривыми и площадь области на поверхности. Эта структура кодируется бесконечно мало в римановой метрике на поверхности через линейные элементы и элементы площади . Классически в девятнадцатом и начале двадцатого веков рассматривались только поверхности, вложенные в R 3 , и метрика задавалась как положительно определенная матрица 2×2 , плавно изменяющаяся от точки к точке в локальной параметризации поверхности. Идея локальной параметризации и изменения координат была позже формализована через текущее абстрактное понятие многообразия , топологического пространства, где гладкая структура задается локальными картами на многообразии, точно так же, как планета Земля отображается на атласах сегодня. Изменения координат между различными картами одной и той же области должны быть плавными. Так же, как контурные линии на реальных картах кодируют изменения высоты, принимая во внимание локальные искажения поверхности Земли для вычисления истинных расстояний, так и риманова метрика описывает расстояния и площади «в малом» на каждой локальной карте. На каждой локальной карте риманова метрика задается путем плавного назначения положительно определенной матрицы 2×2 каждой точке; когда берется другая карта, матрица преобразуется в соответствии с матрицей Якоби изменения координат. Тогда многообразие имеет структуру двумерного риманова многообразия .
Оператор формы

Дифференциал dn отображения Гаусса n может быть использован для определения типа внешней кривизны, известного как оператор формы [55] или отображение Вайнгартена . Этот оператор впервые появился неявно в работе Вильгельма Блашке , а затем явно в трактате Бурали-Форти и Бургати. [56] Поскольку в каждой точке x поверхности касательное пространство является пространством внутреннего произведения , оператор формы S x может быть определен как линейный оператор в этом пространстве по формуле
для касательных векторов v , w (скалярное произведение имеет смысл, поскольку dn ( v ) и w оба лежат в E 3 ). [c] Правая часть симметрична относительно v и w , поэтому оператор формы является самосопряженным в касательном пространстве. Собственные значения S x — это просто главные кривизны k 1 и k 2 в точке x . В частности, определитель оператора формы в точке — это гауссова кривизна, но он также содержит другую информацию, поскольку средняя кривизна составляет половину следа оператора формы. Средняя кривизна — это внешний инвариант. Во внутренней геометрии цилиндр является развертываемым, что означает, что каждая его часть внутренне неотличима от части плоскости, поскольку его гауссова кривизна тождественно равна нулю. Однако его средняя кривизна не равна нулю; следовательно, внешне он отличен от плоскости.
Эквивалентно оператор формы может быть определен как линейный оператор на касательных пространствах, S p : T p M → T p M. Если n — единичное нормальное поле к M , а v — касательный вектор, то
(нет единого мнения о том, следует ли использовать в определении знак + или −).
В общем случае собственные векторы и собственные значения оператора формы в каждой точке определяют направления, в которых поверхность изгибается в каждой точке. Собственные значения соответствуют главным кривизнам поверхности, а собственные векторы — соответствующим главным направлениям. Главные направления определяют направления, в которых должна перемещаться кривая, встроенная в поверхность, чтобы иметь максимальную и минимальную кривизну, которые задаются главными кривизнами.
Геодезические кривые на поверхности
Кривые на поверхности, которые минимизируют длину между конечными точками, называются геодезическими ; они представляют собой форму, которую приняла бы эластичная лента, натянутая между двумя точками. Математически они описываются с помощью обыкновенных дифференциальных уравнений и вариационного исчисления . Дифференциальная геометрия поверхностей вращается вокруг изучения геодезических. До сих пор остается открытым вопрос, возникает ли каждая риманова метрика на двумерной локальной карте из вложения в трехмерное евклидово пространство: теория геодезических использовалась, чтобы показать, что это верно в важном случае, когда компоненты метрики являются аналитическими .
Геодезические
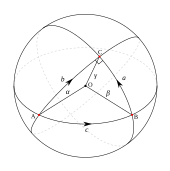
Если задан кусочно-гладкий путь c ( t ) = ( x ( t ), y ( t )) на графике для t в [ a , b ] , его длина определяется как
и энергия
Длина не зависит от параметризации пути. Согласно уравнениям Эйлера–Лагранжа , если c ( t ) — путь, минимизирующий длину, параметризованный длиной дуги , он должен удовлетворять уравнениям Эйлера
где символы Кристоффеля Γк
ijдаются
где g 11 = E , g 12 = F , g 22 = G и g ij — обратная матрица к g ij . Путь, удовлетворяющий уравнениям Эйлера, называется геодезической . По неравенству Коши–Шварца путь, минимизирующий энергию, — это просто геодезическая, параметризованная длиной дуги; и для любой геодезической параметр t пропорционален длине дуги. [57]
Геодезическая кривизна
Геодезическая кривизна k g в точке кривой c ( t ) , параметризованной длиной дуги, на ориентированной поверхности определяется как [58]
где n ( t ) — «главная» единица нормали к кривой поверхности, построенная путем поворота единичного касательного вектора ċ ( t ) на угол +90°.
- Геодезическая кривизна в точке является внутренним инвариантом, зависящим только от метрики вблизи точки.
- Кривая единичной скорости на поверхности является геодезической тогда и только тогда, когда ее геодезическая кривизна равна нулю во всех точках кривой.
- Кривая единичной скорости c ( t ) на вложенной поверхности является геодезической тогда и только тогда, когда ее вектор ускорения c̈ ( t ) перпендикулярен поверхности.
Геодезическая кривизна точно измеряет, насколько далека кривая на поверхности от геодезической.
Ортогональные координаты
Когда F = 0 по всей координатной карте, например, с геодезическими полярными координатами, обсуждаемыми ниже, изображения линий, параллельных осям x и y, являются ортогональными и обеспечивают ортогональные координаты . Если H = ( EG ) 1 ⁄ 2 , то гауссова кривизна определяется как [59]
Если вдобавок E = 1 , так что H = G 1 ⁄ 2 , то угол φ на пересечении геодезической ( x ( t ), y ( t )) и линии y = const задается уравнением
Производная φ определяется классической производной формулой Гаусса: [60]
Геодезические полярные координаты


Как только на поверхности задана метрика и зафиксирована базовая точка, существует уникальная геодезическая, соединяющая базовую точку с каждой достаточно близкой точкой. Направление геодезической в базовой точке и расстояние однозначно определяют другую конечную точку. Эти два бита данных, направление и величина, таким образом, определяют касательный вектор в базовой точке. Отображение от касательных векторов к конечным точкам плавно выметает окрестность базовой точки и определяет то, что называется экспоненциальной картой , определяющей локальную координатную карту в этой базовой точке. Выметенная окрестность имеет свойства, похожие на свойства шаров в евклидовом пространстве, а именно, любые две точки в ней соединены уникальной геодезической. Это свойство называется «геодезической выпуклостью», а координаты называются нормальными координатами . Явное вычисление нормальных координат может быть выполнено путем рассмотрения дифференциального уравнения, которому удовлетворяют геодезические. Свойства выпуклости являются следствиями леммы Гаусса и ее обобщений. Грубо говоря, эта лемма утверждает, что геодезические, начинающиеся в базовой точке, должны пересекать сферы фиксированного радиуса с центром в базовой точке под прямым углом. Геодезические полярные координаты получаются путем объединения экспоненциального отображения с полярными координатами на касательных векторах в базовой точке. Гауссова кривизна поверхности затем задается отклонением второго порядка метрики в этой точке от евклидовой метрики. В частности, гауссова кривизна является инвариантом метрики, знаменитой теоремы Гаусса Egregium . Удобный способ понять кривизну исходит из обыкновенного дифференциального уравнения, впервые рассмотренного Гауссом и позднее обобщенного Якоби, возникающего из изменения нормальных координат относительно двух различных точек. Уравнение Гаусса–Якоби предоставляет другой способ вычисления гауссовой кривизны. Геометрически это объясняет, что происходит с геодезическими из фиксированной базовой точки, когда конечная точка изменяется вдоль малого сегмента кривой посредством данных, записанных в поле Якоби , векторном поле вдоль геодезической. [61] Спустя один с четвертью век после Гаусса и Якоби Марстон Морзе дал более концептуальную интерпретацию поля Якоби в терминах вторых производных функции энергии на бесконечномерном гильбертовом многообразии путей. [62]
Экспоненциальная карта
Теория обыкновенных дифференциальных уравнений показывает, что если f ( t , v ) гладкая, то дифференциальное уравнение дв/дт = f ( t , v ) с начальным условием v (0) = v 0 имеет единственное решение для | t | достаточно малого и решение гладко зависит от t и v 0 . Это означает, что для достаточно малых касательных векторов v в заданной точке p = ( x 0 , y 0 ) существует геодезическая c v ( t ), определенная на (−2, 2) с c v (0) = ( x 0 , y 0 ) и ċ v (0) = v . Более того, если | s | ≤ 1 , то c sv = c v ( st ) . Экспоненциальное отображение определяется как
- ехр р ( v ) = c v (1)
и дает диффеоморфизм между диском ‖ v ‖ < δ и окрестностью p ; в более общем случае отображение, отправляющее ( p , v ) в exp p ( v ), дает локальный диффеоморфизм на окрестность ( p , p ) . Экспоненциальное отображение дает геодезические нормальные координаты вблизи p . [63]
Вычисление нормальных координат
Существует стандартная техника (см., например, Berger (2004)) для вычисления замены переменных на нормальные координаты u , v в точке как формальное разложение в ряд Тейлора . Если координаты x , y в точке (0,0) локально ортогональны, запишите
- x ( u , v ) = αu + L ( u , v ) + λ ( u , v ) + …
- y ( ты , v ) знак равно βv + M ( ты , v ) + µ ( ты , v ) + …
где L , M — квадратичные, а λ , μ — кубические однородные многочлены относительно u и v . Если u и v фиксированы, x ( t ) = x ( tu , tv ) и y ( t ) = y ( tu , tv ) можно рассматривать как формальные решения степенных рядов уравнений Эйлера: это однозначно определяет α , β , L , M , λ и μ .
Лемма Гаусса

В этих координатах матрица g ( x ) удовлетворяет условию g (0) = I , а прямые t ↦ tv являются геодезическими, проходящими через 0. Уравнения Эйлера подразумевают матричное уравнение
- г ( v ) v = v ,
ключевой результат, обычно называемый леммой Гаусса . Геометрически он утверждает, что
геодезические линии, проходящие через точку 0, пересекают окружности с центром в точке 0 ортогонально .
Принимая полярные координаты ( r , θ ) , следует, что метрика имеет вид
- ds 2 знак равно dr 2 + г ( р , θ ) dθ 2 .
В геодезических координатах легко проверить, что геодезические, проходящие через ноль, минимизируют длину. Топология на римановом многообразии тогда задается функцией расстояния d ( p , q ) , а именно инфимумом длин кусочно-гладких путей между p и q . Это расстояние реализуется локально геодезическими, так что в нормальных координатах d (0, v ) = ‖ v ‖ . Если радиус δ взять достаточно малым, небольшое усиление леммы Гаусса показывает, что образ U диска ‖ v ‖ < δ при экспоненциальном отображении является геодезически выпуклым , т. е. любые две точки в U соединены единственной геодезической, лежащей полностью внутри U . [64] [65]
Теорема Эгрегиум

Теорема Гаусса Egregium , «Замечательная теорема», показывает, что гауссова кривизна поверхности может быть вычислена исключительно в терминах метрики и, таким образом, является внутренним инвариантом поверхности, независимым от любого изометрического вложения в E 3 и неизменным при преобразованиях координат. В частности, изометрии и локальные изометрии поверхностей сохраняют гауссову кривизну. [66]
Эту теорему можно выразить в терминах разложения метрики ds в степенной ряд , заданной в нормальных координатах ( u , v ) как
- ds 2 знак равно du 2 + dv 2 - K ( ты dv – v du ) 2 /12 + … .
Уравнение Гаусса–Якоби
Принимая изменение координат от нормальных координат в точке p к нормальным координатам в близлежащей точке q , получаем уравнение Штурма–Лиувилля, которому удовлетворяет уравнение H ( r , θ ) = G ( r , θ ) 1 ⁄ 2 , открытое Гауссом и позднее обобщенное Якоби ,
- H рр = – KH .
Якобиан этого изменения координат в точке q равен H r . Это дает другой способ установления внутренней природы гауссовой кривизны. Поскольку H ( r , θ ) можно интерпретировать как длину линейного элемента в направлении θ , уравнение Гаусса–Якоби показывает, что гауссова кривизна измеряет распространение геодезических на геометрической поверхности по мере их удаления от точки. [67]
Оператор Лапласа-Бельтрами
На поверхности с локальной метрикой
где H 2 = EG − F 2 , гауссова кривизна в точке определяется формулой [68]
где r обозначает геодезическое расстояние от точки.
В изотермических координатах , впервые рассмотренных Гауссом, метрика должна иметь специальный вид
В этом случае оператор Лапласа–Бельтрами имеет вид
и φ удовлетворяет уравнению Лиувилля [69]
Известно, что изотермические координаты существуют в окрестности любой точки на поверхности, хотя все доказательства на сегодняшний день опираются на нетривиальные результаты по уравнениям в частных производных . [70] Существует элементарное доказательство для минимальных поверхностей. [71]
Теорема Гаусса–Бонне

На сфере или гиперболоиде площадь геодезического треугольника , то есть треугольника, все стороны которого являются геодезическими, пропорциональна разности суммы внутренних углов и π . Константа пропорциональности — это просто гауссова кривизна, константа для этих поверхностей. Для тора разность равна нулю, что отражает тот факт, что его гауссова кривизна равна нулю. Это стандартные результаты в сферической, гиперболической и школьной тригонометрии (см. ниже). Гаусс обобщил эти результаты на произвольную поверхность, показав, что интеграл гауссовой кривизны по внутренней части геодезического треугольника также равен этой разности углов или избытку. Его формула показала, что гауссова кривизна может быть вычислена вблизи точки как предел площади по избытку углов для геодезических треугольников, сжимающихся к точке. Поскольку любая замкнутая поверхность может быть разложена на геодезические треугольники, формулу также можно использовать для вычисления интеграла кривизны по всей поверхности. Как частный случай того, что сейчас называется теоремой Гаусса–Бонне , Гаусс доказал, что этот интеграл был замечательно всегда 2π, умноженным на целое число, топологический инвариант поверхности, называемый характеристикой Эйлера . Этот инвариант легко вычислить комбинаторно в терминах числа вершин, ребер и граней треугольников в разложении, также называемом триангуляцией . Это взаимодействие между анализом и топологией было предшественником многих более поздних результатов в геометрии, достигших кульминации в теореме Атьи–Зингера об индексе . В частности, свойства кривизны накладывают ограничения на топологию поверхности.
Геодезические треугольники
Гаусс доказал, что если Δ — геодезический треугольник на поверхности с углами α , β и γ в вершинах A , B и C , то
Фактически, беря геодезические полярные координаты с началом A и AB , AC радиусы под полярными углами 0 и α :
где второе равенство следует из уравнения Гаусса–Якоби, а четвертое — из производной формулы Гаусса в ортогональных координатах ( r , θ ) .
Формула Гаусса показывает, что кривизна в точке может быть вычислена как предел превышения угла α + β + γ − π по площади для последовательно меньших геодезических треугольников вблизи точки. Качественно поверхность положительно или отрицательно искривлена в соответствии со знаком превышения угла для произвольно малых геодезических треугольников. [49]
Теорема Гаусса–Бонне

Поскольку каждое компактное ориентированное 2-многообразие M можно триангулировать малыми геодезическими треугольниками, то отсюда следует, что
где χ ( M ) обозначает эйлерову характеристику поверхности.
Фактически, если имеется F граней, E ребер и V вершин, то 3 F = 2 E и левая часть равна 2π V – π F = 2π( V – E + F ) = 2π χ ( M ) .
Это знаменитая теорема Гаусса–Бонне : она показывает, что интеграл гауссовой кривизны является топологическим инвариантом многообразия, а именно характеристикой Эйлера. Эту теорему можно интерпретировать многими способами; возможно, одной из самых далеко идущих была теорема об индексе для эллиптического дифференциального оператора на M , один из простейших случаев теоремы Атьи–Зингера об индексе . Другой связанный результат, который можно доказать с помощью теоремы Гаусса–Бонне, — это теорема Пуанкаре–Хопфа об индексе для векторных полей на M , которые обращаются в нуль только в конечном числе точек: сумма индексов в этих точках равна характеристике Эйлера, где индекс точки определяется следующим образом: на малой окружности вокруг каждого изолированного нуля векторное поле определяет отображение в единичную окружность; индекс — это просто число оборотов этого отображения.) [49] [72] [73]
Кривизна и вложения
Если гауссова кривизна поверхности M всюду положительна, то эйлерова характеристика положительна, поэтому M гомеоморфна (и, следовательно, диффеоморфна) S 2 . Если, кроме того, поверхность изометрически вложена в E 3 , отображение Гаусса обеспечивает явный диффеоморфизм. Как заметил Адамар , в этом случае поверхность выпукла ; этот критерий выпуклости можно рассматривать как двумерное обобщение хорошо известного критерия второй производной для выпуклости плоских кривых. Гильберт доказал, что каждая изометрически вложенная замкнутая поверхность должна иметь точку положительной кривизны. Таким образом, замкнутое риманово 2-многообразие неположительной кривизны никогда не может быть изометрически вложено в E 3 ; однако, как показал Адриано Гарсия , используя уравнение Бельтрами для квазиконформных отображений , это всегда возможно для некоторой конформно эквивалентной метрики. [74]
Поверхности постоянной кривизны
Односвязные поверхности постоянной кривизны 0, +1 и –1 — это евклидова плоскость, единичная сфера в E 3 и гиперболическая плоскость . Каждая из них имеет транзитивную трехмерную группу Ли сохраняющих ориентацию изометрий G , которую можно использовать для изучения их геометрии. Каждая из двух некомпактных поверхностей может быть отождествлена с фактором G / K , где K — максимальная компактная подгруппа G . Здесь K изоморфна SO(2) . Любое другое замкнутое риманово 2-многообразие M постоянной гауссовой кривизны после масштабирования метрики на постоянный множитель , если необходимо, будет иметь одну из этих трех поверхностей в качестве своего универсального накрывающего пространства . В ориентируемом случае фундаментальную группу Γ группы M можно отождествить с равномерной подгруппой без кручения группы G , а затем M можно отождествить с двойным пространством смежных классов Γ \ G / K . В случае сферы и евклидовой плоскости единственными возможными примерами являются сама сфера и торы, полученные как факторы R2 по дискретным подгруппам ранга 2. Для замкнутых поверхностей рода g ≥ 2 пространство модулей римановых поверхностей, полученных как Γ , варьируется по всем таким подгруппам, имеет действительную размерность 6g − 6. [ 75] По теореме Пуанкаре об униформизации любое ориентируемое замкнутое 2-многообразие конформно эквивалентно поверхности постоянной кривизны 0, +1 или –1. Другими словами, умножая метрику на положительный масштабный коэффициент, можно заставить гауссову кривизну принимать ровно одно из этих значений (знак эйлеровой характеристики M ). [76]
Евклидова геометрия

В случае евклидовой плоскости группа симметрии — это евклидова группа движений , полупрямое произведение двумерной группы переносов на группу вращений. [77] Геодезические линии — это прямые линии, а геометрия закодирована в элементарных формулах тригонометрии , таких как правило, теорема косинусов для треугольника со сторонами a , b , c и углами α , β , γ :
Плоские торы могут быть получены путем факторизации R 2 по решетке , т. е. свободной абелевой подгруппе ранга 2. Эти замкнутые поверхности не имеют изометрических вложений в E 3 . Тем не менее, они допускают изометрические вложения в E 4 ; в простейшем случае это следует из того факта, что тор является произведением двух окружностей, и каждая окружность может быть изометрически вложена в E 2 . [78]
Сферическая геометрия

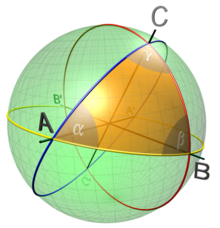
Группа изометрий единичной сферы S 2 в E 3 является ортогональной группой O(3) с группой вращений SO(3) в качестве подгруппы изометрий, сохраняющих ориентацию. Это прямое произведение SO(3) с антиподальным отображением , переводящим x в – x . [79] Группа SO(3) действует транзитивно на S 2 . Подгруппа стабилизатора единичного вектора (0,0,1) может быть отождествлена с SO(2) , так что S 2 = SO(3)/SO(2) .
Геодезические линии между двумя точками на сфере — это дуги большого круга с этими заданными конечными точками. Если точки не являются антиподами, то между ними существует единственная кратчайшая геодезическая линия. Геодезические линии также можно описать теоретически группой: каждая геодезическая линия, проходящая через Северный полюс (0,0,1), является орбитой подгруппы вращений вокруг оси через антиподы на экваторе.
Сферический треугольник — это геодезический треугольник на сфере. Он определяется точками A , B , C на сфере со сторонами BC , CA , AB, образованными дугами большого круга длиной меньше π . Если длины сторон равны a , b , c , а углы между сторонами α , β , γ , то сферический закон косинусов гласит, что
Площадь треугольника определяется по формуле
- Площадь = α + β + γ − π .
Используя стереографическую проекцию из Северного полюса, сферу можно отождествить с расширенной комплексной плоскостью C ∪ {∞} . Явное отображение задается как
При таком соответствии каждый поворот S 2 соответствует преобразованию Мёбиуса в SU(2) , уникальному с точностью до знака. [80] Относительно координат ( u , v ) в комплексной плоскости сферическая метрика становится [81]
Единичная сфера — это единственная замкнутая ориентируемая поверхность с постоянной кривизной +1. Фактор SO(3)/O(2) можно отождествить с вещественной проективной плоскостью . Он неориентируем и может быть описан как фактор S 2 по антиподальному отображению (умножение на −1). Сфера односвязна, в то время как вещественная проективная плоскость имеет фундаментальную группу Z 2 . Конечные подгруппы SO(3) , соответствующие конечным подгруппам O(2) и группам симметрии платоновых тел , не действуют свободно на S 2 , поэтому соответствующие факторы не являются 2-многообразиями, а просто орбифолдами .
Гиперболическая геометрия

Неевклидова геометрия [82] впервые обсуждалась в письмах Гаусса, который провел обширные вычисления на рубеже девятнадцатого века, которые, хотя и распространялись в частном порядке, он решил не публиковать. В 1830 году Лобачевский и независимо в 1832 году Бойяи , сын одного из корреспондентов Гаусса, опубликовали синтетические версии этой новой геометрии, за что подверглись жесткой критике. Однако только в 1868 году Бельтрами, а затем Клейн в 1871 году и Пуанкаре в 1882 году дали конкретные аналитические модели для того, что Клейн назвал гиперболической геометрией . Четыре модели двумерной гиперболической геометрии, которые появились, были:
- модель Бельтрами -Клейна ;
- диск Пуанкаре ;
- верхняя полуплоскость Пуанкаре ;
- гиперболоидная модель Вильгельма Киллинга в трехмерном пространстве Минковского .
Первая модель, основанная на диске, имеет то преимущество, что геодезические на самом деле являются отрезками прямых (то есть пересечениями евклидовых линий с открытым единичным диском). Последняя модель имеет то преимущество, что она дает конструкцию, которая полностью параллельна конструкции единичной сферы в трехмерном евклидовом пространстве. Однако из-за их применения в комплексном анализе и геометрии модели Пуанкаре являются наиболее широко используемыми: они взаимозаменяемы благодаря преобразованиям Мёбиуса между диском и верхней полуплоскостью.
Позволять
быть диском Пуанкаре в комплексной плоскости с метрикой Пуанкаре
В полярных координатах ( r , θ ) метрика задается выражением
Длина кривой γ :[ a , b ] → D определяется формулой
Группа G = SU(1,1) задается формулой
действует транзитивно посредством преобразований Мёбиуса на D , а стабилизирующая подгруппа 0 является группой вращений
Фактор-группа SU(1,1)/± I — это группа изометрий D , сохраняющих ориентацию . Любые две точки z , w в D соединены единственной геодезической, заданной частью окружности или прямой, проходящей через z и w и ортогональной граничной окружности. Расстояние между z и w задается как
В частности, d (0, r ) = 2 tanh −1 r и c ( t ) = 1/2 tanh t — геодезическая линия, проходящая через 0 вдоль действительной оси, параметризованная длиной дуги.
Топология, определяемая этой метрикой, эквивалентна обычной евклидовой топологии, хотя как метрическое пространство ( D , d ) является полной.
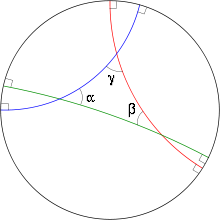
Гиперболический треугольник является геодезическим треугольником для этой метрики: любые три точки в D являются вершинами гиперболического треугольника. Если стороны имеют длину a , b , c с соответствующими углами α , β , γ , то правило гиперболического косинуса гласит, что
Площадь гиперболического треугольника определяется по формуле [83]
- Площадь = π – α – β – γ .
Единичный круг и верхняя полуплоскость
конформно эквивалентны преобразованиям Мёбиуса
При этом соответствии действие SL(2,R) посредством преобразований Мёбиуса на H соответствует действию SU(1,1) на D. Метрика на H становится
Поскольку линии или окружности сохраняются при преобразованиях Мёбиуса, геодезические снова описываются линиями или окружностями, ортогональными действительной оси.
Единичный круг с метрикой Пуанкаре — это единственное односвязное ориентированное двумерное риманово многообразие с постоянной кривизной −1. Любая ориентированная замкнутая поверхность M с этим свойством имеет D в качестве своего универсального накрывающего пространства. Ее фундаментальную группу можно отождествить с конкомпактной подгруппой Γ без кручения группы SU(1,1) таким образом, что
В этом случае Γ — конечно представленная группа . Генераторы и соотношения закодированы в геодезически выпуклом фундаментальном геодезическом многоугольнике в D (или H ), геометрически соответствующем замкнутым геодезическим на M.
Примеры .
- поверхность Больца рода 2;
- квартика Клейна рода 3;
- поверхность Макбита рода 7;
- Первый триплет Гурвица рода 14.
Униформизация
Если задана ориентированная замкнутая поверхность M с гауссовой кривизной K , метрику на M можно изменить конформно, масштабировав ее на коэффициент e 2 u . Новая гауссова кривизна K′ тогда задается как
где Δ — лапласиан для исходной метрики. Таким образом, чтобы показать, что данная поверхность конформно эквивалентна метрике с постоянной кривизной K′, достаточно решить следующий вариант уравнения Лиувилля :
Когда M имеет эйлерову характеристику 0, то он диффеоморфен тору , K ′ = 0 , так что это равносильно решению
Согласно стандартной эллиптической теории, это возможно, поскольку интеграл K по M равен нулю по теореме Гаусса–Бонне. [84]
Если M имеет отрицательную эйлерову характеристику, K′ = −1 , то уравнение, которое нужно решить, имеет вид:
Используя непрерывность экспоненциального отображения в пространстве Соболева, предложенную Нилом Трудингером , это нелинейное уравнение всегда можно решить. [85]
Наконец, в случае 2-сферы K′ = 1 и уравнение принимает вид:
До сих пор это нелинейное уравнение не было проанализировано напрямую, хотя классические результаты, такие как теорема Римана–Роха, подразумевают, что оно всегда имеет решение. [86] Метод потока Риччи , разработанный Ричардом С. Гамильтоном , дает еще одно доказательство существования, основанное на нелинейных уравнениях в частных производных для доказательства существования. [87] Фактически поток Риччи на конформных метриках на S 2 определяется на функциях u ( x , t ) как
По истечении конечного времени Чжоу показал, что K′ становится положительным; предыдущие результаты Гамильтона затем можно было использовать для того, чтобы показать, что K′ сходится к +1. [88] До этих результатов о потоке Риччи Осгуд, Филлипс и Сарнак (1988) предложили альтернативный и технически более простой подход к униформизации, основанный на потоке в римановых метриках g, определяемом как log det Δ g .
Доказательство с использованием эллиптических операторов, обнаруженное в 1988 году, можно найти в Ding (2001). Пусть G — функция Грина на S 2 , удовлетворяющая Δ G = 1 + 4π δ P , где δ P — точечная мера в фиксированной точке P из S 2 . Уравнение Δ v = 2 K – 2 имеет гладкое решение v , поскольку правая часть имеет интеграл 0 по теореме Гаусса–Бонне. Таким образом, φ = 2 G + v удовлетворяет Δ φ = 2 K вдали от P . Отсюда следует, что g 1 = e φ g — полная метрика постоянной кривизны 0 на дополнении P , которая, следовательно, изометрична плоскости. Составляя со стереографической проекцией , следует, что существует гладкая функция u такая, что e 2 ug имеет гауссову кривизну +1 на дополнении P . Функция u автоматически расширяется до гладкой функции на всем S 2 . [d]
Риманова связность и параллельный перенос

Классический подход Гаусса к дифференциальной геометрии поверхностей был стандартным элементарным подходом [89] , который предшествовал появлению концепций риманова многообразия, инициированных Бернхардом Риманом в середине девятнадцатого века, и связности, разработанной Туллио Леви-Чивитой , Эли Картаном и Германом Вейлем в начале двадцатого века. Понятие связности, ковариантной производной и параллельного переноса дало более концептуальный и единообразный способ понимания кривизны, который не только позволял делать обобщения на многообразия более высоких размерностей, но и предоставлял важный инструмент для определения новых геометрических инвариантов, называемых характеристическими классами . [90] Подход, использующий ковариантные производные и связности, в настоящее время принят в более продвинутых учебниках. [91]
Ковариантная производная
Связи на поверхности можно определить с различных эквивалентных, но одинаково важных точек зрения. Риманова связность или связность Леви-Чивиты [92] , возможно, проще всего понять в терминах подъема векторных полей , рассматриваемых как дифференциальные операторы первого порядка, действующие на функции на многообразии, к дифференциальным операторам на касательном расслоении или расслоении фреймов . В случае вложенной поверхности подъем до оператора на векторных полях, называемый ковариантной производной , очень просто описывается в терминах ортогональной проекции. Действительно, векторное поле на поверхности, вложенной в R 3 , можно рассматривать как функцию от поверхности в R 3 . Другое векторное поле действует как дифференциальный оператор покомпонентно. Результирующее векторное поле не будет касательным к поверхности, но это можно исправить, взяв его ортогональную проекцию на касательное пространство в каждой точке поверхности. Как поняли Риччи и Леви-Чивита на рубеже двадцатого века, этот процесс зависит только от метрики и может быть локально выражен в терминах символов Кристоффеля.

Параллельный транспорт
Параллельный перенос касательных векторов вдоль кривой на поверхности был следующим крупным достижением в этой области, благодаря Леви-Чивите . [49] Он связан с более ранним понятием ковариантной производной, поскольку является монодромией обыкновенного дифференциального уравнения на кривой, определяемой ковариантной производной относительно вектора скорости кривой. Параллельный перенос вдоль геодезических, «прямых линий» поверхности, также может быть легко описан напрямую. Вектор в касательной плоскости переносится вдоль геодезической как уникальное векторное поле с постоянной длиной и образует постоянный угол с вектором скорости геодезической. Для общей кривой этот процесс должен быть изменен с использованием геодезической кривизны, которая измеряет, насколько кривая отклоняется от того, чтобы быть геодезической. [64]
Вектор v ( t ) вдоль кривой единичной скорости c ( t ) с геодезической кривизной k g ( t ) называется параллельным вдоль кривой, если
- имеет постоянную длину
- угол θ ( t ) , который он образует с вектором скорости ċ ( t ), удовлетворяет условию
Это восстанавливает правило параллельного переноса вдоль геодезической или кусочно-геодезической кривой, поскольку в этом случае k g = 0 , так что угол θ ( t ) должен оставаться постоянным на любом геодезическом сегменте. Существование параллельного переноса следует из того, что θ ( t ) можно вычислить как интеграл геодезической кривизны. Поскольку он, следовательно, непрерывно зависит от нормы L 2 k g , отсюда следует, что параллельный перенос для произвольной кривой можно получить как предел параллельного переноса при аппроксимации кусочно-геодезических кривых. [93]
Таким образом, связь может быть описана в терминах подъема путей в многообразии к путям в касательном или ортонормальном расслоении фрейма, тем самым формализуя классическую теорию « движущейся системы отсчета », предпочитаемую французскими авторами. [94] Подъемы петель вокруг точки приводят к появлению группы голономии в этой точке. Гауссова кривизна в точке может быть восстановлена из параллельного переноса вокруг все более малых петель в точке. Эквивалентно кривизна может быть вычислена непосредственно на бесконечно малом уровне в терминах скобок Ли поднятых векторных полей.

Соединение 1-форма
Подход Картана и Вейля, использующий 1-формы связности на расслоении фрейма M , дает третий способ понимания римановой связности. Они заметили, что параллельный перенос диктует, что путь на поверхности должен быть поднят до пути в расслоении фрейма так, чтобы его касательные векторы лежали в специальном подпространстве коразмерности один в трехмерном касательном пространстве расслоения фрейма. Проекция на это подпространство определяется дифференциальной 1-формой на ортонормированном расслоении фрейма, формой связности . Это позволило закодировать свойства кривизны поверхности в дифференциальных формах на расслоении фрейма и формулах, включающих их внешние производные .
Этот подход особенно прост для вложенной поверхности. Благодаря результату Кобаяши (1956), 1-форма связности на поверхности, вложенной в евклидово пространство E 3 , является просто обратным протягиванием под отображением Гаусса 1-формы связности на S 2 . [95] Используя отождествление S 2 с однородным пространством SO(3)/SO(2) , 1-форма связности является просто компонентой 1-формы Маурера–Картана на SO(3) . [96]
Глобальная дифференциальная геометрия поверхностей
Хотя характеристика кривизны включает только локальную геометрию поверхности, существуют важные глобальные аспекты, такие как теорема Гаусса–Бонне , теорема униформизации , теорема фон Мангольдта–Адамара и теорема вложимости. Существуют и другие важные аспекты глобальной геометрии поверхностей. [97] К ним относятся:
- Радиус инъективности , определяемый как наибольшее r , такое, что две точки на расстоянии меньше r соединены единственной геодезической. Вильгельм Клингенберг доказал в 1959 году, что радиус инъективности замкнутой поверхности ограничен снизу минимумом δ = π/√ суп К и длина ее наименьшей замкнутой геодезической. Это улучшило теорему Бонне, который в 1855 году показал, что диаметр замкнутой поверхности положительной гауссовой кривизны всегда ограничен сверху δ ; другими словами, геодезическая, реализующая метрическое расстояние между двумя точками, не может иметь длину больше δ .
- Жесткость . В 1927 году Кон-Фоссен доказал, что два овалоида — замкнутые поверхности с положительной гауссовой кривизной — которые изометричны, обязательно конгруэнтны изометрией E 3 . Более того, замкнутая вложенная поверхность с положительной гауссовой кривизной и постоянной средней кривизной обязательно является сферой; аналогично замкнутая вложенная поверхность постоянной гауссовой кривизны должна быть сферой (Либманн 1899). Хайнц Хопф показал в 1950 году, что замкнутая вложенная поверхность с постоянной средней кривизной и родом 0, т. е. гомеоморфная сфере, обязательно является сферой; пять лет спустя Александров снял топологическое предположение. В 1980-х годах Венте построил погруженные торы постоянной средней кривизны в евклидовом 3-пространстве.
- Гипотеза Каратеодори : Эта гипотеза утверждает, что замкнутая выпуклая трижды дифференцируемая поверхность допускает по крайней мере две омбилические точки . Первая работа по этой гипотезе была в 1924 году Гансом Гамбургером , который заметил, что она следует из следующего более сильного утверждения: полуцелочисленный индекс главного кривизны слоения изолированной омбилической поверхности не превышает единицы.
- Нулевая гауссовая кривизна : полная поверхность в E3 с нулевой гауссовой кривизной должна быть цилиндром или плоскостью.
- Теорема Гильберта (1901): никакая полная поверхность с постоянной отрицательной кривизной не может быть изометрически погружена в E 3 .

- Гипотеза Уиллмора . Эта гипотеза утверждает, что интеграл квадрата средней кривизны тора, погруженного в E3 , должен быть ограничен снизу величиной 2π2 . Известно, что интеграл инвариантен относительно Мёбиуса. Она была решена в 2012 году Фернандо Кода Маркесом и Андре Невесом . [98]
- Изопериметрические неравенства . В 1939 году Шмидт доказал, что классическое изопериметрическое неравенство для кривых на евклидовой плоскости справедливо также на сфере или на гиперболической плоскости: а именно, он показал, что среди всех замкнутых кривых, ограничивающих область фиксированной площади, периметр минимизируется, когда кривая является окружностью для метрики. В измерении на одно большее известно, что среди всех замкнутых поверхностей в E 3, возникающих как граница ограниченной области единичного объема, площадь поверхности минимизируется для евклидова шара.
- Систолические неравенства для кривых на поверхностях . Если задана замкнутая поверхность, ее систола определяется как наименьшая длина любой несократимой замкнутой кривой на поверхности. В 1949 году Левнер доказал неравенство тора для метрик на торе, а именно, что площадь тора по квадрату его систолы ограничена снизу √ 3/2 , с равенством в плоском (постоянной кривизны) случае. Аналогичный результат дается неравенством Пу для вещественной проективной плоскости из 1952 года с нижней границей 2/π также достигнуто в случае постоянной кривизны. Для бутылки Клейна Блаттер и Бавард позже получили нижнюю границу √ 8/π . Для замкнутой поверхности рода g Хебда и Бураго показали, что отношение ограничено снизу 1/2 . Три года спустя Михаил Громов нашел нижнюю границу, заданную константой, умноженной на g 1 ⁄ 2 , хотя это не оптимально. Асимптотически точные верхняя и нижняя границы, заданные константами, умноженными на г/(log g ) 2 принадлежат Громову и Бузеру-Сарнаку и могут быть найдены в Katz (2007). Существует также версия для метрик на сфере, принимая за систолу длину наименьшей замкнутой геодезической . Громов предположил нижнюю границу 1/2 √ 3 в 1980 году: лучший результат на данный момент — нижняя граница 1/8 получено Региной Ротман в 2006 году . [99]
Руководство по чтению
Один из наиболее полных вводных обзоров предмета, описывающий историческое развитие от до Гаусса до наших дней, был написан Бергером (2004). Изложения классической теории приведены в работах Эйзенхарта (2004), Крейцига (1991) и Штруика (1988); более современные обильно иллюстрированные учебники для студентов Грея, Аббены и Саламона (2006), Прессли (2001) и Уилсона (2008) могут оказаться более доступными. Доступное изложение классической теории можно найти в работе Гильберта и Кон-Фоссена (1952). Более сложные методы обучения на уровне выпускников, использующие риманову связность на поверхности, можно найти в работах Зингера и Торпа (1967), ду Карму (2016) и О'Нила (2006).
Смотрите также
Примечания
- ^ Гладкая поверхность — это поверхность, на которой каждая точка имеет окрестность, диффеоморфную некоторому открытому множеству в E 2 .
- ^ Риманова поверхность — гладкая поверхность, снабженная римановой метрикой.
- ^ Обратите внимание, что в некоторых более поздних текстах симметричная билинейная форма в правой части называется второй фундаментальной формой; однако в целом она не соответствует классически определенной второй фундаментальной форме.
- ^ Далее следует аргумент, включающий теорему Сакса и Уленбека (1981) об устранимых особенностях гармонических отображений конечной энергии.
- ^ Гаусс 1902.
- ↑ Струик 1987, стр. 50–53.
- ^ Уэллс 2017, стр. 17–30
- ^ Эйлер 1760
- ^ Эйлер 1771
- ^ Крейсциг 1991
- ^ ab Struik 1988
- ^ Уорнер 1983
- ^ Хитчин 2013, стр. 45
- ^ ду Карму 2016, стр. 54–56
- ^ Уилсон 2008, стр. 115
- ^ Пресли 2001, стр. 68–77
- ^ ду Карму 2016, стр. 55
- ^ ду Карму 2016, стр. 60–65
- ^ О'Нил 2006, стр. 113
- ^ Ли «Введение в гладкие многообразия»
- ^ ду Карму 2016, стр. 72
- ^ Крейсциг 1991
- ↑ Сингер и Торп 1967, стр. 100–114.
- ↑ Сингер и Торп 1967, стр. 133–134.
- ^ до Карму, 2016, стр. 155–157.
- ^ Ду Кармо, стр. 235
- ^ Ду Кармо, стр. 238
- ↑ Ду Кармо, страницы 237-238
- ^ Струик 1988, стр. 112
- ↑ Дарбу, том III, стр. 246.
- ^ Бергер. Панорамный вид римановой геометрии.
- ^ О'Нил 2006, стр. 257
- ^ до Карму, 2016, стр. 309–314.
- ^ Хитчин 2013, стр. 57
- ^ ду Карму 2016, стр. 221–222
- ^ О'Нил 2006, стр. 281–289
- ^ Хитчин 2013, стр. 57–58.
- ^ ду Карму 2016, стр. 223
- ^ до Карму, 2016, стр. 222–223.
- ^ до Карму, 2016, стр. 224–225.
- ^ Ду Кармо, стр. 183
- ^ ab Do Carmo, стр. 242
- ^ Хитчин 2013
- ^ Струик 1988
- ^ О'Нил 2006
- ↑ Спивак, «Всеобъемлющее введение в дифференциальную геометрию, т. III», стр. 157.
- ^ Спивак, страницы 161-166
- ^ Спивак, стр. 168
- ^ Эйзенхарт 2004, стр. 228–229
- ^ Эйзенхарт 2004, стр. 241–250; ду Карму, 2016, стр. 188–197.
- ^ ду Карму 2016, стр. 194.
- ^ Эйзенхарт 2004, стр. 61–65.
- ^ abcd Эйзенхарт 2004
- ^ Эйзенхарт 2004, стр. 250–269; ду Карму, 2016, стр. 197–213.
- ^ Решение Дугласа описано в работе Куранта (1950).
- ^ Эйзенхарт 2004, стр. 270–291; О'Нил 2006, стр. 249–251; Гильберт и Кон-Фоссен 1952.
- ↑ Стиллвелл 1996, стр. 1–5.
- ^ Уилсон 2008.
- ^ О'Нил 2006, стр. 195–216; ду Карму 2016, стр. 134–153; Сингер и Торп 1967, стр. 216–224.
- ^ Грей, Аббена и Саламон 2006, с. 386.
- ^ Бергер 2004; Уилсон 2008; Милнор 1963.
- ^ Эйзенхарт 2004, стр. 131; Бергер 2004, стр. 39; ду Карму 2016, стр. 248; О'Нил 2006, стр. 237
- ^ Эйзенхарт 2004; Тейлор 1996a, стр. 472–473, Приложение C.
- ^ Эйзенхарт 2004, раздел 88; Бергер 2004.
- ^ ду Карму 2016, стр. 357
- ^ Милнор 1963
- ^ Уилсон 2008
- ^ ab Бергер 2004
- ^ до Карму, 2016, стр. 303–305.
- ^ Бергер 2004, стр. 41, 61, 123–124
- ^ О'Нил 2006, стр. 395
- ^ Хельгасон 1978, стр. 92
- ^ О'Нил 2006, стр. 286
- ^ ду Карму 2016, стр. 227
- ^ Оссерман 2002, стр. 31–32
- ^ до Карму, 2016, стр. 283–286.
- ^ Торп 1994, стр. 201–207.
- ^ Singer & Thorpe 1967; Garsia, Adriano M. (1961), "Вложение замкнутых римановых поверхностей в евклидово пространство", Comment. Math. Helv. , 35 : 93–110, doi :10.1007/BF02567009, S2CID 120653575
- ^ Имаёси и Танигучи 1992, стр. 47–49.
- ^ Бергер 1977; Тейлор 1996b.
- ^ Уилсон 2008, стр. 1–23, Глава I, Евклидова геометрия .
- ^ ду Карму 2016.
- ^ Уилсон 2008, стр. 25–49, Глава II, Сферическая геометрия .
- ^ Уилсон 2008, Глава 2.
- ^ Эйзенхарт 2004, стр. 110.
- ↑ Стиллвелл 1996; Бонола, Карслоу и Энрикес 1955.
- ^ Уилсон 2008, Глава 5.
- ^ Тейлор 1996b, стр. 107; Бергер 1977, стр. 341–343.
- ↑ Бергер 1977, стр. 222–225; Тейлор 1996b, стр. 101–108.
- ^ Тейлор 1996b
- ^ Чоу 1991
- ↑ Чэнь, Лу и Тянь (2006) указали на недостающий шаг в подходе Гамильтона и Чоу и исправили его; см. также Эндрюс и Брайан (2010).
- ^ Эйзенхарт 2004; Крейциг 1991; Бергер 2004; Уилсон 2008.
- ^ Кобаяши и Номидзу 1969, Глава XII.
- ^ до Карму, 2016; О'Нил, 2006 г.; Сингер и Торп 1967.
- ^ Леви-Чивита 1917
- ^ Арнольд 1989, стр. 301–306, Приложение I.; Бергер 2004, стр. 263–264.
- ^ Дарбу.
- ^ Кобаяси и Номидзу 1969
- ^ Айви и Ландсберг 2003.
- ^ Бергер 2004, стр. 145–161; ду Карму, 2016 г.; Черн 1967; Хопф 1989.
- ^ Кода Маркес, Фернандо; Невес, Андре (2014). «Теория минимума-максимума и гипотеза Уиллмора». Annals of Mathematics . 179 (2): 683–782. arXiv : 1202.6036 . doi : 10.4007/annals.2014.179.2.6. JSTOR 24522767. S2CID 50742102.
- ^ Ротман, Р. (2006) "Длина кратчайшей замкнутой геодезической и площадь двумерной сферы", Proc. Amer. Math. Soc. 134 : 3041-3047. Предыдущие нижние оценки были получены Кроуком, Ротманом-Набутовским и Сабуро.
Ссылки
- Эндрюс, Бен; Брайан, Пол (2010), «Ограничения кривизны с помощью изопериметрического сравнения для нормализованного потока Риччи на двухсфере», Calc. Var. Partial Differential Equations , 39 (3–4): 419–428, arXiv : 0908.3606 , doi : 10.1007/s00526-010-0315-5, S2CID 1095459
- Арнольд, VI (1989), Математические методы классической механики , Graduate Texts in Mathematics, т. 60 (2-е изд.), Нью-Йорк: Springer-Verlag, ISBN 978-0-387-90314-9; перевод с русского К. Фогтмана и А. Вайнштейна.
- Бергер, Марсель (2004), Панорамный вид римановой геометрии , Springer-Verlag, ISBN 978-3-540-65317-2
- Бергер, Мелвин С. (1977), Нелинейность и функциональный анализ , Academic Press, ISBN 978-0-12-090350-4
- Бонола, Роберто; Карслоу, Х.С.; Энрикес, Ф. (1955), Неевклидова геометрия: критическое и историческое исследование ее развития , Довер, ISBN 978-0-486-60027-7
- Бутби, Уильям М. (1986), Введение в дифференцируемые многообразия и риманову геометрию , Чистая и прикладная математика, т. 120 (2-е изд.), Academic Press, ISBN 0121160521
- Картан, Эли (1983), Геометрия римановых пространств, Math Sci Press, ISBN 978-0-915692-34-7; перевод из 2-го издания книги «Leçons sur la géométrie des espaces de Riemann » (1951) Джеймса Глейзбрука.
- Картан, Эли (2001), Риманова геометрия в ортогональной системе отсчета (из лекций, прочитанных Э. Картаном в Сорбонне в 1926-27 гг.), World Scientific, ISBN 978-981-02-4746-1; перевод с русского В. В. Гольдберга с предисловием С. С. Черна .
- Картан, Анри (1971), Calcul Differentiel (на французском), Герман , ISBN 9780395120330
- Чэнь, Сюсюн; Лу, Пэн; Тянь, Ган (2006), «Заметка об униформизации римановых поверхностей потоком Риччи», Proc. AMS , 134 (11): 3391–3393, doi : 10.1090/S0002-9939-06-08360-2
- Черн, СС (1967), Кривые и поверхности в евклидовых пространствах , Исследования MAA по математике, Математическая ассоциация Америки
- Chow, B. (1991), «Поток Риччи на 2-сфере», J. Diff. Geom. , 33 (2): 325–334, doi : 10.4310/jdg/1214446319
- Курант, Ричард (1950), Принцип Дирихле, Конформное отображение и минимальные поверхности , John Wiley & Sons, ISBN 978-0-486-44552-6
- Дарбу, Гастон , «Уроки общей теории поверхностей» , Готье-ВилларТом I (1887), Том II (1915) [1889], Том III (1894), Том IV (1896).
- Дин, В. (2001), «Доказательство теоремы об униформизации на S2 » , Журнал дифференциальных уравнений с частными производными , 14 : 247–250
- до Кармо, Манфредо П. (2016), Дифференциальная геометрия кривых и поверхностей (пересмотренное и обновленное 2-е изд.), Минеола, Нью-Йорк: Dover Publications, Inc., ISBN 978-0-486-80699-0
- ду Кармо, Манфредо (1992), Риманова геометрия , Математика: теория и приложения, Биркхойзер, ISBN 0-8176-3490-8
- Эйзенхарт, Лютер Пфалер (2004), Трактат о дифференциальной геометрии кривых и поверхностей (переиздание издания 1909 года), Dover Publications, Inc., ISBN 0-486-43820-1
- Эйлер, Леонард (1760), «Recherches sur la Courbure des Surfaces», Mémoires de l'Académie des Sciences de Berlin , 16 (опубликовано в 1767 г.): 119–143..
- Эйлер, Леонард (1771), «De Solidis quorum superficiem in planum explicare licet», Novi Commentarii Academiae Scientiarum Petropolitanae , 16 (опубликовано в 1772 г.): 3–34..
- Гаусс, Карл Фридрих (1902), Общие исследования кривых поверхностей 1825 и 1827 годов, Библиотека Принстонского университетаперевод А. М. Хилтебейтеля и Дж. К. Морхеда; «Disquisitiones Generales Circa Superficies Curvas», Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores Vol. VI (1827), стр. 99–146.
- Гаусс, Карл Фридрих (1965), Общие исследования кривых поверхностей , перевод AM Hiltebeitel; JC Morehead, Hewlett, NY: Raven Press, OCLC 228665499.
- Гаусс, Карл Фридрих (2005), Общие исследования криволинейных поверхностей , под редакцией с новым введением и примечаниями Питера Песича, Минеола, Нью-Йорк: Dover Publications, ISBN 978-0-486-44645-5.
- Грей, Альфред; Аббена, Эльза; Саламон, Саймон (2006), Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica® , Исследования по высшей математике (3-е изд.), Бока-Ратон, Флорида: Chapman & Hall/CRC, ISBN 978-1-58488-448-4
- Хан, Цин; Хун, Цзя-Син (2006), Изометрическое вложение римановых многообразий в евклидовы пространства , Американское математическое общество, ISBN 978-0-8218-4071-9
- Хельгасон, Сигурдур (1978), Дифференциальная геометрия, группы Ли и симметричные пространства , Academic Press, Нью-Йорк, ISBN 978-0-12-338460-7
- Гильберт, Дэвид ; Кон-Фоссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, ISBN 978-0-8284-1087-8
- Хитчин, Найджел (2013), Геометрия поверхностей (PDF)
- Хопф, Хайнц (1989), Лекции по дифференциальной геометрии в целом , Lecture Notes in Mathematics, т. 1000, Springer-Verlag, ISBN 978-3-540-51497-8
- Имаёси, Ю.; Танигучи, М. (1992), Введение в пространства Техмюллера , Springer-Verlag, ISBN 978-0-387-70088-5
- Айви, Томас А.; Ландсберг, Дж. М. (2003), Картан для начинающих: Дифференциальная геометрия с использованием подвижных рамок и внешних систем , Исследования в области математики, т. 61, Американское математическое общество, ISBN 978-0-8218-3375-9
- Кац, Михаил Г. (2007), Систолическая геометрия и топология , Математические обзоры и монографии, т. 137, Американское математическое общество, ISBN 978-0-8218-4177-8
- Милнор, Дж. (1963). Теория Морзе . Annals of Mathematics Studies. Том 51. Принстон, Нью-Джерси: Princeton University Press. MR 0163331. Zbl 0108.10401.
- Кобаяси, Сёсичи (1956), «Индуцированные связи и вложенное риманово пространство», Nagoya Math. J. , 10 : 15–25, doi : 10.1017/S0027763000000052
- Кобаяши, Шошичи (1957), «Теория связей», Annali di Matematica Pura ed Applicata , Series 4, 43 : 119–194, doi : 10.1007/BF02411907 , S2CID 120972987,
- Кобаяши, Шошичи; Номидзу, Кацуми (1963), Основы дифференциальной геометрии, Том. Я , Wiley Interscience, ISBN 978-0-470-49648-0
- Кобаяши, Шошичи; Номидзу, Кацуми (1969), Основы дифференциальной геометрии, Том. II , Wiley Interscience, ISBN 978-0-470-49648-0
- Крейциг, Эрвин (1991), Дифференциальная геометрия , Дувр, ISBN 978-0-486-66721-8
- Кюнель, Вольфганг (2006), Дифференциальная геометрия: Кривые - Поверхности - Многообразия , Американское математическое общество, ISBN 978-0-8218-3988-1
- Леви-Чивита, Туллио (1917), «Nozione di Parallismo in una varietà qualunque», Rend. Цирк. Мат. Палермо , 42 : 173–205, номер документа : 10.1007/BF03014898, S2CID 122088291
- О'Нил, Барретт (2006), Элементарная дифференциальная геометрия (пересмотренное 2-е изд.), Амстердам: Elsevier/Academic Press, ISBN 0-12-088735-5
- Осгуд, Б.; Филлипс, Р.; Сарнак, П. (1988), "Экстремали определителей лапласианов", J. Funct. Anal. , 80 : 148–211, doi : 10.1016/0022-1236(88)90070-5
- Оссерман, Роберт (2002), Обзор минимальных поверхностей , Довер, ISBN 978-0-486-49514-9
- Ян Р. Портеус (2001) Геометрическое дифференцирование: для понимания кривых и поверхностей , Cambridge University Press ISBN 0-521-00264-8 .
- Пресли, Эндрю (2001), Элементарная дифференциальная геометрия , Springer Undergraduate Mathematics Series, Springer-Verlag, ISBN 978-1-85233-152-8
- Сакс, Дж.; Уленбек, Карен (1981), «Существование минимальных погружений 2-сфер», Ann. of Math. , 112 (1): 1–24, doi :10.2307/1971131, JSTOR 1971131
- Сингер, Изадор М.; Торп, Джон А. (1967), Конспект лекций по элементарной топологии и геометрии , Springer-Verlag, ISBN 978-0-387-90202-9
- Спивак, Майкл (1965), Исчисление на многообразиях. Современный подход к классическим теоремам продвинутого исчисления , WA Benjamin
- Стиллвелл, Джон (1996), Источники гиперболической геометрии , Американское математическое общество, ISBN 978-0-8218-0558-9
- Струик, Дирк (1987), Краткая история математики (4-е изд.), Dover Publications, ISBN 0486602559
- Струик, Дирк Дж. (1988) [1961], Лекции по классической дифференциальной геометрии (переиздание 2-го изд.), Нью-Йорк: Dover Publications, Inc., ISBN 0-486-65609-8
- Тейлор, Майкл Э. (1996a), Уравнения с частными производными II: Качественные исследования линейных уравнений , Springer-Verlag, ISBN 978-1-4419-7051-0
- Тейлор, Майкл Э. (1996b), Уравнения в частных производных III: Нелинейные уравнения , Springer-Verlag, ISBN 978-1-4419-7048-0
- Торп, Джон А. (1994), Элементарные темы дифференциальной геометрии , Тексты для бакалавров по математике, Springer-Verlag, ISBN 0387903577
- Топоногов, Виктор А. (2005), Дифференциальная геометрия кривых и поверхностей: Краткое руководство , Springer-Verlag, ISBN 978-0-8176-4384-3
- Валирон, Жорж (1986), Классическая дифференциальная геометрия кривых и поверхностей , Math Sci Press, ISBN 978-0-915692-39-2Полный текст книги
- Уорнер, Фрэнк В. (1983), Основы дифференцируемых многообразий и групп Ли , Graduate Texts in Mathematics, т. 94, Springer, ISBN 0-387-90894-3
- Уэллс, РО (2017), Дифференциальная и комплексная геометрия: истоки, абстракции и вложения , Springer, ISBN 9783319581842
- Уилсон, Пелхэм (2008), Искривленное пространство: от классических геометрий к элементарной дифференциальной геометрии , Cambridge University Press, ISBN 978-0-521-71390-0





















![{\displaystyle [X,Y]=XY-YX}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838f73010b4f791eeaf245317fb4b6e07c45d741)
![{\displaystyle [X,Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94470b44d283fde62130212956058ca6b727da37)
![{\displaystyle [X,Y]=-[Y,X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c433e248c0c7e659ef3f2d9df64d8c7505630bc)
![{\displaystyle [[X,Y],Z]+[[Y,Z],X]+[[Z,X],Y]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d5d5018bd0a276d74259b92a5403824cd982e7)













































































![{\displaystyle K=-{\beta ^{2} \over ((s-\alpha )^{2}+\beta ^{2})^{2}},\,\,K_{m}=-{r[(s-\alpha )^{2}+\beta ^{2})]+\beta _{t}(s-\alpha )+\beta \alpha _{t} \over [(s-\alpha )^{2}+\beta ^{2}]^{\frac {3}{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff1ab2130e1d570ae5585c216637fb7661847192)








![{\displaystyle K=-{1 \over 2H}\left[\partial _{x}\left({\frac {G_{x}}{H}}\right)+\partial _{y}\left({\frac {E_{y}}{H}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa6e6e49b1e0f474132e77018b4d8a8fc78a853d)


































