Полярная система координат

В математике полярная система координат — это двумерная система координат , в которой каждая точка на плоскости определяется расстоянием от точки отсчета и углом от направления отсчета. Точка отсчета (аналогично началу декартовой системы координат ) называется полюсом , а луч от полюса в направлении отсчета — полярной осью . Расстояние от полюса называется радиальной координатой , радиальным расстоянием или просто радиусом , а угол называется угловой координатой , полярным углом или азимутом . [1] Углы в полярной нотации обычно выражаются либо в градусах , либо в радианах (2 π рад равно 360°).
Грегуар де Сен-Венсан и Бонавентура Кавальери независимо друг от друга ввели эти концепции в середине XVII века, хотя сам термин «полярные координаты» приписывается Грегорио Фонтане в XVIII веке. Первоначальной мотивацией для введения полярной системы было изучение кругового и орбитального движения .
Полярные координаты наиболее уместны в любом контексте, где рассматриваемое явление по своей сути связано с направлением и длиной от центральной точки на плоскости, например, спирали . Плоские физические системы с телами, движущимися вокруг центральной точки, или явления, происходящие из центральной точки, часто проще и интуитивно понятнее моделировать с использованием полярных координат.
Полярная система координат расширена на три измерения двумя способами: цилиндрическая и сферическая системы координат.
История
.jpg/440px-Head_of_Hipparchus_(cropped).jpg)
Понятия угла и радиуса использовались уже древними народами первого тысячелетия до нашей эры . Греческий астроном и астролог Гиппарх (190–120 гг. до н. э.) создал таблицу функций хорды , дающую длину хорды для каждого угла, и есть ссылки на то, что он использовал полярные координаты для установления положений звезд. [2] В работе «О спиралях » Архимед описывает архимедову спираль , функцию, радиус которой зависит от угла. Однако греческая работа не распространялась на полную систему координат.
Начиная с 8-го века нашей эры астрономы разрабатывали методы аппроксимации и вычисления направления на Мекку ( киблу ) — и расстояния до нее — из любого места на Земле. [3] Начиная с 9-го века они использовали сферическую тригонометрию и методы картографической проекции для точного определения этих величин. Расчет по сути представляет собой преобразование экваториальных полярных координат Мекки (т. е. ее долготы и широты ) в ее полярные координаты (т. е. ее киблу и расстояние) относительно системы, чей референтный меридиан — это большой круг, проходящий через заданное местоположение и полюса Земли, а полярная ось — это линия, проходящая через местоположение и его антиподную точку . [4]
Существуют различные отчеты о введении полярных координат как части формальной системы координат. Полная история предмета описана в работе профессора Гарварда Джулиана Лоуэлла Кулиджа « Происхождение полярных координат». [5] Грегуар де Сен-Винсент и Бонавентура Кавальери независимо друг от друга ввели эти концепции в середине семнадцатого века. Сен-Винсент писал о них в частном порядке в 1625 году и опубликовал свою работу в 1647 году, в то время как Кавальери опубликовал свою в 1635 году с исправленной версией, появившейся в 1653 году. Кавальери впервые использовал полярные координаты для решения задачи, касающейся площади внутри спирали Архимеда . Впоследствии Блез Паскаль использовал полярные координаты для вычисления длины параболических дуг .
В «Методе флюксий» (написанном в 1671 г., опубликованном в 1736 г.) сэр Исаак Ньютон исследовал преобразования между полярными координатами, которые он назвал «Седьмым способом; для спиралей», и девятью другими системами координат. [6] В журнале Acta Eruditorum (1691 г.) Якоб Бернулли использовал систему с точкой на линии, называемой полюсом и полярной осью соответственно. Координаты задавались расстоянием от полюса и углом от полярной оси . Работа Бернулли распространилась на нахождение радиуса кривизны кривых, выраженных в этих координатах.
Фактический термин полярные координаты приписывается Грегорио Фонтане и использовался итальянскими писателями 18-го века. Термин появился в английском языке в переводе Джорджа Пикока 1816 года «Дифференциального и интегрального исчисления» Лакруа . [ 7] [8] Алексис Клеро был первым, кто задумался о полярных координатах в трех измерениях, а Леонард Эйлер был первым, кто фактически разработал их. [5]
Конвенции

Радиальная координата часто обозначается как r или ρ , а угловая координата как φ , θ или t . Угловая координата определяется как φ по стандарту ISO 31-11 . Однако в математической литературе угол часто обозначается как θ.
Углы в полярной системе обозначений обычно выражаются в градусах или радианах (2π рад равен 360°). Градусы традиционно используются в навигации , геодезии и многих прикладных дисциплинах, тогда как радианы более распространены в математике и математической физике . [9]
Угол φ определяется как начинающийся с 0° от опорного направления и увеличивающийся для вращений в направлении по часовой стрелке (cw) или против часовой стрелки (ccw). Например, в математике опорное направление обычно рисуется как луч от полюса горизонтально вправо, а полярный угол увеличивается до положительных углов для вращений ccw, тогда как в навигации ( пеленг , курс ) 0°-курс рисуется вертикально вверх, а угол увеличивается для вращений cw. Полярные углы уменьшаются до отрицательных значений для вращений в соответственно противоположных ориентациях.
Уникальность полярных координат
Добавление любого количества полных оборотов (360°) к угловой координате не меняет соответствующего направления. Аналогично, любая полярная координата идентична координате с отрицательной радиальной составляющей и противоположным направлением (добавление 180° к полярному углу). Поэтому одна и та же точка ( r , φ ) может быть выражена бесконечным числом различных полярных координат ( r , φ + n × 360°) и (− r , φ + 180° + n × 360°) = (− r , φ + (2 n + 1) × 180°) , где n — произвольное целое число . [10] Более того, сам полюс может быть выражен как (0, φ ) для любого угла φ . [11]
Если для любой точки, кроме полюса, требуется уникальное представление, обычно r ограничивают положительными числами ( r > 0 ), а φ — либо интервалом [0, 360°) , либо интервалом (−180°, 180°] , что в радианах равно [0, 2π) или (−π, π] . [12] Другое соглашение, касающееся обычной области значений функции arctan , заключается в том, чтобы допускать произвольные ненулевые действительные значения радиальной составляющей и ограничивать полярный угол до (−90°, 90°] . Во всех случаях необходимо выбрать уникальный азимут для полюса ( r = 0), например, φ = 0.
Преобразование между полярными и декартовыми координатами
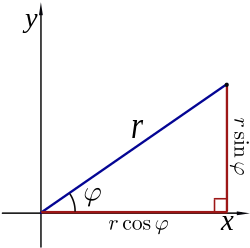
Полярные координаты r и φ можно преобразовать в декартовы координаты x и y, используя тригонометрические функции синуса и косинуса:
Декартовы координаты x и y можно преобразовать в полярные координаты r и φ , где r ≥ 0, а φ находится в интервале (− π , π ] по формуле: [13] где hypot — это пифагорова сумма , а atan2 — это обычная вариация функции арктангенса, определяемая как
Если сначала вычислить r , как указано выше, то эту формулу для φ можно сформулировать проще, используя функцию арккосинуса :
Комплексные числа
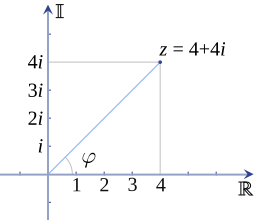
Каждое комплексное число можно представить в виде точки на комплексной плоскости и, следовательно, выразить, указав либо декартовы координаты точки (называемые прямоугольной или декартовой формой), либо полярные координаты точки (называемые полярной формой).
В полярной форме координаты расстояния и угла часто называют величиной и аргументом числа соответственно. Два комплексных числа можно умножить, сложив их аргументы и умножив их величины.
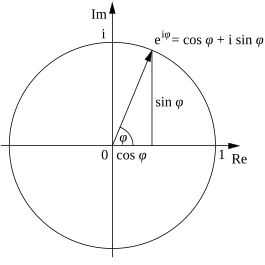
Комплексное число z может быть представлено в прямоугольной форме как , где i - мнимая единица , или может быть альтернативно записано в полярной форме как и оттуда, по формуле Эйлера , [14] как , где e - число Эйлера , а φ , выраженное в радианах, является главным значением функции комплексного числа arg , примененной к x + iy . Для преобразования между прямоугольной и полярной формами комплексного числа можно использовать приведенные выше формулы преобразования. Эквивалентными являются цис- и угловые обозначения :
Для операций умножения , деления , возведения в степень и извлечения корня комплексных чисел, как правило, гораздо проще работать с комплексными числами, выраженными в полярной форме, а не в прямоугольной. Из законов возведения в степень:
- Умножение
- Разделение
- Возведение в степень ( формула Муавра )
- Извлечение корня (главный корень)
Полярное уравнение кривой
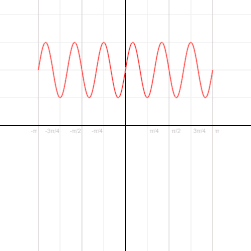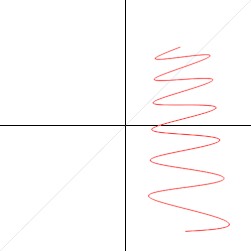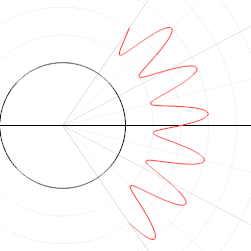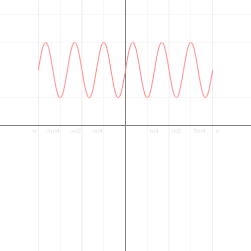
Уравнение, определяющее плоскую кривую, выраженную в полярных координатах, известно как полярное уравнение . Во многих случаях такое уравнение можно просто задать, определив r как функцию φ . Полученная кривая затем состоит из точек вида ( r ( φ ), φ ) и может рассматриваться как график полярной функции r . Обратите внимание, что, в отличие от декартовых координат, независимая переменная φ является второй записью в упорядоченной паре.
Различные формы симметрии можно вывести из уравнения полярной функции r :
- Если r (− φ ) = r ( φ ), кривая будет симметрична относительно горизонтального луча (0°/180°);
- Если r ( π − φ ) = r ( φ ), то он будет симметричен относительно вертикального луча (90°/270°):
- Если r ( φ − α) = r ( φ ), то он будет вращательно-симметричным относительно α по часовой стрелке и против часовой стрелки вокруг полюса.
Из-за круговой природы полярной системы координат многие кривые можно описать довольно простым полярным уравнением, тогда как их декартова форма гораздо более сложна. Среди наиболее известных из этих кривых — полярная роза , архимедова спираль , лемниската , улитка и кардиоида .
Для окружности, линии и полярной розы, представленных ниже, подразумевается, что ограничений на область определения и диапазон кривой нет.
Круг
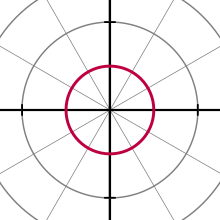
Общее уравнение для окружности с центром в точке и радиусом a имеет вид
Это можно упростить различными способами, чтобы оно соответствовало более конкретным случаям, таким как уравнение для окружности с центром в полюсе и радиусом a . [15]
Когда r 0 = a или начало координат лежит на окружности, уравнение принимает вид
В общем случае уравнение можно решить относительно r , получив Решение со знаком минус перед квадратным корнем дает ту же кривую.
Линия
Радиальные линии (проходящие через полюс) представлены уравнением где - угол возвышения линии; то есть, , где - наклон линии в декартовой системе координат. Нерадиальная линия, которая пересекает радиальную линию перпендикулярно в точке, имеет уравнение
Иначе говоря, это точка, в которой касательная пересекает воображаемую окружность радиуса
Полярная роза

Полярная роза — это математическая кривая, которая выглядит как цветок с лепестками и может быть выражена простым полярным уравнением:
для любой константы γ 0 (включая 0). Если k — целое число, эти уравнения дадут k -лепестковую розу, если k — нечетное число , или 2 k -лепестковую розу, если k — четное число. Если k — рациональное, но не целое число, может образоваться розоподобная форма, но с перекрывающимися лепестками. Обратите внимание, что эти уравнения никогда не определяют розу с 2, 6, 10, 14 и т. д. лепестками. Переменная a напрямую представляет длину или амплитуду лепестков розы, в то время как k относится к их пространственной частоте. Константу γ 0 можно рассматривать как фазовый угол.
Архимедова спираль

Архимедова спираль — это спираль, открытая Архимедом , которую также можно выразить в виде простого полярного уравнения. Она представлена уравнением Изменение параметра a повернет спираль, в то время как b управляет расстоянием между плечами, которое для данной спирали всегда постоянно. Архимедова спираль имеет два плеча, одно для φ > 0 и одно для φ < 0. Два плеча плавно соединены на полюсе. Если a = 0 , то зеркальное отображение одного плеча поперек линии 90°/270° даст другое плечо. Эта кривая примечательна как одна из первых кривых, после конических сечений , описанных в математическом трактате, и как яркий пример кривой, наилучшим образом определяемой полярным уравнением.
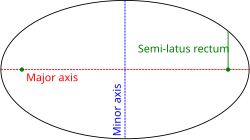
Конические сечения
Коническое сечение с одним фокусом на полюсе, а другим где-то на луче 0° (так что большая ось конического сечения лежит вдоль полярной оси) задается как: где e — эксцентриситет , а — полуширота прямой (перпендикулярное расстояние в фокусе от большой оси до кривой). Если e > 1 , это уравнение определяет гиперболу ; если e = 1 , оно определяет параболу ; и если e < 1 , оно определяет эллипс . Частный случай последнего, e = 0, приводит к окружности радиуса .
Квадратрикс

Квадратриса в первом квадранте ( x, y ) — это кривая с y = ρ sin θ, равная доле четверти окружности с радиусом r , определяемой радиусом, проходящим через точку кривой. Поскольку эта доля равна , кривая задается как . [16]
Пересечение двух полярных кривых
Графики двух полярных функций имеют возможные пересечения трех типов:
- В начале координат, если уравнения и имеют хотя бы одно решение каждое.
- Все точки , где являются решениями уравнения , где — целое число.
- Все точки , где являются решениями уравнения , где — целое число.
Исчисление
Исчисление можно применять к уравнениям, выраженным в полярных координатах. [17] [18]
Угловая координата φ в этом разделе выражается в радианах, что является общепринятым выбором при выполнении вычислений.
Дифференциальное исчисление
Используя x = r cos φ и y = r sin φ , можно вывести соотношение между производными в декартовых и полярных координатах. Для заданной функции u ( x , y ) следует, что (вычисляя ее полные производные ) или
Следовательно, имеем следующие формулы:
Используя обратное преобразование координат, можно вывести аналогичное обратное соотношение между производными. При наличии функции u ( r , φ ) следует, что или
Следовательно, имеем следующие формулы:
Чтобы найти декартов наклон касательной к полярной кривой r ( φ ) в любой заданной точке, кривая сначала выражается в виде системы параметрических уравнений .
Дифференцируя оба уравнения по φ, получаем
Разделив второе уравнение на первое, получаем декартов наклон касательной к кривой в точке ( r ( φ ), φ ) :
Другие полезные формулы, включая дивергенцию, градиент и Лапласиан в полярных координатах, см. в разделе Криволинейные координаты .
Интегральное исчисление (длина дуги)
Длина дуги (длина отрезка прямой), определяемая полярной функцией, находится путем интегрирования по кривой r ( φ ). Пусть L обозначает эту длину вдоль кривой, начинающуюся от точек A до точки B , где эти точки соответствуют φ = a и φ = b таким образом, что 0 < b − a < 2 π . Длина L задается следующим интегралом
Интегральное исчисление (площадь)
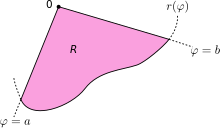
Пусть R обозначает область, ограниченную кривой r ( φ ) и лучами φ = a и φ = b , где 0 < b − a ≤ 2 π . Тогда площадь R равна
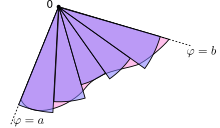

Этот результат можно найти следующим образом. Сначала интервал [ a , b ] делится на n подынтервалов, где n — некоторое положительное целое число. Таким образом, Δ φ , угловая мера каждого подынтервала, равна b − a (общая угловая мера интервала), деленная на n , количество подынтервалов. Для каждого подынтервала i = 1, 2, ..., n пусть φ i будет средней точкой подынтервала и построим сектор с центром в полюсе, радиусом r ( φ i ), центральным углом Δ φ и длиной дуги r ( φ i )Δ φ . Площадь каждого построенного сектора, таким образом, равна Следовательно, общая площадь всех секторов равна
По мере увеличения числа подынтервалов n аппроксимация площади улучшается. Принимая n → ∞ , сумма становится суммой Римана для вышеуказанного интеграла.
Механическим устройством, вычисляющим интегралы площади, является планиметр , который измеряет площадь плоских фигур, обводя их: это воспроизводит интегрирование в полярных координатах путем добавления шарнира, так что двухэлементная связь выполняет теорему Грина , преобразуя квадратичный полярный интеграл в линейный интеграл.
Обобщение
Используя декартовы координаты , бесконечно малый элемент площади можно вычислить как dA = dx dy . Правило подстановки для кратных интегралов гласит, что при использовании других координат необходимо учитывать определитель Якоби формулы преобразования координат:
Следовательно, элемент площади в полярных координатах можно записать как
Теперь функцию, заданную в полярных координатах, можно проинтегрировать следующим образом:
Здесь R — та же область, что и выше, а именно, область, ограниченная кривой r ( φ ) и лучами φ = a и φ = b . Формула для площади R получается путем тождественного приравнивания f к 1.

Более удивительное применение этого результата дает гауссовский интеграл :
Векторные исчисления
Векторные исчисления можно также применять к полярным координатам. Для плоского движения пусть будет вектором положения ( r cos( φ ), r sin( φ )) , где r и φ зависят от времени t .
Мы определяем ортонормальный базис с тремя единичными векторами: радиальным, поперечным и нормальным направлениями . Радиальное направление определяется путем нормализации : Радиальные и скоростные направления охватывают плоскость движения , нормальное направление которой обозначается : Поперечное направление перпендикулярно как радиальному, так и нормальному направлениям:
Затем
Это уравнение можно получить, взяв производную функции и производные единичных базисных векторов.
Для кривой в 2D, где параметром является , предыдущие уравнения упрощаются до:
Центробежные и кориолисовы условия
Термин иногда называют центростремительным ускорением , а термин — ускорением Кориолиса . Например, см. Шанкар. [19]
Примечание: эти термины, которые появляются, когда ускорение выражается в полярных координатах, являются математическим следствием дифференциации; они появляются всякий раз, когда используются полярные координаты. В динамике плоских частиц эти ускорения появляются при установлении второго закона движения Ньютона во вращающейся системе отсчета. Здесь эти дополнительные термины часто называют фиктивными силами ; фиктивными, потому что они просто являются результатом изменения системы координат. Это не означает, что их не существует, скорее они существуют только во вращающейся системе.
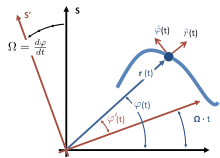
Рама совместного вращения
Для частицы, движущейся плоско, один из подходов к приданию физического значения этим терминам основан на концепции мгновенной совместно вращающейся системы отсчета . [20] Чтобы определить совместно вращающуюся систему отсчета, сначала выбирается начало координат, от которого определяется расстояние r ( t ) до частицы. Устанавливается ось вращения, перпендикулярная плоскости движения частицы и проходящая через это начало координат. Затем в выбранный момент t скорость вращения совместно вращающейся системы Ω приводится в соответствие со скоростью вращения частицы вокруг этой оси, dφ / dt . Затем члены в ускорении в инерциальной системе отсчета связаны с членами в совместно вращающейся системе отсчета. Пусть местоположение частицы в инерциальной системе отсчета будет ( r ( t ), φ ( t )), а в совместно вращающейся системе отсчета будет ( r ′(t), φ ′(t) ). Поскольку вращающаяся совместно система отсчета вращается с той же скоростью, что и частица, dφ ′/ dt = 0. Фиктивная центробежная сила в вращающейся совместно системе отсчета равна mr Ω 2 , радиально наружу. Скорость частицы в вращающейся совместно системе отсчета также радиально наружу, поскольку dφ ′/ dt = 0. Фиктивная сила Кориолиса , следовательно, имеет значение −2 m ( dr / dt )Ω, направленное только в сторону увеличения φ . Таким образом, используя эти силы во втором законе Ньютона, мы находим: где над точками представлены производные по времени, а F — чистая действительная сила (в отличие от фиктивных сил). С точки зрения компонентов это векторное уравнение становится: что можно сравнить с уравнениями для инерциальной системы отсчета:
Это сравнение, а также признание того, что по определению совместно вращающейся системы отсчета в момент времени t она имеет скорость вращения Ω = dφ / dt , показывает, что мы можем интерпретировать члены ускорения (умноженные на массу частицы), найденные в инерциальной системе отсчета, как отрицательные значения центробежной и кориолисовой сил, которые наблюдались бы в мгновенной неинерциальной совместно вращающейся системе отсчета.
Для общего движения частицы (в отличие от простого кругового движения) центробежные и кориолисовы силы в системе отсчета частицы обычно относятся к мгновенной соприкасающейся окружности ее движения, а не к фиксированному центру полярных координат. Для получения более подробной информации см. центростремительная сила .
Дифференциальная геометрия
В современной терминологии дифференциальной геометрии полярные координаты предоставляют координатные карты для дифференцируемого многообразия R 2 \ {(0,0)} , плоскости за вычетом начала координат. В этих координатах евклидов метрический тензор задается как Это можно увидеть с помощью формулы замены переменных для метрического тензора или путем вычисления дифференциальных форм dx , dy через внешнюю производную 0-форм x = r cos( θ ) , y = r sin( θ ) и подстановки их в евклидов метрический тензор ds 2 = dx 2 + dy 2 .
Элементарное доказательство формулы |
|---|
Пусть , и — две точки на плоскости, заданные их декартовыми и полярными координатами. Тогда Так как , и , то получаем, что Теперь воспользуемся тригонометрическим тождеством, чтобы продолжить: Если радиальные и угловые величины близки друг к другу, и, следовательно, близки к общей величине и , то имеем, что . Более того, косинус можно аппроксимировать рядом Тейлора косинуса с точностью до линейных членов: так что , и . Таким образом, вокруг бесконечно малой области любой точки, как и было заявлено. |
Ортонормированный фрейм относительно этой метрики задается с дуальным кофреймом Форма связи относительно этого фрейма и связности Леви-Чивиты задается кососимметричной матрицей 1-форм и, следовательно, форма кривизны Ω = dω + ω ∧ ω исчезает. Поэтому, как и ожидалось, проколотая плоскость является плоским многообразием .
Расширения в 3D
Полярная система координат расширена в трех измерениях с помощью двух различных систем координат: цилиндрической и сферической .
Приложения
Полярные координаты двумерны, и поэтому их можно использовать только там, где положения точек лежат на одной двумерной плоскости. Они наиболее уместны в любом контексте, где рассматриваемое явление по своей сути связано с направлением и длиной от центральной точки. Например, приведенные выше примеры показывают, как элементарных полярных уравнений достаточно для определения кривых, таких как архимедова спираль, уравнение которой в декартовой системе координат было бы гораздо более сложным. Более того, многие физические системы, такие как те, которые связаны с телами, движущимися вокруг центральной точки, или с явлениями, происходящими из центральной точки, проще и интуитивно понятнее для моделирования с использованием полярных координат. Первоначальной мотивацией для введения полярной системы было изучение кругового и орбитального движения .
Положение и навигация
Полярные координаты часто используются в навигации, поскольку пункт назначения или направление движения могут быть заданы как угол и расстояние от рассматриваемого объекта. Например, самолеты используют слегка измененную версию полярных координат для навигации. В этой системе, которая обычно используется для любого вида навигации, луч 0° обычно называется направлением 360, и углы продолжаются по часовой стрелке, а не против часовой стрелки, как в математической системе. Направление 360 соответствует магнитному северу , в то время как направления 90, 180 и 270 соответствуют магнитным востоку, югу и западу соответственно. [21] Таким образом, самолет, летящий на 5 морских миль на восток, будет летать на 5 единиц по направлению 90 (читается как ноль-девять-ноль по данным управления воздушным движением ). [22]
Моделирование
Системы, демонстрирующие радиальную симметрию , обеспечивают естественные настройки для полярной системы координат, при этом центральная точка действует как полюс. Ярким примером такого использования является уравнение потока грунтовых вод , применяемое к радиально-симметричным скважинам. Системы с радиальной силой также являются хорошими кандидатами для использования полярной системы координат. Эти системы включают гравитационные поля , которые подчиняются закону обратных квадратов , а также системы с точечными источниками , такими как радиоантенны .
Радиально асимметричные системы также могут быть смоделированы с помощью полярных координат. Например, диаграмма направленности микрофона иллюстрирует его пропорциональный ответ на входящий звук с заданного направления, и эти диаграммы могут быть представлены в виде полярных кривых. Кривая для стандартного кардиоидного микрофона, наиболее распространенного однонаправленного микрофона, может быть представлена как r = 0,5 + 0,5sin( ϕ ) на его целевой расчетной частоте. [23] Диаграмма смещается в сторону всенаправленности на более низких частотах.
Смотрите также
- Криволинейные координаты
- Список распространённых преобразований координат
- Лог-полярные координаты
- Полярное разложение
- Единичная окружность
Ссылки
- ^ Браун, Ричард Г. (1997). Эндрю М. Глисон (ред.). Продвинутая математика: Предварительные вычисления с дискретной математикой и анализом данных. Эванстон, Иллинойс: McDougal Littell. ISBN 0-395-77114-5.
- ^ Дружелюбный, Майкл (24 августа 2009 г.). «Вехи в истории тематической картографии, статистической графики и визуализации данных» (PDF) . Архивировано из оригинала (PDF) 26 сентября 2018 г. . Получено 23 июля 2016 г. .
- ^ Кинг, Дэвид А. (2005). «Священная география ислама». В Koetsier, Teun; Luc, Bergmans (ред.). Математика и божественное: историческое исследование . Амстердам: Elsevier. стр. 162–78. ISBN 0-444-50328-5.
- ^ Кинг (2005, стр. 169). Расчеты были настолько точными, насколько это было возможно при ограничениях, налагаемых их предположением, что Земля — идеальная сфера.
- ^ ab Coolidge, Julian (1952). «Происхождение полярных координат». American Mathematical Monthly . 59 (2). Математическая ассоциация Америки: 78–85. doi :10.2307/2307104. JSTOR 2307104.
- ^ Boyer, CB (1949). «Ньютон как создатель полярных координат». American Mathematical Monthly . 56 (2). Математическая ассоциация Америки: 73–78. doi :10.2307/2306162. JSTOR 2306162.
- ^ Миллер, Джефф. "Самые ранние известные применения некоторых слов математики" . Получено 10 сентября 2006 г.
- ^ Смит, Дэвид Юджин (1925). История математики, т. II . Бостон: Ginn and Co., стр. 324.
- ^ Serway, Raymond A.; Jewett Jr., John W. (2005). Принципы физики . Brooks/Cole—Thomson Learning. ISBN 0-534-49143-X.
- ^ "Polar Coordinates and Graphing" (PDF) . 2006-04-13. Архивировано из оригинала (PDF) 22 августа 2016 г. Получено 2006-09-22 .
- ^ Ли, Теодор; Дэвид Коэн; Дэвид Склар (2005). Precalculus: With Unit-Circle Trigonometry (Четвертое изд.). Thomson Brooks/Cole. ISBN 0-534-40230-5.
- ^ Стюарт, Ян; Дэвид Толл (1983). Комплексный анализ (путеводитель по самолету для путешествующих автостопом) . Cambridge University Press. ISBN 0-521-28763-4.
- ^ Торренс, Брюс Фоллетт; Ив Торренс (1999). Введение в Mathematica для студентов . Cambridge University Press. ISBN 0-521-59461-8.
- ^ Смит, Джулиус О. (2003). «Тождество Эйлера». Математика дискретного преобразования Фурье (ДПФ) . Издательство W3K. ISBN 0-9745607-0-7. Архивировано из оригинала 2006-09-15 . Получено 2006-09-22 .
- ^ Claeys, Johan. "Polarordinates". Архивировано из оригинала 2006-04-27 . Получено 2006-05-25 .
- ^ NH Lucas, PJ Bunt & JD Bedient (1976) Исторические корни элементарной математики , стр. 113
- ^ Хаш, Лоуренс С. "Области, ограниченные полярными кривыми". Архивировано из оригинала 2000-03-01 . Получено 2006-11-25 .
- ^ Лоуренс С. Хаш. "Касательные линии к полярным графикам". Архивировано из оригинала 21.11.2019 . Получено 25.11.2006 .
- ^ Рамамурти Шанкар (1994). Принципы квантовой механики (2-е изд.). Спрингер. п. 81. ИСБН 0-306-44790-8.
- ^ Для дальнейшего обсуждения см. John R Taylor (2005). Классическая механика . University Science Books. стр. §9.10, стр. 358–359. ISBN 1-891389-22-X.
- ^ Санти, Самрит. "Система навигации самолета" . Получено 26.11.2006 .
- ^ "Чрезвычайные процедуры" (PDF) . Архивировано из оригинала (PDF) 2013-06-03 . Получено 2007-01-15 .
- ^ Эргл, Джон (2005). Справочник звукозаписывающей техники (Четвертое издание). Springer. ISBN 0-387-28470-2.
Общие ссылки
- Адамс, Роберт; Кристофер Эссекс (2013). Исчисление: полный курс (Восьмое изд.). Pearson Canada Inc. ISBN 978-0-321-78107-9.
- Антон, Ховард; Айрл Бивенс; Стивен Дэвис (2002). Исчисление (седьмое изд.). Anton Textbooks, Inc. ISBN 0-471-38157-8.
- Finney, Ross; George Thomas; Franklin Demana; Bert Waits (июнь 1994 г.). Calculus: Graphical, Numerical, Algebraic (ред. версии с одной переменной). Addison-Wesley Publishing Co. ISBN 0-201-55478-X.
Внешние ссылки
- «Полярные координаты», Энциклопедия математики , EMS Press , 2001 [1994]
- Преобразователь координат — преобразует полярные, декартовы и сферические координаты.
- Динамическая демонстрация полярной системы координат











![{\displaystyle {\sqrt[{n}]{re^{i\varphi }}} = {\sqrt[{n}]{r}}e^{i\varphi \over n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9702297c60884f24c748553ecc7246eccf95a448)
























![{\displaystyle [g(\theta _{i}),\theta _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c3942e962cea54fd104a33ebac17dde8bffa819)




![{\displaystyle {\begin{aligned}r{\frac {du}{dr}}&=r{\frac {\partial u}{\partial x}}\cos \varphi +r{\frac {\partial u}{\partial y}}\sin \varphi =x{\frac {\partial u}{\partial x}}+y{\frac {\partial u}{\partial y}},\\[2pt]{\frac {du}{d\varphi }}&=-{\frac {\partial u}{\partial x}}r\sin \varphi +{\frac {\partial u}{\partial y}}r\cos \varphi =-y{\frac {\partial u}{\partial x}}+x{\frac {\partial u}{\partial y}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01d876b55918333fa5b3792a72f5254b82b86c63)
![{\displaystyle {\begin{align}r{\frac {d}{dr}}&=x{\frac {\partial }{\partial x}}+y{\frac {\partial }{\partial y}}\\[2pt]{\frac {d}{d\varphi }}&=-y{\frac {\partial }{\partial x}}+x{\frac {\partial }{\partial y}}.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f6d6d1a9e05c093275ecaf66033a4298e41fe1d)
![{\displaystyle {\begin{align}{\frac {du}{dx}}&={\frac {\partial u}{\partial r}}{\frac {\partial r}{\partial x}}+{\frac {\partial u}{\partial \varphi }}{\frac {\partial \varphi }{\partial x}},\\[2pt]{\frac {du}{dy}}&={\frac {\partial u}{\partial r}}{\frac {\partial r}{\partial y}}+{\frac {\partial u}{\partial \varphi }}{\frac {\partial \varphi }{\partial y}},\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f446e4f0df07ead889d7039cec3301472fc1f9ea)
![{\displaystyle {\begin{aligned}{\frac {du}{dx}}&={\frac {\partial u}{\partial r}}{\frac {x}{\sqrt {x^{2}+y^{2}}}}-{\frac {\partial u}{\partial \varphi }}{\frac {y}{x^{2}+y^{2}}}\\[2pt]&=\cos \varphi {\frac {\partial u}{\partial r}}-{\frac {1}{r}}\sin \varphi {\frac {\partial u}{\partial \varphi }},\\[2pt]{\frac {du}{dy}}&={\frac {\partial u}{\partial r}}{\frac {y}{\sqrt {x^{2}+y^{2}}}}+{\frac {\partial u}{\partial \varphi }}{\frac {x}{x^{2}+y^{2}}}\\[2pt]&=\sin \varphi {\frac {\partial u}{\partial r}}+{\frac {1}{r}}\cos \varphi {\frac {\partial u}{\partial \varphi }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dcc66ee6a6250cc206f488bb56f976a9a8bd2e8)
![{\displaystyle {\begin{align}{\frac {d}{dx}}&=\cos \varphi {\frac {\partial }{\partial r}}-{\frac {1}{r}}\sin \varphi {\frac {\partial }{\partial \varphi }}\\[2pt]{\frac {d}{dy}}&=\sin \varphi {\frac {\partial }{\partial r}}+{\frac {1}{r}}\cos \varphi {\frac {\partial }{\partial \varphi }}.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a08bfe016a4d8e15a933032d077bcdf8c49d41e)

![{\displaystyle {\begin{aligned}{\frac {dx}{d\varphi }}&=r'(\varphi)\cos \varphi -r(\varphi)\sin \varphi \\[2pt]{\ frac {dy}{d\varphi }}&=r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/341713e0b0d484e169fb6cc867ab6a6e31b7ca65)

![{\displaystyle L=\int _{a}^{b}{\sqrt {\left[r(\varphi )\right]^{2}+\left[{\tfrac {dr(\varphi )}{d\varphi }}\right]^{2}}}d\varphi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f62c06ac2868b9ac160abe1e75a075cad9e261)
![{\displaystyle {\frac {1}{2}}\int _{a}^{b}\left[r(\varphi )\right]^{2}\,d\varphi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fc7958a00360514f36fabcac7cab0361c2ae068)
![{\displaystyle \left[r(\varphi _{i})\right]^{2}\pi \cdot {\frac {\Delta \varphi }{2\pi }}={\frac {1}{2}}\left[r(\varphi _{i})\right]^{2}\Delta \varphi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec0cb32735f6a73076e1db62726c0eace3f000f6)

![{\displaystyle J=\det {\frac {\partial (x,y)}{\partial (r,\varphi )}}={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \varphi }}\\[2pt]{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \varphi }}\end{vmatrix}}={\begin{vmatrix}\cos \varphi &-r\sin \varphi \\\sin \varphi &r\cos \varphi \end{vmatrix}}=r\cos ^{2}\varphi +r\sin ^{2}\varphi =r.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52a1293fcb0e90b77017c0d9176c62aa06615b9b)











![{\displaystyle {\begin{aligned}\mathbf {r} &=(x,\ y)=r(\cos \varphi,\ \sin \varphi)=r {\hat {\mathbf {r} }}\ ,\\[1.5ex]{\dot {\mathbf {r} }}&=\left({\dot {x}},\ {\dot {y}}\right)={\dot {r}} (\cos \varphi ,\ \sin \varphi )+r{\dot {\varphi }}(-\sin \varphi ,\ \cos \varphi )={\dot {r}}{\hat {\mathbf { r} }}+r {\dot {\varphi }}{\hat {\boldsymbol {\varphi }}}\ ,\\[1.5ex]{\ddot {\mathbf {r} }}&=\left({\ddot {x}},\ {\ddot {y}}\right)\\[1ex]&={ \ddot {r}}(\cos \varphi ,\ \sin \varphi )+2{\dot {r}}{\dot {\varphi }}(-\sin \varphi ,\ \cos \varphi )+r {\ddot {\varphi }}(-\sin \varphi ,\ \cos \varphi )-r {\dot {\varphi }}^{2}(\cos \varphi ,\ \sin \varphi )\\[ 1ex]&=\left({\ddot {r}}-r{\dot {\varphi }}^{2}\right){\hat {\mathbf {r} }}+\left(r{\ddot {\varphi }}+2{\dot {r}}{\dot {\varphi }} \right){\hat {\boldsymbol {\varphi }}}\\[1ex]&=\left({\ddot {r}}-r{\dot {\varphi }}^{2}\right){ \hat {\mathbf {r} }}+{\frac {1}{r}}\;{\frac {d}{dt}}\left(r^{2}{\dot {\varphi }}\ вправо){\hat {\boldsymbol {\varphi }}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/272fcf3c718a928afd6ddced5527376aa6b5e58b)

![{\displaystyle {\begin{aligned}\mathbf {r} &=r(\theta){\hat {\mathbf {e} }}_{r}\\[1ex]{\frac {d\mathbf {r } {d\theta }}&={\frac {dr}{d\theta }}{\hat {\mathbf {e} }}_{r}+r{\hat {\mathbf {e} }} _{\theta }\\[1ex]{\frac {d^{2}\mathbf {r} {d\theta ^{2}}}&=\left({\frac {d^{2}r }{d\theta ^{2}}}-r\right){\hat {\mathbf {e} }}_{r}+{\frac {dr}{d\theta }}{\hat {\mathbf {e} }}_{\theta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e05ed720cc1c7b0eeb261f3941aade1fcec687a)




























