Дифференциальная геометрия
| Геометрия |
|---|
 |
| Геометры |
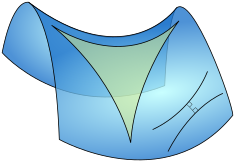
Дифференциальная геометрия — математическая дисциплина, изучающая геометрию гладких форм и гладких пространств, также известных как гладкие многообразия . Она использует методы дифференциального исчисления , интегрального исчисления , линейной алгебры и полилинейной алгебры . Область берет свое начало в изучении сферической геометрии еще в античности . Она также связана с астрономией , геодезией Земли и позднее с изучением гиперболической геометрии Лобачевским . Простейшими примерами гладких пространств являются плоские и пространственные кривые и поверхности в трехмерном евклидовом пространстве , и изучение этих форм легло в основу развития современной дифференциальной геометрии в XVIII и XIX веках.
С конца 19 века дифференциальная геометрия превратилась в область, занимающуюся в целом геометрическими структурами на дифференцируемых многообразиях . Геометрическая структура — это та, которая определяет некоторое понятие размера, расстояния, формы, объема или другой жесткой структуры. Например, в римановой геометрии указаны расстояния и углы, в симплектической геометрии могут быть вычислены объемы, в конформной геометрии указаны только углы, а в калибровочной теории заданы определенные поля над пространством. Дифференциальная геометрия тесно связана с дифференциальной топологией , которая занимается свойствами дифференцируемых многообразий, которые не полагаются на какую-либо дополнительную геометрическую структуру (см. эту статью для более подробного обсуждения различий между этими двумя предметами). Дифференциальная геометрия также связана с геометрическими аспектами теории дифференциальных уравнений , иначе известной как геометрический анализ .
Дифференциальная геометрия находит применение в математике и естественных науках . Наиболее заметно язык дифференциальной геометрии использовался Альбертом Эйнштейном в его общей теории относительности , а затем физиками при разработке квантовой теории поля и стандартной модели физики элементарных частиц . За пределами физики дифференциальная геометрия находит применение в химии , экономике , технике , теории управления , компьютерной графике и машинном зрении , а в последнее время и в машинном обучении .
История и развитие
История и развитие дифференциальной геометрии как предмета начинается, по крайней мере, еще в классической античности . Она тесно связана с развитием геометрии в целом, с понятием пространства и формы, а также с топологией , особенно с изучением многообразий . В этом разделе мы сосредоточимся в первую очередь на истории применения бесконечно малых методов к геометрии, а позднее на идеях касательных пространств и, в конечном итоге, на развитии современного формализма предмета в терминах тензоров и тензорных полей .
Классическая античность до эпохи Возрождения (300 г. до н.э. – 1600 г. н.э.)
Изучение дифференциальной геометрии или, по крайней мере, изучение геометрии гладких форм можно проследить, по крайней мере, до классической античности . В частности, многое было известно о геометрии Земли , сферической геометрии , во времена древнегреческих математиков . Известно, что Эратосфен вычислил окружность Земли около 200 г. до н. э., а около 150 г. н. э. Птолемей в своей «Географии» ввел стереографическую проекцию для целей картографирования формы Земли. [1] Неявно на протяжении всего этого времени принципы, которые составляют основу дифференциальной геометрии и исчисления, использовались в геодезии , хотя и в значительно упрощенной форме. А именно, еще в « Началах » Евклида понималось , что прямая линия может быть определена ее свойством обеспечивать кратчайшее расстояние между двумя точками, и применение этого же принципа к поверхности Земли приводит к выводу, что большие окружности , которые только локально подобны прямым линиям на плоскости, обеспечивают кратчайший путь между двумя точками на поверхности Земли. Действительно, измерения расстояний вдоль таких геодезических путей, проведенные Эратосфеном и другими, можно считать элементарной мерой длины дуги кривых, понятием, которое не имело строгого определения в терминах исчисления до 1600-х годов.
В это время существовало лишь минимальное открытое применение теории бесконечно малых к изучению геометрии, предшественника современного изучения предмета, основанного на исчислении. В « Началах » Евклида обсуждается понятие касания прямой к окружности, а Архимед применил метод исчерпывания для вычисления площадей гладких фигур, таких как круг , и объемов гладких трехмерных тел, таких как сфера, конусы и цилиндры. [1]
Теория дифференциальной геометрии мало развивалась между античностью и началом эпохи Возрождения . До разработки исчисления Ньютоном и Лейбницем наиболее значительное развитие в понимании дифференциальной геометрии произошло благодаря разработке Герардом Меркатором проекции Меркатора как способа картографирования Земли. Меркатор понимал преимущества и недостатки своего картографического дизайна и, в частности, осознавал конформную природу своей проекции, а также разницу между praga , линиями кратчайшего расстояния на Земле, и directio , прямыми линиями на своей карте. Меркатор отметил, что praga были косыми кривизнами в этой проекции. [1] Этот факт отражает отсутствие сохраняющей метрику карты земной поверхности на плоскость, что является следствием более поздней Theorema Egregium Гаусса .
После исчисления (1600–1800)

Первое систематическое или строгое рассмотрение геометрии с использованием теории бесконечно малых и понятий из исчисления началось около 1600-х годов, когда исчисление было впервые разработано Готфридом Лейбницем и Исааком Ньютоном . В это время недавняя работа Рене Декарта, вводящая аналитические координаты в геометрию, позволила строго описывать геометрические фигуры возрастающей сложности. В частности, примерно в это время Пьер де Ферма , Ньютон и Лейбниц начали изучать плоские кривые и исследовать такие понятия, как точки перегиба и окружности соприкосновения , которые помогают в измерении кривизны . Действительно, уже в своей первой статье об основах исчисления Лейбниц отмечает, что условие бесконечно малости указывает на существование точки перегиба. Вскоре после этого времени братья Бернулли , Якоб и Иоганн внесли важный ранний вклад в использование бесконечно малых для изучения геометрии. В лекциях Иоганна Бернулли того времени, позднее объединенных Лопиталем в первый учебник по дифференциальному исчислению , касательные к плоским кривым различных типов вычисляются с использованием условия , а также аналогичным образом вычисляются точки перегиба. [1] В это же время реализуется ортогональность между соприкасающимися окружностями плоской кривой и направлениями касательных, и записывается первая аналитическая формула для радиуса соприкасающейся окружности, по сути, первая аналитическая формула для понятия кривизны .
Вслед за развитием аналитической геометрии и плоских кривых Алексис Клеро начал изучать пространственные кривые всего в 16 лет. [2] [1] В своей книге Клеро ввел понятие касательных и субкасательных направлений к пространственным кривым относительно направлений, которые лежат вдоль поверхности , на которой лежит пространственная кривая. Таким образом, Клеро продемонстрировал неявное понимание касательного пространства поверхности и впервые изучил эту идею с помощью исчисления. Важно, что Клеро ввел терминологию кривизны и двойной кривизны , по сути, понятие главных кривизн, позже изученное Гауссом и другими.
Примерно в это же время Леонард Эйлер , первоначально ученик Иоганна Бернулли, внес значительный вклад не только в развитие геометрии, но и в математику в целом. [3] Что касается дифференциальной геометрии, Эйлер изучал понятие геодезической на поверхности, выводя первое аналитическое геодезическое уравнение , а позже ввел первый набор внутренних систем координат на поверхности, положив начало теории внутренней геометрии , на которой основаны современные геометрические идеи. [1] Примерно в это же время изучение Эйлером механики в «Механике» привело к осознанию того, что масса, движущаяся вдоль поверхности, не находящаяся под действием какой-либо силы, будет проходить по геодезической траектории, что стало ранним предшественником важных основополагающих идей общей теории относительности Эйнштейна , а также уравнений Эйлера–Лагранжа и первой теории вариационного исчисления , которая лежит в основе многих методов современной дифференциальной геометрии в симплектической геометрии и геометрическом анализе . Эта теория была использована Лагранжем , одним из разработчиков вариационного исчисления, для вывода первого дифференциального уравнения, описывающего минимальную поверхность в терминах уравнения Эйлера–Лагранжа. В 1760 году Эйлер доказал теорему, выражающую кривизну пространственной кривой на поверхности в терминах главных кривизн, известную как теорема Эйлера .
Позже, в 1700-х годах, новая французская школа под руководством Гаспара Монжа начала вносить вклад в дифференциальную геометрию. Монж внес важный вклад в теорию плоских кривых, поверхностей и изучал поверхности вращения и огибающие плоских кривых и пространственных кривых. Несколько учеников Монжа внесли вклад в эту же теорию, и, например, Шарль Дюпен дал новую интерпретацию теоремы Эйлера в терминах главных кривизн, что является современной формой уравнения. [1]
Внутренняя геометрия и неевклидова геометрия (1800–1900)
Дифференциальная геометрия стала самостоятельной областью изучения, отличной от более широкой идеи аналитической геометрии, в 1800-х годах, прежде всего благодаря основополагающим работам Карла Фридриха Гаусса и Бернхарда Римана , а также благодаря важному вкладу Николая Лобачевского в гиперболическую геометрию и неевклидову геометрию , а также в течение того же периода развития проективной геометрии .
Названный самой важной работой в истории дифференциальной геометрии, [4] в 1827 году Гаусс выпустил Disquisitiones generales circa superficies curvas, в котором подробно изложил общую теорию кривых поверхностей. [5] [4] [6] В этой работе и его последующих работах и неопубликованных заметках по теории поверхностей Гаусс был назван изобретателем неевклидовой геометрии и изобретателем внутренней дифференциальной геометрии. [6] В своей фундаментальной работе Гаусс ввел отображение Гаусса , гауссову кривизну , первую и вторую фундаментальные формы , доказал Theorema Egregium, показывающую внутреннюю природу гауссовой кривизны, и изучал геодезические, вычисляя площадь геодезического треугольника в различных неевклидовых геометриях на поверхностях.
В это время Гаусс уже придерживался мнения, что стандартная парадигма евклидовой геометрии должна быть отброшена, и обладал личными рукописями по неевклидовой геометрии, которые информировали его об изучении геодезических треугольников. [6] [7] Примерно в это же время Янош Бойяи и Лобачевский независимо друг от друга открыли гиперболическую геометрию и таким образом продемонстрировали существование последовательных геометрий за пределами парадигмы Евклида. Конкретные модели гиперболической геометрии были созданы Эугенио Бельтрами позже в 1860-х годах, а Феликс Клейн ввел термин неевклидова геометрия в 1871 году и посредством программы Эрланген поставил евклидову и неевклидову геометрии на одну основу. [8] Неявно, сферическая геометрия Земли, которая изучалась с античности, была неевклидовой геометрией, эллиптической геометрией .
Развитие внутренней дифференциальной геометрии на языке Гаусса было подстегнуто его учеником Бернхардом Риманом в его Habilitationsschrift , On the hypotheses that laid at the foundation of geometry . [9] В этой работе Риман впервые ввел понятие римановой метрики и тензора римановой кривизны и начал систематическое изучение дифференциальной геометрии в высших измерениях. Эта внутренняя точка зрения в терминах римановой метрики, обозначенная Риманом как , была развитием идеи Гаусса о линейном элементе поверхности. В это время Риман начал вводить систематическое использование линейной алгебры и полилинейной алгебры в предмет, широко используя теорию квадратичных форм в своем исследовании метрик и кривизны. В то время Риман еще не разработал современное понятие многообразия, поскольку даже понятие топологического пространства не встречалось, но он предположил, что можно было бы исследовать или измерить свойства метрики пространства-времени посредством анализа масс в пространстве-времени, связывая это с более ранним наблюдением Эйлера о том, что массы под действием никаких сил будут перемещаться по геодезическим линиям на поверхностях, и предсказал фундаментальное наблюдение Эйнштейна о принципе эквивалентности за целых 60 лет до того, как оно появилось в научной литературе. [6] [4]
Вслед за новым описанием Римана фокус методов, используемых для изучения дифференциальной геометрии, сместился с специальных и внешних методов изучения кривых и поверхностей на более систематический подход в терминах тензорного исчисления и программы Клейна Эрлангена, и прогресс в этой области увеличился. Понятие групп преобразований было разработано Софусом Ли и Жаном Гастоном Дарбу , что привело к важным результатам в теории групп Ли и симплектической геометрии . Понятие дифференциального исчисления на искривленных пространствах изучалось Элвином Кристоффелем , который ввел символы Кристоффеля , описывающие ковариантную производную в 1868 году, и другими, включая Эудженио Бельтрами , который изучал многие аналитические вопросы о многообразиях. [10] В 1899 году Луиджи Бьянки написал свои «Лекции по дифференциальной геометрии» , в которых изучал дифференциальную геометрию с точки зрения Римана, а год спустя Туллио Леви-Чивита и Грегорио Риччи-Курбастро выпустили свой учебник, систематически развивающий теорию абсолютного дифференциального исчисления и тензорного исчисления . [11] [4] Именно на этом языке дифференциальная геометрия использовалась Эйнштейном при разработке общей теории относительности и псевдоримановой геометрии .
Современная дифференциальная геометрия (1900–2000)
Предмет современной дифференциальной геометрии возник в начале 1900-х годов в ответ на основополагающие вклады многих математиков, включая, что важно, работу Анри Пуанкаре по основам топологии . [12] В начале 1900-х годов в математике возникло крупное движение по формализации основополагающих аспектов предмета, чтобы избежать кризисов строгости и точности, известное как программа Гильберта . В рамках этого более широкого движения понятие топологического пространства было выделено Феликсом Хаусдорфом в 1914 году, а к 1942 году существовало много различных понятий многообразия комбинаторной и дифференциально-геометрической природы. [12]
Интерес к предмету также был сфокусирован появлением общей теории относительности Эйнштейна и важностью уравнений поля Эйнштейна. Теория Эйнштейна популяризировала тензорное исчисление Риччи и Леви-Чивиты и ввела обозначения для римановой метрики и для символов Кристоффеля, оба из которых пришли из G в Гравитации . Эли Картан помог переформулировать основы дифференциальной геометрии гладких многообразий в терминах внешнего исчисления и теории подвижных систем отсчета , что привело в мире физики к теории Эйнштейна–Картана . [13] [4]
После этого раннего развития многие математики внесли свой вклад в развитие современной теории, включая Жана-Луи Кошуля , который ввел связности на векторных расслоениях , Шиинг-Шена Черна, который ввел характеристические классы в предмет и начал изучение комплексных многообразий , сэра Уильяма Валланса Дугласа Ходжа и Жоржа де Рама, которые расширили понимание дифференциальных форм , Чарльза Эресманна , который ввел теорию расслоений волокон и связностей Эресманна , и других. [13] [4] Особое значение имел Герман Вейль , который внес важный вклад в основы общей теории относительности, ввел тензор Вейля, обеспечивающий понимание конформной геометрии , и впервые определил понятие калибровки , что привело к развитию калибровочной теории в физике и математике .
В середине и конце 20-го века дифференциальная геометрия как предмет расширилась в своих границах и развила связи с другими областями математики и физики. Развитие калибровочной теории и теории Янга-Миллса в физике привлекло внимание к расслоениям и связям, что привело к развитию калибровочной теории . Было исследовано множество аналитических результатов, включая доказательство теоремы Атьи-Зингера об индексе . Развитие комплексной геометрии стимулировалось параллельными результатами в алгебраической геометрии , а результаты в геометрии и глобальном анализе комплексных многообразий были доказаны Шин-Тунгом Яу и другими. Во второй половине 20-го века были разработаны новые аналитические методы в отношении потоков кривизны, таких как поток Риччи , которые достигли кульминации в доказательстве Григорием Перельманом гипотезы Пуанкаре . В этот же период, в первую очередь благодаря влиянию Майкла Атьи , были сформированы новые связи между теоретической физикой и дифференциальной геометрией. Методы изучения уравнений Янга–Миллса и калибровочной теории использовались математиками для разработки новых инвариантов гладких многообразий. Такие физики, как Эдвард Виттен , единственный физик, удостоенный медали Филдса , оказали новое влияние на математику, используя топологическую квантовую теорию поля и теорию струн для предсказаний и предоставления рамок для новой строгой математики, что привело, например, к предполагаемой зеркальной симметрии и инвариантам Зайберга–Виттена .
Филиалы
Риманова геометрия
Риманова геометрия изучает римановы многообразия , гладкие многообразия с римановой метрикой . Это понятие расстояния, выраженное посредством гладкой положительно определенной симметричной билинейной формы, определенной на касательном пространстве в каждой точке. Риманова геометрия обобщает евклидову геометрию на пространства, которые не обязательно являются плоскими, хотя они все еще напоминают евклидово пространство в каждой точке бесконечно мало, т. е. в первом порядке приближения . Различные понятия, основанные на длине, такие как длина дуги кривых, площадь плоских областей и объем твердых тел, имеют естественные аналоги в римановой геометрии. Понятие производной по направлению функции из многомерного исчисления расширено до понятия ковариантной производной тензора . Многие понятия анализа и дифференциальных уравнений были обобщены на случай римановых многообразий .
Диффеоморфизм между римановыми многообразиями , сохраняющий расстояние, называется изометрией . Это понятие также может быть определено локально , т. е. для малых окрестностей точек. Любые две регулярные кривые локально изометричны. Однако теорема Egregium Карла Фридриха Гаусса показала, что для поверхностей существование локальной изометрии требует, чтобы гауссовы кривизны в соответствующих точках были одинаковыми. В более высоких размерностях тензор кривизны Римана является важным точечным инвариантом, связанным с римановым многообразием, который измеряет, насколько оно близко к плоскому. Важный класс римановых многообразий — римановы симметрические пространства , кривизна которых не обязательно постоянна. Это ближайшие аналоги «обычной» плоскости и пространства, рассматриваемых в евклидовой и неевклидовой геометрии .
Псевдориманова геометрия
Псевдориманова геометрия обобщает риманову геометрию на случай, когда метрический тензор не обязательно должен быть положительно-определенным . Частным случаем этого является лоренцево многообразие , которое является математической основой общей теории относительности Эйнштейна .
Геометрия Финслера
Финслерова геометрия имеет финслеровы многообразия в качестве основного объекта изучения. Это дифференциальное многообразие с финслеровой метрикой , то есть банаховой нормой , определенной на каждом касательном пространстве. Римановы многообразия являются частными случаями более общих финслеровых многообразий. Финслерова структура на многообразии — это функция такая, что:
- для всех и всего ,
- бесконечно дифференцируема по ,
- Вертикальный гессиан положительно определен.
Симплектическая геометрия
Симплектическая геометрия — это изучение симплектических многообразий . Почти симплектическое многообразие — это дифференцируемое многообразие, снабженное плавно меняющейся невырожденной кососимметричной билинейной формой на каждом касательном пространстве, т. е. невырожденной 2- формой ω , называемой симплектической формой . Симплектическое многообразие — это почти симплектическое многообразие, для которого симплектическая форма ω замкнута: d ω = 0 .
Диффеоморфизм между двумя симплектическими многообразиями, сохраняющий симплектическую форму, называется симплектоморфизмом . Невырожденные кососимметричные билинейные формы могут существовать только на четномерных векторных пространствах, поэтому симплектические многообразия обязательно имеют четную размерность. В размерности 2 симплектическое многообразие — это просто поверхность, наделенная формой площади, а симплектоморфизм — это диффеоморфизм, сохраняющий площадь. Фазовое пространство механической системы — это симплектическое многообразие, и они неявно появились уже в работах Жозефа Луи Лагранжа по аналитической механике , а позднее в формулировках классической механики Карла Густава Якоби и Уильяма Роуэна Гамильтона .
В отличие от римановой геометрии, где кривизна обеспечивает локальный инвариант римановых многообразий, теорема Дарбу утверждает, что все симплектические многообразия локально изоморфны. Единственные инварианты симплектического многообразия являются глобальными по своей природе, и топологические аспекты играют важную роль в симплектической геометрии. Первым результатом в симплектической топологии, вероятно, является теорема Пуанкаре–Биркгофа , выдвинутая Анри Пуанкаре и затем доказанная Дж. Д. Биркгофом в 1912 году. Она утверждает, что если сохраняющее площадь отображение кольца скручивает каждую граничную компоненту в противоположных направлениях, то отображение имеет по крайней мере две неподвижные точки. [14]
Геометрия контакта
Контактная геометрия имеет дело с некоторыми многообразиями нечетной размерности. Она близка к симплектической геометрии и, как и последняя, возникла в вопросах классической механики. Контактная структура на (2 n + 1) -мерном многообразии M задается гладким гиперплоскостным полем H в касательном расслоении , которое максимально далеко от того, чтобы быть связанным с уровнями дифференцируемой функции на M (технический термин — «полностью неинтегрируемое распределение касательной гиперплоскости»). Вблизи каждой точки p гиперплоскостное распределение определяется нигде не исчезающей 1-формой , которая единственна с точностью до умножения на нигде не исчезающую функцию:
Локальная 1-форма на M является контактной формой , если ограничение ее внешней производной на H является невырожденной 2-формой и, таким образом, индуцирует симплектическую структуру на H p в каждой точке. Если распределение H может быть определено глобальной 1-формой , то эта форма является контактной тогда и только тогда, когда форма высшей размерности
является формой объема на M , т. е. нигде не обращается в нуль. Имеет место контактный аналог теоремы Дарбу: все контактные структуры на нечетномерном многообразии локально изоморфны и могут быть приведены к некоторой локальной нормальной форме с помощью подходящего выбора системы координат.
Комплексная и кэлерова геометрия
Комплексная дифференциальная геометрия изучает комплексные многообразия . Почти комплексное многообразие — это вещественное многообразие , наделенное тензором типа (1, 1), т.е. эндоморфизмом векторного расслоения (называемым почти комплексной структурой ).
- , такой что
Из этого определения следует, что почти комплексное многообразие является четномерным.
Почти комплексное многообразие называется комплексным , если , где — тензор типа (2, 1), связанный с , называемый тензором Нийенхейса (или иногда кручением ). Почти комплексное многообразие является комплексным тогда и только тогда, когда оно допускает голоморфный координатный атлас . Почти эрмитова структура задается почти комплексной структурой J , вместе с римановой метрикой g , удовлетворяющей условию совместимости
Почти эрмитова структура естественным образом определяет дифференциальную двумерную форму
Следующие два условия эквивалентны:
где — связность Леви-Чивита для . В этом случае называется кэлеровой структурой , а кэлерово многообразие — это многообразие, наделенное кэлеровой структурой. В частности, кэлерово многообразие является как комплексным, так и симплектическим многообразием . Большой класс кэлеровых многообразий (класс многообразий Ходжа ) задается всеми гладкими комплексными проективными многообразиями .
Геометрия CR
Геометрия CR изучает внутреннюю геометрию границ областей в комплексных многообразиях .
Конформная геометрия
Конформная геометрия — это изучение множества сохраняющих угол (конформных) преобразований пространства.
Дифференциальная топология
Дифференциальная топология — это изучение глобальных геометрических инвариантов без метрической или симплектической формы.
Дифференциальная топология начинается с естественных операций, таких как производная Ли натуральных векторных расслоений и дифференциал де Рама форм . Помимо алгеброидов Ли , также алгеброиды Куранта начинают играть более важную роль.
Группы Ли
Группа Ли — это группа в категории гладких многообразий. Помимо алгебраических свойств она обладает также дифференциально-геометрическими свойствами. Наиболее очевидной конструкцией является конструкция алгебры Ли, которая является касательным пространством в единице, снабженной скобкой Ли между левоинвариантными векторными полями . Помимо теории структур существует также широкая область теории представлений .
Геометрический анализ
Геометрический анализ — это математическая дисциплина, в которой инструменты дифференциальных уравнений, особенно эллиптических уравнений в частных производных, используются для установления новых результатов в дифференциальной геометрии и дифференциальной топологии.
Калибровочная теория
Калибровочная теория — это изучение связей на векторных расслоениях и главных расслоениях, и возникает из проблем математической физики и физических калибровочных теорий , которые лежат в основе стандартной модели физики элементарных частиц . Калибровочная теория занимается изучением дифференциальных уравнений для связей на расслоениях и результирующих геометрических модульных пространств решений этих уравнений, а также инвариантов, которые могут быть выведены из них. Эти уравнения часто возникают как уравнения Эйлера–Лагранжа, описывающие уравнения движения определенных физических систем в квантовой теории поля , и поэтому их изучение представляет значительный интерес в физике.
Связки и соединения
Аппарат векторных расслоений , главных расслоений и связностей на расслоениях играет чрезвычайно важную роль в современной дифференциальной геометрии. Гладкое многообразие всегда несет естественное векторное расслоение, касательное расслоение . Грубо говоря, эта структура сама по себе достаточна только для разработки анализа на многообразии, в то время как для выполнения геометрии требуется, кроме того, некоторый способ связать касательные пространства в разных точках, т. е. понятие параллельного переноса . Важный пример дают аффинные связности . Для поверхности в R 3 касательные плоскости в разных точках могут быть идентифицированы с помощью естественного параллельного пути, индуцированного окружающим евклидовым пространством, которое имеет хорошо известное стандартное определение метрики и параллельности. В римановой геометрии связность Леви-Чивиты служит аналогичной цели. В более общем смысле, дифференциальные геометры рассматривают пространства с векторным расслоением и произвольной аффинной связностью, которая не определяется в терминах метрики. В физике многообразие может быть пространством-временем , а расслоения и связности связаны с различными физическими полями.
Внутреннее против внешнего
С начала и до середины XIX века дифференциальная геометрия изучалась с внешней точки зрения: кривые и поверхности рассматривались как лежащие в евклидовом пространстве более высокой размерности (например, поверхность в окружающем пространстве трех измерений). Простейшие результаты получены в дифференциальной геометрии кривых и дифференциальной геометрии поверхностей. Начиная с работ Римана , была разработана внутренняя точка зрения, в которой нельзя говорить о движении «вне» геометрического объекта, поскольку он считается данным в свободном виде. Основным результатом здесь является теорема Гаусса egregium о том, что гауссова кривизна является внутренним инвариантом.
Внутренняя точка зрения более гибкая. Например, она полезна в теории относительности, где пространство-время не может быть естественным образом принято как внешнее. Однако за это приходится платить технической сложностью: внутренние определения кривизны и связей становятся гораздо менее визуально интуитивными.
Эти две точки зрения можно примирить, т.е. внешнюю геометрию можно рассматривать как структуру, дополнительную к внутренней. (См. теорему вложения Нэша .) В формализме геометрического исчисления как внешняя, так и внутренняя геометрия многообразия может быть охарактеризована одной бивекторнозначной одноформой, называемой оператором формы . [15]
Приложения
| Part of a series on |
| Spacetime |
|---|
 |
Ниже приведены некоторые примеры применения дифференциальной геометрии в других областях науки и математики.
- В физике дифференциальная геометрия имеет множество приложений, в том числе:
- Дифференциальная геометрия — это язык, на котором выражена общая теория относительности Альберта Эйнштейна . Согласно этой теории, Вселенная представляет собой гладкое многообразие, снабженное псевдоримановой метрикой, которая описывает кривизну пространства-времени . Понимание этой кривизны необходимо для позиционирования спутников на орбите вокруг Земли. Дифференциальная геометрия также незаменима при изучении гравитационного линзирования и черных дыр .
- Дифференциальные формы используются при изучении электромагнетизма .
- Дифференциальная геометрия имеет приложения как к лагранжевой механике , так и к гамильтоновой механике . Симплектические многообразия в частности могут быть использованы для изучения гамильтоновых систем .
- Риманова геометрия и контактная геометрия были использованы для построения формализма геометротермодинамики , который нашел применение в классической равновесной термодинамике .
- В химии и биофизике при моделировании структуры клеточной мембраны под действием переменного давления.
- В экономике дифференциальная геометрия имеет приложения в области эконометрики . [16]
- Геометрическое моделирование (включая компьютерную графику ) и компьютерное геометрическое проектирование опираются на идеи дифференциальной геометрии.
- В инженерии дифференциальная геометрия может применяться для решения задач цифровой обработки сигналов . [17]
- В теории управления дифференциальная геометрия может использоваться для анализа нелинейных регуляторов, в частности геометрического управления [18]
- В теории вероятности , статистике и теории информации можно интерпретировать различные структуры как римановы многообразия, что дает область информационной геометрии , в частности, с помощью информационной метрики Фишера .
- В структурной геологии дифференциальная геометрия используется для анализа и описания геологических структур.
- В компьютерном зрении дифференциальная геометрия используется для анализа форм. [19]
- В обработке изображений дифференциальная геометрия используется для обработки и анализа данных на неплоских поверхностях. [20]
- Доказательство Григория Перельмана гипотезы Пуанкаре с использованием техники потоков Риччи продемонстрировало мощь дифференциально-геометрического подхода к вопросам топологии и подчеркнуло важную роль, которую играют его аналитические методы.
- В беспроводной связи грассмановы многообразия используются для методов формирования луча в многоантенных системах. [21]
- В геодезии — для вычисления расстояний и углов на поверхности среднего уровня моря Земли , моделируемой эллипсоидом вращения.
Смотрите также
- Аффинная дифференциальная геометрия
- Анализ фракталов
- Базовое введение в математику искривленного пространства-времени
- Дискретная дифференциальная геометрия
- Гаусс
- Глоссарий дифференциальной геометрии и топологии
- Важные публикации по дифференциальной геометрии
- Важные публикации по дифференциальной топологии
- Интегральная геометрия
- Список тем по дифференциальной геометрии
- Некоммутативная геометрия
- Проективно-дифференциальная геометрия
- Синтетическая дифференциальная геометрия
- Систолическая геометрия
- Калибровочная теория (математика)
Ссылки
- ^ abcdefg Struik, DJ «Очерк истории дифференциальной геометрии: I». Isis, т. 19, № 1, 1933, стр. 92–120. JSTOR, www.jstor.org/stable/225188.
- ^ Клеро, AC, 1731. Recherches sur les Courbes à Double Courbere. Ньон.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Леонард Эйлер», Архив истории математики Мактьютора , Университет Сент-Эндрюс
- ^ abcdef Спивак, М., 1975. Всеобъемлющее введение в дифференциальную геометрию (т. 2). Publish or Perish, Incorporated.
- ^ Гаусс, CF, 1828. Disquisitiones Generales circa superficies Curvas (Том 1). Типис Дитерихианис.
- ^ abcd Struik, DJ "Очерк истории дифференциальной геометрии (II)". Isis, т. 20, № 1, 1933, стр. 161–191. JSTOR, www.jstor.org/stable/224886
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Неевклидова геометрия», Архив истории математики Мактьютора , Университет Сент-Эндрюс
- ^ Милнор, Джон У. , (1982) Гиперболическая геометрия: первые 150 лет , Bull. Amer. Math. Soc. (NS) Том 6, Номер 1, стр. 9–24.
- ^ 1868 О гипотезах, лежащих в основе геометрии , перевод WKClifford , Nature 8 1873 183 – перепечатано в Clifford's Collected Mathematical Papers, London 1882 (MacMillan); New York 1968 (Chelsea) http://www.emis.de/classics/Riemann/. Также в Ewald, William B., ed., 1996 "From Kant to Hilbert: A Source Book in the Foundations of Mathematics", 2 vols. Oxford Uni. Press: 652–61.
- ^ Кристоффель, Э.Б. (1869). «Ueber die Transformation der homogenen Differentialausdrücke zweiten Grades». Журнал для королевы и математики . 70 .
- ^ Риччи, Грегорио; Леви-Чивита, Туллио (март 1900 г.). «Методы абсолютного дифференциального исчисления и их приложения». Mathematische Annalen (на французском языке). 54 (1–2). Спрингер: 125–201. дои : 10.1007/BF01454201. S2CID 120009332.
- ^ ab Dieudonné, J., 2009. История алгебраической и дифференциальной топологии, 1900-1960. Springer Science & Business Media.
- ^ ab Fré, PG, 2018. Концептуальная история пространства и симметрии. Springer, Cham.
- ^ Условие сохранения площади (или условие скручивания) не может быть удалено. Если попытаться распространить такую теорему на более высокие размерности, то, вероятно, можно предположить, что сохраняющее объем отображение определенного типа должно иметь неподвижные точки. Это неверно в размерностях больше 3.
- ^ Хестенес, Дэвид (2011). «Форма дифференциальной геометрии в геометрическом исчислении» (PDF) . В Дорст, Л.; Ласенби, Дж. (ред.). Руководство по геометрической алгебре на практике . Springer Verlag. стр. 393–410.
- ^ Marriott, Paul; Salmon, Mark, ред. (2000). Applications of Differential Geometry to Econometrics . Cambridge University Press. ISBN 978-0-521-65116-5.
- ^ Manton, Jonathan H. (2005). "О роли дифференциальной геометрии в обработке сигналов". Труды. (ICASSP '05). Международная конференция IEEE по акустике, речи и обработке сигналов, 2005. Том 5. стр. 1021–1024. doi :10.1109/ICASSP.2005.1416480. ISBN 978-0-7803-8874-1. S2CID 12265584.
- ^ Булло, Франческо; Льюис, Эндрю (2010). Геометрическое управление механическими системами: моделирование, анализ и проектирование простых механических систем управления . Springer-Verlag. ISBN 978-1-4419-1968-7.
- ^ Микели, Марио (май 2008 г.). Дифференциальная геометрия многообразий знаковых фигур: метрики, геодезические и кривизна (PDF) (Ph.D.). Архивировано из оригинала (PDF) 4 июня 2011 г.
- ^ Джоши, Ананд А. (август 2008 г.). Геометрические методы обработки изображений и анализа сигналов (PDF) (Ph.D.). Архивировано (PDF) из оригинала 2011-07-20.
- ^ Love, David J.; Heath, Robert W. Jr. (октябрь 2003 г.). «Grassmannian Beamforming for Multiple-Input Multiple-Output Wireless Systems» (PDF) . IEEE Transactions on Information Theory . 49 (10): 2735–2747. CiteSeerX 10.1.1.106.4187 . doi :10.1109/TIT.2003.817466. Архивировано из оригинала (PDF) 2008-10-02.
Дальнейшее чтение
- Этан Д. Блох (27 июня 2011 г.). Первый курс геометрической топологии и дифференциальной геометрии. Бостон: Springer Science & Business Media. ISBN 978-0-8176-8122-7. OCLC 811474509.
- Берк, Уильям Л. (1997). Прикладная дифференциальная геометрия. Cambridge University Press. ISBN 0-521-26929-6. OCLC 53249854.
- ду Карму, Манфреду Пердигау (1976). Дифференциальная геометрия кривых и поверхностей. Энглвуд Клиффс, Нью-Джерси: Prentice-Hall. ISBN 978-0-13-212589-5. OCLC 1529515.
- Франкель, Теодор (2004). Геометрия физики: введение (2-е изд.). Нью-Йорк: Cambridge University Press. ISBN 978-0-521-53927-2. OCLC 51855212.
- Эльза Аббена; Саймон Саламон; Альфред Грей (2017). Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica (3-е изд.). Бока-Ратон: Chapman and Hall/CRC. ISBN 978-1-351-99220-6. OCLC 1048919510.
- Крейсциг, Эрвин (1991). Дифференциальная геометрия. Нью-Йорк: Dover Publications. ISBN 978-0-486-66721-8. OCLC 23384584.
- Кюнель, Вольфганг (2002). Дифференциальная геометрия: кривые – поверхности – многообразия (2-е изд.). Провиденс, Род-Айленд: Американское математическое общество. ISBN 978-0-8218-3988-1. OCLC 61500086.
- Макклири, Джон (1994). Геометрия с дифференцируемой точки зрения. Cambridge University Press. ISBN 0-521-13311-4. OCLC 915912917.
- Спивак, Майкл (1999). Всеобъемлющее введение в дифференциальную геометрию (5 томов) (3-е изд.). Опубликуй или погибни. ISBN 0-914098-72-1. OCLC 179192286.
- ter Haar Romeny, Bart M. (2003). Front-end vision и multi-scale image analysis: multi-scale computer vision theory and applications, написанная в Mathematica. Дордрехт: Kluwer Academic. ISBN 978-1-4020-1507-6. OCLC 52806205.
Внешние ссылки
- «Дифференциальная геометрия», Энциклопедия математики , EMS Press , 2001 [1994]
- Б. Конрад. Раздаточные материалы по дифференциальной геометрии, Стэнфордский университет
- Онлайн-курс дифференциальной геометрии Майкла Мюррея, 1996 г. Архивировано 01.08.2013 на Wayback Machine
- Современный курс по кривым и поверхностям, Ричард С. Пале, 2003 г. Архивировано 09.04.2019 в Wayback Machine
- Галерея 3DXM-поверхностей Ричарда Пале, архив 2019-04-09 на Wayback Machine
- Заметки Балаша Чикоша по дифференциальной геометрии, заархивированные 5 июня 2009 г. в Wayback Machine.
- Н. Дж. Хикс, Заметки о дифференциальной геометрии, Ван Ностранд.
- MIT OpenCourseWare: Дифференциальная геометрия, осень 2008 г.