Первообразный

Неопределенный интеграл

{\displaystyle F(x)={\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}-x+c} — Поле наклона , показывающее три из бесконечного множества решений, которые можно получить, изменяя произвольную константу $c$ . $F(x)={\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}-x+c$

В исчислении первообразная , обратная производная , примитивная функция , примитивный интеграл или неопределенный интеграл ^{[Примечание 1]} непрерывной функции $f$ — это дифференцируемая функция $F,$ производная которой равна исходной функции $f$ . Это можно символически записать как $F' = f$ . ^[1]^[2] Процесс решения для первообразных называется антидифференцированием (или неопределенным интегрированием ), а его обратная операция называется дифференцированием , то есть процессом нахождения производной. Первообразные часто обозначаются заглавными латинскими буквами, такими как $F$ и $G.$

Первообразные связаны с определенными интегралами посредством второй основной теоремы исчисления : определенный интеграл функции на замкнутом интервале , где функция интегрируема по Риману, равен разности между значениями первообразной, вычисленными в конечных точках интервала.

В физике первообразные возникают в контексте прямолинейного движения (например, при объяснении связи между положением , скоростью и ускорением ). ^[3]Дискретным эквивалентом понятия первообразной является антиразность .

Примеры

Функция является первообразной , так как производная от равна . Так как производная константы равна нулю , будет иметь бесконечное число первообразных, таких как , и т.д. Таким образом, все первообразные от могут быть получены путем изменения значения $c$ в , где $c$ — произвольная константа, известная как константа интегрирования . Графики первообразных заданной функции являются вертикальными переносами друг друга, причем вертикальное положение каждого графика зависит от значения $c$ . $F(x)={\tfrac {x^{3}}{3}}$ $f(x)=x^{2}$ ${\tfrac {x^{3}}{3}}$ $x^{2}$ $x^{2}$ ${\tfrac {x^{3}}{3}},{\tfrac {x^{3}}{3}}+1,{\tfrac {x^{3}}{3}}-2$ $x^{2}$ $F(x)={\tfrac {x^{3}}{3}}+c$

В более общем случае степенная функция имеет первообразную , если $n$ $\neq -1$ и если $n$ $= -1$ . $f(x)=x^{n}$ $F(x)={\tfrac {x^{n+1}}{n+1}}+c$ $F(x)=\ln |x|+c$

В физике интегрирование ускорения дает скорость плюс константу. Константа — это начальный член скорости, который будет потерян при вычислении производной скорости, поскольку производная постоянного члена равна нулю. Эта же закономерность применима к дальнейшим интегрированиям и производным движения (положение, скорость, ускорение и т. д.). ^[3] Таким образом, интегрирование дает соотношения ускорения, скорости и смещения : ${\begin{aligned}\int a\,\mathrm {d} t&=v+C\\\int v\,\mathrm {d} t&=s+C\end{aligned}}$

Использование и свойства

Первообразные можно использовать для вычисления определенных интегралов , используя основную теорему исчисления : если $F$ является первообразной непрерывной функции $f$ на интервале , то: $[a,b]$ $\int _{a}^{b}f(x)\,\mathrm {d} x=F(b)-F(a).$

По этой причине каждую из бесконечного множества первообразных данной функции $f$ можно назвать «неопределенным интегралом» функции f и записать с использованием символа интеграла без ограничений: $\int f(x)\,\mathrm {d} x.$

Если $F$ является первообразной функции $f$ , и функция $f$ определена на некотором интервале, то любая другая первообразная $G$ функции $f$ отличается от $F$ константой: существует число $c$ такое, что для всех $x$ . $c$ называется константой интегрирования . Если область определения $F$ является несвязным объединением двух или более (открытых) интервалов, то для каждого из интервалов может быть выбрана своя константа интегрирования. Например, $G(x)=F(x)+c$ $F(x)={\begin{cases}-{\dfrac {1}{x}}+c_{1}&x<0\\[1ex]-{\dfrac {1}{x}}+c_{2}&x>0\end{cases}}$

является наиболее общей первообразной в ее естественной области определения $f(x)=1/x^{2}$ $(-\infty ,0)\cup (0,\infty ).$

Каждая непрерывная функция $f$ имеет первообразную, и одна первообразная $F$ задается определенным интегралом $f$ с переменной верхней границей: для любого $a$ в области определения $f$ . Изменение нижней границы дает другие первообразные, но не обязательно все возможные первообразные. Это еще одна формулировка основной теоремы исчисления . $F(x)=\int _{a}^{x}f(t)\,\mathrm {d} t~,$

Существует много элементарных функций , чьи первообразные, хотя они и существуют, не могут быть выражены через элементарные функции. Элементарными функциями являются полиномы , показательные функции , логарифмы , тригонометрические функции , обратные тригонометрические функции и их комбинации по композиции и линейной комбинации . Примерами этих неэлементарных интегралов являются

функция ошибки $\int e^{-x^{2}}\,\mathrm {d} x,$
функция Френеля $\int \sin x^{2}\,\mathrm {d} x,$
интегральный синус $\int {\frac {\sin x}{x}}\,\mathrm {d} x,$
логарифмическая интегральная функция и $\int {\frac {1}{\log x}}\,\mathrm {d} x,$
мечта второкурсника $\int x^{x}\,\mathrm {d} x.$

Более подробное обсуждение см. также в разделе Дифференциальная теория Галуа .

Методы интеграции

Нахождение первообразных элементарных функций часто значительно сложнее, чем нахождение их производных (действительно, не существует предопределенного метода вычисления неопределенных интегралов). ^[4] Для некоторых элементарных функций невозможно найти первообразную в терминах других элементарных функций. Чтобы узнать больше, см. элементарные функции и неэлементарный интеграл .

Существует множество свойств и методов поиска первообразных. К ним относятся, среди прочего:

Линейность интегрирования (которая разбивает сложные интегралы на более простые)
Интеграция путем подстановки , часто в сочетании с тригонометрическими тождествами или натуральным логарифмом
Метод обратного цепного правила (частный случай интегрирования путем подстановки)
Интеграция по частям (интегрировать произведения функций)
Интегрирование обратной функции (формула, выражающая первообразную обратной функции $f -1$ обратимой и непрерывной функции $f$ через $f -1$ и первообразную $f$ ).
Метод простейших дробей в интегрировании (позволяющий интегрировать все рациональные функции — дроби двух многочленов)
Алгоритм Риша
Дополнительные методы для многократного интегрирования (см., например, двойные интегралы , полярные координаты , якобиан и теорему Стокса )
Численное интегрирование (метод приближения определенного интеграла, когда не существует элементарной первообразной, как в случае $exp(- x 2)$ )
Алгебраическая манипуляция подынтегральным выражением (чтобы можно было использовать другие методы интегрирования, такие как интегрирование путем подстановки)
Формула Коши для повторного интегрирования (для вычисления $n$ -кратной первообразной функции) $\int _{x_{0}}^{x}\int _{x_{0}}^{x_{1}}\cdots \int _{x_{0}}^{x_{n-1}}f(x_{n})\,\mathrm {d} x_{n}\cdots \,\mathrm {d} x_{2}\,\mathrm {d} x_{1}=\int _{x_{0}}^{x}f(t){\frac {(x-t)^{n-1}}{(n-1)!}}\,\mathrm {d} t.$

Системы компьютерной алгебры могут использоваться для автоматизации части или всей работы, связанной с символическими методами, описанными выше, что особенно полезно, когда задействованные алгебраические манипуляции очень сложны или длинны. Интегралы, которые уже были выведены, можно найти в таблице интегралов .

Ненепрерывных функций

Ненепрерывные функции могут иметь первообразные. Хотя в этой области все еще есть открытые вопросы, известно, что:

Некоторые высокопатологические функции с большими наборами разрывов могут, тем не менее, иметь первообразные.
В некоторых случаях первообразные таких патологических функций могут быть найдены путем интегрирования по Риману , в то время как в других случаях эти функции не интегрируются по Риману.

Предполагая, что области определения функций представляют собой открытые интервалы:

Необходимым, но не достаточным условием для того, чтобы функция $f$ имела первообразную, является наличие у $f$ свойства промежуточного значения . То есть, если $[a, b]$ — подынтервал области определения $f$ , а $y$ — любое действительное число между $f (a)$ и $f (b)$ , то существует $c$ между $a$ и $b,$ такое что $f (c) = y$ . Это следствие теоремы Дарбу .
Множество разрывов функции $f$ должно быть разреженным множеством . Это множество также должно быть множеством F-сигма (поскольку множество разрывов любой функции должно быть этого типа). Более того, для любого разреженного множества F-сигма можно построить некоторую функцию $f,$ имеющую первообразную, которая имеет заданное множество в качестве своего множества разрывов.
Если $f$ имеет первообразную, ограничена на замкнутых конечных подынтервалах области и имеет множество разрывов меры Лебега 0, то первообразная может быть найдена путем интегрирования в смысле Лебега. Фактически, используя более мощные интегралы, такие как интеграл Хенстока–Курцвейля , каждая функция, для которой существует первообразная, интегрируема, и ее общий интеграл совпадает с ее первообразной.
Если $f$ имеет первообразную $F$ на замкнутом интервале , то для любого выбора разбиения , если выбрать точки выборки , как указано в теореме о среднем значении , то соответствующая сумма Римана сжимается до значения . Однако, если $f$ неограничена или если $f$ ограничена, но множество разрывов $f$ имеет положительную меру Лебега, другой выбор точек выборки может дать существенно другое значение для суммы Римана, независимо от того, насколько мелко разбиение. См. пример 4 ниже. $[a,b]$ $a=x_{0}<x_{1}<x_{2}<\dots <x_{n}=b,$ $x_{i}^{*}\in [x_{i-1},x_{i}]$ $F(b)-F(a)$ ${\begin{aligned}\sum _{i=1}^{n}f(x_{i}^{*})(x_{i}-x_{i-1})&=\sum _{i=1}^{n}[F(x_{i})-F(x_{i-1})]\\&=F(x_{n})-F(x_{0})=F(b)-F(a)\end{aligned}}$ $x_{i}^{*}$

Некоторые примеры

Функция
$f(x)=2x\sin \left({\frac {1}{x}}\right)-\cos \left({\frac {1}{x}}\right)$ с не является непрерывным при , но имеет первообразную $f(0)=0$ $x=0$ $F(x)=x^{2}\sin \left({\frac {1}{x}}\right)$
с . Поскольку $f$ ограничена на замкнутых конечных интервалах и разрывна только в точке 0, первообразная $F$ может быть получена путем интегрирования: . $F(0)=0$ $F(x)=\int _{0}^{x}f(t)\,\mathrm {d} t$
Функция при не является непрерывной при , но имеет первообразную при . В отличие от примера 1, $f$ $($ $x$ $)$ не ограничена в любом интервале, содержащем 0, поэтому интеграл Римана не определен. $f(x)=2x\sin \left({\frac {1}{x^{2}}}\right)-{\frac {2}{x}}\cos \left({\frac {1}{x^{2}}}\right)$ $f(0)=0$ $x=0$ $F(x)=x^{2}\sin \left({\frac {1}{x^{2}}}\right)$ $F(0)=0$
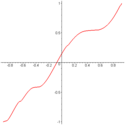
Если $f (x)$ — функция из примера 1, а $F$ — ее первообразная, и является плотным счетным подмножеством открытого интервала , то функция имеет первообразную Множество разрывов функции $g$ — это в точности множество . Поскольку $функция g$ ограничена на замкнутых конечных интервалах, а множество разрывов имеет меру 0, первообразная $G$ может быть найдена путем интегрирования. $\{x_{n}\}_{n\geq 1}$ $(-1,1),$ $g(x)=\sum _{n=1}^{\infty }{\frac {f(x-x_{n})}{2^{n}}}$ $G(x)=\sum _{n=1}^{\infty }{\frac {F(x-x_{n})}{2^{n}}}.$ $\{x_{n}\}_{n\geq 1}$
Пусть — плотное счетное подмножество открытого интервала. Рассмотрим всюду непрерывную строго возрастающую функцию. Можно показать, что $\{x_{n}\}_{n\geq 1}$ $(-1,1).$ $F(x)=\sum _{n=1}^{\infty }{\frac {1}{2^{n}}}(x-x_{n})^{1/3}.$ $F'(x)=\sum _{n=1}^{\infty }{\frac {1}{3\cdot 2^{n}}}(x-x_{n})^{-2/3}$
Рисунок 1.
Рисунок 2.
для всех значений $x$ , где ряд сходится, и что график $F (x)$ имеет вертикальные касательные линии при всех других значениях $x$ . В частности, график имеет вертикальные касательные линии во всех точках множества . $\{x_{n}\}_{n\geq 1}$
Более того , для всех $x$ , где определена производная. Отсюда следует, что обратная функция дифференцируема всюду и что $F(x)\geq 0$ $G=F^{-1}$ $g(x)=G'(x)=0$
для всех $x$ в множестве , которое плотно в интервале Таким образом, $g$ имеет первообразную $G.$ С другой стороны, не может быть верным, что $\{F(x_{n})\}_{n\geq 1}$ $[F(-1),F(1)].$ $\int _{F(-1)}^{F(1)}g(x)\,\mathrm {d} x=GF(1)-GF(-1)=2,$
так как для любого разбиения , можно выбрать точки выборки для суммы Римана из множества , задавая значение 0 для суммы. Отсюда следует, что $g$ имеет множество разрывов положительной меры Лебега. На рисунке 1 справа показано приближение к графику $g$ $($ $x$ $)$ , где и ряд усечен до 8 членов. На рисунке 2 показан график приближения к первообразной $G$ $($ $x$ $)$ , также усеченной до 8 членов. С другой стороны, если интеграл Римана заменить интегралом Лебега , то лемма Фату или теорема о доминируемой сходимости показывают, что $g$ удовлетворяет основной теореме исчисления в этом контексте. $[F(-1),F(1)]$ $\{F(x_{n})\}_{n\geq 1}$ $\{x_{n}=\cos(n)\}_{n\geq 1}$
В примерах 3 и 4 множества разрывов функций $g$ плотны только на конечном открытом интервале Однако эти примеры можно легко модифицировать так, чтобы иметь множества разрывов, плотные на всей действительной прямой . Пусть Тогда имеет плотное множество разрывов на и имеет первообразную $(a,b).$ $(-\infty ,\infty )$ $\lambda (x)={\frac {a+b}{2}}+{\frac {b-a}{\pi }}\tan ^{-1}x.$ $g(\lambda (x))\lambda '(x)$ $(-\infty ,\infty )$ $G\cdot \lambda .$
Используя метод, аналогичный методу в примере 5, можно изменить $g$ в примере 4 так, чтобы он обращался в нуль при всех рациональных числах . Если использовать наивную версию интеграла Римана, определяемую как предел левых или правых сумм Римана по регулярным разбиениям, то получится, что интеграл такой функции $g$ по интервалу равен 0, когда $a$ и $b$ оба рациональны, вместо . Таким образом, фундаментальная теорема исчисления будет полностью нарушена. $[a,b]$ $G(b)-G(a)$
Функция, имеющая первообразную, может все еще не быть интегрируемой по Риману. Примером может служить производная функции Вольтерра .

Основные формулы

Если , то . ${\mathrm {d} \over \mathrm {d} x}f(x)=g(x)$ $\int g(x)\mathrm {d} x=f(x)+C$
$\int 1\ \mathrm {d} x=x+C$
$\int a\ \mathrm {d} x=ax+C$
$\int x^{n}\mathrm {d} x={\frac {x^{n+1}}{n+1}}+C;\ n\neq -1$
$\int \sin {x}\ \mathrm {d} x=-\cos {x}+C$
$\int \cos {x}\ \mathrm {d} x=\sin {x}+C$
$\int \sec ^{2}{x}\ \mathrm {d} x=\tan {x}+C$
$\int \csc ^{2}{x}\ \mathrm {d} x=-\cot {x}+C$
$\int \sec {x}\tan {x}\ \mathrm {d} x=\sec {x}+C$
$\int \csc {x}\cot {x}\ \mathrm {d} x=-\csc {x}+C$
$\int {\frac {1}{x}}\ \mathrm {d} x=\ln |x|+C$
$\int \mathrm {e} ^{x}\mathrm {d} x=\mathrm {e} ^{x}+C$
$\int a^{x}\mathrm {d} x={\frac {a^{x}}{\ln a}}+C;\ a>0,\ a\neq 1$
$\int {\frac {1}{\sqrt {a^{2}-x^{2}}}}\ \mathrm {d} x=\arcsin \left({\frac {x}{a}}\right)+C$
$\int {\frac {1}{a^{2}+x^{2}}}\ \mathrm {d} x={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C$

Смотрите также

Примечания

^ Первообразные также называются общими интегралами , а иногда и интегралами . Последний термин является общим и относится не только к неопределенным интегралам (первообразным), но и к определенным интегралам . Когда слово интеграл используется без дополнительных уточнений, читатель должен вывести из контекста, относится ли оно к определенному или неопределенному интегралу. Некоторые авторы определяют неопределенный интеграл функции как множество ее бесконечно многих возможных первообразных. Другие определяют его как произвольно выбранный элемент этого множества. В этой статье принят последний подход. В английских учебниках по математике уровня A можно встретить термин полный примитив - L. Bostock и S. Chandler (1978) Pure Mathematics 1 ; Решение дифференциального уравнения, включающее произвольную константу, называется общим решением (или иногда полным примитивом) .

Ссылки

^ Стюарт, Джеймс (2008). Исчисление: Ранние трансцендентали (6-е изд.). Брукс/Коул . ISBN 978-0-495-01166-8.
^ Ларсон, Рон ; Эдвардс, Брюс Х. (2009). Исчисление (9-е изд.). Брукс/Коул . ISBN 978-0-547-16702-2.
^ ab "4.9: Первообразные". Mathematics LibreTexts . 2017-04-27 . Получено 2020-08-18 .
^ "Первообразная и неопределенная интеграция | Brilliant Math & Science Wiki". brilliant.org . Получено 18.08.2020 .

Дальнейшее чтение

Введение в классический вещественный анализ , Карл Р. Стромберг; Уодсворт, 1981 (см. также)
Историческое эссе о непрерывности производных инструментов Дэйва Л. Ренфро

Внешние ссылки

Wolfram Integrator — бесплатная онлайн-символьная интеграция с Mathematica
Калькулятор функций от WIMS
Интеграл в HyperPhysics
Первообразные и неопределенные интегралы в Академии Хана
Интегральный калькулятор в Symbolab
Антипроизводная в Массачусетском технологическом институте
Введение в интегралы в SparkNotes
Первообразные в колледже Харви Мадда

[1] Первообразные также называются общими интегралами , а иногда и интегралами . Последний термин является общим и относится не только к неопределенным интегралам (первообразным), но и к определенным интегралам . Когда слово интеграл используется без дополнительных уточнений, читатель должен вывести из контекста, относится ли оно к определенному или неопределенному интегралу. Некоторые авторы определяют неопределенный интеграл функции как множество ее бесконечно многих возможных первообразных. Другие определяют его как произвольно выбранный элемент этого множества. В этой статье принят последний подход. В английских учебниках по математике уровня A можно встретить термин полный примитив - L. Bostock и S. Chandler (1978) Pure Mathematics 1 ; Решение дифференциального уравнения, включающее произвольную константу, называется общим решением (или иногда полным примитивом) .

[2] Стюарт, Джеймс (2008). Исчисление: Ранние трансцендентали (6-е изд.). Брукс/Коул . ISBN 978-0-495-01166-8.

[3] Ларсон, Рон ; Эдвардс, Брюс Х. (2009). Исчисление (9-е изд.). Брукс/Коул . ISBN 978-0-547-16702-2.

[:1-4] "4.9: Первообразные". Mathematics LibreTexts . 2017-04-27 . Получено 2020-08-18 .

[5] "Первообразная и неопределенная интеграция | Brilliant Math & Science Wiki". brilliant.org . Получено 18.08.2020 .