Функция Вольтерра

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Volterra's function" – news · newspapers · books · scholar · JSTOR (August 2024) (Learn how and when to remove this message)

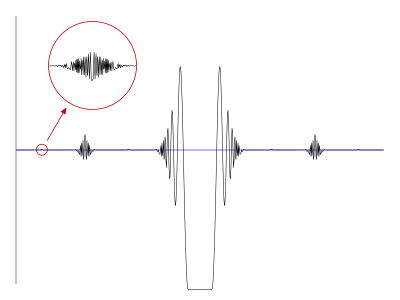
В математике функция Вольтерры , названная в честь Вито Вольтерры , представляет собой действительную функцию V, определенную на действительной прямой R со следующей любопытной комбинацией свойств:

• V дифференцируемо всюду​
• Производная V ′ ограничена всюду
• Производная не интегрируема по Риману .

Функция определяется с использованием множества Смита–Вольтерры–Кантора и «копий» функции, определенной для и . Построение V начинается с определения наибольшего значения x в интервале [0, 1/8], для которого f ′( x ) = 0. Как только это значение (скажем, x ₀ ) определено, расширьте функцию вправо с постоянным значением f ( x ₀ ) до точки 1/8 включительно. Как только это будет сделано, можно создать зеркальное отображение функции, начиная с точки 1/4 и простираясь вниз к 0. Эта функция будет определена как 0 вне интервала [0, 1/4]. Затем мы переводим эту функцию в интервал [3/8, 5/8], так что результирующая функция, которую мы называем f ₁ , будет ненулевой только на среднем интервале дополнения множества Смита–Вольтерры–Кантора. Чтобы построить f ₂ , затем f ′ рассматривается на меньшем интервале [0,1/32], усеченном в последнем месте, производная равна нулю, расширенном и зеркально отображенном так же, как и раньше, и две переведенные копии полученной функции добавляются к f ₁ для получения функции f ₂ . Затем функция Вольтерры получается путем повторения этой процедуры для каждого интервала, удаленного при построении множества Смита–Вольтерры–Кантора; другими словами, функция V является пределом последовательности функций f ₁ , f ₂ , ...${\displaystyle f(x)=x^{2}\sin(1/x)}$${\displaystyle x\neq 0}$${\displaystyle f(0)=0}$

Функция Вольтерры дифференцируема всюду, как и f (определенная выше). Можно показать, что f ′( x ) = 2 x sin(1/ x ) - cos(1/ x ) для x ≠ 0, что означает, что в любой окрестности нуля существуют точки, где f ′ принимает значения 1 и −1. Таким образом, существуют точки, где V ′ принимает значения 1 и −1 в каждой окрестности каждой из конечных точек интервалов, удаленных при построении множества Смита–Вольтерры–Кантора S . Фактически, V ′ разрывна в каждой точке S , хотя сама V дифференцируема в каждой точке S , с производной 0. Однако V ′ непрерывна на каждом интервале, удаленном при построении S , поэтому множество разрывов V ′ равно S .

Так как множество Смита–Вольтерры–Кантора S имеет положительную меру Лебега , это означает, что V ′ разрывно на множестве положительной меры. По критерию Лебега интегрируемости Римана , V ′ не интегрируемо по Риману. Если бы кто-то повторил построение функции Вольтерры с обычным множеством Кантора меры 0 C вместо «толстого» (положительной меры) множества Кантора S , то он получил бы функцию со многими похожими свойствами, но тогда производная была бы разрывной на множестве меры 0 C вместо множества положительной меры S , и поэтому результирующая функция имела бы производную, интегрируемую по Риману.

• Основная теорема исчисления

• Борьба с фундаментальной теоремой исчисления: функция Вольтерра Архивировано 23.11.2020 на Wayback Machine , доклад Дэвида Мариуса Брессо
• Пример Вольтерры производной, которая не интегрируется Архивировано 03.03.2016 на Wayback Machine ( PPT ), доклад Дэвида Мариуса Брессо