Моноидальная категория

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2025) (Learn how and when to remove this message)

В математике моноидальная категория ( или тензорная категория ) — это категория, снабженная бифунктором .${\displaystyle \mathbf {C} }$

${\displaystyle \otimes :\mathbf {C} \times \mathbf {C} \to \mathbf {C} }$

, который ассоциативен с точностью до естественного изоморфизма , и объект I , который является как левой, так и правой идентичностью для ⊗, снова с точностью до естественного изоморфизма. Связанные естественные изоморфизмы подчиняются определенным условиям когерентности , которые гарантируют, что все соответствующие диаграммы коммутируют .

Обычное тензорное произведение превращает векторные пространства , абелевы группы , R -модули или R -алгебры в моноидальные категории. Моноидальные категории можно рассматривать как обобщение этих и других примеров. Каждая ( малая ) моноидальная категория может также рассматриваться как « категоризация » базового моноида , а именно моноида, элементы которого являются классами изоморфизма объектов категории, а бинарная операция задается тензорным произведением категории.

Совсем другое применение, для которого моноидальные категории можно считать абстракцией, — это система типов данных , закрытая относительно конструктора типа , который берет два типа и строит агрегатный тип. Типы служат объектами, а ⊗ — конструктором агрегата. Ассоциативность с точностью до изоморфизма — это тогда способ выражения того, что различные способы агрегирования одних и тех же данных, такие как и , хранят одну и ту же информацию, даже если агрегатные значения не обязательно должны быть одинаковыми. Агрегатный тип может быть аналогичен операции сложения (тип sum) или умножения (тип product). Для типа product объектом идентичности является unit , поэтому существует только один житель типа, и поэтому произведение с ним всегда изоморфно другому операнду. Для типа sum объектом идентичности является тип void , который не хранит никакой информации, и невозможно обратиться к жильцам. Концепция моноидальной категории не предполагает, что значения таких агрегатных типов могут быть разобраны; Напротив, она обеспечивает основу, объединяющую классическую и квантовую теорию информации. ^[1]${\displaystyle ((a,b),c)}$${\displaystyle (a,(b,c))}$${\displaystyle ()}$

В теории категорий моноидальные категории могут использоваться для определения понятия моноидного объекта и связанного с ним действия над объектами категории. Они также используются при определении обогащенной категории .

Моноидальные категории имеют многочисленные приложения за пределами собственно теории категорий. Они используются для определения моделей для мультипликативного фрагмента интуиционистской линейной логики . Они также формируют математическую основу топологического порядка в физике конденсированного состояния . Сплетенные моноидальные категории имеют приложения в квантовой информации , квантовой теории поля и теории струн .

Моноидальная категория — это категория, снабженная моноидальной структурой. Моноидальная структура состоит из следующих элементов:${\displaystyle \mathbf {C} }$

• бифунктор , называемый моноидальным произведением , ^[2] или тензорным произведением ,${\displaystyle \otimes \colon \mathbf {C} \times \mathbf {C} \to \mathbf {C} }$
• объект, называемый моноидальной единицей , ^[2] единичный объект или тождественный объект ,${\displaystyle I}$
• три естественных изоморфизма, подчиненных определенным условиям когерентности, выражающим тот факт, что тензорная операция:
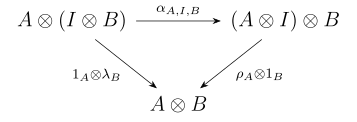
  • ассоциативен: существует естественный (в каждом из трех аргументов , , ) изоморфизм , называемый ассоциатором , с компонентами ,${\displaystyle A}$${\displaystyle B}$${\displaystyle C}$${\displaystyle \alpha }$${\displaystyle \alpha _{A,B,C}\colon A\otimes (B\otimes C)\cong (A\otimes B)\otimes C}$
  • имеет как левую, так и правую тождественность: существуют два естественных изоморфизма и , называемые соответственно левым и правым унитором , с компонентами и .${\displaystyle I}$${\displaystyle \lambda }$${\displaystyle \rho }$${\displaystyle \lambda _{A}\colon I\otimes A\cong A}$${\displaystyle \rho _{A}\colon A\otimes I\cong A}$

Обратите внимание, что хороший способ запомнить, как и действуют, — это аллитерация: Лямбда , , отменяет тождество слева , тогда как Ро , , отменяет тождество справа .${\displaystyle \lambda }$${\displaystyle \rho }$${\displaystyle \lambda }$${\displaystyle \rho }$

Условия когерентности этих естественных преобразований следующие:

• для всех , , и в , пятиугольная диаграмма${\displaystyle A}$${\displaystyle B}$${\displaystyle C}$${\displaystyle D}$${\displaystyle \mathbf {C} }$

ездит на работу ;

• для всех и в , треугольная диаграмма${\displaystyle A}$${\displaystyle B}$${\displaystyle \mathbf {C} }$

ездит на работу.

Строгая моноидальная категория — это категория, для которой естественные изоморфизмы α , λ и ρ являются тождествами. Каждая моноидальная категория моноидально эквивалентна строгой моноидальной категории.

• Любая категория с конечными произведениями может рассматриваться как моноидальная с произведением как моноидальным произведением и конечным объектом как единицей. Такая категория иногда называется декартовой моноидальной категорией . Например:
  • Множество — категория множеств , единицей которых является декартово произведение, причем единицей служит любое конкретное одноэлементное множество.
  • Cat , категория малых категорий с категорией продукта , где категория с одним объектом и только его идентификационной картой является единицей.
• Дуально, любая категория с конечными копроизведениями является моноидальной с копроизведением как моноидальным произведением и исходным объектом как единицей. Такая моноидальная категория называется кокартовой моноидальной
• R -Mod , категория модулей над коммутативным кольцом R , является моноидальной категорией с тензорным произведением модулей ⊗ _{R ,} служащим моноидальным произведением, и кольцом R (рассматриваемым как модуль над собой), служащим единицей. В качестве особых случаев имеются:
  • K -Vect , категория векторных пространств над полем K , в которой одномерное векторное пространство K служит единицей.
  • Ab — категория абелевых групп , единицей которой служит группа целых чисел Z.
• Для любого коммутативного кольца R категория R -алгебр моноидальна с тензорным произведением алгебр в качестве произведения и R в качестве единицы.
• Категория точечных пространств (ограниченная, например, компактно порожденными пространствами ) является моноидальной, причем произведением служит смэш- произведение, а единицей служит 0-точечная сфера (двухточечное дискретное пространство).
• Категория всех эндофункторов в категории C является строго моноидальной категорией с композицией функторов в качестве произведения и тождественным функтором в качестве единицы.
• Так же, как для любой категории E полная подкатегория, охватываемая любым заданным объектом, является моноидом, так же и для любой 2-категории E и любого объекта C в Ob( E ), полная 2-подкатегория E , охватываемая { C }, является моноидальной категорией. В случае E = Cat мы получаем пример эндофункторов выше.
• Ограниченные сверху полурешетки встреч являются строго симметричными моноидальными категориями : произведением является встреча, а единица является верхним элементом.
• Любой обычный моноид является малой моноидальной категорией с множеством объектов , только тождествами для морфизмов , как тензорное произведение и как его тождественный объект. Наоборот, множество классов изоморфизма (если такое имеет смысл) моноидальной категории является моноидом относительно тензорного произведения.${\displaystyle (M,\cdot ,1)}$${\displaystyle M}$${\displaystyle \cdot }$${\displaystyle 1}$
• Любой коммутативный моноид может быть реализован как моноидальная категория с одним объектом. Напомним, что категория с одним объектом — это то же самое, что и обычный моноид. Согласно аргументу Экмана-Хилтона , добавление другого моноидального произведения требует, чтобы произведение было коммутативным.${\displaystyle (M,\cdot ,1)}$${\displaystyle M}$

Из трех определяющих условий когерентности следует, что большой класс диаграмм (т. е. диаграмм, морфизмы которых построены с использованием , , , тождеств и тензорного произведения) коммутирует: это « теорема когерентности » Маклейна . Иногда неточно утверждают, что все такие диаграммы коммутируют. ^{[ необходима цитата ]}${\displaystyle \alpha }$${\displaystyle \lambda }$${\displaystyle \rho }$

Существует общее понятие моноидного объекта в моноидальной категории, которое обобщает обычное понятие моноида из абстрактной алгебры . Обычные моноиды — это в точности моноидные объекты в декартовой моноидальной категории Set . Кроме того, любая (малая) строгая моноидальная категория может рассматриваться как моноидный объект в категории категорий Cat (оснащенный моноидальной структурой, индуцированной декартовым произведением).

Моноидальные функторы — это функторы между моноидальными категориями, которые сохраняют тензорное произведение, а моноидальные естественные преобразования — это естественные преобразования между теми функторами, которые «совместимы» с тензорным произведением.

Каждую моноидальную категорию можно рассматривать как категорию B (∗, ∗) бикатегории B с единственным объектом, обозначаемым ∗.

Концепция категории C, обогащенная моноидальной категорией M, заменяет понятие множества морфизмов между парами объектов в C понятием M -объекта морфизмов между любыми двумя объектами в C.

Для каждой категории C свободную строгую моноидальную категорию Σ( C ) можно построить следующим образом:

• его объектами являются списки (конечные последовательности) A ₁ , ..., A _n объектов C ;
• стрелки между двумя объектами A ₁ , ..., A _m и B ₁ , ..., B _n существуют только если m = n , и тогда стрелки являются списками (конечными последовательностями) стрелок f 1 _: A 1 _→ B 1 _, ..., f _n : An _→ B _n из C ;
• тензорное произведение двух объектов A ₁ , ..., A _n и B ₁ , ..., B _m является конкатенацией A ₁ , ..., A _n , B ₁ , ..., B _m двух списков, и, аналогично, тензорное произведение двух морфизмов задается конкатенацией списков. Идентичным объектом является пустой список.

Эту операцию Σ, отображающую категорию C в Σ( C ), можно расширить до строгой 2- монады на Cat .

• Если в моноидальной категории и естественно изоморфны способом, совместимым с условиями когерентности, мы говорим о сплетенной моноидальной категории . Если, кроме того, этот естественный изоморфизм является своим собственным обратным, мы имеем симметричную моноидальную категорию .${\displaystyle A\otimes B}$${\displaystyle B\otimes A}$
• Замкнутая моноидальная категория — это моноидальная категория, в которой функтор имеет правый сопряженный , который называется «внутренним Hom-функтором» . Примерами служат декартово замкнутые категории, такие как Set , категория множеств, и компактные замкнутые категории , такие как FdVect , категория конечномерных векторных пространств.${\displaystyle X\mapsto X\otimes A}$${\displaystyle X\mapsto \mathrm {Hom} _{\mathbf {C} }(A,X)}$
• Автономные категории (или компактные замкнутые категории , или жесткие категории ) — это моноидальные категории, в которых существуют двойственные категории с хорошими свойствами; они абстрагируют идею FdVect .
• Кинжальные симметричные моноидальные категории , снабженные дополнительным функтором кинжала, абстрагирующие идею FdHilb , конечномерных гильбертовых пространств. К ним относятся компактные категории кинжала .
• Таннакиановские категории — это моноидальные категории, обогащенные над полем, которые очень похожи на категории представлений линейных алгебраических групп .

Предупорядоченный моноид — это моноидальная категория , в которой для каждых двух объектов существует не более одного морфизма в C . В контексте предпорядков морфизм иногда обозначается . Свойства рефлексивности и транзитивности порядка, определенные в традиционном смысле, включены в категориальную структуру посредством тождественного морфизма и формулы композиции в C , соответственно. Если и , то объекты изоморфны , что обозначается .${\displaystyle c,c'\in \mathrm {Ob} (\mathbf {C} )}$${\displaystyle c\to c'}$${\displaystyle c\to c'}$${\displaystyle c\leq c'}$${\displaystyle c\leq c'}$${\displaystyle c'\leq c}$${\displaystyle c,c'}$${\displaystyle c\cong c'}$

Введение моноидальной структуры в предпорядок C включает построение

• объект , называемый моноидальной единицей , и${\displaystyle I\in \mathbf {C} }$
• функтор , обозначаемый как " ", называемый моноидальным умножением .${\displaystyle \mathbf {C} \times \mathbf {C} \to \mathbf {C} }$${\displaystyle \;\cdot \;}$

${\displaystyle I}$и должны быть унитарными и ассоциативными с точностью до изоморфизма, что означает: ${\displaystyle \cdot }$

${\displaystyle (c_{1}\cdot c_{2})\cdot c_{3}\cong c_{1}\cdot (c_{2}\cdot c_{3})}$и .${\displaystyle I\cdot c\cong c\cong c\cdot I}$

Так как · — функтор,

если и тогда .${\displaystyle c_{1}\to c_{1}'}$${\displaystyle c_{2}\to c_{2}'}$${\displaystyle (c_{1}\cdot c_{2})\to (c_{1}'\cdot c_{2}')}$

Другие условия когерентности моноидальных категорий выполняются посредством структуры предпорядка, поскольку каждая диаграмма коммутирует в предпорядке.

Натуральные числа являются примером моноидального предпорядка: наличие как моноидной структуры (с использованием + и 0), так и структуры предпорядка (с использованием ≤) образует моноидальный предпорядок, поскольку и подразумевает . ${\displaystyle m\leq n}$${\displaystyle m'\leq n'}$${\displaystyle m+m'\leq n+n'}$

Свободный моноид на некотором порождающем множестве создает моноидальный предпорядок, создавая полусистему Туэ .

• Скелет (теория категорий)
• Сферическая категория
• Моноидальное действие категории

• Медиа, связанные с категорией «Моноидальный» на Wikimedia Commons