5-ти ячеечный

5-клеточный
(4-симплексный)
5-клеточный ; (4-симплексный)
	3D-проекция 5-клеточного объекта, совершающего простое вращение
Тип	Выпуклый правильный 4-мерный многогранник
Символ Шлефли	{3,3,3}
Диаграмма Коксетера
Клетки	5 {3,3}
Лица	10 {3}
Края	10
Вершины	5
Вершинная фигура	; ( тетраэдр )
Петри полигон	пятиугольник
Группа Коксетера	А 4 , [3,3,3]
Двойной	Самодвойственный
Характеристики	выпуклый , изогональный , изотоксальный , изоэдральный
Единый индекс	1

Четырехмерный аналог тетраэдра

В геометрии 5-ячейка — это выпуклый 4-многогранник с символом Шлефли {3,3,3}. Это 5-вершинный четырехмерный объект, ограниченный пятью тетраэдрическими ячейками. Он также известен как C ₅ , гипертетраэдр , ' пентахорон , ^[1] пентатоп , пентаэдроид , ^[2] тетраэдрическая пирамида или 4- симплекс (многогранник Коксетера ), ^[3] простейший возможный выпуклый 4-многогранник и аналогичен тетраэдру в трех измерениях и треугольнику в двух измерениях. 5-ячейка — это 4-мерная пирамида с тетраэдрическим основанием и четырьмя тетраэдрическими сторонами. $\alpha _{4}$

Правильный 5-ячейник ограничен пятью правильными тетраэдрами и является одним из шести правильных выпуклых 4-многогранников (четырехмерных аналогов Платоновых тел ). Правильный 5-ячейник можно построить из правильного тетраэдра, добавив пятую вершину, удаленную на одну длину ребра от всех вершин тетраэдра. Это невозможно сделать в трехмерном пространстве. Правильный 5-ячейник является решением задачи: сделать 10 равносторонних треугольников, все одинакового размера, используя 10 спичек, где каждая сторона каждого треугольника равна ровно одной спичке, и ни один из треугольников и спичек не пересекает друг друга. Не существует решения в трех измерениях.

Характеристики

5-ячейка — это 4-мерный симплекс , простейший возможный 4-многогранник . Другими словами, 5-ячейка — это полихор, аналогичный тетраэдру в высокой размерности. ^[4] Он образован любыми пятью точками, которые не все находятся в одной гиперплоскости (как тетраэдр образован любыми четырьмя точками, которые не все находятся в одной плоскости, а треугольник образован любыми тремя точками, которые не все находятся на одной прямой). Любые такие пять точек составляют 5-ячейку, хотя обычно не правильную 5-ячейку. Правильная 5-ячейка не встречается ни в одном из других правильных выпуклых 4-многогранников, за исключением одного: 600-вершинная 120-ячейка является соединением 120 правильных 5-ячеек.

5-ячейка является самодвойственной , то есть ее двойственный многогранник является самой 5-ячейкой. ^[5] Ее максимальное пересечение с 3-мерным пространством — треугольная призма . Ее дихоральный угол равен . ^[6] ${\textstyle \arccos(-1/4)\approx 75.52^{\circ }}$

Он является первым в последовательности из 6 выпуклых правильных 4-мерных многогранников, в порядке увеличения объема при заданном радиусе или числе вершин. ^[7]

Выпуклая оболочка двух 5-ячеек в дуальной конфигурации представляет собой двуклиновидный 30-ячеечный многоугольник , двойственный усеченному 5-ячеечному многоугольнику .

Как конфигурация

Эта матрица конфигурации представляет собой 5-ячейку. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа говорят, сколько элементов каждого элемента встречается во всей 5-ячейке. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним. Матрица этого самодвойственного многогранника идентична своему повороту на 180 градусов. ^[8]K - грани можно читать как строки слева от диагонали, в то время как k -фигуры читаются как строки после диагонали. ^[9]

к -лицо	ф _к	ф ₀	ф ₁	ф ₂	ф ₃	к -фиги
( )	ф ₀	5	4	6	4	{3,3}
{ }	ф ₁	2	10	3	3	{3}
{3}	ф ₂	3	3	10	2	{ }
{3,3}	ф ₃	4	6	4	5	( )

Все эти элементы пятиячейки перечислены в диаграмме Венна из 5 точек Бранко Грюнбаума , которая буквально представляет собой иллюстрацию правильной пятиячейки в проекции на плоскость.

Геодезические и вращения

3D-проекция 5-клеточного объекта, совершающего двойной поворот .

5-ячейка имеет только двуугольные центральные плоскости через вершины. Она имеет 10 двуугольных центральных плоскостей, где каждая пара вершин является ребром, а не осью 5-ячейки. Каждая двуугольная плоскость ортогональна 3 другим, но не полностью ортогональна ни одной из них. Характерное изоклиническое вращение 5-ячейки имеет в качестве пар инвариантных плоскостей эти 10 двуугольных плоскостей и их полностью ортогональные центральные плоскости, которые являются плоскостями 0-угольников, которые не пересекают ни одной из вершин 5-ячейки.

Есть только два способа сделать контур 5-ячейки через все 5 вершин вдоль 5 ребер, поэтому есть два дискретных расслоения Хопфа больших двуугольников 5-ячейки. Каждое из двух расслоений соответствует паре лево-правых изоклинных вращений, каждое из которых вращает все 5 вершин в контуре периода 5. 5-ячейка имеет только две различные изоклины периода 5 (те окружности, которые проходят через все 5 вершин), каждая из которых действует как единственная изоклина правого вращения и единственная изоклина левого вращения в двух различных расслоениях.

Ниже визуализировано вращающееся 5-ячеечное тело с четвертым измерением, сжатым и отображенным в цвете. Тор Клиффорда изображен в прямоугольной (оборачивающей) форме.

Визуализация 4D вращений
Простое вращение в плоскости XY
Простое вращение в плоскости ZW
Двойное вращение в плоскостях XY и ZW с угловыми скоростями в соотношении 4:3
Левое изоклиническое вращение
Правое изоклиническое вращение

Прогнозы

Плоскость Коксетера A ₄ проецирует 5-ячейку в правильный пятиугольник и пентаграмму . Проекция плоскости Коксетера A ₃ 5-ячейки — это проекция квадратной пирамиды . Проекция плоскости Коксетера A ₂ правильной 5-ячейки — это проекция треугольной бипирамиды (два тетраэдра, соединенные лицом к лицу) с двумя противоположными вершинами в центре.

ортографические проекции
Самолет _{Коксетера}	А ₄	А ₃	А ₂
График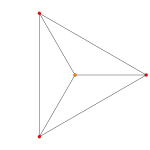
Диэдральная симметрия	[5]	[4]	[3]

Проекции в 3 измерения
Проекция вершины первой 5-ячейки в 3 измерения имеет тетраэдрическую проекционную оболочку. Ближайшая вершина 5-ячейки проецируется в центр тетраэдра, как показано здесь красным. Самая дальняя ячейка проецируется на саму тетраэдрическую оболочку, в то время как остальные 4 ячейки проецируются на 4 сплющенных тетраэдрических области, окружающих центральную вершину.	Проекция 5-клетки в 3 измерениях с ребром имеет треугольную дипирамидальную оболочку. Ближайшее ребро (показано здесь красным) проецируется на ось дипирамиды, а три окружающие его клетки проецируются на 3 тетраэдрических объема, расположенных вокруг этой оси под углом 120 градусов друг к другу. Оставшиеся 2 клетки проецируются на две половины дипирамиды и находятся на дальней стороне пентатопа.
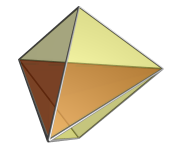Проекция 5-клетки на 3 измерения «face-first» также имеет треугольную дипирамидальную оболочку. Ближайшая грань показана здесь красным. Две ячейки, которые встречаются на этой грани, проецируются на две половины дипирамиды. Остальные три ячейки находятся на дальней стороне пентатопа с точки зрения 4D и для ясности отброшены с изображения. Они расположены вокруг центральной оси дипирамиды, как и в проекции «edge-first».	Проекция ячейки-первая 5-ячейки в 3 измерения имеет тетраэдрическую оболочку. Ближайшая ячейка проецируется на всю оболочку и, с точки зрения 4D, закрывает остальные 4 ячейки; поэтому они здесь не визуализируются.

Неправильный 5-клеточный

В случае симплексов, таких как 5-ячейка, определенные нерегулярные формы в некотором смысле более фундаментальны, чем правильная форма. Хотя правильные 5-ячейки не могут заполнить 4-пространство или правильные 4-многогранники, существуют нерегулярные 5-ячейки, которые это делают. Эти характерные 5-ячейки являются фундаментальными доменами различных групп симметрии , которые порождают различные 4-многогранники.

Ортосхемы

4-ортосхема — это 5-ячейка, в которой все 10 граней являются прямоугольными треугольниками . (5 вершин образуют 5 тетраэдрических ячеек, гранями соединенных друг с другом, с общим числом 10 ребер и 10 треугольных граней.) Ортосхема — это неправильный симплекс , который является выпуклой оболочкой дерева , в котором все ребра взаимно перпендикулярны. В 4-мерной ортосхеме дерево состоит из четырех перпендикулярных ребер, соединяющих все пять вершин линейным путем, который делает три прямоугольных поворота. Элементы ортосхемы также являются ортосхемами (так же как элементы правильного симплекса также являются правильными симплексами). Каждая тетраэдрическая ячейка 4-ортосхемы является 3-ортосхемой , а каждая треугольная грань является 2-ортосхемой (прямоугольным треугольником).

Ортосхемы являются характеристическими симплексами правильных многогранников, поскольку каждый правильный многогранник генерируется отражениями в ограничивающих гранях его конкретной характеристической ортосхемы. ^[10] Например, частный случай 4-ортосхемы с перпендикулярными ребрами одинаковой длины является характеристической ортосхемой 4-куба (также называемого тессерактом или 8-ячейкой ), 4-мерного аналога 3-мерного куба. Если три перпендикулярных ребра 4-ортосхемы имеют единичную длину, то все ее ребра имеют длину √ 1 , √ 2 , √ 3 или √ 4 , в точности длины хорд единичного 4-куба (длины ребер 4-куба и его различных диагоналей). Следовательно, эта 4-ортосхема вписывается в 4-куб, а 4-куб (как и всякий правильный выпуклый многогранник) может быть разрезан на экземпляры его характерной ортосхемы .

3-ортосхему легко проиллюстрировать, но 4-ортосхему визуализировать сложнее. 4-ортосхема — это тетраэдрическая пирамида с 3-ортосхемой в качестве основания. Она имеет на четыре ребра больше, чем 3-ортосхема, соединяя четыре вершины основания с ее вершиной (пятой вершиной 5-ячейки). Выберите любую из 3-ортосхем из шести, показанных на иллюстрации 3-куба. Обратите внимание, что она касается четырех из восьми вершин куба, и эти четыре вершины связаны путем из 3 ребер, который делает два прямоугольных поворота. Представьте, что эта 3-ортосхема является основанием 4-ортосхемы, так что из каждой из этих четырех вершин невидимое ребро 4-ортосхемы соединяется с пятой вершиной вершины (которая находится вне 3-куба и вообще не отображается на иллюстрации). Хотя все четыре дополнительных ребра достигают одной и той же вершины вершины, все они будут иметь разную длину. Первое из них, на одном конце ортогонального пути из 3-ребер, расширяет этот путь четвертым ортогональным √ 1 ребром, делая третий поворот на 90 градусов и достигая перпендикулярно в четвертое измерение к вершине. Второе из четырех дополнительных ребер является √ 2 диагональю грани куба (не изображенного 3-куба, а другого из восьми 3-кубов тессеракта). Третье дополнительное ребро — это диагональ √ 3 куба 3 (опять же, не исходного проиллюстрированного куба 3). Четвертое дополнительное ребро (на другом конце ортогонального пути) — это длинный диаметр самого тессеракта длиной √ 4 . Оно проходит через точный центр тессеракта к вершине -антиподу (вершине противолежащего куба 3), которая является вершиной. Таким образом, характерная 5-ячейка куба 4 имеет четыре ребра √ 1 , три ребра √ 2 , два ребра √ 3 и одно ребро √ 4 .

4-кубовыйможно разбить на 24 такие 4-ортосхемы восемью различными способами, с шестью 4-ортосхемами, окружающими каждый из четырех ортогональных √ 4 длинных диаметров тессеракта. 4-куб также может быть разрезан на 384 меньших экземпляра этой же самой характерной 4-ортосхемы, только одним способом, всеми его гиперплоскостями симметрии одновременно, которые делят его на 384 4-ортосхемы, которые все встречаются в центре 4-куба.

В более общем смысле, любой правильный многогранник может быть разрезан на g экземпляров его характеристической ортосхемы, которые все встречаются в центре правильного многогранника. ^[11] Число g — это порядок многогранника, число отраженных экземпляров его характеристической ортосхемы, которые составляют многогранник, когда один экземпляр зеркально-поверхностной ортосхемы отражается в своих собственных гранях. В более общем смысле, характеристические симплексы способны заполнять однородные многогранники, поскольку они обладают всеми необходимыми элементами многогранника. Они также обладают всеми необходимыми углами между элементами (от 90 градусов и ниже). Характеристические симплексы являются генетическими кодами многогранников: подобно швейцарскому армейскому ножу , они содержат по одному экземпляру всего необходимого для построения многогранника путем репликации.

Каждый правильный многогранник, включая правильный 5-ячейковый, имеет свою характерную ортосхему. Существует 4-ортосхема, которая является характерной 5-ячейкой правильного 5-ячейника . Это тетраэдрическая пирамида, основанная на характерном тетраэдре правильного тетраэдра . Правильный 5-ячейникможно разделить на 120 экземпляров этой характерной 4-ортосхемытолько одним способом, всеми его гиперплоскостями симметрии одновременно, которые делят его на 120 4-ортосхем, которые все встречаются в центре правильной 5-ячейки.

Характеристики обычного 5-клеточного ^[12]
	край ^[13]	дуга		двугранный ^[14]
𝒍	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	104°30′40″	$\pi -2{\text{𝜂}}$	75°29′20″	$\pi -2{\text{𝟁}}$

𝟀	${\sqrt {\tfrac {1}{10}}}\approx 0.316$	75°29′20″	$2{\text{𝜂}}$	60°	${\tfrac {\pi }{3}}$
𝝉 ^[а]	${\sqrt {\tfrac {1}{30}}}\approx 0.183$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	60°	${\tfrac {\pi }{3}}$
𝟁	${\sqrt {\tfrac {2}{15}}}\approx 0.103$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	60°	${\tfrac {\pi }{3}}$

$_{0}R^{3}/l$	${\sqrt {\tfrac {3}{20}}}\approx 0.387$	75°29′20″	$2{\text{𝜂}}$	90°	${\tfrac {\pi }{2}}$
$_{1}R^{3}/l$	${\sqrt {\tfrac {1}{20}}}\approx 0.224$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	90°	${\tfrac {\pi }{2}}$
$_{2}R^{3}/l$	${\sqrt {\tfrac {1}{60}}}\approx 0.129$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	90°	${\tfrac {\pi }{2}}$

$_{0}R^{4}/l$	${\sqrt {1}}=1.0$
$_{1}R^{4}/l$	${\sqrt {\tfrac {3}{8}}}\approx 0.612$
$_{2}R^{4}/l$	${\sqrt {\tfrac {1}{6}}}\approx 0.408$
$_{3}R^{4}/l$	${\sqrt {\tfrac {1}{16}}}=0.25$

${\text{𝜼}}$		37°44′40″	${\tfrac {{\text{arc sec }}4}{2}}$

Характеристическая 5-ячейка (4-ортосхема) правильной 5-ячейки имеет на четыре ребра больше, чем ее базовый характеристический тетраэдр (3-ортосхема), которые соединяют четыре вершины основания с его вершиной (пятая вершина 4-ортосхемы, в центре правильной 5-ячейки). Четыре ребра каждой 4-ортосхемы, которые встречаются в центре правильного 4-политопа, имеют неравную длину, поскольку они являются четырьмя характеристическими радиусами правильного 4-политопа: радиусом вершины, радиусом центра ребра, радиусом центра грани и радиусом центра ячейки. Если правильная 5-ячейка имеет единичный радиус и длину ребра , десять ребер ее характеристической 5-ячейки имеют длины , , вокруг ее внешней прямоугольной грани (ребра, противоположные характеристическим углам 𝟀, 𝝉, 𝟁), ^[a] плюс , , (остальные три ребра внешней грани 3-ортосхемы характеристического тетраэдра, которые являются характеристическими радиусами правильного тетраэдра), плюс , , , (ребра, которые являются характеристическими радиусами правильной 5-ячейки). Путь из 4 ребер вдоль ортогональных ребер ортосхемы - это , , , , сначала от правильной 5-ячеечной вершины к правильному 5-ячеечному ребровому центру, затем поворот на 90° к правильному 5-ячеечному центру грани, затем поворот на 90° к правильному 5-ячеечному тетраэдрическому центру ячейки, затем поворот на 90° к правильному 5-ячеечному центру. ${\sqrt {\tfrac {5}{2}}}$ ${\sqrt {\tfrac {1}{10}}}$ ${\sqrt {\tfrac {1}{30}}}$ ${\sqrt {\tfrac {2}{15}}}$ ${\sqrt {\tfrac {3}{20}}}$ ${\sqrt {\tfrac {1}{20}}}$ ${\sqrt {\tfrac {1}{60}}}$ ${\sqrt {1}}$ ${\sqrt {\tfrac {3}{8}}}$ ${\sqrt {\tfrac {1}{6}}}$ ${\sqrt {\tfrac {1}{16}}}$ ${\sqrt {\tfrac {1}{30}}}$ ${\sqrt {\tfrac {2}{15}}}$ ${\sqrt {\tfrac {1}{60}}}$ ${\sqrt {\tfrac {1}{16}}}$

Изометрии

Существует много форм с более низкой симметрией 5-ячейки, включая те, которые встречаются в виде вершинных фигур однородного многогранника :

Симметрия	[3,3,3] Заказ 120	[3,3,1] Заказ 24	[3,2,1] Заказ 12	[3,1,1] Заказ 6	~[5,2] ⁺ Заказ 10
Имя	Обычный 5-ти ячеечный	Тетраэдрическая пирамида		Треугольная пирамидальная пирамида
Шлефли	{3,3,3}	{3,3}∨( )	{3}∨{ }	{3}∨( )∨( )
Пример вершинной фигуры	5-симплекс	Усеченный 5-симплекс	Усеченный 5-симплекс	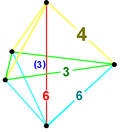Усеченный 5-симплекс	Усеченные 4-симплексные соты

Тетраэдрическая пирамида является частным случаем 5-ячеечной , многогранной пирамиды , построенной как основание правильного тетраэдра в 3-мерной гиперплоскости , и вершина над гиперплоскостью. Четыре стороны пирамиды сделаны из треугольных пирамидальных ячеек .

Многие однородные 5-мерные многогранники имеют вершинные фигуры в виде тетраэдрических пирамид с символами Шлефли ( )∨{3,3}.

Симметрия [3,3,1], порядок 24
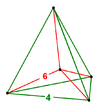Имя Коксетер	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	т{3,3,3,3}	т{4,3,3,3}	т{3,4,3,3}
Диаграмма Шлегеля

Другие однородные 5-многогранники имеют нерегулярные 5-клеточные вершинные фигуры. Симметрия вершинной фигуры однородного многогранника представлена путем удаления окольцованных узлов диаграммы Коксетера.

Симметрия	[3,2,1], порядок 12		[3,1,1], порядок 6		[2 ⁺ ,4,1], порядок 8	[2,1,1], порядок 4
Шлефли	{3}∨{ }		{3}∨( )∨( )		{ }∨{ }∨( )
Диаграмма Шлегеля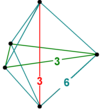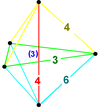
Имя Коксетер	т ₁₂ α ₅	т ₁₂ γ ₅	т ₀₁₂ α ₅	т ₀₁₂ γ ₅	т ₁₂₃ α ₅	т ₁₂₃ γ ₅

Симметрия	[2,1,1], порядок 2			[2 ⁺ ,1,1], порядок 2	[ ] ⁺ , заказ 1
Шлефли	{ }∨( )∨( )∨( )			( )∨( )∨( )∨( )∨( )
Диаграмма Шлегеля
Имя Коксетер	т ₀₁₂₃ α ₅	т ₀₁₂₃ γ ₅	т ₀₁₂₃ β ₅	т ₀₁₂₃₄ α ₅	т ₀₁₂₃₄ γ ₅

Строительство

Как спираль Бурдейка-Коксетера

5-ячейка может быть построена как спираль Бурдейка–Коксетера из пяти соединенных тетраэдров, сложенных в 4-мерное кольцо. ^[15] 10 треугольных граней можно увидеть в 2D-сети внутри треугольной мозаики с 6 треугольниками вокруг каждой вершины, хотя сворачивание в 4-мерное пространство приводит к совпадению ребер. Фиолетовые ребра образуют правильный пятиугольник , который является многоугольником Петри 5-ячейки. Синие ребра соединяют каждую вторую вершину, образуя пентаграмму , которая является многоугольником Клиффорда 5-ячейки. Синие ребра пентаграммы являются хордами изоклины 5-ячейки , круговой траектории вращения, которую принимают ее вершины во время изоклинического вращения , также известного как смещение Клиффорда .

Сеть

Когда сеть из пяти тетраэдров складывается в 4-мерном пространстве так, что каждый тетраэдр гранью связан с четырьмя другими, то полученная 5-ячейка имеет в общей сложности 5 вершин, 10 ребер и 10 граней. Четыре ребра сходятся в каждой вершине, а три тетраэдрические ячейки сходятся в каждом ребре. Это делает шесть тетраэдров ее ячейкой . ^[6]

Координаты

Простейший набор декартовых координат : (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (𝜙,𝜙,𝜙,𝜙), с длиной ребра 2 √ 2 , где 𝜙 — золотое сечение . ^[16] Хотя эти координаты не центрированы в начале координат, вычитание из каждой из них переводит центр описанной окружности 4-многогранника в начало координат с радиусом , со следующими координатами: $(1,1,1,1)/(2-{\tfrac {1}{\phi }})$ $2(\phi -1/(2-{\tfrac {1}{\phi }}))={\sqrt {\tfrac {16}{5}}}\approx 1.7888$

\left({\tfrac {2}{\phi }}-3,1,1,1\right)/({\tfrac {1}{\phi }}-2)

\left(1,{\tfrac {2}{\phi }}-3,1,1\right)/({\tfrac {1}{\phi }}-2)

\left(1,1,{\tfrac {2}{\phi }}-3,1\right)/({\tfrac {1}{\phi }}-2)

\left(1,1,1,{\tfrac {2}{\phi }}-3\right)/({\tfrac {1}{\phi }}-2)

\left({\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }}\right)/({\tfrac {1}{\phi }}-2)

Следующий набор координат с центром в начале координат, с тем же радиусом и длиной ребра, что и выше, можно рассматривать как гиперпирамиду с правильным тетраэдрическим основанием в трехмерном пространстве:

\left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)

\left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)

\left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)

\left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)

\left(0,0,0,{\frac {4}{\sqrt {5}}}\right)

Масштабирование этих или предыдущего набора координат дает единичный радиус с центром в начале координат и регулярными 5-ячейками с длинами ребер . Гиперпирамида имеет координаты: ${\tfrac {\sqrt {5}}{4}}$ ${\sqrt {\tfrac {5}{2}}}$

\left({\sqrt {5}},{\sqrt {5}},{\sqrt {5}},-1\right)/4

\left({\sqrt {5}},-{\sqrt {5}},-{\sqrt {5}},-1\right)/4

\left(-{\sqrt {5}},{\sqrt {5}},-{\sqrt {5}},-1\right)/4

\left(-{\sqrt {5}},-{\sqrt {5}},{\sqrt {5}},-1\right)/4

\left(0,0,0,1\right)

Координаты вершин другого правильного 5-ячейкового многоугольника с центром в начале координат, длиной ребра 2 и радиусом равны: ${\sqrt {\tfrac {8}{5}}}\approx 1.265$

\left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)

\left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)

\left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)

\left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)

Масштабируя их до единичного радиуса и длины ребра, получаем: ${\sqrt {\tfrac {5}{8}}}$ ${\sqrt {\tfrac {5}{2}}}$

\left({\sqrt {3}},{\sqrt {5}},{\sqrt {10}},\pm {\sqrt {30}}\right)/(4{\sqrt {3}})

\left({\sqrt {3}},{\sqrt {5}},-{\sqrt {40}},0\right)/(4{\sqrt {3}})

\left({\sqrt {3}},-{\sqrt {45}},0,0\right)/(4{\sqrt {3}})

\left(-1,0,0,0\right)

Вершины 4-симплекса (с ребром √ 2 и радиусом 1) можно проще построить на гиперплоскости в 5-пространстве как (отдельные) перестановки (0,0,0,0,1) или (0,1,1,1,1); в этих позициях это фасетка , соответственно, 5-ортоплекса или выпрямленного пентеракта .

Сложный

Соединение двух 5-ячеек в дуальных конфигурациях можно увидеть в этой проекции плоскости Коксетера A5 с красными и синими 5-ячеечными вершинами и ребрами. Это соединение имеет симметрию [[3,3,3]], порядок 240. Пересечение этих двух 5-ячеек является однородной битусеченной 5-ячейкой .=∩.

Это соединение можно рассматривать как 4D-аналог 2D- гексаграммы { ⁠6/2⁠ } и трехмерное соединение двух тетраэдров .

Связанные многогранники и соты

Пентахорон (5-клеточный) — простейший из 9 однородных полихоров, построенных из группы Коксетера [3,3,3] .

Шлефли	{3,3,3}	т{3,3,3}	г{3,3,3}	рр{3,3,3}	2т{3,3,3}	тр{3,3,3}	т _0,3 {3,3,3}	т _0,1,3 {3,3,3}	т _0,1,2,3 {3,3,3}
Коксетер
Шлегель

1 _k2 фигур в n измерениях
Космос	Конечный						Евклидов	Гиперболический
н	3	4	5	6	7	8	9	10
Группа Коксетера	Э ₃ =А ₂ А ₁	Э ₄ =А ₄	Э ₅ =Д ₅	Е ₆	Е ₇	Е ₈	Э ₉ = = Э ₈⁺ ${\tilde {E}}_{8}$	Е ₁₀ = = Е ₈⁺⁺ ${\bar {T}}_{8}$
Диаграмма Коксетера
Симметрия (порядок)	[3 ^−1,2,1 ]	[3 ^0,2,1 ]	[3 ^1,2,1 ]	[[3 ^2,2,1 ]]	[3 ^3,2,1 ]	[3 ^4,2,1 ]	[3 ^5,2,1 ]	[3 ^6,2,1 ]
Заказ	12	120	1,920	103,680	2,903,040	696,729,600	∞
График							-	-
Имя	1 _−1,2	102	1 ₁₂	1 ₂₂	1 ₃₂	1 ₄₂	1 ₅₂	1 ₆₂

2 _{k 1} фигур в n измерениях
Космос	Конечный						Евклидов	Гиперболический
н	3	4	5	6	7	8	9	10
Группа Коксетера	Э ₃ =А ₂ А ₁	Э ₄ =А ₄	Э ₅ =Д ₅	Е ₆	Е ₇	Е ₈	Э ₉ = = Э ₈⁺ ${\tilde {E}}_{8}$	Е ₁₀ = = Е ₈⁺⁺ ${\bar {T}}_{8}$
Диаграмма Коксетера
Симметрия	[3 ^−1,2,1 ]	[3 ^0,2,1 ]	[[3 ^1,2,1 ]]	[3 ^2,2,1 ]	[3 ^3,2,1 ]	[3 ^4,2,1 ]	[3 ^5,2,1 ]	[3 ^6,2,1 ]
Заказ	12	120	384	51,840	2,903,040	696,729,600	∞
График							-	-
Имя	2 _−1,1	2 ₀₁	2 ₁₁	2 ₂₁	2 ₃₁	2 ₄₁	2 ₅₁	2 ₆₁

Он находится в последовательности {p,3,3} правильных многогранников с тетраэдрической вершинной фигурой : тессеракт {4,3,3} и 120-ячейковый {5,3,3} евклидова 4-мерного пространства, а также шестиугольные соты мозаики {6,3,3} гиперболического пространства.

{p,3,3} многогранники
Космос	С ³			Н ³
Форма	Конечный			Паракомпактный	Некомпактный
Имя	{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	... {∞,3,3}
Изображение
Клетки {p,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Это один из трех {3,3,p} правильных 4-многогранников с тетраэдрическими ячейками, наряду с 16-ячеечным {3,3,4} и 600-ячеечным {3,3,5}. Тетраэдрические соты {3,3,6} порядка 6 гиперболического пространства также имеют тетраэдрические ячейки.

{3,3,p} многогранники
Космос	С ³			Н ³
Форма	Конечный			Паракомпактный	Некомпактный
Имя	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Изображение
Вершинная фигура	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Он самодвойственен, как и 24-клеточный {3,4,3}, имеющий палиндромный символ Шлефли {3,p,3} .

{3, p ,3} многогранники
Космос	С ³		Н ³
Форма	Конечный		Компактный	Паракомпактный	Некомпактный
{3, п ,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Изображение
Клетки	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Вершинная фигура	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{p,3,p} обычные соты
Космос	С ³	Евклидово E ³	Н ³
Форма	Конечный	Аффинный	Компактный	Паракомпактный	Некомпактный
Имя	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	... {∞,3,∞}
Изображение
Клетки	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Вершинная фигура	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Примечания

^ ab (Коксетер 1973) использует греческую букву 𝝓 (фи) для обозначения одного из трех характеристических углов 𝟀, 𝝓, 𝟁 правильного многогранника. Поскольку 𝝓 обычно используется для обозначения константы золотого сечения ≈ 1,618, для которой Коксетер использует 𝝉 (тау), мы меняем соглашения Коксетера на противоположные и используем 𝝉 для обозначения характеристического угла.

Цитаты

^ Джонсон 2018, стр. 249.
^ Гика 1977, стр. 68.
^ Coxeter 1973, стр. 120, §7.2. см. иллюстрацию Рис. 7.2 А.
^ Миядзаки и Исии 2021, стр. 46.
^ Диудеа 2018, стр. 41.
^ Аб Акияма, Хитотумату и Сато 2012.
↑ Coxeter 1973, стр. 292–293, Таблица I(ii): Шестнадцать правильных многогранников { p,q,r } в четырех измерениях.
^ Коксетер 1973, стр. 12, §1.8. Конфигурации.
^ «Перо».
↑ Coxeter 1973, стр. 198–202, §11.7 Правильные фигуры и их усечения.
^ Ким и Роте 2016, стр. 17–20, §10 Классификация Кокстера четырехмерных точечных групп.
^ Коксетер 1973, стр. 292–293, Таблица I(ii); «5-клеточная, 𝛼 ₄ ».
^ Коксетер 1973, стр. 139, §7.9 Характерный симплекс.
^ Коксетер 1973, стр. 290, Таблица I(ii); «двугранные углы».
^ Банчофф 2013.
^ Коксетер 1991, стр. 30, §4.2. Кристаллографические правильные многогранники.

Ссылки

Акияма, Джин; Хитотумату, Син; Сато, Икуро (2012). «Определение номеров элементов правильных многогранников». Геометрии Дедиката . 159 : 89–97. дои : 10.1007/s10711-011-9647-3.
Diudea, MV (2018). Многослойные полиэдральные кластеры. Углеродные материалы: химия и физика. Том 10. Springer . doi :10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
Гика, Матила (1977). Геометрия искусства и жизни. Dover Publications . ISBN 978-0-486-23542-4.
Джонсон, Н. В. (2018). "Конечные группы симметрии, 11.5 Сферические группы Коксетера". Геометрии и преобразования . Издательство Кембриджского университета. ISBN 978-1-107-10340-5.
Миядзаки, К.; Ишии, М. (2021). «Симметрия в проекции 4-мерного регулярного полихора». В Darvas, György (ред.). Комплексные симметрии. doi : 10.1007/978-3-030-88059-0. ISBN 978-3-030-88059-0.
Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
HSM Коксетер :
- Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Довер.
  - стр. 120, §7.2. см. иллюстрацию Рис. 7.2 А
  - стр. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерности (n≥5)
- Коксетер, HSM (1991), Регулярные комплексные многогранники (2-е изд.), Кембридж: Cambridge University Press
- Калейдоскопы: избранные труды Х. С. М. Коксетера, под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
  - (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
Ким, Хеуна; Роте, Г. (2016). «Проверка конгруэнтности множеств точек в 4 измерениях». arXiv : 1603.07269 [cs.CG].
Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 _n1 )
Норман Джонсон Однородные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
Banchoff, Thomas F. (2013). "Торические разложения правильных многогранников в 4-пространстве". В Senechal, Marjorie (ред.). Shaping Space . Springer New York. стр. 257–266. doi :10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8.

Внешние ссылки

Вайсштейн, Эрик В. «Пентатоп». MathWorld .
Клитцинг, Ричард. «4D однородные многогранники (полихоры) x3o3o3o - ручка».
Der 5-Zeller (5-клеточные) Правильные многогранники Марко Мёллера в R ⁴ (немецкий)
Джонатан Бауэрс, Регулярная полихора
Апплеты Java3D
пирохорон

в т е Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
Семья	А _н	Б _н	Я ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ф ₄ / Соль ₂	Н _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16-ячеечный • Тессеракт	Демитессеракт	24-ячеечный	120-ячеечный • 600-ячеечный
Однородный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Однородный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Однородный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Однородный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Однородный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Однородный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Однородный n - многогранник	н - симплекс	n - ортоплекс • n - куб	н - демикуб	1 _к2 • 2 _к1 • к ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[reversed_greek_symbols-15] (Коксетер 1973) использует греческую букву 𝝓 (фи) для обозначения одного из трех характеристических углов 𝟀, 𝝓, 𝟁 правильного многогранника. Поскольку 𝝓 обычно используется для обозначения константы золотого сечения ≈ 1,618, для которой Коксетер использует 𝝉 (тау), мы меняем соглашения Коксетера на противоположные и используем 𝝉 для обозначения характеристического угла.

[FOOTNOTEJohnson2018249-1] Джонсон 2018, стр. 249.

[FOOTNOTEGhyka1977[httpsbooksgooglecombooksidh1Wm6tHAKHcCpgPA68_68]-2] Гика 1977, стр. 68.

[FOOTNOTECoxeter1973120§7.2._see_illustration_Fig_7.2<small>A</small>-3] Coxeter 1973, стр. 120, §7.2. см. иллюстрацию Рис. 7.2 А.

[FOOTNOTEMiyazakiIshii2021[httpsbooksgooglecombooksidd2VXEAAAQBAJpgPA46_46]-4] Миядзаки и Исии 2021, стр. 46.

[FOOTNOTEDiudea2018[httpsbooksgooglecombooksidp_06DwAAQBAJpgPA41_41]-5] Диудеа 2018, стр. 41.

[FOOTNOTEAkiyamaHitotumatuSato2012-6] Аб Акияма, Хитотумату и Сато 2012.

[FOOTNOTECoxeter1973292–293Table_I(ii):_The_sixteen_regular_polytopes_{''p,q,r''}_in_four_dimensions-7] Coxeter 1973, стр. 292–293, Таблица I(ii): Шестнадцать правильных многогранников { p,q,r } в четырех измерениях.

[FOOTNOTECoxeter197312§1.8._Configurations-8] Коксетер 1973, стр. 12, §1.8. Конфигурации.

[9] «Перо».

[FOOTNOTECoxeter1973198–202§11.7_Regular_figures_and_their_truncations-10] Coxeter 1973, стр. 198–202, §11.7 Правильные фигуры и их усечения.

[FOOTNOTEKimRote201617–20§10_The_Coxeter_Classification_of_Four-Dimensional_Point_Groups-11] Ким и Роте 2016, стр. 17–20, §10 Классификация Кокстера четырехмерных точечных групп.

[FOOTNOTECoxeter1973292–293Table_I(ii);_"5-cell,_𝛼<sub>4</sub>"-12] Коксетер 1973, стр. 292–293, Таблица I(ii); «5-клеточная, 𝛼 ₄ ».

[FOOTNOTECoxeter1973139§7.9_The_characteristic_simplex-13] Коксетер 1973, стр. 139, §7.9 Характерный симплекс.

[FOOTNOTECoxeter1973290Table_I(ii);_"dihedral_angles"-14] Коксетер 1973, стр. 290, Таблица I(ii); «двугранные углы».

[FOOTNOTEBanchoff2013-16] Банчофф 2013.

[FOOTNOTECoxeter199130§4.2._The_Crystallographic_regular_polytopes-17] Коксетер 1991, стр. 30, §4.2. Кристаллографические правильные многогранники.