Треугольная мозаика бесконечного порядка

Треугольная мозаика бесконечного порядка
Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая правильная мозаика
Конфигурация вершины	3 ∞
Символ Шлефли	{3,∞}
Символ Витхоффа	∞ | 3 2
Диаграмма Коксетера
Группа симметрии	[∞,3], (*∞32)
Двойной	Апейрогональная мозаика порядка 3
Характеристики	Вершинно-транзитивный , реберно-транзитивный , гране-транзитивный

В геометрии треугольная мозаика бесконечного порядка — это правильная мозаика гиперболической плоскости с символом Шлефли {3,∞}. Все вершины идеальны , расположены в «бесконечности» и видны на границе гиперболической дисковой проекции Пуанкаре.

Форма с более низкой симметрией имеет чередующиеся цвета и представлена ​​циклическим символом {(3,∞,3)},. Мозаика также представляет собой фундаментальные области симметрии *∞∞∞ , которые можно увидеть с помощью 3 цветов линий, представляющих 3 зеркала конструкции.

Альтернативная цветная мозаика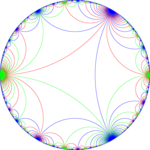

*∞∞∞ симметрия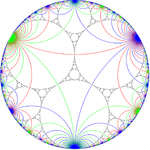

Аполлоново покрытие с симметрией *∞∞∞

Эта мозаика топологически связана как часть последовательности правильных многогранников с символом Шлефли {3,p}.

* n 32 мутация симметрии правильных мозаик: {3, n } в т е
Сферический				Евклид.	Компактный гипер.		Парако.	Некомпактный гиперболический
3.3	3 3	3 4	3 5	3 6	3 7	3 8	3∞	3 12i	3 9i	3 6и	3 3и

Паракомпактные однородные мозаики в семействе [∞,3] в т е
Симметрия: [∞,3], (*∞32)							[∞,3] + (∞32)	[1 + ,∞,3] (*∞33)		[∞,3 + ] (3*∞)
		=	=	=				= или	= или	=
{∞,3}	т{∞,3}	г{∞,3}	т{3,∞}	{3,∞}	рр{∞,3}	тр{∞,3}	ср{∞,3}	ч{∞,3}	ч 2 {∞,3}	с{3,∞}
Равномерные дуалы
V∞3	V3.∞.∞	V(3.∞) 2	В6.6.∞	В3 ∞	В4.3.4.∞	В4.6.∞	В3.3.3.3.∞	V(3.∞) 3		В3.3.3.3.3.∞

Паракомпактные гиперболические однородные мозаики в семействе [(∞,3,3)] в т е
Симметрия: [(∞,3,3)], (*∞33)							[(∞,3,3)] + , (∞33)
(∞,∞,3)	т 0,1 (∞,3,3)	т 1 (∞,3,3)	т 1,2 (∞,3,3)	т2(∞,3,3)	т 0,2 (∞,3,3)	т 0,1,2 (∞,3,3)	с(∞,3,3)
Двойные плитки
V(3.∞) 3	V3.∞.3.∞	V(3.∞) 3	В3.6.∞.6	В(3,3) ∞	В3.6.∞.6	В6.6.∞	В3.3.3.3.3.∞

Неправильную треугольную мозаику бесконечного порядка можно получить с помощью рекурсивного процесса из центрального треугольника, как показано здесь:

На Викискладе есть медиафайлы по теме Треугольная мозаика бесконечного порядка .

• Тетраэдрические соты бесконечного порядка
• Список правильных многогранников
• Список однородных плоских мозаик
• Мозаики правильных многоугольников
• Треугольная мозаика
• Однородные мозаики на гиперболической плоскости

• Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN  978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
• "Глава 10: Регулярные соты в гиперболическом пространстве". Красота геометрии: Двенадцать эссе . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN  99035678.

• Вайсштейн, Эрик В. "Гиперболическая мозаика". MathWorld .
• Вайсштейн, Эрик В. "Гиперболический диск Пуанкаре". MathWorld .