Ранжированные пары

Совместная серия «Политика и экономика»
Социальный выбор и избирательные системы
Социальный выбор Конструкция механизма Сравнительная политология Сравнение Список  ( по странам )
Методы с одним победителем Single vote - plurality methods First preference plurality (FPP) Two-round (US: Jungle primary) Partisan primary Instant-runoff UK: Alternative vote (AV) US: Ranked-choice (RCV) Condorcet methods Condorcet-IRV Round-robin voting Minimax Schulze Ranked pairs Maximal lottery Positional voting Plurality (el. IRV) Borda count (el. Baldwin) Antiplurality (el. Coombs) Cardinal voting Score voting Approval voting Majority judgment STAR voting
Proportional representation Party-list Apportionment Highest averages Largest remainders National remnant Biproportional List type Closed list Open list Panachage List-free PR Localized list Quota-remainder methods Hare STV Schulze STV CPO-STV Quota Borda Approval-based committees Thiele's method Phragmen's method Expanding approvals rule Method of equal shares Fractional social choice Direct representation Interactive representation Liquid democracy Fractional approval voting Maximal lottery Random ballot Semi-proportional representation Cumulative SNTV Limited voting
Mixed systems By results of combination Mixed-member majoritarian Mixed-member proportional By mechanism of combination Non-compensatory Parallel (superposition) Coexistence Conditional Fusion (majority bonus) Compensatory Seat linkage system UK: 'AMS' NZ: 'MMP' Vote linkage system Negative vote transfer Mixed ballot Supermixed systems Dual-member proportional Rural–urban proportional Majority jackpot By ballot type Single vote Double simultaneous vote Dual-vote
Paradoxes and pathologies Spoiler effects Spoiler effect Cloning paradox Frustrated majorities paradox Center squeeze Pathological response Perverse response Best-is-worst paradox No-show paradox Multiple districts paradox Strategic voting Lesser evil voting Exaggeration Truncation Turkey-raising Paradoxes of majority rule Tyranny of the majority Discursive dilemma Conflicting majorities paradox
Social and collective choice Impossibility theorems Arrow's theorem Majority impossibility Moulin's impossibility theorem McKelvey–Schofield chaos theorem Gibbard's theorem Positive results Median voter theorem Condorcet's jury theorem May's theorem Condorcet dominance theorems Harsanyi's utilitarian theorem VCG mechanism Quadratic voting
Politics portal Economics portal Mathematics portal
v t e

Ранжированные пары ( RP ), также известные как метод Тайдмана , представляют собой турнирную систему рейтингового голосования, впервые предложенную Николаусом Тайдманом в 1987 году. ^{[1] [2]}

Если есть кандидат, который предпочтительнее других кандидатов, при сравнении по очереди с каждым из остальных, процедура ранжированных пар гарантирует победу этого кандидата. Таким образом, процедура ранжированных пар соответствует критерию победителя Кондорсе (и, как следствие, считается методом Кондорсе ). ^[3]

Ранжированные пары начинаются с кругового турнира , где сравниваются преимущества один на один для каждой возможной пары кандидатов, чтобы найти кандидата, предпочитаемого большинством ; если такой кандидат существует, он немедленно избирается. В противном случае, если есть цикл Кондорсе — последовательность, похожая на камень-ножницы-бумага A > B > C > A — цикл прерывается путем отбрасывания «самых слабых» выборов в цикле, т. е. тех, которые ближе всего к равенству. ^[4]

Процедура ранжирования пар выглядит следующим образом:

1. Рассмотрите каждую пару кандидатов по круговой системе и рассчитайте попарный перевес для каждого в поединке один на один.
2. Отсортируйте пары по ( абсолютному ) перевесу победителей, от наибольшего к наименьшему.
3. Двигаясь вниз по списку, проверьте, не приведет ли добавление каждого матча к созданию цикла . Если это так, вычеркните выборы; это будут выборы в цикле с наименьшим перевесом в победе (почти равные шансы). ^{[примечание 1]}

В конце этой процедуры все циклы будут устранены, оставив уникального победителя, который победит во всех оставшихся матчах один на один. Отсутствие циклов означает, что кандидаты могут быть ранжированы напрямую на основе оставшихся матчей.

Предположим, что Теннесси проводит выборы по месту расположения своей столицы . Население сосредоточено вокруг четырех крупных городов. Все избиратели хотят, чтобы столица была как можно ближе к ним. Возможны следующие варианты:

• Мемфис , крупнейший город, но далеко от других (42% избирателей)
• Нэшвилл , недалеко от центра штата (26% избирателей)
• Чаттануга , немного восточнее (15% избирателей)
• Ноксвилл , далеко на северо-востоке (17% избирателей)

Предпочтения избирателей каждого региона таковы:

Результаты представлены в следующей таблице:

• [A] обозначает избирателей, которые предпочли кандидата, указанного в заголовке столбца, кандидату, указанному в заголовке строки.
• [B] указывает избирателей, которые предпочли кандидата, указанного в заголовке строки, кандидату, указанному в заголовке столбца.

Сначала перечислите все пары и определите победителя:

Затем голоса сортируются. Наибольшее большинство — «Чаттануга против Ноксвилла»; 83% избирателей предпочитают Чаттанугу. Таким образом, пары сверху будут сортироваться следующим образом:

Затем пары блокируются по порядку, пропуская любые пары, которые могли бы создать цикл:

• Блокировка Чаттануги над Ноксвиллом.
• Сравняем счет «Нэшвилл» с «Ноксвиллом».
• Совместная победа «Нэшвилла» над «Чаттанугой».
• Сравняем счет «Нэшвилл» с «Мемфисом».
• Заблокируйте Чаттанугу против Мемфиса.
• Победа над Мемфисом в Ноксвилле.

В этом случае ни одна из пар не создает циклов, поэтому каждая из них заблокирована.

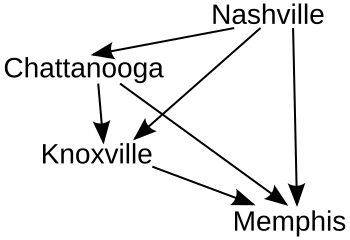
Каждое "закрепление" добавляло бы еще одну стрелку к графику, показывающему связь между кандидатами. Вот окончательный график (где стрелки указывают от победителя).

В этом примере победителем с использованием процедуры ранжированных пар является Нэшвилл. За Нэшвиллом следуют Чаттануга, Ноксвилл и Мемфис на втором, третьем и четвертом местах соответственно.

В примере выборов победителем оказывается Нэшвилл. Это справедливо для любого метода Кондорсе .

При системе относительного большинства и некоторых других системах Мемфис выиграл бы выборы, имея больше всего людей, даже несмотря на то, что Нэшвилл выиграл все смоделированные парные выборы вчистую. Использование мгновенного голосования в этом примере привело бы к победе Ноксвилла, даже несмотря на то, что больше людей предпочли Нэшвилл, чем Ноксвилл.

Из формальных критериев голосования метод ранжированных пар проходит критерий большинства , критерий монотонности , критерий Смита (который подразумевает критерий Кондорсе ), критерий проигравшего Кондорсе и критерий независимости клонов . Ранжированные пары не проходят критерий согласованности и критерий участия . Хотя ранжированные пары не полностью независимы от нерелевантных альтернатив , они все же удовлетворяют локальной независимости от нерелевантных альтернатив и независимости от доминируемых Смитом альтернатив , то есть они, вероятно, примерно удовлетворяют IIA «на практике».

Ранжированные пары не соответствуют независимости нерелевантных альтернатив , как и все другие ранжированные системы голосования . Однако метод придерживается менее строгого свойства, иногда называемого независимостью альтернатив, доминируемых Смитом (ISDA). Он гласит, что если один кандидат (X) выигрывает выборы и добавляется новая альтернатива (Y), X победит на выборах, если Y не входит в набор Смита . ISDA подразумевает критерий Кондорсе.

В следующей таблице сравниваются ранжированные пары с другими методами выборов с одним победителем:

• Описания методов рейтингового голосования Роба ЛеГранда
• Пример реализации JS Асафа Хаддада
• Парный рейтинг рубинового камня от Бала Паранджа
• Реализация ранжированных пар Tideman на PHP с использованием маржинальной прибыли
• Реализация ранжированных пар на Rust от Кори Диксона