Шестиугольник

Правильный шестиугольник
Правильный шестиугольник
Тип	Правильный многоугольник
Ребра и вершины	6
Символ Шлефли	{6}, т{3}
Диаграммы Кокстера–Дынкина
Группа симметрии	Двугранный (D 6 ), порядок 2×6
Внутренний угол ( градусы )	120°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии шестиугольник (от греч. ἕξ , hex , что означает «шесть», и γωνία , gonía , что означает «угол, угол») — шестиугольник . [ ^1] Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника равна 720°.

Правильный шестиугольник имеет символ Шлефли {6} ^[2] и может быть также построен как усеченный равносторонний треугольник t {3}, который чередует два типа ребер.

Правильный шестиугольник определяется как шестиугольник, который является как равносторонним , так и равноугольным . Он является бицентрическим , что означает, что он является как вписанным (имеет описанную окружность), так и касательным (имеет вписанную окружность).

Общая длина сторон равна радиусу описанной окружности или описанной окружности , который равен произведению апофемы (радиуса вписанной окружности ). Все внутренние углы равны 120 градусам . Правильный шестиугольник имеет шесть вращательных симметрий ( вращательная симметрия шестого порядка ) и шесть зеркальных симметрий ( шесть осей симметрии ), составляющих диэдральную группу D6 . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, в _два раза больше длины одной стороны. Из этого можно видеть, что треугольник с вершиной в центре правильного шестиугольника и разделяющий одну сторону с шестиугольником, является равносторонним , и что правильный шестиугольник можно разбить на шесть равносторонних треугольников.${\displaystyle {\tfrac {2}{\sqrt {3}}}}$

Подобно квадратам и равносторонним треугольникам , правильные шестиугольники подходят друг к другу без каких-либо зазоров, чтобы замостить плоскость (три шестиугольника встречаются в каждой вершине), и поэтому полезны для построения мозаик . Ячейки пчелиных сот являются шестиугольными по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного правильной треугольной решетки представляет собой сотовую мозаику шестиугольников.

Максимальный диаметр (соответствующий длинной диагонали шестиугольника), D , в два раза больше максимального радиуса или радиуса описанной окружности , R , который равен длине стороны, t . Минимальный диаметр или диаметр вписанной окружности (расстояние между параллельными сторонами, расстояние между плоскостями, короткая диагональ или высота при опирании на плоское основание), d , в два раза больше минимального радиуса или вписанного радиуса , r . Максимумы и минимумы связаны одним и тем же коэффициентом:

${\displaystyle {\frac {1}{2}}d=r=\cos(30^{\circ })R={\frac {\sqrt {3}}{2}}R={\frac {\sqrt {3}}{2}}t}$   и, аналогично,${\displaystyle d={\frac {\sqrt {3}}{2}}D.}$

Площадь правильного шестиугольника

${\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\[3pt]&={\frac {3{\sqrt {3}}}{8}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {3}}{2}}d^{2}\\[3pt]&\приблизительно 2,598R^{2}\приблизительно 3,464r^{2}\\&\приблизительно 0,6495D^{2}\приблизительно 0,866d^{2}.\end{aligned}}}$

Для любого правильного многоугольника площадь также может быть выражена через апофему a и периметр p . Для правильного шестиугольника они задаются как a = r и p , так что${\displaystyle {}=6R=4r{\sqrt {3}}}$

${\displaystyle {\begin{aligned}A&={\frac {ap}{2}}\\&={\frac {r\cdot 4r{\sqrt {3}}}{2}}=2r^{2}{\sqrt {3}}\\&\approx 3.464r^{2}.\end{aligned}}}$

Правильный шестиугольник заполняет часть описанной около него окружности .${\displaystyle {\tfrac {3{\sqrt {3}}}{2\pi }}\approx 0,8270}$

Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описанной окружности между B и C, то PE + PF = PA + PB + PC + PD .

Из отношения радиуса описанной окружности к радиусу вписанной окружности следует , что отношение высоты к ширине правильного шестиугольника составляет 1:1,1547005; то есть шестиугольник с большой диагональю 1,0000000 будет иметь расстояние 0,8660254 или cos(30°) между параллельными сторонами.

Для произвольной точки на плоскости правильного шестиугольника с радиусом описанной окружности , расстояния которой до центра тяжести правильного шестиугольника и его шести вершин равны и соответственно, имеем ^[3]${\displaystyle R}$${\displaystyle L}$${\displaystyle d_{i}}$

${\displaystyle d_{1}^{2}+d_{4}^{2}=d_{2}^{2}+d_{5}^{2}=d_{3}^{2}+d_{6}^{2}=2\left(R^{2}+L^{2}\right),}$

${\displaystyle d_{1}^{2}+d_{3}^{2}+d_{5}^{2}=d_{2}^{2}+d_{4}^{2}+d_{6}^{2}=3\left(R^{2}+L^{2}\right),}$

${\displaystyle d_{1}^{4}+d_{3}^{4}+d_{5}^{4}=d_{2}^{4}+d_{4}^{4}+d_{6}^{4}=3\left(\left(R^{2}+L^{2}\right)^{2}+2R^{2}L^{2}\right).}$

Если — расстояния от вершин правильного шестиугольника до любой точки его описанной окружности, то ^[3]${\displaystyle d_{i}}$

${\displaystyle \left(\sum _{i=1}^{6}d_{i}^{2}\right)^{2}=4\sum _{i=1}^{6}d_{i}^{4}.}$

Примеры шестиугольников по симметрии
r12 обычный и4 d6 изотоксальный g6 направленный p6 изогональный д2 g2 общий параллелогон стр2 г3 а1

Правильный шестиугольник имеет симметрию D _6. Существует 16 подгрупп. С точностью до изоморфизма их 8: сама (D ₆ ), 2 двугранные: (D _3, D ₂ ), 4 циклические : (Z ₆ , Z ₃ , Z ₂ , Z ₁ ) и тривиальная (e)

Эти симметрии выражают девять различных симметрий правильного шестиугольника. Джон Конвей маркирует их буквой и порядком группы. ^[4] r12 — полная симметрия, а a1 — отсутствие симметрии. p6 — изогональный шестиугольник, построенный тремя зеркалами, может чередовать длинные и короткие ребра, и d6 — изотоксальный шестиугольник, построенный с равными длинами ребер, но вершинами, чередующими два разных внутренних угла. Эти две формы являются дуальными друг другу и имеют половину порядка симметрии правильного шестиугольника. Формы i4 — это правильные шестиугольники, сплющенные или вытянутые вдоль одного направления симметрии. Его можно рассматривать как вытянутый ромб , в то время как d2 и p2 можно рассматривать как горизонтально и вертикально вытянутые воздушные змеи . Шестиугольники g2 с параллельными противоположными сторонами также называются шестиугольными параллелограммами .

Каждая подгруппа симметрии допускает одну или несколько степеней свободы для нерегулярных форм. Только подгруппа g6 не имеет степеней свободы, но может рассматриваться как направленные ребра .

Шестиугольники симметрии g2 , i4 , и r12 , как параллелогонов могут замостить евклидову плоскость переносом. Другие формы шестиугольников могут замостить плоскость с различными ориентациями.

стр 6 м (*632)	смм (2*22)	стр. 2 (2222)	с 31 м (3*3)	пмг (22*)		стр. (××)
р12	и4	г2	д2	д2	стр2	а1
Дих 6	Дих 2	Z2​	Дих 1			Я 1

Корни группы А2

Корни группы G2

6 корней простой группы Ли A2 , представленные диаграммой Дынкина , находятся в правильной шестиугольной форме. Два простых корня имеют угол 120° между собой.

12 корней исключительной группы Ли G2 , представленные диаграммой Дынкина также находятся в шестиугольной форме. Два простых корня двух длин имеют угол 150° между собой.

6-кубовая проекция	12 ромбовидная диссекция

Коксетер утверждает, что каждый зоногон (2 -метровый угольник, противоположные стороны которого параллельны и имеют одинаковую длину) можно разрезать на 1 ⁄ 2 m ( m − 1) параллелограммов. ^[5] В частности, это верно для правильных многоугольников с четным числом сторон, в этом случае все параллелограммы являются ромбами. Это разложение правильного шестиугольника основано на проекции многоугольника Петри куба с 3 из 6 квадратных граней. Другие параллелогоны и проективные направления куба разрезаются внутри прямоугольных кубоидов .

Разбиение шестиугольников на три ромба и параллелограмма
2D	Ромбы	Параллелограммы
	Регулярный {6}	Шестиугольные параллелогоны
3D	Квадратные лица		Прямоугольные лица
	Куб		Прямоугольный кубоид

Правильный шестиугольник имеет символ Шлефли {6}. Правильный шестиугольник является частью правильной шестиугольной мозаики {6,3} с тремя шестиугольными гранями вокруг каждой вершины.

Правильный шестиугольник также может быть создан как усеченный равносторонний треугольник с символом Шлефли t{3}. Рассматриваемая с двумя типами (цветами) ребер, эта форма имеет только симметрию D _{3 .}

Усеченный шестиугольник , t{6}, является двенадцатиугольником , {12}, с чередующимися двумя типами (цветами) ребер. Чередующийся шестиугольник, h{6}, является равносторонним треугольником , {3}. Правильный шестиугольник может быть представлен в форме звезды с равносторонними треугольниками на его ребрах, создавая гексаграмму . Правильный шестиугольник может быть разрезан на шесть равносторонних треугольников , если добавить центральную точку. Этот шаблон повторяется в правильной треугольной мозаике .

Правильный шестиугольник можно расширить до правильного двенадцатиугольника , добавляя вокруг него чередующиеся квадраты и равносторонние треугольники . Этот шаблон повторяется в ромботригексагональной мозаике .

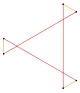Регулярный {6}	Усеченный t{3} = {6}	Гиперусеченные треугольники			Звездчатая фигура 2{3}	Усеченный t{6} = {12}	Альтернативный h{6} = {3}

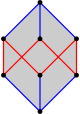Перекрещенный шестиугольник	Вогнутый шестиугольник	Самопересекающийся шестиугольник ( звездчатый многоугольник )	Расширенный центральный {6} в {12}	Косой шестиугольник внутри куба	Разрезанный {6}	проекционный октаэдр	Полный график

Существует шесть самопересекающихся шестиугольников с расположением вершин правильного шестиугольника:

Самопересекающиеся шестиугольники с правильными вершинами

Дих 2			Дих 1		Дих 3
Восьмерка	Центр-флип	Уникурсальный	Рыбий хвост	Двойной хвост	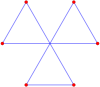Тройной хвост

От пчелиных сот до Дороги гигантов , шестиугольные узоры распространены в природе из-за их эффективности. В шестиугольной сетке каждая линия настолько коротка, насколько это возможно, если большая площадь должна быть заполнена наименьшим количеством шестиугольников. Это означает, что соты требуют меньше воска для построения и приобретают большую прочность при сжатии .

Неправильные шестиугольники с параллельными противоположными гранями называются параллелогонами и также могут замостить плоскость переносом. В трех измерениях шестиугольные призмы с параллельными противоположными гранями называются параллелоэдрами и могут замостить трехмерное пространство переносом.

Мозаики из шестиугольных призм

Форма	Шестиугольная мозаика	Шестиугольные призматические соты
Обычный
Параллелогенный

Помимо правильного шестиугольника, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, удовлетворяющий критерию Конвея , будет замощать плоскость.

Теорема Паскаля (также известная как «Теорема о мистическом гексаграмме») утверждает, что если произвольный шестиугольник вписан в любое коническое сечение и пары противоположных сторон продолжены до встречи, то три точки пересечения будут лежать на прямой линии — «линии Паскаля» этой конфигурации.

Шестиугольник Лемуана — это вписанный в окружность шестиугольник с вершинами, заданными шестью пересечениями сторон треугольника и тремя прямыми, параллельными сторонам, которые проходят через его точку симедианы .

Если последовательными сторонами циклического шестиугольника являются a , b , c , d , e , f , то три главные диагонали пересекаются в одной точке тогда и только тогда, когда ace = bdf . ^[6]

Если для каждой стороны вписанного шестиугольника смежные стороны расширены до их пересечения, образуя треугольник, внешний по отношению к данной стороне, то отрезки, соединяющие центры описанных окружностей противолежащих треугольников, являются конкурирующими . ^[7]

Если шестиугольник имеет вершины на описанной окружности остроугольного треугольника в шести точках (включая три вершины треугольника), где продолженные высоты треугольника пересекают описанную окружность, то площадь шестиугольника в два раза больше площади треугольника. ^{[8] : стр. 179}

Пусть ABCDEF — шестиугольник, образованный шестью касательными линиями конического сечения. Тогда теорема Брианшона утверждает, что три главные диагонали AD, BE и CF пересекаются в одной точке.

В шестиугольнике, который касается окружности и имеет последовательные стороны a , b , c , d , e и f , ^[9]

${\displaystyle a+c+e=b+d+f.}$

Если на каждой стороне любого шестиугольника снаружи построить равносторонний треугольник , то середины отрезков, соединяющих центры тяжести противоположных треугольников, образуют другой равносторонний треугольник. ^{[10] : Теория 1}

Косой шестиугольник — это косой многоугольник с шестью вершинами и ребрами, но не лежащий на одной плоскости. Внутренность такого шестиугольника обычно не определена. Косой зигзагообразный шестиугольник имеет вершины, чередующиеся между двумя параллельными плоскостями.

Правильный косой шестиугольник является вершинно-транзитивным с равными длинами сторон. В трех измерениях это будет зигзагообразный косой шестиугольник и его можно увидеть в вершинах и боковых ребрах треугольной антипризмы с той же D _3d , [2 ⁺ ,6] симметрией, порядка 12.

Куб и октаэдр (также как и треугольная антипризма) имеют правильные косые шестиугольники в качестве многоугольников Петри .

Косые шестиугольники на 3-х осях

Куб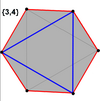

Октаэдр

Правильный косой шестиугольник является многоугольником Петри для этих правильных , однородных и двойственных многогранников и многогранников более высокой размерности, показанных в следующих косых ортогональных проекциях :

4D		5D
3-3 дуопризма	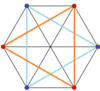3-3 дуопирамида	5-симплекс

Главная диагональ шестиугольника — это диагональ, которая делит шестиугольник на четырехугольники. В любом выпуклом равностороннем шестиугольнике (у которого все стороны равны) с общей стороной a существует ^{[11] : стр.184, #286.3} главная диагональ d ₁ такая, что

${\displaystyle {\frac {d_{1}}{a}}\leq 2}$

и главная диагональ d ₂ такая, что

${\displaystyle {\frac {d_{2}}{a}}>{\sqrt {3}}.}$

Не существует Платоновых тел, состоящих только из правильных шестиугольников, поскольку шестиугольники мозаичны , не позволяя результату «складываться». Архимедовы тела с некоторыми шестиугольными гранями — это усеченный тетраэдр , усеченный октаэдр , усеченный икосаэдр (известный как футбольный мяч и фуллерен ), усеченный кубооктаэдр и усеченный икосододекаэдр . Эти шестиугольники можно считать усеченными треугольниками с диаграммами Коксетера видаи.

Шестиугольники в архимедовых телах
Тетраэдрический	Октаэдрический		Икосаэдрический
усеченный тетраэдр	усеченный октаэдр	усеченный кубооктаэдр	усеченный икосаэдр	усеченный икосододекаэдр

Существуют и другие симметричные многогранники с вытянутыми или сплющенными шестиугольниками, например, многогранник Голдберга G(2,0):

Шестиугольники в многогранниках Голдберга
Тетраэдрический	Октаэдрический	Икосаэдрический
Тетраэдр с фаской	Куб со скошенной кромкой	Додекаэдр с фаской

Существует также 9 тел Джонсона с правильными шестиугольниками:

Тела Джонсона с шестиугольниками
треугольный купол	удлиненный треугольный купол	гироудлиненный треугольный купол
увеличенная шестиугольная призма	парадвуугольная шестиугольная призма	метабиаугментированная шестиугольная призма
триаугментированная шестиугольная призма	дополненный усеченный тетраэдр	треугольная гебесфеноротонда

Призмоиды с шестиугольниками
Шестиугольная призма	Гексагональная антипризма	Шестиугольная пирамида

Мозаики с правильными шестиугольниками
Обычный	1-униформа
{6,3}	г{6,3}	рр{6,3}	тр{6,3}
2-однородные мозаики

Спор о том, следует ли называть шестиугольники «шестиугольниками», коренится в этимологии термина. Префикс «hex-» происходит от греческого слова «hex», означающего шесть, в то время как «sex-» происходит от латинского «sex», также означающего шесть. Некоторые лингвисты и математики утверждают, что, поскольку многие английские математические термины происходят от латыни, использование «sexagon» соответствовало бы этой традиции. Исторические дискуссии восходят к 19 веку, когда математики начали стандартизировать терминологию в геометрии. Тем не менее, термин «шестиугольник» преобладает в общеупотребительном употреблении и академической литературе, укрепляя свое место в математической терминологии, несмотря на исторический аргумент в пользу «sexagon». По-прежнему сохраняется консенсус, что «шестиугольник» является подходящим термином, отражающим его греческое происхождение и устоявшееся использование в математике. (см. Numeral_prefix#Occurrences ).

• 
  Идеальная кристаллическая структура графена представляет собой гексагональную сетку.
• 
  Собранные сегменты зеркала E-ELT
• 
  Пчелиные соты
• 
  Щитки панциря черепахи
• 
  Шестиугольник Сатурна , шестиугольный рисунок облаков вокруг северного полюса планеты.
• 
  Микрофотография снежинки
• 
  Бензол , простейшее ароматическое соединение с гексагональной формой.
• 
  Шестиугольный порядок пузырьков в пене.
• 
  Кристаллическая структура молекулярного шестиугольника, состоящего из гексагональных ароматических колец.
• 
  Базальтовые колонны, образованные естественным путем из Дороги гигантов в Северной Ирландии ; большие массы должны медленно остывать, чтобы сформировать полигональную структуру изломов.
• 
  Вид с воздуха на Форт Джефферсон в национальном парке Драй-Тортугас.
• 
  Зеркало космического телескопа Джеймса Уэбба состоит из 18 шестиугольных сегментов.
• 
  Во французском языке l'Hexagone относится к метрополии Франции из-за ее неопределенно шестиугольной формы.
• 
  Гексагональный кристалл ханксита , один из многих минералов гексагональной кристаллической системы.
• 
  Шестиугольный амбар
• 
  «Хексагон» — шестиугольный театр в Рединге, Беркшир.
• 
  Шестиугольные шахматы Владислава Глинского.
• 
  Павильон в Тайваньском ботаническом саду
• 
  Шестиугольное окно

• 24-ячейка : четырехмерная фигура, которая, как и шестиугольник, имеет ортоплексные грани, является самодвойственной и заполняет евклидово пространство.
• Гексагональная кристаллическая система
• Шестиугольное число
• Шестиугольная мозаика : правильная мозаика из шестиугольников на плоскости.
• Гексаграмма : шестиконечная звезда внутри правильного шестиугольника.
• Уникурсальная гексаграмма : один путь, шестиконечная звезда, внутри шестиугольника.
• гипотеза о сотах
• Гаванна : абстрактная настольная игра, играемая на шестиугольной сетке.
• Теория центрального места

Найдите значение слова «шестиугольник» в Викисловаре, бесплатном словаре.

• Вайсштейн, Эрик В. «Шестиугольник». MathWorld .

• Определение и свойства шестиугольника с интерактивной анимацией и построением с помощью циркуля и линейки.
• Введение в гексагональную геометрию на Hexnet — веб-сайте, посвященном математике шестиугольников.
• Шестиугольники — это Bestagons на YouTube — анимированное интернет-видео о шестиугольниках от CGP Grey .