группа Лоренца
| Алгебраическая структура → Теория групп Теория групп |
|---|
 |

В физике и математике группа Лоренца — это группа всех преобразований Лоренца пространства -времени Минковского , классического и квантового описания всех (негравитационных) физических явлений . Группа Лоренца названа в честь голландского физика Хендрика Лоренца .
Например, следующие законы, уравнения и теории соблюдают симметрию Лоренца:
- Кинематические законы специальной теории относительности
- Уравнения поля Максвелла в теории электромагнетизма
- Уравнение Дирака в теории электрона
- Стандартная модель физики элементарных частиц
Группа Лоренца выражает фундаментальную симметрию пространства и времени всех известных фундаментальных законов природы . В достаточно малых областях пространства-времени, где гравитационные дисперсии пренебрежимо малы, физические законы инвариантны относительно Лоренца так же, как и специальная теория относительности.
Основные свойства
Группа Лоренца является подгруппой группы Пуанкаре — группы всех изометрий пространства - времени Минковского . Преобразования Лоренца — это, в точности, изометрии, которые оставляют начало координат фиксированным. Таким образом, группа Лоренца является подгруппой изотропии относительно начала координат группы изометрий пространства-времени Минковского. По этой причине группу Лоренца иногда называют однородной группой Лоренца , а группу Пуанкаре иногда называют неоднородной группой Лоренца . Преобразования Лоренца являются примерами линейных преобразований ; общие изометрии пространства-времени Минковского являются аффинными преобразованиями .
Определение физики
Предположим, что имеются две инерциальные системы отсчета ( t , x , y , z ) и ( t ′, x ′, y ′, z ′) и две точки P1 , P2 ; группа Лоренца — это набор всех преобразований между двумя системами отсчета, которые сохраняют скорость света, распространяющегося между двумя точками:
В матричной форме это все линейные преобразования Λ такие, что:
Их называют преобразованиями Лоренца .
Математическое определение
Математически группу Лоренца можно описать как неопределенную ортогональную группу O(1, 3) , матричную группу Ли , которая сохраняет квадратичную форму
на R 4 (векторное пространство, снабженное этой квадратичной формой, иногда записывается как R 1,3 ). Эта квадратичная форма, будучи помещена в матричную форму (см. Классическая ортогональная группа ), интерпретируется в физике как метрический тензор пространства-времени Минковского.
Математические свойства
Группа Лоренца — это шестимерная некомпактная неабелева вещественная группа Ли , которая не является связной . Четыре связных компонента не являются просто связными . [1] Компонент тождества (т. е. компонент, содержащий единичный элемент) группы Лоренца сам по себе является группой и часто называется ограниченной группой Лоренца и обозначается как SO + (1, 3) . Ограниченная группа Лоренца состоит из тех преобразований Лоренца, которые сохраняют как ориентацию пространства, так и направление времени. Ее фундаментальная группа имеет порядок 2, а ее универсальное покрытие, неопределенная спиновая группа Spin(1, 3) , изоморфно как специальной линейной группе SL(2, C ) , так и симплектической группе Sp(2, C ) . Эти изоморфизмы позволяют группе Лоренца действовать на большое количество математических структур, важных для физики, в первую очередь на спиноры . Таким образом, в релятивистской квантовой механике и в квантовой теории поля очень часто принято называть SL(2, C ) группой Лоренца, понимая, что SO + (1, 3) является ее определенным представлением (векторным представлением).
Рекуррентное представление действия группы Лоренца на пространстве Минковского использует бикватернионы , которые образуют алгебру композиции . Свойство изометрии преобразований Лоренца выполняется согласно свойству композиции .
Другим свойством группы Лоренца является конформность или сохранение углов. Лоренцовы бусты действуют посредством гиперболического вращения плоскости пространства-времени, и такие «вращения» сохраняют гиперболический угол , меру быстроты, используемую в теории относительности. Таким образом, группа Лоренца является подгруппой конформной группы пространства-времени .
Обратите внимание, что в этой статье O(1, 3) называется «группой Лоренца», SO(1, 3) — «собственной группой Лоренца», а SO + (1, 3) — «ограниченной группой Лоренца». Многие авторы (особенно в физике) используют название «группа Лоренца» для SO(1, 3) (или иногда даже SO + (1, 3) ) вместо O(1, 3) . Читая таких авторов, важно четко понимать, о ком именно они говорят.
Подключенные компоненты

Поскольку это группа Ли , группа Лоренца O(1, 3) является группой и также имеет топологическое описание как гладкое многообразие . Как многообразие, она имеет четыре связных компонента. Интуитивно это означает, что она состоит из четырех топологически разделенных частей.
Четыре связанных компонента можно классифицировать по двум свойствам преобразования, которыми обладают их элементы:
- Некоторые элементы меняются местами при инвертирующих время преобразованиях Лоренца, например, указывающий на будущее вектор времени будет инвертирован в указывающий на прошлое вектор.
- Некоторые элементы имеют обратную ориентацию из-за неправильных преобразований Лоренца , например, некоторые вирбейны (тетрады)
Преобразования Лоренца, сохраняющие направление времени, называютсяортохронный . Подгруппа ортохронных преобразований часто обозначаетсяO + (1, 3). Те, которые сохраняют ориентацию, называютсясобственными, и как линейные преобразования они имеют определитель+1. (Несобственные преобразования Лоренца имеют определитель−1.) Подгруппа собственных преобразований Лоренца обозначаетсяSO(1, 3).
Подгруппа всех преобразований Лоренца, сохраняющая как ориентацию, так и направление времени, называется собственной ортохронной группой Лоренца или ограниченной группой Лоренца и обозначается SO + (1, 3) . [a]
Множество из четырех связных компонент может быть задано групповой структурой как факторгруппа O (1, 3) / SO + (1, 3) , которая изоморфна четверной группе Клейна . Каждый элемент в O(1, 3) может быть записан как полупрямое произведение собственного ортохронного преобразования и элемента дискретной группы
- {1, П , Т , ПТ }
где P и T — операторы четности и обращения времени :
- P = диагональ(1, −1, −1, −1)
- T = диаг(−1, 1, 1, 1) .
Таким образом, произвольное преобразование Лоренца может быть определено как правильное, ортохронное преобразование Лоренца вместе с двумя дополнительными битами информации, которые выбирают один из четырех связанных компонентов. Эта модель типична для конечномерных групп Ли.
Ограниченная группа Лоренца
Ограниченная группа Лоренца SO + (1, 3) является компонентом тождества группы Лоренца, что означает, что она состоит из всех преобразований Лоренца, которые могут быть связаны с тождеством непрерывной кривой, лежащей в группе. Ограниченная группа Лоренца является связной нормальной подгруппой полной группы Лоренца с той же размерностью, в данном случае с размерностью шесть.
Ограниченная группа Лоренца генерируется обычными пространственными вращениями и усилениями Лоренца (которые являются вращениями в гиперболическом пространстве, включающем времяподобное направление [2] ). Поскольку каждое собственное ортохронное преобразование Лоренца может быть записано как произведение вращения (задаваемого 3 действительными параметрами ) и усиления (также задаваемого 3 действительными параметрами), требуется 6 действительных параметров, чтобы задать произвольное собственное ортохронное преобразование Лоренца. Это один из способов понять, почему ограниченная группа Лоренца является шестимерной. (См. также алгебру Ли группы Лоренца.)
Множество всех вращений образует подгруппу Ли, изоморфную обычной группе вращений SO(3) . Однако множество всех усилений не образует подгруппу, поскольку составление двух усилений, как правило, не приводит к другому усилению. (Вместо этого пара неколлинеарных усилений эквивалентна усилению и вращению, и это относится к вращению Томаса .) Усиление в некотором направлении или вращение вокруг некоторой оси порождает однопараметрическую подгруппу .
Поверхности транзитивности
Если группа G действует на пространстве V , то поверхность S ⊂ V является поверхностью транзитивности , если S инвариантна относительно G (т. е. ∀ g ∈ G , ∀ s ∈ S : gs ∈ S ) и для любых двух точек s 1 , s 2 ∈ S существует g ∈ G такой, что gs 1 = s 2 . По определению группы Лоренца она сохраняет квадратичную форму
Поверхности транзитивности ортохронной группы Лоренца O + (1, 3) , Q ( x ) = const., действующей на плоском пространстве-времени R 1,3 , следующие: [3]
- Q ( x ) > 0, x 0 > 0 — верхняя ветвь двуполостного гиперболоида . Точки на этом листе отделены от начала координат будущим времяподобным вектором.
- Q ( x ) > 0, x 0 < 0 — нижняя ветвь этого гиперболоида. Точки на этом листе — прошлые времениподобные векторы.
- Q ( x ) = 0, x 0 > 0 — верхняя ветвь светового конуса , будущий световой конус.
- Q ( x ) = 0, x 0 < 0 — нижняя ветвь светового конуса, световой конус прошлого.
- Q ( x ) < 0 — однополостный гиперболоид. Точки на этом листе пространственно-подобны и отделены от начала координат.
- Начало координат x 0 = x 1 = x 2 = x 3 = 0 .
Эти поверхности являются 3 -мерными , поэтому изображения не являются точными, но они являются точными для соответствующих фактов о O + (1, 2) . Для полной группы Лоренца поверхностей транзитивности всего четыре, поскольку преобразование T переводит верхнюю ветвь гиперболоида (конуса) в нижнюю и наоборот.
Как симметричные пространства
Эквивалентный способ сформулировать вышеуказанные поверхности транзитивности — это симметричное пространство в смысле теории Ли. Например, верхний лист гиперболоида может быть записан как фактор-пространство SO + (1, 3) / SO(3) , благодаря теореме о стабилизаторе орбиты . Более того, этот верхний лист также предоставляет модель для трехмерного гиперболического пространства .
Представления группы Лоренца
Эти наблюдения представляют собой хорошую отправную точку для нахождения всех бесконечномерных унитарных представлений группы Лоренца, фактически, группы Пуанкаре, с использованием метода индуцированных представлений . [4] Начинаем со «стандартного вектора», по одному для каждой поверхности транзитивности, а затем спрашиваем, какая подгруппа сохраняет эти векторы. Эти подгруппы физики называют малыми группами . Затем проблема по существу сводится к более простой задаче нахождения представлений малых групп. Например, стандартный вектор в одной из гипербол двух листов может быть подходящим образом выбран как ( m , 0, 0, 0) . Для каждого m ≠ 0 вектор пронзает ровно один лист. В этом случае малая группа — это SO(3) , группа вращений , все представления которой известны. Точное бесконечномерное унитарное представление, при котором преобразуется частица, является частью ее классификации. Не все представления могут соответствовать физическим частицам (насколько известно). Стандартные векторы на однополостных гиперболах соответствовали бы тахионам . Частицы на световом конусе — это фотоны , а более гипотетически — гравитоны . «Частица», соответствующая началу координат, — это вакуум.
Гомоморфизмы и изоморфизмы
| Algebraic structure → Group theory Group theory |
|---|
 |
Несколько других групп либо гомоморфны, либо изоморфны ограниченной группе Лоренца SO + (1, 3) . Эти гомоморфизмы играют ключевую роль в объяснении различных явлений в физике.
- Специальная линейная группа SL(2, C ) является двойным покрытием ограниченной группы Лоренца. Это соотношение широко используется для выражения лоренц-инвариантности уравнения Дирака и ковариантности спиноров. Другими словами, (ограниченная) группа Лоренца изоморфна SL(2, C ) / Z 2
- Симплектическая группа Sp(2, C ) изоморфна SL(2, C ) ; она используется для построения спиноров Вейля , а также для объяснения того, как спиноры могут иметь массу.
- Группа спинов Spin(1, 3) изоморфна SL(2, C ) ; она используется для объяснения спина и спиноров в терминах алгебры Клиффорда , тем самым проясняя, как обобщить группу Лоренца на общие положения в римановой геометрии , включая теории супергравитации и теории струн .
- Ограниченная группа Лоренца изоморфна проективной специальной линейной группе PSL(2, C ), которая, в свою очередь, изоморфна группе Мёбиуса , группе симметрии конформной геометрии на сфере Римана . Это соотношение является центральным для классификации подгрупп группы Лоренца в соответствии с более ранней схемой классификации, разработанной для группы Мёбиуса.
представление Вейля
Представление Вейля или спинорное отображение — это пара сюръективных гомоморфизмов из SL(2, C ) в SO + (1, 3) . Они образуют согласованную пару при преобразованиях четности, соответствующих левым и правым хиральным спинорам.
Можно определить действие SL(2, C ) в пространстве-времени Минковского, записав точку пространства-времени как эрмитову матрицу размером два на два в форме
в терминах матриц Паули .
Это представление, представление Вейля, удовлетворяет
Таким образом, мы отождествили пространство эрмитовых матриц (которое является четырехмерным, как действительное векторное пространство) с пространством-временем Минковского таким образом, что определитель эрмитовой матрицы является квадратом длины соответствующего вектора в пространстве-времени Минковского. Элемент S ∈ SL(2, C ) действует на пространстве эрмитовых матриц посредством
где — эрмитово транспонирование S . Это действие сохраняет определитель, и поэтому SL(2, C ) действует на пространстве-времени Минковского посредством (линейных) изометрий. Форма выше с инвертированной четностью —
который преобразуется как
То, что это правильное преобразование, следует из того, что
остается инвариантным относительно указанной выше пары преобразований.
Эти отображения сюръективны , и ядром любого отображения является двухэлементная подгруппа ± I. По первой теореме об изоморфизме фактор-группа PSL(2, C ) = SL(2, C ) / {± I } изоморфна SO + (1, 3) .
Отображение четности меняет местами эти два покрытия. Оно соответствует эрмитовому сопряжению, являющемуся автоморфизмом SL(2, C ) . Эти два различных покрытия соответствуют двум различным хиральным действиям группы Лоренца на спинорах . Неперечеркнутая форма соответствует правосторонним спинорам, преобразующимся как , в то время как перечеркнутая форма соответствует левосторонним спинорам, преобразующимся как . [b]
Важно отметить, что эта пара покрытий не выдерживает квантования; при квантовании это приводит к своеобразному явлению хиральной аномалии . Классические (т.е. неквантованные) симметрии группы Лоренца нарушаются квантованием; это содержание теоремы Атьи–Зингера об индексе .
Условные обозначения
В физике принято обозначать преобразование Лоренца Λ ∈ SO + (1, 3) как , тем самым показывая матрицу с индексами пространства-времени μ , ν = 0, 1, 2, 3 . Четырехвектор может быть создан из матриц Паули двумя различными способами: как и как . Две формы связаны преобразованием четности . Обратите внимание, что .
Учитывая преобразование Лоренца , двойное накрытие ортохронной группы Лоренца посредством S ∈ SL(2, C ), заданное выше, можно записать как
Отбрасывая это принимает форму
Сопряженная по четности форма:
Доказательство
То, что вышеприведенная форма является правильной для индексированной записи, не очевидно сразу, отчасти потому, что при работе в индексированной записи довольно легко случайно спутать преобразование Лоренца с его обратным или транспонированным. Эта путаница возникает из-за того, что тождество трудно распознать, когда оно записано в индексированной форме. Преобразования Лоренца не являются тензорами относительно преобразований Лоренца! Таким образом, прямое доказательство этого тождества полезно для установления его правильности. Его можно продемонстрировать, начав с тождества
где так что выше просто обычные матрицы Паули, и является транспонированной матрицей, и является комплексным сопряжением. Матрица
Записанная в виде четырехвектора, эта связь имеет вид
Это преобразуется как
Сделав еще одну транспозицию, получаем
Симплектическая группа
Симплектическая группа Sp(2, C ) изоморфна SL(2, C ) . Этот изоморфизм построен так, чтобы сохранить симплектическую билинейную форму на C 2 , то есть оставить форму инвариантной относительно преобразований Лоренца. Это можно сформулировать следующим образом. Симплектическая группа определяется как
где
Для этого элемента используются и другие общепринятые обозначения ; иногда используется J , но это вызывает путаницу с идеей почти сложных структур , которые не являются одним и тем же, поскольку они трансформируются по-разному.
Дана пара спиноров Вейля (двухкомпонентные спиноры)
инвариантная билинейная форма обычно записывается как
Эта форма инвариантна относительно группы Лоренца, так что для S ∈ SL(2, C ) имеем
Это определяет своего рода «скалярное произведение» спиноров и обычно используется для определения лоренц-инвариантного массового члена в лагранжианах . Следует назвать несколько примечательных свойств, которые важны для физики. Одно из них заключается в том, что и так
Определяющее соотношение можно записать как
что очень похоже на определяющее соотношение для группы Лоренца
где — метрический тензор для пространства Минковского и, конечно, как и прежде.
Группы покрытия
Так как SL(2, C ) односвязна, то она является универсальной накрывающей группой ограниченной группы Лоренца SO + (1, 3) . По ограничению существует гомоморфизм SU(2) → SO(3) . Здесь специальная унитарная группа SU(2), которая изоморфна группе кватернионов единичной нормы , также односвязна, поэтому она является накрывающей группой группы вращений SO(3) . Каждое из этих накрывающих отображений является двукратным накрытием в том смысле, что ровно два элемента накрывающей группы отображаются в каждый элемент фактора. Часто говорят, что ограниченная группа Лоренца и группа вращений двусвязны . Это означает, что фундаментальная группа каждой группы изоморфна двухэлементной циклической группе Z 2 .
Двукратные покрытия характерны для спиновых групп . Действительно, в дополнение к двукратным покрытиям
- Спин + (1, 3) = SL(2, C ) → SO + (1, 3)
- Спин(3) = SU(2) → SO(3)
у нас есть двойные покрытия
- Пин(1, 3) → О(1, 3)
- Спин(1, 3) → SO(1, 3)
- Спин + (1, 2) = SU(1, 1) → SO(1, 2)
Эти спинорные двойные покрытия строятся на основе алгебр Клиффорда .
Топология
Левая и правая группы в двойном покрытии
- СУ(2) → СО(3)
являются деформационными ретрактами левой и правой групп соответственно в двойном покрытии
- SL(2, C ) → SO + (1, 3) .
Но однородное пространство SO + (1, 3) / SO(3) гомеоморфно гиперболическому 3-пространству H 3 , поэтому мы представили ограниченную группу Лоренца как главное расслоение со слоями SO (3) и базой H 3 . Поскольку последняя гомеоморфна R 3 , в то время как SO(3) гомеоморфна трехмерному действительному проективному пространству R P 3 , мы видим, что ограниченная группа Лоренца локально гомеоморфна произведению R P 3 на R 3 . Поскольку базовое пространство стягиваемо, это можно расширить до глобального гомеоморфизма. [ необходимо разъяснение ]
Классы сопряженности
Поскольку ограниченная группа Лоренца SO + (1, 3) изоморфна группе Мёбиуса PSL(2, C ) , ее классы сопряженности также делятся на пять классов:
- Эллиптические преобразования
- Гиперболические преобразования
- Локсодромные преобразования
- Параболические преобразования
- Тривиальное преобразование идентичности
В статье о преобразованиях Мёбиуса объясняется, как возникает эта классификация путем рассмотрения неподвижных точек преобразований Мёбиуса в их действии на сфере Римана, что соответствует здесь нулевым собственным подпространствам ограниченных преобразований Лоренца в их действии на пространстве-времени Минковского.
Пример каждого типа приведен в подразделах ниже, вместе с эффектом однопараметрической подгруппы, которую он генерирует (например, на внешний вид ночного неба).
Преобразования Мёбиуса являются конформными преобразованиями сферы Римана (или небесной сферы). Затем сопряжение с произвольным элементом SL(2, C ) дает следующие примеры произвольных эллиптических, гиперболических, локсодромических и параболических (ограниченных) преобразований Лоренца соответственно. Эффект на линии потока соответствующих однопараметрических подгрупп заключается в преобразовании рисунка, видимого в примерах, некоторым конформным преобразованием. Например, эллиптическое преобразование Лоренца может иметь любые две различные неподвижные точки на небесной сфере, но точки по-прежнему текут по дугам окружностей от одной неподвижной точки к другой. Другие случаи аналогичны.
Эллиптический
Эллиптический элемент SL(2, C ) — это
и имеет неподвижные точки ξ = 0, ∞. Записывая действие как X ↦ P 1 X P 1 † и собирая члены, спинорное отображение преобразует это в (ограниченное) преобразование Лоренца
Это преобразование затем представляет собой вращение вокруг оси z , exp( iθJ z ). Однопараметрическая подгруппа, которую оно генерирует, получается, если взять θ в качестве действительной переменной, угла поворота, вместо константы.
Соответствующие непрерывные преобразования небесной сферы (за исключением тождества) все разделяют те же две фиксированные точки, Северный и Южный полюса. Преобразования перемещают все остальные точки по кругам широты так, что эта группа дает непрерывное вращение против часовой стрелки вокруг оси z по мере увеличения θ . Удвоение угла, очевидное в карте спинора, является характерной чертой спинорных двойных покрытий .
Гиперболический
Гиперболический элемент SL(2, C ) — это
и имеет неподвижные точки ξ = 0, ∞. При стереографической проекции со сферы Римана на евклидову плоскость эффект этого преобразования Мёбиуса представляет собой растяжение от начала координат.
Спинорная карта преобразует это в преобразование Лоренца
Это преобразование представляет собой ускорение вдоль оси z с быстротой η . Однопараметрическая подгруппа, которую оно генерирует, получается, если взять η как действительную переменную, а не константу. Соответствующие непрерывные преобразования небесной сферы (за исключением тождества) все имеют одни и те же фиксированные точки (Северный и Южный полюса), и они перемещают все остальные точки вдоль долгот от Южного полюса к Северному полюсу.
Локсодромный
Локсодромный элемент SL(2, C ) — это
и имеет фиксированные точки ξ = 0, ∞. Спинорное отображение преобразует это в преобразование Лоренца
Однопараметрическая подгруппа, которую это генерирует, получается путем замены η + i θ на любое действительное кратное этой комплексной константы. (Если η , θ изменяются независимо, то получается двумерная абелева подгруппа , состоящая из одновременных вращений вокруг оси z и ускорений вдоль оси z ; в отличие от этого, одномерная подгруппа, обсуждаемая здесь, состоит из тех элементов этой двумерной подгруппы, что скорость ускорения и угол вращения имеют фиксированное отношение .)
Соответствующие непрерывные преобразования небесной сферы (за исключением тождества) все имеют одни и те же две фиксированные точки (Северный и Южный полюса). Они перемещают все остальные точки от Южного полюса к Северному полюсу (или наоборот) вдоль семейства кривых, называемых локсодромами . Каждая локсодромия бесконечно часто закручивается по спирали вокруг каждого полюса.
Параболический
Параболический элемент SL(2, C ) — это
и имеет единственную неподвижную точку ξ = ∞ на сфере Римана. При стереографической проекции она выглядит как обычный перенос вдоль действительной оси .
Спинорная карта преобразует это в матрицу (представляющую собой преобразование Лоренца)
Это порождает двухпараметрическую абелеву подгруппу, которая получается, если рассматривать α как комплексную переменную, а не как константу. Соответствующие непрерывные преобразования небесной сферы (за исключением тождественного преобразования) перемещают точки по семейству окружностей, которые все касаются в Северном полюсе некоторой большой окружности . Все точки, кроме самого Северного полюса, перемещаются по этим окружностям.
Параболические преобразования Лоренца часто называют нулевыми вращениями . Поскольку они, вероятно, являются наименее известными из четырех типов нетождественных преобразований Лоренца (эллиптическое, гиперболическое, локсодромическое, параболическое), здесь показано, как определить влияние примера параболического преобразования Лоренца на пространство-время Минковского.
Приведенная выше матрица дает преобразование
Теперь, не теряя общности, выберем Im( α ) = 0. Дифференцирование этого преобразования по теперь действительному групповому параметру α и оценка при α = 0 дает соответствующее векторное поле (линейный частный дифференциальный оператор первого порядка),
Применим это к функции f ( t , x , y , z ) и потребуем, чтобы она оставалась инвариантной; т. е. уничтожалась этим преобразованием. Решение полученного линейного уравнения в частных производных первого порядка можно выразить в виде
где F — произвольная гладкая функция. Аргументы F дают три рациональных инварианта, описывающих, как точки (события) движутся при этом параболическом преобразовании, поскольку сами они не движутся,
Выбор действительных значений для констант в правых частях дает три условия и, таким образом, задает кривую в пространстве-времени Минковского. Эта кривая является орбитой преобразования.
Форма рациональных инвариантов показывает, что эти линии тока (орбиты) имеют простое описание: опуская несущественную координату y , каждая орбита является пересечением нулевой плоскости , t = z + c 2 , с гиперболоидом , t 2 − x 2 − z 2 = c 3 . Случай c 3 = 0 имеет гиперболоид, вырожденный в световой конус, причем орбиты становятся параболами, лежащими в соответствующих нулевых плоскостях.
Конкретная нулевая линия, лежащая на световом конусе, остается инвариантной ; это соответствует единственной (двойной) неподвижной точке на сфере Римана, упомянутой выше. Другие нулевые линии, проходящие через начало координат, «разворачиваются вокруг конуса» преобразованием. Отслеживание движения одной такой нулевой линии по мере увеличения α соответствует отслеживанию движения точки вдоль одной из круговых линий потока на небесной сфере, как описано выше.
Выбор Re( α ) = 0 вместо этого приводит к получению похожих орбит, но теперь роли x и y меняются местами.
Параболические преобразования приводят к калибровочной симметрии безмассовых частиц (таких как фотоны ) со спиральностью | h | ≥ 1. В приведенном выше явном примере безмассовая частица, движущаяся в направлении z , то есть с 4-импульсом P = ( p , 0, 0, p ) , вообще не подвержена влиянию комбинации x -усиления и y -вращения K x − J y , определенной ниже, в «малой группе» ее движения. Это очевидно из обсуждаемого явного закона преобразования: как и любой светоподобный вектор, сам P теперь инвариантен; т. е. все следы или эффекты α исчезли. c 1 = c 2 = c 3 = 0 , в обсуждаемом особом случае. (Другой аналогичный генератор, K y + J x , а также он и J z составляют в целом малую группу светоподобного вектора, изоморфную E (2) .)
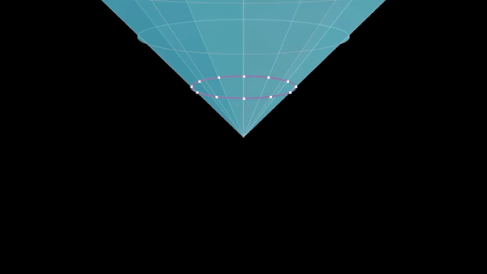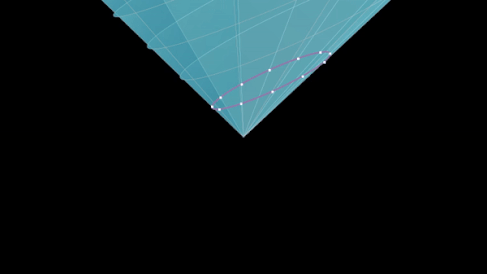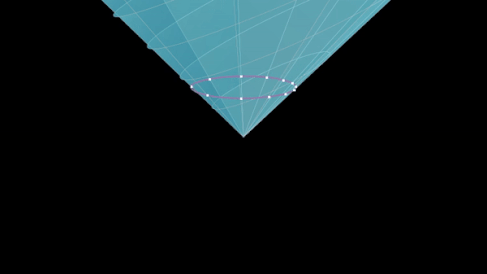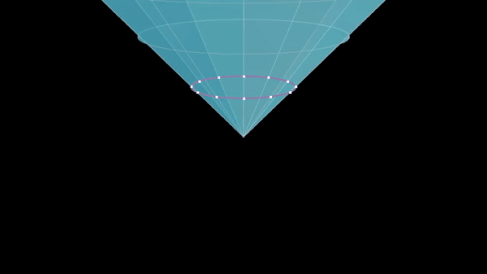
Вид ночного неба
Этот изоморфизм приводит к тому, что преобразования Мёбиуса сферы Римана отражают способ, которым преобразования Лоренца изменяют вид ночного неба, видимого наблюдателем, который движется с релятивистской скоростью относительно «неподвижных звезд».
Предположим, что «неподвижные звезды» живут в пространстве-времени Минковского и моделируются точками на небесной сфере. Тогда заданная точка на небесной сфере может быть связана с ξ = u + iv , комплексным числом, которое соответствует точке на сфере Римана , и может быть идентифицирована с нулевым вектором ( светоподобным вектором ) в пространстве Минковского
или, в представлении Вейля (спинорное отображение), эрмитова матрица

Набор действительных скалярных кратных этого нулевого вектора, называемый нулевой линией через начало координат, представляет собой линию визирования от наблюдателя в определенном месте и времени (произвольное событие, которое мы можем отождествить с началом пространства-времени Минковского) к различным удаленным объектам, таким как звезды. Затем точки небесной сферы (эквивалентно линии визирования) отождествляются с определенными эрмитовыми матрицами.
Проективная геометрия и различные виды 2-сферы
Эта картина возникает чисто на языке проективной геометрии. (Ограниченная) группа Лоренца действует на проективную небесную сферу . Это пространство ненулевых нулевых векторов с под заданным частным для проективных пространств: если для . Это называется небесной сферой, поскольку это позволяет нам перемасштабировать временную координату до 1 после действия с использованием преобразования Лоренца, гарантируя, что пространственно-подобная часть находится на единичной сфере.
Со стороны Мёбиуса SL(2, C ) действует на комплексное проективное пространство C P 1 , которое, как можно показать, диффеоморфно 2-сфере – ее иногда называют сферой Римана. Фактор по проективному пространству приводит к фактору по группе SL(2, C ) .
Наконец, эти два вектора можно связать вместе, используя комплексный проективный вектор для построения нулевого вектора. Если — проективный вектор C P 1 , его можно тензорно умножить на его эрмитово сопряженный вектор, чтобы получить эрмитову матрицу. Из других мест в этой статье мы знаем, что это пространство матриц можно рассматривать как 4-векторы. Пространство матриц, получаемое путем превращения каждого проективного вектора в сфере Римана в матрицу, известно как сфера Блоха .
алгебра Ли
| Lie groups and Lie algebras |
|---|
 |
Как и в случае с любой группой Ли, полезным способом изучения многих аспектов группы Лоренца является ее алгебра Ли . Поскольку группа Лоренца SO(1, 3) является матричной группой Ли , ее соответствующая алгебра Ли является матричной алгеброй Ли, которая может быть вычислена как [5]
- .
Если — диагональная матрица с диагональными элементами (1, −1, −1, −1) , то алгебра Ли состоит из матриц таких, что [6]
- .
Явно состоит из матриц вида
- ,
где — произвольные действительные числа. Эта алгебра Ли шестимерна. Подалгебра , состоящая из элементов, в которых , , и равны нулю, изоморфна .
Полная группа Лоренца O(1, 3) , собственная группа Лоренца SO(1, 3) и собственная ортохронная группа Лоренца SO + (1, 3) (компонента, связанная с единицей) имеют одну и ту же алгебру Ли, которая обычно обозначается .
Поскольку единичный компонент группы Лоренца изоморфен конечному фактору SL(2, C ) (см. раздел выше о связи группы Лоренца с группой Мёбиуса), алгебра Ли группы Лоренца изоморфна алгебре Ли . Как комплексная алгебра Ли является трехмерной, но является шестимерной, если рассматривать ее как действительную алгебру Ли.
Коммутационные соотношения алгебры Лоренца
Стандартные базисные матрицы могут быть проиндексированы как , где принимают значения в {0, 1, 2, 3} . Они возникают из-за того, что только один из них принимается равным единице, а другие равны нулю, в свою очередь. Компоненты могут быть записаны как
- .
Коммутационные соотношения следующие:
Существуют различные возможные варианты используемых соглашений. В физике принято включать фактор с базисными элементами, что дает фактор в коммутационных соотношениях.
Затем сгенерируйте усиления и вращения.
Структурные константы для алгебры Лоренца можно вывести из коммутационных соотношений. Любой набор базисных элементов, удовлетворяющих этим соотношениям, образует представление алгебры Лоренца.
Генераторы ускорений и вращений
Группа Лоренца может рассматриваться как подгруппа группы диффеоморфизмов R 4 , и поэтому ее алгебра Ли может быть отождествлена с векторными полями на R 4 . В частности, векторы, которые генерируют изометрии на пространстве, являются его векторами Киллинга , что обеспечивает удобную альтернативу левоинвариантному векторному полю для вычисления алгебры Ли. Мы можем записать набор из шести генераторов :
- Векторные поля на R 4 , генерирующие три вращения i J ,
- Векторные поля на R 4 генерируют три усиления i K ,
Множитель i , по-видимому, гарантирует, что генераторы вращений являются эрмитовыми.
Здесь может быть полезно кратко напомнить, как получить однопараметрическую группу из векторного поля , записанного в форме линейного частного дифференциального оператора первого порядка , например,
Соответствующая задача начального значения (рассмотрим функцию скаляра и решим ее с некоторыми начальными условиями) имеет вид
Решение можно записать
или
где мы легко распознаем однопараметрическую матричную группу вращений exp( iλJ z ) вокруг оси z.
Дифференцируя по групповому параметру λ и устанавливая в этом результате λ = 0 , мы восстанавливаем стандартную матрицу,
что соответствует векторному полю, с которого мы начали. Это иллюстрирует, как переходить между матричными и векторными представлениями элементов алгебры Ли. Экспоненциальное отображение играет эту особую роль не только для группы Лоренца, но и для групп Ли в целом.
Обращая процедуру, описанную в предыдущем разделе, мы видим, что преобразования Мёбиуса, соответствующие нашим шести генераторам, возникают из возведения в степень соответственно η /2 (для трех усилений) или iθ /2 (для трех вращений) трех матриц Паули .
Генераторы группы Мёбиуса
Другой набор генераторов возникает через изоморфизм к группе Мёбиуса. В следующей таблице перечислены шесть генераторов, в которых
- В первом столбце приведен генератор потока под действием Мёбиуса (после стереографической проекции со сферы Римана) как действительного векторного поля на евклидовой плоскости.
- Во втором столбце дана соответствующая однопараметрическая подгруппа преобразований Мёбиуса.
- В третьем столбце указана соответствующая однопараметрическая подгруппа преобразований Лоренца (образ при нашем гомоморфизме предыдущей однопараметрической подгруппы).
- В четвертом столбце приведен соответствующий генератор потока под действием Лоренца как действительное векторное поле в пространстве-времени Минковского.
Обратите внимание, что генераторы состоят из
- Две параболы (нулевые вращения)
- Один гиперболический (усиление в направлении)
- Три эллипса (вращение вокруг осей x , y , z соответственно)
| Вектор поля на R 2 | Однопараметрическая подгруппа SL(2, C ) , представляющая преобразования Мёбиуса | Однопараметрическая подгруппа SO + (1, 3) , представляющая преобразования Лоренца | Вектор поля на R 1,3 |
|---|---|---|---|
| Параболический | |||
| Гиперболический | |||
| Эллиптический | |||
Рабочий пример: вращение вокруг оси Y
Начать с
Возвести в степень:
Этот элемент SL(2, C ) представляет собой однопараметрическую подгруппу (эллиптических) преобразований Мёбиуса:
Следующий,
Соответствующее векторное поле на C (рассматриваемое как изображение S2 при стереографической проекции) равно
Записывая , это становится векторным полем на R 2
Возвращаясь к нашему элементу SL(2, C ) , записывая действие и собирая члены, мы обнаруживаем, что изображение под спинорным отображением является элементом SO + (1, 3)
Дифференцируя по θ при θ = 0 , получаем соответствующее векторное поле на R 1,3 ,
Очевидно, это генератор вращения против часовой стрелки вокруг оси Y.
Подгруппы группы Лоренца
Подалгебры алгебры Ли группы Лоренца можно перечислить с точностью до сопряженности, из которых можно вывести замкнутые подгруппы ограниченной группы Лоренца с точностью до сопряженности. (Подробности см. в книге Холла, цитируемой ниже.) Их можно легко выразить через генераторы, указанные в таблице выше.
Одномерные подалгебры, конечно, соответствуют четырем классам сопряженности элементов группы Лоренца:
- генерирует однопараметрическую подалгебру параболиков SO(0, 1) ,
- генерирует однопараметрическую подалгебру улучшений SO(1, 1) ,
- генерирует однопараметрический поворот SO(2) ,
- (для любого ) порождает однопараметрическую подалгебру локсодромических преобразований.
(Строго говоря, последнее соответствует бесконечному числу классов, поскольку различные дают разные классы.) Двумерные подалгебры:
- генерирует абелеву подалгебру, состоящую исключительно из параболиков,
- порождают неабелеву подалгебру, изоморфную алгебре Ли аффинной группы Aff(1) ,
- генерируют абелеву подалгебру, состоящую из бустов, вращений и локсодромий, имеющих одну и ту же пару неподвижных точек.
Трехмерные подалгебры используют схему классификации Бианки :
- порождают подалгебру Бьянки V , изоморфную алгебре Ли Hom(2) , группе евклидовых гомотетий ,
- порождают подалгебру Бьянки VII 0 , изоморфную алгебре Ли E (2) , евклидовой группе ,
- , где , порождают подалгебру Бьянки VII ,
- порождают подалгебру Бьянки VIII , изоморфную алгебре Ли SL(2, R ) , группе изометрий гиперболической плоскости ,
- генерируют подалгебру Бьянки IX , изоморфную алгебре Ли SO(3) , группе вращений.
Типы Бьянки относятся к классификации трехмерных алгебр Ли итальянского математика Луиджи Бьянки .
Четырехмерные подалгебры все сопряжены
- порождают подалгебру, изоморфную алгебре Ли Sim(2) , группе евклидовых подобий .
Подалгебры образуют решетку (см. рисунок), и каждая подалгебра порождает путем возведения в степень замкнутую подгруппу ограниченной группы Ли. Из них можно построить все подгруппы группы Лоренца с точностью до сопряжения путем умножения на один из элементов четверной группы Клейна.

Как и в случае любой связной группы Ли, пространства смежных классов замкнутых подгрупп ограниченной группы Лоренца, или однородные пространства , представляют значительный математический интерес. Несколько кратких описаний:
- Группа Sim(2) является стабилизатором нулевой линии , т. е. точки на сфере Римана, поэтому однородное пространство SO + (1, 3) / Sim(2) является геометрией Клейна , которая представляет конформную геометрию на сфере S 2 .
- (Единичный компонент) евклидовой группы SE(2) является стабилизатором нулевого вектора , поэтому однородное пространство SO + (1, 3) / SE(2) является импульсным пространством безмассовой частицы; геометрически эта клейнова геометрия представляет собой вырожденную геометрию светового конуса в пространстве-времени Минковского.
- Группа вращений SO(3) является стабилизатором времениподобного вектора , поэтому однородное пространство SO + (1, 3) / SO(3) является импульсным пространством массивной частицы; геометрически это пространство есть не что иное, как трехмерное гиперболическое пространство H 3 .
Обобщение на более высокие измерения
Концепция группы Лоренца имеет естественное обобщение на пространство-время любого числа измерений. Математически группа Лоренца ( n + 1)-мерного пространства Минковского является неопределенной ортогональной группой O( n , 1) линейных преобразований Rn + 1 , которая сохраняет квадратичную форму
Группа O(1, n ) сохраняет квадратичную форму
O(1, n ) изоморфна O( n , 1) , и обе формы представления группы Лоренца используются в сообществе теоретической физики. Первая форма более распространена в литературе, связанной с гравитацией, тогда как вторая форма более распространена в литературе по физике элементарных частиц.
Распространенное обозначение для векторного пространства R n +1 , снабженного этим выбором квадратичной формы, — R 1, n .
Многие свойства группы Лоренца в четырех измерениях (где n = 3 ) напрямую обобщаются на произвольные n . Например, группа Лоренца O( n , 1) имеет четыре связные компоненты и действует конформными преобразованиями на небесной ( n − 1) -сфере в ( n + 1) -мерном пространстве Минковского. Компонент тождества SO + ( n , 1) является SO( n ) -расслоением над гиперболическим n -пространством H n .
Низкоразмерные случаи n = 1 и n = 2 часто полезны в качестве «игрушечных моделей» для физического случая n = 3 , в то время как группы Лоренца более высокой размерности используются в физических теориях, таких как теория струн , которые постулируют существование скрытых измерений. Группа Лоренца O( n , 1) также является группой изометрий n -мерного пространства де Ситтера dS n , которое может быть реализовано как однородное пространство O( n , 1) / O( n − 1, 1) . В частности, O(4, 1) является группой изометрий вселенной де Ситтера dS 4 , космологической модели.
Смотрите также
Примечания
- ^ Обратите внимание, что некоторые авторы ссылаются на SO(1, 3) или даже O(1, 3), когда имеют в виду SO + (1, 3) .
- ^ См. статью Уравнение Вейля для явных выводов.
Ссылки
- ^ Вайнберг 2002
- ^ Варичак В 1910 "Теория относительности и геометрия Лобачевского", Phys Z 1910 §3 "Преобразование Лоренца-Эйнштейна как перевод". Engl.tr в Википедии
- ^ Гельфанд, Минлос и Шапиро 1963
- ^ Вигнер 1939
- ^ Холл 2015 Определение 3.18
- ^ Холл 2015 Предложение 3.25
Список для чтения
- Эмиль Артин (1957) Геометрическая алгебра, глава III: Симплектическая и ортогональная геометрия через интернет-архив , охватывает ортогональные группы O( p , q )
- Кармели, Моше (1977). Теория групп и общая теория относительности, представления группы Лоренца и их приложения к гравитационному полю . McGraw-Hill, Нью-Йорк. ISBN 978-0-07-009986-9.Каноническая ссылка; см. главы 1–6 для ознакомления с представлениями группы Лоренца.
- Франкель, Теодор (2004). Геометрия физики (2-е изд.) . Кембридж: Cambridge University Press. ISBN 978-0-521-53927-2. Превосходный ресурс по теории Ли, расслоениям волокон, спинорным покрытиям и многим другим темам.
- Фултон, Уильям ; Харрис, Джо (1991). Теория представлений. Первый курс . Graduate Texts in Mathematics , Readings in Mathematics. Том 129. Нью-Йорк: Springer-Verlag. doi :10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103. См. лекцию 11 о неприводимых представлениях SL(2, C ) .
- Гельфанд, И.М.; Минлос , Р.А .; Шапиро, З.Я. (1963), Представления групп вращения и Лоренца и их приложения , Нью-Йорк: Pergamon Press
- Холл, Брайан С. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Graduate Texts in Mathematics, т. 222 (2-е изд.), Springer, ISBN 978-3319134666
- Холл, Г.С. (2004). Симметрии и структура кривизны в общей теории относительности . Сингапур: World Scientific. ISBN 978-981-02-1051-9. Подалгебры алгебры Ли группы Лоренца см. в главе 6 .
- Хэтчер, Аллен (2002). Алгебраическая топология . Кембридж: Cambridge University Press. ISBN 978-0-521-79540-1. См. также "онлайн-версию" . Получено 3 июля 2005 г. См. Раздел 1.3 для прекрасно иллюстрированного обсуждения накрывающих пространств. См. Раздел 3D для топологии групп вращения.
- Мизнер, Чарльз ; Торн, Кип С.; Уиллер , Джон (1973). Гравитация . WH Freeman and Company . ISBN 978-0-7167-0344-0.§41.3
- Набер, Грегори (1992). Геометрия пространства-времени Минковского . Нью-Йорк: Springer-Verlag. ISBN 978-0486432359.(Переиздание Dover.) Превосходный справочник по пространству-времени Минковского и группе Лоренца.
- Needham, Tristan (1997). Визуальный комплексный анализ . Оксфорд: Oxford University Press. ISBN 978-0-19-853446-4. Превосходно иллюстрированное обсуждение преобразований Мёбиуса см. в Главе 3 .
- Вайнберг, С. (2002), Квантовая теория полей , т. 1, Cambridge University Press , ISBN 978-0-521-55001-7
- Вигнер, Э. П. (1939), «Об унитарных представлениях неоднородной группы Лоренца», Annals of Mathematics , 40 (1): 149– 204, Bibcode : 1939AnMat..40..149W, doi : 10.2307/1968551, JSTOR 1968551, MR 1503456, S2CID 121773411



















































![{\displaystyle {\begin{aligned}Q_{4}&={\begin{bmatrix}1+{\frac {1}{2}}\vert \alpha \vert ^{2}&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&-{\frac {1}{2}}\vert \alpha \vert ^{2}\\\operatorname {Re} (\alpha )&1&0&-\operatorname {Re} (\alpha )\\-\operatorname {Im} (\alpha )&0&1&\operatorname {Im} (\alpha )\\{\frac {1}{2}}\vert \alpha \vert ^{2}&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&1-{\frac {1}{2}}\vert \alpha \vert ^{2}\end{bmatrix}}\\[6pt]&=\exp {\begin{bmatrix}0&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&0\\\operatorname {Re} (\alpha )&0&0&-\operatorname {Re} (\alpha )\\-\operatorname {Im} (\alpha )&0&0&\operatorname {Im} (\alpha )\\0&\operatorname {Re} (\alpha )&-\operatorname {Im} (\alpha )&0\end{bmatrix}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fe74e84f87ed4999b00c40a37587136c1737f14)































![{\displaystyle [M^{\mu \nu },M^{\rho \sigma }]=M^{\mu \sigma }\eta ^{\nu \rho }-M^{\nu \sigma }\ эта ^{\му \rho }+M^{\nu \rho }\eta ^{\mu \sigma }-M^{\mu \rho }\eta ^{\nu \sigma }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94a9022837b52dcbbcf58bf59339dd5754657dfe)

































































