Группа контактов
В математике пин -группа — это определенная подгруппа алгебры Клиффорда , связанная с квадратичным пространством . Она отображает 2-в-1 в ортогональную группу , так же как спиновая группа отображает 2-в-1 в специальную ортогональную группу .
В общем случае отображение из группы Пина в ортогональную группу не является ни сюръективным , ни универсальным накрывающим пространством , но если квадратичная форма определена (и размерность больше 2), то оно является и тем, и другим.
Нетривиальный элемент ядра обозначается , что не следует путать с ортогональным преобразованием отражения через начало координат , обычно обозначаемым
Общее определение
Пусть будет векторным пространством с невырожденной квадратичной формой . Группа пинов — это подмножество алгебры Клиффорда, состоящее из элементов вида , где — векторы такие, что . Группа спинов определяется аналогично, но с ограничением на четность; она является подгруппой группы пинов. [1]
В этой статье всегда является действительным векторным пространством. Когда имеет базисные векторы, удовлетворяющие и группа контактов обозначается Pin( p , q ).
Геометрически для векторов с , является отражением вектора относительно гиперплоскости, ортогональной к . В более общем смысле, элемент группы штифтов действует на векторы, преобразуясь в , что является композицией k отражений. Поскольку каждое ортогональное преобразование может быть выражено как композиция отражений ( теорема Картана–Дьедонне ), отсюда следует, что это представление группы штифтов является гомоморфизмом из группы штифтов на ортогональную группу. Это часто называют скрученным присоединенным представлением. Элементы ±1 группы штифтов являются элементами, которые отображаются в тождество , и каждый элемент из соответствует ровно двум элементам из . [2]
Определенная форма
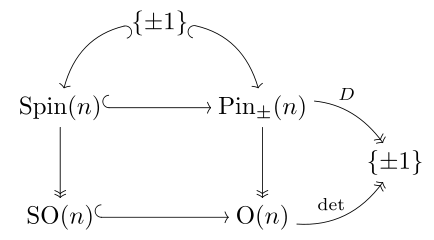
Группа выводов определенной формы отображается на ортогональную группу, и каждая компонента односвязна (в размерности 3 и выше): она дважды покрывает ортогональную группу. Группы выводов для положительно определенной квадратичной формы Q и для ее отрицательной − Q не изоморфны, но ортогональные группы изоморфны. [примечание 1]
В терминах стандартных форм O( n , 0) = O(0, n ), но Pin( n , 0) и Pin(0, n ) в общем случае не изоморфны. Используя соглашение о знаке "+" для алгебр Клиффорда (где ), можно записать
и оба они отображаются на O( n ) = O( n , 0) = O(0, n ).
Напротив, у нас есть естественный изоморфизм [примечание 2] Spin( n , 0) ≅ Spin(0, n ), и они оба являются (единственным) нетривиальным двойным покрытием специальной ортогональной группы SO( n ), которая является (единственным) универсальным покрытием для n ≥ 3.
Неопределенная форма
![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion. You can help by adding to it. (December 2009) |
Существует целых восемь различных двойных покрытий O( p , q ) для p , q ≠ 0, которые соответствуют расширениям центра (который является либо C 2 × C 2 , либо C 4 ) посредством C 2 . Только два из них являются группами контактов — теми, которые допускают алгебру Клиффорда в качестве представления. Они называются Pin( p , q ) и Pin( q , p ) соответственно.
Как топологическая группа
Каждая связная топологическая группа имеет единственное универсальное покрытие как топологическое пространство, которое имеет единственную групповую структуру как центральное расширение фундаментальной группы. Для несвязной топологической группы существует единственное универсальное покрытие компонента тождества группы, и можно взять то же покрытие как топологические пространства на других компонентах (которые являются главными однородными пространствами для компонента тождества), но групповая структура на других компонентах в общем случае не определена однозначно.
Группы Pin и Spin являются особыми топологическими группами, связанными с ортогональными и специальными ортогональными группами, происходящими из алгебр Клиффорда: существуют и другие подобные группы, соответствующие другим двойным покрытиям или другим групповым структурам на других компонентах, но они не называются группами Pin или Spin и не изучаются особо.
В 2001 году Анджей Траутман [примечание 3] нашел множество всех 32 неэквивалентных двойных накрытий O( p ) x O( q ), максимальную компактную подгруппу O( p , q ) и явную конструкцию 8 двойных накрытий той же группы O( p , q ).
Строительство
Две группы штифтов соответствуют двум центральным расширениям.
Групповая структура на Spin( V ) (связный компонент определителя 1) уже определена; групповая структура на другом компоненте определена вплоть до центра и, таким образом, имеет неоднозначность ±1.
Два расширения различаются тем, дает ли прообраз отражения квадрат ±1 ∈ Ker (Spin( V ) → SO( V )), и две группы контактов названы соответственно. Явно, отражение имеет порядок 2 в O( V ), r 2 = 1, поэтому квадрат прообраза отражения (который имеет определитель 1) должен быть в ядре Spin ± ( V ) → SO( V ), поэтому , и любой выбор определяет группу контактов (поскольку все отражения сопряжены элементом SO( V ), который связен, все отражения должны давать один и тот же квадрат).
Конкретно, в Pin + имеет порядок 2, а прообраз подгруппы {1, r } равен C 2 × C 2 : если повторить одно и то же отражение дважды, то получится тождество.
В Pin − имеет порядок 4, а прообразом подгруппы {1, r } является C 4 : если повторить одно и то же отражение дважды, то получится « поворот на 2π» — нетривиальный элемент Spin( V ) → SO( V ) можно интерпретировать как «поворот на 2π» (каждая ось дает один и тот же элемент).
Низкие габариты
В 1 измерении группы штифтов соответствуют первым диэдральным и дициклическим группам:
В 2 измерениях различие между Pin + и Pin − отражает различие между диэдральной группой 2 n -угольника и дициклической группой циклической группы C 2 n .
В Pin + прообразом диэдральной группы n -угольника, рассматриваемой как подгруппа Dih n < O(2), является диэдральная группа 2 n -угольника, Dih 2 n < Pin + (2), тогда как в Pin − прообразом диэдральной группы является дициклическая группа Dic n < Pin − (2).
Результирующий коммутативный квадрат подгрупп для Spin(2), Pin + (2), SO(2), O(2) – а именно C 2 n , Dih 2 n , C n , Dih n – также получается с помощью проективной ортогональной группы (спускаясь от O на двукратное частное, а не поднимаясь на двукратное накрытие) в квадрате SO(2), O(2), PSO(2), PO(2), хотя в этом случае он также реализуется геометрически, как «проективизация 2 n -угольника в окружности является n -угольником в проективной прямой».
В 3 измерениях ситуация выглядит следующим образом. Алгебра Клиффорда, порожденная 3 антикоммутирующими квадратными корнями из +1, является алгеброй комплексных матриц 2×2, а Pin + (3) изоморфна . [3] Алгебра Клиффорда, порожденная 3 антикоммутирующими квадратными корнями из -1, является алгеброй , а Pin − (3) изоморфна SU(2) × C 2 . Эти группы неизоморфны, поскольку центр Pin + (3) — это C 4 , а центр Pin − (3) — это C 2 × C 2 .
Центр
Предположим . Центром является когда , и когда . Центром является когда , и когда .
Имя
Название было введено в (Atiyah, Bott & Shapiro 1964, страница 3, строка 17), где они утверждают: «Эта шутка принадлежит JP. Serre ». Это обратная формация от Spin: «Pin относится к O( n ), как Spin относится к SO( n )», поэтому, отбрасывая «S» из «Spin», получаем «Pin».
Примечания
- ^ На самом деле они равны как подмножества GL( V ), а не просто изоморфны как абстрактные группы: оператор сохраняет форму тогда и только тогда, когда он сохраняет отрицательную форму.
- ^ Они включены в разные алгебры , но они равны как подмножества векторных пространств и имеют одинаковую структуру произведения, поэтому они естественным образом отождествляются.
- ^ A. Trautman (2001). "Двойные покрытия псевдоортогональных групп". В F. Brackx; JSR Chisholm; V. Souček (ред.). Анализ Клиффорда и его приложения . Серия NATO Science. Том 25. С. 377–388. doi :10.1007/978-94-010-0862-4_32. ISBN 978-0-7923-7045-1.
Ссылки
- ^ Лоусон и Михельсон 1989, стр. 18
- ^ Лоусон и Михельсон 1989, стр. 16–20
- ^ Харви 1990, стр. 302
- Атья, М. Ф.; Ботт , Р .; Шапиро, А. (1964), «Модули Клиффорда», Топология , 3, доп. 1: 3–38, doi :10.1016/0040-9383(64)90003-5
- М. Каруби (1968). «Алгебра Клиффорда и К-теория». Энн. наук. Эк. Норм. Супер . 1 (2): 161–270. дои : 10.24033/asens.1163 .
- Дабровский, Л. (1988), Групповые действия на спинорах , Библиополис, ISBN 88-7088-205-5
- Карлип, С.; ДеВитт-Моретт, К. (1988), «Где знак метрики имеет значение», Phys. Rev. Lett. , 60 (16): 1599–1601, Bibcode : 1988PhRvL..60.1599C, doi : 10.1103/physrevlett.60.1599, PMID 10038088
- Чамблин, А. (1994), «О препятствиях к не-Клиффордовым штифтовым структурам», Comm. Math. Phys. , 164 (1): 65–85, arXiv : gr-qc/9509039 , Bibcode : 1994CMaPh.164...65C, doi : 10.1007/bf02108806, S2CID 18305909
- Харви, Ф. Риз (1990), Спиноры и калибровки , Academic Press, ISBN 978-0-12-329650-4
- Лоусон, Х. Блейн; Михельсон, Мари-Луиз (1989). Геометрия спина . Princeton University Press . ISBN 978-0-691-08542-5.
- Каруби, Макс (2008). K-Theory . Springer. стр. 212–214. ISBN 978-3-540-79889-7.








































