Гравитационная постоянная
| Значение G | Единица |
|---|---|
| 6,674 30 (15) × 10 −11 [ 1] | Н ⋅ м 2 ⋅ кг −2 |
| 6,674 30 (15) × 10 −8 | дин ⋅ см 2 ⋅ г −2 |
| 4,300 917 2706 (3) × 10 −3 | пк ⋅ М ⊙ −1 ⋅( км / с ) 2 |

Гравитационная постоянная — эмпирическая физическая константа , участвующая в расчете гравитационных эффектов в законе всемирного тяготения сэра Исаака Ньютона и в общей теории относительности Альберта Эйнштейна . Она также известна как универсальная гравитационная постоянная , ньютоновская гравитационная постоянная или гравитационная постоянная Кавендиша , [a] обозначается заглавной буквой G.
В законе Ньютона это константа пропорциональности, связывающая гравитационную силу между двумя телами с произведением их масс на обратный квадрат их расстояния . В уравнениях поля Эйнштейна это количественно определяет связь между геометрией пространства-времени и тензором энергии-импульса (также называемым тензором энергии-импульса ).
Измеренное значение константы известно с некоторой точностью до четырех значащих цифр. В единицах СИ его значение приблизительно равно6,6743 × 10−11 Н⋅м 2 / кг 2 . [1]
Современная запись закона Ньютона с использованием G была введена в 1890-х годах CV Boys . Первое неявное измерение с точностью около 1% приписывается Генри Кавендишу в эксперименте 1798 года . [b]
Определение
Согласно закону всемирного тяготения Ньютона , величина силы притяжения ( F ) между двумя телами, каждое из которых имеет сферически симметричное распределение плотности , прямо пропорциональна произведению их масс , m1 и m2 , и обратно пропорциональна квадрату расстояния , r , направленного вдоль линии, соединяющей их центры масс : Константа пропорциональности , G , в этой нерелятивистской формулировке является гравитационной постоянной. В разговорной речи гравитационная постоянная также называется «Большой G», в отличие от «малой g» ( g ) , которая является локальным гравитационным полем Земли (также называемым ускорением свободного падения). [2] [3] Где — масса Земли , а — радиус Земли , эти две величины связаны соотношением:
Гравитационная постоянная появляется в уравнениях поля Эйнштейна общей теории относительности , [4] [5] где G μν — тензор Эйнштейна (не гравитационная постоянная, несмотря на использование G ), Λ — космологическая постоянная , g μν — метрический тензор , T μν — тензор энергии-импульса , а κ — гравитационная постоянная Эйнштейна , константа, первоначально введенная Эйнштейном , которая напрямую связана с ньютоновской постоянной тяготения: [5] [6] [c]
Ценность и неопределенность
Гравитационная постоянная — это физическая константа, которую трудно измерить с высокой точностью. [7] Это происходит потому, что гравитационная сила является чрезвычайно слабой силой по сравнению с другими фундаментальными силами в лабораторных масштабах. [d]
В единицах СИ рекомендуемое CODATA значение гравитационной постоянной составляет: [1]
- =6,674 30 (15) × 10 −11 м 3 ⋅кг −1 ⋅с −2
Относительная стандартная неопределенность равна2,2 × 10−5 .
Натуральные единицы
Из-за его использования в качестве определяющей константы в некоторых системах естественных единиц , в частности, геометризированных системах единиц , таких как единицы Планка и единицы Стони , значение гравитационной постоянной, как правило, будет иметь числовое значение 1 или значение, близкое к нему, если оно выражено в терминах этих единиц. Из-за значительной неопределенности в измеренном значении G в терминах других известных фундаментальных констант, аналогичный уровень неопределенности будет проявляться в значении многих величин, если оно выражено в такой системе единиц.
Орбитальная механика
В астрофизике удобно измерять расстояния в парсеках (пк), скорости в километрах в секунду (км/с) и массы в солнечных единицах M ⊙ . В этих единицах гравитационная постоянная равна: Для ситуаций, когда важны приливы, соответствующими масштабами длины являются солнечные радиусы , а не парсеки. В этих единицах гравитационная постоянная равна: В орбитальной механике период P объекта на круговой орбите вокруг сферического объекта подчиняется , где V — объем внутри радиуса орбиты, а M — общая масса двух объектов. Отсюда следует, что
Такой способ выражения G показывает связь между средней плотностью планеты и периодом обращения спутника над ее поверхностью.
Для эллиптических орбит, применяя 3-й закон Кеплера , выраженный в единицах, характерных для орбиты Земли :
где расстояние измеряется в терминах большой полуоси земной орбиты ( астрономическая единица , а.е.), время в годах , а масса в общей массе орбитальной системы ( M = M ☉ + M E + M ☾ [e] ).
Приведенное выше уравнение является точным только в приближении орбиты Земли вокруг Солнца как задачи двух тел в ньютоновской механике; измеренные величины содержат поправки от возмущений от других тел в Солнечной системе и от общей теории относительности.
Однако с 1964 по 2012 год оно использовалось в качестве определения астрономической единицы и, таким образом, сохраняло свое значение: с 2012 года а.е. определяется как1,495 978 707 × 10 11 м точно, и уравнение больше не может считаться верным.
Величина GM — произведение гравитационной постоянной и массы данного астрономического тела, такого как Солнце или Земля, — известна как стандартный гравитационный параметр (также обозначается μ ). Стандартный гравитационный параметр GM появляется, как указано выше, в законе всемирного тяготения Ньютона, а также в формулах для отклонения света, вызванного гравитационным линзированием , в законах Кеплера о движении планет и в формуле для скорости убегания .
Эта величина дает удобное упрощение различных формул, связанных с гравитацией. Произведение GM известно гораздо точнее, чем любой из факторов.
| Тело | μ = ГМ | Ценить | Относительная неопределенность |
|---|---|---|---|
| Солнце | Г М ☉ | 1,327 124 400 18 (8) × 10 20 м 3 ⋅с −2 [8] | 6 × 10 −11 |
| Земля | Г М Э | 3,986 004 418 (8) × 10 14 м 3 ⋅с −2 [9] | 2 × 10−9 |
Расчеты в небесной механике также могут быть выполнены с использованием единиц солнечных масс , средних солнечных суток и астрономических единиц вместо стандартных единиц СИ. Для этой цели исторически широко использовалась гауссова гравитационная постоянная , k =0,017 202 098 95 радиан в день , что выражает среднюю угловую скорость системы Солнце-Земля. [ необходима ссылка ] Использование этой константы и подразумеваемого определения астрономической единицы, обсуждавшегося выше, было отклонено МАС с 2012 года. [ необходима ссылка ]
История измерений
Ранняя история
Существование константы подразумевается в законе всемирного тяготения Ньютона , опубликованном в 1680-х годах (хотя его обозначение как G датируется 1890-ми годами), [10] но не вычисляется в его Philosophiæ Naturalis Principia Mathematica , где он постулирует закон обратных квадратов тяготения. В Principia Ньютон рассматривал возможность измерения силы тяжести путем измерения отклонения маятника вблизи большого холма, но считал, что эффект будет слишком мал, чтобы его можно было измерить. [11] Тем не менее, у него была возможность оценить порядок величины константы, когда он предположил, что «средняя плотность Земли может быть в пять или шесть раз больше плотности воды», что эквивалентно гравитационной постоянной порядка: [12]
- Г ≈(6,7 ± 0,6) × 10−11 м 3 ⋅кг −1 ⋅с − 2
Измерение было предпринято в 1738 году Пьером Бугером и Шарлем Мари де ла Кондамином в их « Перуанской экспедиции ». Бугер преуменьшил значение их результатов в 1740 году, предположив, что эксперимент по крайней мере доказал, что Земля не может быть полой оболочкой , как предполагали некоторые мыслители того времени, включая Эдмонда Галлея . [13]
Эксперимент Шихаллиона , предложенный в 1772 году и завершенный в 1776 году, был первым успешным измерением средней плотности Земли, и, таким образом, косвенно гравитационной постоянной. Результат, сообщенный Чарльзом Хаттоном (1778), предполагал плотность4,5 г/см 3 ( 4+1/2 раз больше плотности воды), примерно на 20% ниже современного значения. [14] Это немедленно привело к оценкам плотностей и масс Солнца , Луны и планет , отправленным Хаттоном Жерому Лаланду для включения в его планетные таблицы. Как обсуждалось выше, установление средней плотности Земли эквивалентно измерению гравитационной постоянной, учитывая средний радиус Земли и среднее ускорение свободного падения на поверхности Земли, путем установки [10] Исходя из этого, результат Хаттона 1778 года эквивалентен G ≈8 × 10−11 м3 ⋅кг − 1 ⋅с − 2 .

Первое прямое измерение гравитационного притяжения между двумя телами в лаборатории было выполнено в 1798 году, через семьдесят один год после смерти Ньютона, Генри Кавендишем . [15] Он определил значение G неявно, используя крутильные весы , изобретенные геологом преподобным Джоном Мичеллом (1753). Он использовал горизонтальную торсионную балку со свинцовыми шариками, инерцию которых (по отношению к постоянной кручения) он мог определить, измеряя время колебания балки. Их слабое притяжение к другим шарикам, размещенным рядом с балкой, можно было обнаружить по отклонению, которое оно вызывало. Несмотря на то, что экспериментальная конструкция принадлежит Мичеллу, эксперимент теперь известен как эксперимент Кавендиша по его первому успешному выполнению Кавендишем.
Заявленной целью Кавендиша было «взвешивание Земли», то есть определение средней плотности Земли и массы Земли . Его результат, ρ 🜨 =5,448(33) г⋅см −3 , соответствует значению G =6,74(4) × 10−11 м3 ⋅кг −1 ⋅с −2 . Это удивительно точно, примерно на 1% выше современного значения (сравнимо с заявленной относительной стандартной неопределенностью 0,6%). [ 16 ]
19 век
Точность измеренного значения G возросла лишь незначительно со времени первоначального эксперимента Кавендиша. [17] G довольно сложно измерить, поскольку гравитация намного слабее других фундаментальных сил, а экспериментальный аппарат невозможно отделить от гравитационного влияния других тел.
Измерения с помощью маятника были проведены Франческо Карлини (1821,4,39 г/см 3 ), Эдвард Сабин (1827,4,77 г/см 3 ), Карло Игнацио Джулио (1841,4,95 г/см 3 ) и Джордж Бидделл Эйри (1854,6,6 г/см 3 ). [18]
Эксперимент Кавендиша был впервые повторен Фердинандом Райхом (1838, 1842, 1853), который нашел значение5,5832(149) г⋅см −3 , [19] что на самом деле хуже результата Кавендиша, отличаясь от современного значения на 1,5%. Корню и Байль (1873) нашли5,56 г⋅см −3 . [20]
Эксперимент Кавендиша, как оказалось, дал более надежные измерения, чем эксперименты с маятником типа «Шихаллион» (отклонение) или «перуанского» (период как функция высоты). Эксперименты с маятником все еще продолжал проводить Роберт фон Штернек (1883, результаты между 5,0 и6,3 г/см 3 ) и Томас Корвин Менденхолл (1880,5,77 г/см 3 ). [21]
Результат Кавендиша был впервые улучшен Джоном Генри Пойнтингом (1891), [22], который опубликовал значение5,49(3) г⋅см −3 , что отличается от современного значения на 0,2%, но совместимо с современным значением в пределах указанной относительной стандартной неопределенности 0,55%. Помимо Пойнтинга, измерения были выполнены CV Boys (1895) [23] и Carl Braun (1897), [24] с совместимыми результатами, предполагающими G =6,66(1) × 10−11 м3 ⋅кг −1 ⋅с −2 . Современное обозначение , включающее постоянную G, было введено Бойсом в 1894 году [10] и стало стандартным к концу 1890-х годов, причем значения обычно приводились в системе СГС . Рихарц и Кригар-Мензель (1898) попытались повторить эксперимент Кавендиша, используя 100 000 кг свинца для притягивающей массы. Точность их результатаОднако 6,683 ( 11) × 10−11 м3 ⋅кг −1 ⋅с −2 имело тот же порядок величины, что и другие результаты того времени. [ 25 ]
Артур Стэнли Маккензи в «Законах гравитации » (1899) рассматривает работу, проделанную в 19 веке. [26] Пойнтинг является автором статьи «Гравитация» в Encyclopaedia Britannica Eleventh Edition (1911). Здесь он приводит значение G =6,66 × 10−11 м3 ⋅кг − 1 ⋅с − 2 с относительной погрешностью 0,2%.
Современная ценность
Пол Р. Хейл (1930) опубликовал значение6,670(5) × 10−11 м 3 ⋅кг − 1 ⋅с − 2 (относительная неопределенность 0,1%), [27] улучшено до6,673(3) × 10−11 м3 ⋅кг − 1 ⋅с −2 (относительная неопределенность 0,045 % = 450 ppm) в 1942 году. [28]
Однако Хейл использовал статистический разброс в качестве своего стандартного отклонения, и он сам признал, что измерения с использованием одного и того же материала дали очень похожие результаты, в то время как измерения с использованием разных материалов дали совершенно разные результаты. Он провел следующие 12 лет после своей статьи 1930 года, чтобы провести более точные измерения, надеясь, что эффект, зависящий от состава, исчезнет, но этого не произошло, как он отметил в своей последней статье 1942 года.
Опубликованные значения G , полученные из высокоточных измерений с 1950-х годов, оставались совместимыми с Heyl (1930), но в пределах относительной неопределенности около 0,1% (или 1000 ppm) варьировались довольно широко, и не совсем ясно, была ли неопределенность вообще уменьшена с момента измерения 1942 года. Некоторые измерения, опубликованные в 1980-х и 2000-х годах, были фактически взаимоисключающими. [7] [29] Поэтому установление стандартного значения для G с относительной стандартной неопределенностью лучше 0,1% оставалось довольно спекулятивным.
К 1969 году значение, рекомендованное Национальным институтом стандартов и технологий (NIST), было указано с относительной стандартной неопределенностью 0,046% (460 ppm), сниженной до 0,012% (120 ppm) к 1986 году. Однако продолжающаяся публикация противоречивых измерений привела к тому, что NIST значительно увеличил стандартную неопределенность в рекомендованном в 1998 году значении в 12 раз, до стандартной неопределенности 0,15%, что больше, чем указано Хейлом (1930).
Неопределенность была снова снижена в 2002 и 2006 годах, но снова повышена на более консервативные 20% в 2010 году, что соответствует относительной стандартной неопределенности в 120 частей на миллион, опубликованной в 1986 году. [30] Для обновления 2014 года CODATA снизила неопределенность до 46 частей на миллион, что составляет менее половины значения 2010 года и на порядок ниже рекомендации 1969 года.
В следующей таблице показаны рекомендуемые значения NIST, опубликованные с 1969 года:
| Год | G (10 −11 м 3 ⋅кг −1 ⋅с −2 ) | Относительная стандартная неопределенность | Ссылка. |
|---|---|---|---|
| 1969 | 6.6732(31) | 460 частей на миллион | [31] |
| 1973 | 6.6720(49) | 730 частей на миллион | [32] |
| 1986 | 6.67449(81) | 120 частей на миллион | [33] |
| 1998 | 6.673(10) | 1500 частей на миллион | [34] |
| 2002 | 6.6742(10) | 150 частей на миллион | [35] |
| 2006 | 6.67428(67) | 100 частей на миллион | [36] |
| 2010 | 6.67384(80) | 120 частей на миллион | [37] |
| 2014 | 6.67408(31) | 46 частей на миллион | [38] |
| 2018 | 6.67430(15) | 22 частей на миллион | [39] |
| 2022 | 6.67430(15) | 22 частей на миллион | [40] |
В выпуске журнала Science за январь 2007 года Фикслер и др. описали измерение гравитационной постоянной с помощью нового метода — атомной интерферометрии , получив значение G =6,693(34) × 10−11 м3 ⋅кг −1 ⋅с −2 , на 0,28% (2800 ppm ) выше значения CODATA 2006 года. [41] Улучшенное измерение холодных атомов Рози и др. было опубликовано в 2014 году для G =6,671 91 (99) × 10−11 м3 ⋅кг −1 ⋅с −2 . [42] [ 43] Хотя этот результат гораздо ближе к принятому значению (что говорит о том, что измерение Фикслера и др. было ошибочным), он оказался на 325 частей на миллион ниже рекомендуемого значения CODATA 2014 года с неперекрывающимися стандартными интервалами неопределенности.
По состоянию на 2018 год ведутся работы по переоценке противоречивых результатов измерений, координируемые NIST, в частности, проводится повторение экспериментов, описанных Куинном и др. (2013). [44]
В августе 2018 года китайская исследовательская группа объявила о новых измерениях, основанных на крутильных весах,6,674 184 (78) × 10 −11 м 3 ⋅кг −1 ⋅с −2 и6,674 484 (78) × 10 −11 м 3 ⋅кг −1 ⋅с −2 на основе двух различных методов. [45] Они заявляются как самые точные измерения, когда-либо сделанные, со стандартной неопределенностью, указанной на уровне 12 ppm. Разница в 2,7 σ между двумя результатами предполагает, что могут быть неучтенные источники ошибок.
Постоянство
Анализ наблюдений 580 сверхновых типа Ia показывает, что гравитационная постоянная изменялась менее чем на одну десятимиллиардную часть в год за последние девять миллиардов лет. [46]
Смотрите также
Ссылки
- Сноски
- ^ «Ньютоновская постоянная тяготения» — название, введенное для G Бойзом (2000). Термин, использованный Т. Э. Стерном (1928), был неверно процитирован как «Ньютоновская постоянная тяготения» в Pure Science Reviewed for Profound and Unsophisticated Students (1930), что, по-видимому, является первым использованием этого термина. Использование «Ньютоновской постоянной» (без указания «гравитации» или «тяготения») появилось позднее, поскольку «Ньютоновская постоянная» также использовалась для коэффициента теплопередачи в законе охлаждения Ньютона , но к настоящему времени стало довольно распространенным, например, Calmet et al, Quantum Black Holes (2013), стр. 93; P. de Aquino, Beyond Standard Model Phenomenology at the LHC (2013), стр. 3. Название «гравитационная постоянная Кавендиша», иногда «гравитационная постоянная Ньютона–Кавендиша», по-видимому, было распространено в 1970–1980-х годах, особенно в (переводах) советской русской литературы, например, Сагитов (1970 [1969]), Советская физика: Успехи наук 30 (1987), Выпуски 1–6, с. 342 [и т. д.]. «Константа Кавендиша» и «гравитационная постоянная Кавендиша» также используются в работах Чарльза В. Мизнера, Кипа С. Торна, Джона Арчибальда Уиллера, «Гравитация», (1973), 1126f. Разговорное использование «Big G», в отличие от « little g » для обозначения гравитационного ускорения, датируется 1960-ми годами (RW Fairbridge, The encyclopedia of atmosphere sciences and astrogeology , 1967, p. 436; обратите внимание на использование «Big G's» против «little g's» еще в 1940-х годах в тензоре Эйнштейна G μν против метрического тензора g μν , Научные, медицинские и технические книги, изданные в Соединенных Штатах Америки: избранный список названий в печати с аннотациями: приложение к книгам, изданным в 1945–1948 годах , Комитет по американской научной и технической библиографии Национального исследовательского совета, 1950, p. 26).
- ^ Кавендиш определил значение G косвенно, указав значение массы Земли или средней плотности Земли, как5,448 г⋅см −3 .
- ^ В зависимости от выбора определения тензора Эйнштейна и тензора энергии-импульса его можно альтернативно определить как κ = 8π Г/с 2 ≈1,866 × 10−26 м⋅кг − 1
- ^ Например, гравитационная сила между электроном и протоном на расстоянии 1 м составляет приблизительно10 −67 Н , тогда как электромагнитная сила между теми же двумя частицами составляет приблизительно10 −28 Н. Электромагнитная сила в этом примере в 10 39 раз больше силы тяжести — примерно такое же отношение, как масса Солнца к микрограмму.
- ^ M ≈ 1,000003040433 M ☉ , так что M = M ☉ можно использовать для точности в пять или менее значимых цифр.
- Цитаты
- ^ abc "Значение CODATA 2022: Ньютоновская постоянная тяготения". Справочник NIST по константам, единицам и неопределенности . NIST . Май 2024. Получено 18 мая 2024 .
- ^ Gundlach, Jens H.; Merkowitz, Stephen M. (23 декабря 2002 г.). "Измерение Большого G в Вашингтонском университете". Отделение астрофизических наук . Центр космических полетов имени Годдарда.
С тех пор как Кавендиш впервые измерил Гравитационную постоянную Ньютона 200 лет назад, "Большой G" остается одной из самых неуловимых констант в физике.
- ^ Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (сентябрь 2007 г.). Основы физики (8-е изд.). John Wiley & Sons, Limited. стр. 336. ISBN 978-0-470-04618-0.
- ^ Грён, Эйвинд; Хервик, Сигбьорн (2007). Общая теория относительности Эйнштейна: с современными приложениями в космологии (иллюстрированное издание). Springer Science & Business Media. стр. 180. ISBN 978-0-387-69200-5.
- ^ ab Эйнштейн, Альберт (1916). «Основание общей теории относительности». Annalen der Physik . 354 (7): 769–822. Bibcode : 1916AnP...354..769E. doi : 10.1002/andp.19163540702. Архивировано из оригинала ( PDF ) 6 февраля 2012 г.
- ^ Адлер, Рональд; Базен, Морис; Шиффер, Менахем (1975). Введение в общую теорию относительности (2-е изд.). Нью-Йорк: McGraw-Hill. стр. 345. ISBN 978-0-07-000423-8.
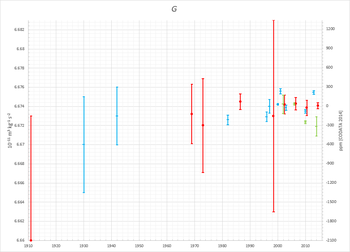
- ^ ab Gillies, George T. (1997). "Ньютоновская гравитационная постоянная: недавние измерения и связанные с ними исследования". Reports on Progress in Physics . 60 (2): 151–225. Bibcode :1997RPPh...60..151G. doi :10.1088/0034-4885/60/2/001. S2CID 250810284.. Длинный, подробный обзор. См. Рисунок 1 и Таблицу 2 в частности.
- ^ "Астродинамические константы". NASA / JPL . 27 февраля 2009 г. Получено 27 июля 2009 г.
- ^ "Геоцентрическая гравитационная постоянная". Числовые стандарты для фундаментальной астрономии . Рабочая группа I отдела МАС по числовым стандартам для фундаментальной астрономии . Получено 24 июня 2021 г. – через iau-a3.gitlab.io.Ссылаясь
- ^ abc Boys 1894, стр.330 В этой лекции перед Королевским обществом Бойс представляет G и приводит доводы в пользу его принятия. См.: Poynting 1894, стр. 4, MacKenzie 1900, стр.vi
- ^ Дэвис, РД (1985). «Памяти Маскелина в Шихаллионе». Ежеквартальный журнал Королевского астрономического общества . 26 (3): 289–294. Bibcode : 1985QJRAS..26..289D.
- ^ «Сэр Исаак Ньютон считал вероятным, что средняя плотность Земли может быть в пять или шесть раз больше плотности воды; и теперь мы обнаружили экспериментально, что она лишь немногим меньше того, что он предполагал: так много справедливости было даже в предположениях этого замечательного человека!» Хаттон (1778), стр. 783
- ^ Пойнтинг, Дж. Х. (1913). Земля: ее форма, размер, вес и вращение. Кембридж. С. 50–56.
- ^ Хаттон, К. (1778). «Отчет о расчетах, сделанных на основе обследования и измерений, проведенных в Шехаллиене». Философские труды Королевского общества . 68 : 689–788. doi : 10.1098/rstl.1778.0034 .
- ↑ Опубликовано в Philosophical Transactions of the Royal Society (1798); переиздание: Кавендиш, Генри (1798). «Эксперименты по определению плотности Земли». В MacKenzie, AS, Scientific Memoirs Vol. 9: The Laws of Gravitation . American Book Co. (1900), стр. 59–105.
- ^ Значение CODATA 2014 г.6,674 × 10−11 м3 ⋅кг − 1 ⋅с − 2 .
- ^ Браш, Стивен Г.; Холтон, Джеральд Джеймс (2001). Физика, человеческое приключение: от Коперника до Эйнштейна и далее . Нью-Брансуик, Нью-Джерси: Издательство Ратгерского университета. С. 137. ISBN 978-0-8135-2908-0.Ли, Дженнифер Лорен (16 ноября 2016 г.). «Big G Redux: решение тайны озадачивающего результата». NIST .
- ↑ Пойнтинг, Джон Генри (1894). Средняя плотность Земли. Лондон: Чарльз Гриффин. С. 22–24.
- ↑ Ф. Райх, «О повторении опытов Кавендиша по определению средней плотности Земли», Философский журнал 12: 283–284.
- ↑ Маккензи (1899), стр. 125.
- ^ А. С. Маккензи, Законы тяготения (1899), 127f.
- ^ Пойнтинг, Джон Генри (1894). Средняя плотность Земли. Герштейн - Университет Торонто. Лондон.
- ↑ Boys, CV (1 января 1895 г.). «О ньютоновской постоянной тяготения». Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences . 186. The Royal Society: 1–72. Bibcode : 1895RSPTA.186....1B. doi : 10.1098/rsta.1895.0001 . ISSN 1364-503X.
- ^ Карл Браун, Denkschriften der k. Акад. д. Висс. (Вена), мат. ты. натурвисс. Классе , 64 (1897). Браун (1897) привел оптимистичную относительную стандартную неопределенность в 0,03%:6,649(2) × 10−11 м3 ⋅кг − 1 ⋅с −2 , но его результат был значительно хуже 0,2%, достижимых в то время.
- ↑ Сагитов, М. У., «Современное состояние определений гравитационной постоянной и массы Земли», Советская астрономия, т. 13 (1970), 712–718, перевод с Астрономического журнала, т. 46, № 4 (июль–август 1969), 907–915 (таблица исторических экспериментов, стр. 715).
- ↑ Маккензи, А. Стэнли, Законы тяготения; мемуары Ньютона, Буге и Кавендиша, вместе с отрывками из других важных мемуаров , American Book Company (1900 [1899]).
- ^ Heyl, PR (1930). «Переопределение постоянной гравитации». Журнал исследований Бюро стандартов . 5 (6): 1243–1290. doi : 10.6028/jres.005.074 .
- ^ PR Heyl и P. Chrzanowski (1942), цитируется по Sagitov (1969:715).
- ^ Mohr, Peter J.; Taylor, Barry N. (2012). "CODATA recommended values of the fundamental physical constants: 2002" (PDF) . Reviews of Modern Physics . 77 (1): 1–107. arXiv : 1203.5425 . Bibcode :2005RvMP...77....1M. CiteSeerX 10.1.1.245.4554 . doi :10.1103/RevModPhys.77.1. Архивировано из оригинала (PDF) 6 марта 2007 г. . Получено 1 июля 2006 г. . В разделе Q (стр. 42–47) описываются взаимно противоречивые измерительные эксперименты, из которых было получено значение CODATA для G.
- ^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (13 ноября 2012 г.). «CODATA recommended values of the fundamental physical constants: 2010» (PDF) . Reviews of Modern Physics . 84 (4): 1527–1605. arXiv : 1203.5425 . Bibcode :2012RvMP...84.1527M. CiteSeerX 10.1.1.150.3858 . doi :10.1103/RevModPhys.84.1527. S2CID 103378639.
- ^ Тейлор, Б. Н.; Паркер, WH; Лангенберг, DN (1 июля 1969 г.). «Определение e / h с использованием макроскопической квантовой фазовой когерентности в сверхпроводниках: последствия для квантовой электродинамики и фундаментальных физических констант». Обзоры современной физики . 41 (3). Американское физическое общество (APS): 375–496. Bibcode : 1969RvMP...41..375T. doi : 10.1103/revmodphys.41.375. ISSN 0034-6861.
- ^ Коэн, Э. Ричард; Тейлор, Б. Н. (1973). «Подгонка фундаментальных констант методом наименьших квадратов 1973 года». Журнал справочных данных по физике и химии . 2 (4). AIP Publishing: 663–734. Bibcode : 1973JPCRD...2..663C. doi : 10.1063/1.3253130. hdl : 2027/pst.000029951949 . ISSN 0047-2689.
- ^ Коэн, Э. Ричард; Тейлор, Барри Н. (1 октября 1987 г.). «Корректировка фундаментальных физических констант в 1986 г.». Reviews of Modern Physics . 59 (4). Американское физическое общество (APS): 1121–1148. Bibcode : 1987RvMP...59.1121C. doi : 10.1103/revmodphys.59.1121. ISSN 0034-6861.
- ^ Mohr, Peter J.; Taylor, Barry N. (2012). «CODATA recommended values of the fundamental physical constants: 1998». Reviews of Modern Physics . 72 (2): 351–495. arXiv : 1203.5425 . Bibcode : 2000RvMP...72..351M. doi : 10.1103/revmodphys.72.351. ISSN 0034-6861.
- ^ Mohr, Peter J.; Taylor, Barry N. (2012). «CODATA recommended values of the fundamental physical constants: 2002». Reviews of Modern Physics . 77 (1): 1–107. arXiv : 1203.5425 . Bibcode : 2005RvMP...77....1M. doi : 10.1103/revmodphys.77.1. ISSN 0034-6861.
- ^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). «CODATA recommended values of the fundamental physical constants: 2006». Journal of Physical and Chemical Reference Data . 37 (3): 1187–1284. arXiv : 1203.5425 . Bibcode : 2008JPCRD..37.1187M. doi : 10.1063/1.2844785. ISSN 0047-2689.
- ^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). «CODATA Recommended Values of the Fundamental Physical Constants: 2010». Journal of Physical and Chemical Reference Data . 41 (4): 1527–1605. arXiv : 1203.5425 . Bibcode : 2012JPCRD..41d3109M. doi : 10.1063/1.4724320. ISSN 0047-2689.
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (2016). «CODATA Recommended Values of the Fundamental Physical Constants: 2014». Journal of Physical and Chemical Reference Data . 45 (4): 1527–1605. arXiv : 1203.5425 . Bibcode : 2016JPCRD..45d3102M. doi : 10.1063/1.4954402. ISSN 0047-2689.
- ^ Eite Tiesinga, Peter J. Mohr, David B. Newell и Barry N. Taylor (2019), "The 2018 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 8.0). База данных разработана J. Baker, M. Douma и S. Kotochigova . Национальный институт стандартов и технологий, Гейтерсберг, Мэриленд 20899.
- ^ Mohr, P.; Tiesinga, E.; Newell, D.; Taylor, B. (8 мая 2024 г.), Codata Internationally Recommended 2022 Values of the Fundamental Physical Constants , дата обращения 15 мая 2024 г.
- ^ Fixler, JB; Foster, GT; McGuirk, JM; Kasevich, MA (5 января 2007 г.). "Измерение ньютоновской постоянной тяжести с помощью атомного интерферометра". Science . 315 (5808): 74–77. Bibcode :2007Sci...315...74F. doi :10.1126/science.1135459. PMID 17204644. S2CID 6271411.
- ^ Рози, Г.; Соррентино, Ф.; Каччиапуоти, Л.; Преведелли, М.; Тино, ГМ (26 июня 2014 г.). «Точное измерение ньютоновской гравитационной постоянной с использованием холодных атомов» (PDF) . Nature . 510 (7506): 518–521. arXiv : 1412.7954 . Bibcode :2014Natur.510..518R. doi :10.1038/nature13433. PMID 24965653. S2CID 4469248. Архивировано (PDF) из оригинала 9 октября 2022 г.
- ^ Шламмингер, Стефан (18 июня 2014 г.). «Фундаментальные константы: классный способ измерить большое G» (PDF) . Nature . 510 (7506): 478–480. Bibcode :2014Natur.510..478S. doi : 10.1038/nature13507 . PMID 24965646. Архивировано (PDF) из оригинала 9 октября 2022 г.
- ^ C. Rothleitner; S. Schlamminger (2017). "Invited Review Article: Measurements of the Newtonian constant of gravitation, G". Review of Scientific Instruments . 88 (11): 111101. Bibcode :2017RScI...88k1101R. doi : 10.1063/1.4994619 . PMC 8195032 . PMID 29195410. 111101.
Однако повторная оценка или повторение уже проведенных экспериментов может дать представление о скрытых предубеждениях или темной неопределенности. У NIST есть уникальная возможность повторить эксперимент Куинна и др. [2013] с почти идентичной установкой. К середине 2018 года исследователи NIST опубликуют свои результаты и присвоят им номер, а также неопределенность.
Ссылка:- T. Quinn; H. Parks; C. Speake; R. Davis (2013). "Улучшенное определение G с использованием двух методов" (PDF) . Phys. Rev. Lett . 111 (10): 101102. Bibcode :2013PhRvL.111j1102Q. doi :10.1103/PhysRevLett.111.101102. PMID 25166649. 101102. Архивировано из оригинала (PDF) 4 декабря 2020 г. . Получено 4 августа 2019 г. .
- ^ Ли, Цин и др. (2018). «Измерения гравитационной постоянной двумя независимыми методами». Nature . 560 (7720): 582–588. Bibcode :2018Natur.560..582L. doi :10.1038/s41586-018-0431-5. PMID 30158607. S2CID 52121922.. См. также: «Физики только что провели самое точное измерение силы гравитации». 31 августа 2018 г. . Получено 13 октября 2018 г. .
- ^ Mould, J.; Uddin, SA (10 апреля 2014 г.). «Ограничение возможной вариации G со сверхновыми типа Ia». Публикации Астрономического общества Австралии . 31 : e015. arXiv : 1402.1534 . Bibcode : 2014PASA...31...15M. doi : 10.1017/pasa.2014.9. S2CID 119292899.
Источники
- Standish., E. Myles (1995). «Отчет подгруппы IAU WGAS по числовым стандартам». В Appenzeller, I. (ред.). Highlights of Astronomy . Дордрехт: Kluwer Academic Publishers. (Полный отчет доступен онлайн: PostScript; PDF. Таблицы из отчета также доступны: Астродинамические константы и параметры)
- Gundlach, Jens H.; Merkowitz, Stephen M. (2000). «Измерение постоянной Ньютона с помощью крутильных весов с обратной связью по угловому ускорению». Physical Review Letters . 85 (14): 2869–2872. arXiv : gr-qc/0006043 . Bibcode : 2000PhRvL..85.2869G. doi : 10.1103/PhysRevLett.85.2869. PMID 11005956. S2CID 15206636.
Внешние ссылки
- Ньютоновская постоянная тяготения G в Национальном институте стандартов и технологий. Ссылки на константы, единицы измерения и неопределенность
- Споры о гравитационной постоянной Ньютона — дополнительные комментарии по проблемам измерения














