Законы Кирхгофа в цепи
Два равенства, которые имеют дело с разностью тока и потенциала

Законы цепей Кирхгофа — это два равенства , которые имеют дело с током и разностью потенциалов (обычно называемой напряжением) в модели сосредоточенных элементов электрических цепей . Они были впервые описаны в 1845 году немецким физиком Густавом Кирхгофом . [1] Это обобщило работу Георга Ома и предшествовало работе Джеймса Клерка Максвелла . Широко используемые в электротехнике , они также называются правилами Кирхгофа или просто законами Кирхгофа . Эти законы могут применяться во временной и частотной областях и составляют основу для анализа сетей .

Оба закона Кирхгофа можно понимать как следствия уравнений Максвелла в пределе низких частот. Они точны для цепей постоянного тока, а также для цепей переменного тока на частотах, где длины волн электромагнитного излучения очень велики по сравнению с цепями.

Текущий закон Кирхгофа

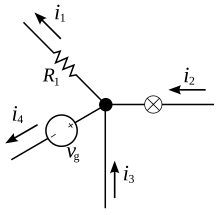
Ток, входящий в любой узел, равен току, выходящему из этого узла. i 2 + i 3 = i 1 + i 4

Этот закон, также называемый первым законом Кирхгофа или правилом узлов Кирхгофа , гласит, что для любого узла (соединения) в электрической цепи сумма токов, втекающих в этот узел, равна сумме токов, вытекающих из этого узла; или, что то же самое:

Алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю.

Учитывая, что ток — это знаковая (положительная или отрицательная) величина, отражающая направление к узлу или от него, этот принцип можно кратко сформулировать так: где n — общее число ветвей с токами, текущими к узлу или от него. ∑ я = 1 н я я = 0 {\displaystyle \sum _{i=1}^{n}I_{i}=0}

Законы Кирхгофа для цепей изначально были получены из экспериментальных результатов. Однако закон тока можно рассматривать как расширение закона сохранения заряда , поскольку заряд является произведением тока и времени, в течение которого ток протекает. Если суммарный заряд в области постоянен, то закон тока будет выполняться на границах области. [2] [3] Это означает, что закон тока основывается на том факте, что суммарный заряд в проводах и компонентах постоянен.

Использует

Матричная версия закона тока Кирхгофа является основой большинства программ моделирования цепей , таких как SPICE . Закон тока используется вместе с законом Ома для выполнения узлового анализа .

Действующий закон применим к любой сосредоточенной сети независимо от характера сети: односторонней или двусторонней, активной или пассивной, линейной или нелинейной.

Закон напряжения Кирхгофа

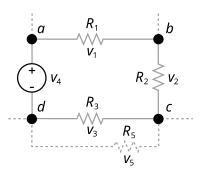
Сумма всех напряжений вокруг контура равна нулю.
v 1 + v 2 + v 3 + v 4 = 0

Этот закон, также называемый вторым законом Кирхгофа или правилом петли Кирхгофа , гласит следующее:

Направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю.

Аналогично закону тока Кирхгофа, закон напряжения можно сформулировать следующим образом: ∑ я = 1 н В я = 0 {\displaystyle \sum _{i=1}^{n}V_{i}=0}

Здесь n — общее количество измеренных напряжений.

Вывод закона Кирхгофа для напряжений

Похожий вывод можно найти в «Лекциях Фейнмана по физике», том II, глава 22: Цепи переменного тока . [3]

Рассмотрим некоторую произвольную цепь. Аппроксимируем цепь сосредоточенными элементами, так что изменяющиеся во времени магнитные поля содержатся в каждом компоненте, а поле в области, внешней по отношению к цепи, пренебрежимо мало. Основываясь на этом предположении, уравнение Максвелла–Фарадея показывает, что во внешней области. Если каждый из компонентов имеет конечный объем, то внешняя область односвязна , и, таким образом, электрическое поле является консервативным в этой области. Следовательно, для любого контура в цепи мы находим, что где есть пути вокруг внешней части каждого из компонентов, от одного вывода до другого. ∇ × Э = − ∂ Б ∂ т = 0 {\displaystyle \nabla \times \mathbf {E} = - {\frac {\partial \mathbf {B} {\partial t}} =\mathbf {0} } ∑ я В я = − ∑ я ∫ П я Э ⋅ г л = ∮ Э ⋅ г л = 0 {\displaystyle \sum _{i}V_{i}=-\sum _{i}\int _{{\mathcal {P}}_{i}}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =\oint \mathbf {E} \cdot \mathrm {d} \mathbf {l} =0} P i {\textstyle {\mathcal {P}}_{i}}

Обратите внимание, что этот вывод использует следующее определение для повышения напряжения от до : a {\displaystyle a} b {\displaystyle b} V a → b = − ∫ P a → b E ⋅ d l {\displaystyle V_{a\to b}=-\int _{{\mathcal {P}}_{a\to b}}\mathbf {E} \cdot \mathrm {d} \mathbf {l} }

Однако электрический потенциал (и, следовательно, напряжение) можно определить и другими способами, например, с помощью разложения Гельмгольца .

Обобщение

В пределе низкой частоты падение напряжения вокруг любой петли равно нулю. Это включает в себя воображаемые петли, расположенные произвольно в пространстве, — не ограничиваясь петлями, очерченными элементами цепи и проводниками. В пределе низкой частоты это следствие закона индукции Фарадея (который является одним из уравнений Максвелла ).

Это имеет практическое применение в ситуациях, связанных со « статическим электричеством ».

Ограничения

Законы цепи Кирхгофа являются результатом модели сосредоточенных элементов , и оба зависят от того, применима ли модель к рассматриваемой цепи. Когда модель неприменима, законы не применяются.

Действующий закон зависит от предположения, что чистый заряд в любом проводе, соединении или сосредоточенном компоненте постоянен. Всякий раз, когда электрическое поле между частями цепи не является пренебрежимо малым, например, когда два провода связаны емкостно , это может быть не так. Это происходит в высокочастотных цепях переменного тока, где модель сосредоточенных элементов больше не применима. [4] Например, в линии передачи плотность заряда в проводнике может постоянно меняться.

В линии передачи суммарный заряд в разных частях проводника меняется со временем. В прямом физическом смысле это нарушает KCL.

С другой стороны, закон напряжения основывается на том факте, что действия изменяющихся во времени магнитных полей ограничены отдельными компонентами, такими как индукторы. В действительности, индуцированное электрическое поле, создаваемое индуктором, не ограничено, но просачивающиеся поля часто пренебрежимо малы.

Моделирование реальных цепей с сосредоточенными элементами

Аппроксимация сосредоточенных элементов для схемы точна на низких частотах. На более высоких частотах утечка потоков и изменение плотности заряда в проводниках становятся значительными. В некоторой степени, все еще возможно моделировать такие схемы с использованием паразитных компонентов . Если частоты слишком высоки, может быть более целесообразным моделировать поля напрямую с помощью моделирования конечных элементов или других методов .

Чтобы моделировать цепи так, чтобы оба закона могли по-прежнему использоваться, важно понимать различие между физическими элементами цепи и идеальными сосредоточенными элементами. Например, провод не является идеальным проводником. В отличие от идеального проводника, провода могут индуктивно и емкостно связываться друг с другом (и с собой) и иметь конечную задержку распространения. Реальные проводники можно моделировать в терминах сосредоточенных элементов, рассматривая паразитные емкости, распределенные между проводниками, для моделирования емкостной связи или паразитные (взаимные) индуктивности для моделирования индуктивной связи. [4] Провода также имеют некоторую самоиндукцию.

Пример

Предположим, что электрическая сеть состоит из двух источников напряжения и трех резисторов.

Согласно первому закону: Применяем второй закон к замкнутой цепи s 1 и заменяем напряжение законом Ома, получаем: Второй закон, снова объединенный с законом Ома, примененный к замкнутой цепи s 2, дает: i 1 − i 2 − i 3 = 0 {\displaystyle i_{1}-i_{2}-i_{3}=0} − R 2 i 2 + E 1 − R 1 i 1 = 0 {\displaystyle -R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}=0} − R 3 i 3 − E 2 − E 1 + R 2 i 2 = 0 {\displaystyle -R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}=0}

Это дает систему линейных уравнений относительно i 1 , i 2 , i 3 : что эквивалентно предположению, что решение имеет вид { i 1 − i 2 − i 3 = 0 − R 2 i 2 + E 1 − R 1 i 1 = 0 − R 3 i 3 − E 2 − E 1 + R 2 i 2 = 0 {\displaystyle {\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}&=0\end{cases}}} { i 1 + ( − i 2 ) + ( − i 3 ) = 0 R 1 i 1 + R 2 i 2 + 0 i 3 = E 1 0 i 1 + R 2 i 2 − R 3 i 3 = E 1 + E 2 {\displaystyle {\begin{cases}i_{1}+(-i_{2})+(-i_{3})&=0\\R_{1}i_{1}+R_{2}i_{2}+0i_{3}&={\mathcal {E}}_{1}\\0i_{1}+R_{2}i_{2}-R_{3}i_{3}&={\mathcal {E}}_{1}+{\mathcal {E}}_{2}\end{cases}}} R 1 = 100 Ω , R 2 = 200 Ω , R 3 = 300 Ω , E 1 = 3 V , E 2 = 4 V {\displaystyle {\begin{aligned}R_{1}&=100\Omega ,&R_{2}&=200\Omega ,&R_{3}&=300\Omega ,\\{\mathcal {E}}_{1}&=3{\text{V}},&{\mathcal {E}}_{2}&=4{\text{V}}\end{aligned}}} { i 1 = 1 1100 A i 2 = 4 275 A i 3 = − 3 220 A {\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}{\text{A}}\\[6pt]i_{2}={\frac {4}{275}}{\text{A}}\\[6pt]i_{3}=-{\frac {3}{220}}{\text{A}}\end{cases}}}

Ток i 3 имеет отрицательный знак, что означает, что предполагаемое направление i 3 было неверным, и i 3 на самом деле течет в направлении, противоположном красной стрелке, обозначенной i 3. Ток в R 3 течет слева направо.

Смотрите также

Ссылки

  1. ^ Олдхэм, Калил Т. Суэйн (2008). Доктрина описания: Густав Кирхгоф, классическая физика и «цель всей науки» в Германии XIX века (Ph. D.). Калифорнийский университет, Беркли. С. 52. Док. 3331743.
  2. ^ Атавле, Прашант. «Закон тока Кирхгофа и закон напряжения Кирхгофа» (PDF) . Университет Джонса Хопкинса . Получено 6 декабря 2018 г. .
  3. ^ ab "Лекции Фейнмана по физике, том II, гл. 22: Цепи переменного тока". feynmanlectures.caltech.edu . Получено 06.12.2018 .
  4. ^ Ральф Моррисон, Методы заземления и экранирования в приборостроении Wiley-Interscience (1986) ISBN 0471838055 
  • Пол, Клейтон Р. (2001). Основы анализа электрических цепей . John Wiley & Sons. ISBN 0-471-37195-5.
  • Serway, Raymond A.; Jewett, John W. (2004). Физика для ученых и инженеров (6-е изд.) . Brooks/Cole. ISBN 0-534-40842-7.
  • Типлер, Пол (2004). Физика для ученых и инженеров: электричество, магнетизм, свет и элементарная современная физика (5-е изд.) . WH Freeman. ISBN 0-7167-0810-8.
  • Грэм, Ховард Джонсон, Мартин (2002). Высокоскоростное распространение сигнала: передовая черная магия (10-е изд.). Аппер Сэдл Ривер, Нью-Джерси: Prentice Hall PTR. ISBN 0-13-084408-X.{{cite book}}: CS1 maint: multiple names: authors list (link)
На Викискладе есть медиафайлы по теме « Законы Кирхгофа» .
  • Разделительные цепи и глава законов Кирхгофа из бесплатной электронной книги Lessons In Electric Circuits Vol 1 DC и серии Lessons In Electric Circuits
Retrieved from "https://en.wikipedia.org/w/index.php?title=Kirchhoff%27s_circuit_laws&oldid=1269352097#Kirchhoff's_voltage_law"