Фаска (геометрия)

Геометрическая операция, которая усекает ребра многогранников.

Куб без фаски, слегка с фаской и с фаской

Исторические модели кристаллов Платоновых тел со слегка скошенными краями

В геометрии , скашивание или усечение ребра — это топологический оператор, который преобразует один многогранник в другой. Он похож на расширение : он раздвигает грани (наружу) и добавляет новую грань между каждыми двумя соседними гранями; но в отличие от расширения, он сохраняет исходные вершины . (Эквивалентно: он разделяет грани, уменьшая их, и добавляет новую грань между каждыми двумя соседними гранями; но он только перемещает вершины внутрь.) Для многогранника эта операция добавляет новую шестиугольную грань вместо каждого исходного ребра .

В нотации многогранников Конвея снятие фаски обозначается буквой «c». Многогранник с $e$ ребрами будет иметь скошенную форму, содержащую $2 e$ новых вершин, $3 e$ новых ребра и $e$ новых шестиугольных граней.

Платоновы тела с фаской

В главах ниже подробно описаны фаски пяти Платоновых тел . Каждая из них показана в равносторонней версии, где все ребра имеют одинаковую длину, и в канонической версии, где все ребра касаются одной и той же средней сферы . (Они выглядят заметно по-разному только для тел, содержащих треугольники.) Показанные двойственные многогранники являются двойственными каноническим версиям.

Семя Платоново тело	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}
Платоново тело с фаской (равносторонняя форма)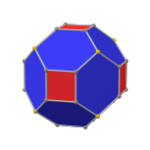

Тетраэдр с фаской

Тетраэдр с фаской
(равносторонняя форма)
нотация Конвея	кТ
многогранник Голдберга	ГП _III (2,0) = {3+,3} _2,0
Лица	4 равных равносторонних треугольника 6 равных равносторонних* шестиугольников
Края	24 (2 типа: треугольник-шестиугольник, шестиугольник-шестиугольник)
Вершины	16 (2 типа)
Конфигурация вершины	(12) 3.6.6 (4) 6.6.6
Группа симметрии	Тетраэдрический (T _d )
Двойной многогранник	Альтернативно-триакистетраэдр
Характеристики	выпуклый , равносторонний*
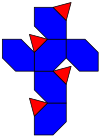Сеть
* для определенной глубины снятия фаски/усечения

Тетраэдр с фаской или альтернативно усеченный куб представляет собой выпуклый многогранник, построенный:

путем снятия фаски с правильного тетраэдра : замена его 6 ребер конгруэнтными сплющенными шестиугольниками;
или путем поочередного усечения (правильного) куба : замены 4 из его 8 вершин конгруэнтными равносторонними треугольными гранями.

При определенной глубине скоса/усечения все (конечные) ребра cT имеют одинаковую длину; тогда шестиугольники являются равносторонними , но не правильными .

Двойственным тетраэдру с фаской является чередующийся триакистетраэдр.

cT — многогранник Голдберга GP _III (2,0) или {3+,3} _2,0 , содержащий треугольные и шестиугольные грани.

Тетраэдрические фаски и их двойственные
тетраэдр с фаской (каноническая форма)	двойник тетратетраэдра	тетраэдр с фаской (каноническая форма)
альтернативно-триакистетраэдр	тетратетраэдр	альтернативно-триакистетраэдр

Куб со скошенной кромкой

Куб со скошенной кромкой
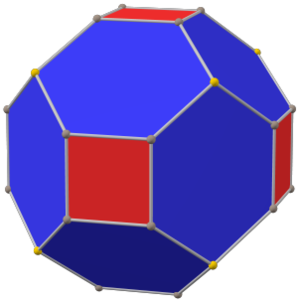(равносторонняя форма)
нотация Конвея	сС = t4daC
многогранник Голдберга	ГП _IV (2,0) = {4+,3} _2,0
Лица	6 равных квадратов 12 равных равносторонних* шестиугольников
Края	48 (2 типа: квадрат-шестиугольник, шестиугольник-шестиугольник)
Вершины	32 (2 типа)
Конфигурация вершины	(24) 4.6.6 (8) 6.6.6
Симметрия	О _ч , [4,3], (432) Т _ч , [4,3 ⁺ ], (32)
Двойной многогранник	Тетракискубооктаэдр
Характеристики	выпуклый , равносторонний*
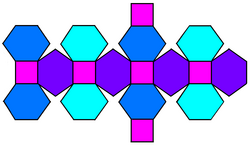Сетка (3 зоны показаны тремя цветами для своих шестиугольников — каждый квадрат находится в 2 зонах —.)
* для определенной глубины фаски

Куб с фаской строится как фаска куба : квадраты уменьшаются в размере, а новые грани, шестиугольники, добавляются вместо всех исходных ребер. cC — это выпуклый многогранник с 32 вершинами, 48 ребрами и 18 гранями: 6 конгруэнтных (и правильных) квадратов и 12 конгруэнтных сплющенных шестиугольников.
Для определенной глубины фаски все (конечные) ребра куба с фаской имеют одинаковую длину; тогда шестиугольники являются равносторонними , но не правильными . Они являются конгруэнтными попеременно усеченными ромбами , имеют 2 внутренних угла и 4 внутренних угла, в то время как правильный шестиугольник имел бы все внутренние углы. $\cos ^{-1}(-{\frac {1}{3}})\approx 109,47^{\circ }$ $\pi -{\frac {1}{2}}\cos ^{-1}(-{\frac {1}{3}})\approx 125,26^{\circ },$ $120^{\circ}$

cC также неточно называют усеченным ромбическим додекаэдром , хотя это название скорее предполагает ромбокубооктаэдр . cC можно более точно назвать тетраусеченным ромбическим додекаэдром , поскольку усечены только вершины (6) порядка 4 ромбического додекаэдра .

Двойственным кубу с фаской является тетракискубооктаэдр .

Поскольку все грани cC имеют четное число сторон и центрально симметричны , он является зоноэдром :

Куб с фаской также является многогранником Голдберга GP _IV (2,0) или {4+,3} _2,0 , содержащим квадратные и шестиугольные грани.

cC — это сумма Минковского ромбического додекаэдра и куба с длиной ребра 1, когда восемь вершин ромбического додекаэдра 3-го порядка находятся в , а его шесть вершин 4-го порядка находятся в перестановках $(\pm 1,\pm 1,\pm 1)$ $(\pm {\sqrt {3}},0,0).$

Топологический эквивалент скошенного куба , но с пиритоэдрической симметрией и прямоугольными гранями, может быть построен путем скашивания осевых ребер пиритоэдра . Это происходит в кристаллах пирита .

Пиритоэдр и его осевое усечение

Исторические кристаллографические модели осей более мелких и более глубоких усечений пиритоэдра

Октаэдрические фаски и их двойники
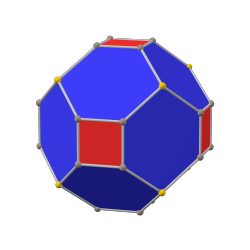куб с фаской (каноническая форма)	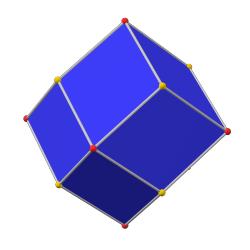ромбический додекаэдр	октаэдр с фаской (каноническая форма)
тетракискубооктаэдр	кубооктаэдр	триакисокубоктаэдр

Октаэдр со скошенной гранью

Октаэдр со скошенной гранью
(равносторонняя форма)
нотация Конвея	cO = t3daO
Лица	8 равных равносторонних треугольников 12 равных равносторонних* шестиугольников
Края	48 (2 типа: треугольник-шестиугольник, шестиугольник-шестиугольник)
Вершины	30 (2 типа)
Конфигурация вершины	(24) 3.6.6 (6) 6.6.6.6
Симметрия	О , [4,3], (*432 ₎
Двойной многогранник	Триакисокубоктаэдр
Характеристики	выпуклый , равносторонний*
* для определенной глубины усечения

В геометрии октаэдр с фаской — это выпуклый многогранник, образованный усечением 8 вершин порядка 3 ромбического додекаэдра . Эти усеченные вершины становятся конгруэнтными равносторонними треугольниками, а исходные 12 ромбических граней становятся конгруэнтными сплющенными шестиугольниками.
Для определенной глубины усечения все (конечные) ребра cO имеют одинаковую длину; тогда шестиугольники являются равносторонними , но не правильными .

Скошенный октаэдр можно также назвать триусеченным ромбическим додекаэдром .

Двойственным к cO является триакискубооктаэдр.

Исторические модели триакискубооктаэдра и слегка скошенного октаэдра

Додекаэдр с фаской

Додекаэдр с фаской
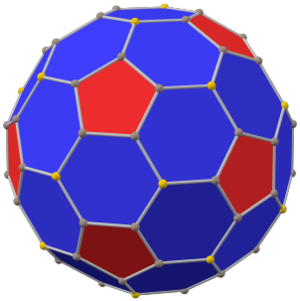(равносторонняя форма)
нотация Конвея	cD = t5daD = dk5aD
многогранник Голдберга	ГП _В (2,0) = {5+,3} _2,0
Фуллерен	С ₈₀^[2]
Лица	12 равных правильных пятиугольников 30 равных равносторонних* шестиугольников
Края	120 (2 типа: пятиугольник-шестиугольник, шестиугольник-шестиугольник)
Вершины	80 (2 типа)
Конфигурация вершины	(60) 5.6.6 (20) 6.6.6
Группа симметрии	Икосаэдрический (I _h )
Двойной многогранник	Пентакис-икосо-додекаэдр
Характеристики	выпуклый , равносторонний*
* для определенной глубины фаски

Фасованный додекаэдр — это выпуклый многогранник с 80 вершинами, 120 ребрами и 42 гранями: 12 конгруэнтных правильных пятиугольников и 30 конгруэнтных сплющенных шестиугольников.
Он построен как фаска правильного додекаэдра . Пятиугольники уменьшены в размере, и новые грани, сплющенные шестиугольники, добавлены на место всех исходных ребер. Для определенной глубины скашивания все (конечные) ребра cD имеют одинаковую длину; тогда шестиугольники являются равносторонними , но не правильными.

cD также неточно называют усеченным ромбическим триаконтаэдром , хотя это название скорее предполагает ромбоикосододекаэдр . cD может быть более точно назван пентаусеченным ромбическим триаконтаэдром , потому что усечены только вершины ромбического триаконтаэдра (12) порядка 5.

Двойственным к додекаэдру с фаской является пентакисикосододекаэдр .

cD — многогранник Голдберга GP _V (2,0) или {5+,3} _2,0 , содержащий пятиугольные и шестиугольные грани.

Икосаэдрические фаски и их двойственные
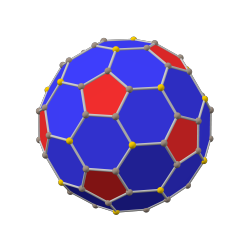додекаэдр с фаской (каноническая форма)	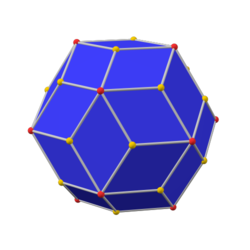ромбический триаконтаэдр	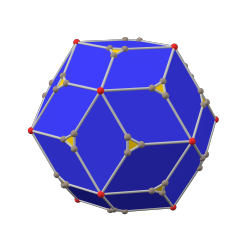икосаэдр с фаской (каноническая форма)
пентакис-икосо-додекаэдр	икосододекаэдр	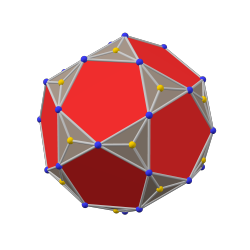триакисикосододекаэдр

Икосаэдр с фаской

Икосаэдр с фаской
(равносторонняя форма)
нотация Конвея	cI = t3daI
Лица	20 равных равносторонних треугольников 30 равных равносторонних* шестиугольников
Края	120 (2 типа: треугольник-шестиугольник, шестиугольник-шестиугольник)
Вершины	72 (2 типа)
Конфигурация вершины	(24) 3.6.6 (12) 6.6.6.6.6
Симметрия	Я _ч , [5,3], (*532)
Двойной многогранник	Триакисикосододекаэдр
Характеристики	выпуклый , равносторонний*
* для определенной глубины усечения

В геометрии скошенный икосаэдр — это выпуклый многогранник, образованный усечением 20 вершин порядка 3 ромбического триаконтаэдра . Шестиугольные грани cI можно сделать равносторонними , но не правильными , с определенной глубиной усечения.

Скошенный икосаэдр можно также назвать триусеченным ромбическим триаконтаэдром .

Двойственным к cI является триакисикосододекаэдр.

Правильная плитка с фаской

Правильные и квазиправильные мозаики с фаской
Квадратная мозаика , Q {4,4}	Треугольная мозаика , Δ {3,6}	Шестиугольная мозаика , H {6,3}	Ромбиль , daH dr{6,3}

cQ	сΔ	чЧ	cdaH

Связь с многогранниками Голдберга

Операция фаски, применяемая последовательно, создает все большие многогранники с новыми гранями, шестиугольными, заменяющими ребра текущего. Оператор фаски преобразует GP(m,n) в GP(2m,2n).

Правильный многогранник GP(1,0) создает последовательность многогранников Голдберга : GP(1,0), GP(2,0), GP(4,0), GP(8,0), GP(16,0)...

	ГП(1,0)	ГП(2,0)	ГП(4,0)	ГП(8,0)	ГП(16,0)	...
ГП _IV {4+,3}	С	сс	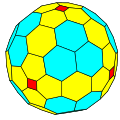ccC	сссС	ccccC	...
ГП _В {5+,3}	Д	компакт-диск	ccD	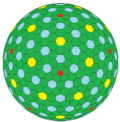cccD	ccccD	...
ГП _VI {6+,3}	ЧАС	чЧ	ccH	сссЧ	ccccH	...

Усеченный октаэдр или усеченный икосаэдр , GP(1,1), создает последовательность Голдберга: GP(1,1), GP(2,2), GP(4,4), GP(8,8)...

	ГП(1,1)	ГП(2,2)	ГП(4,4)	...
ГП _IV {4+,3}	к	ctO	cctO	...
ГП _В {5+,3}	тИ	кти	кстI	...
ГП _VI {6+,3}	тΔ	ctΔ	cctΔ	...

Усеченный тетракисгексаэдр или пентакисдодекаэдр , GP(3,0) , создает последовательность Голдберга: GP(3,0), GP(6,0), GP(12,0)...

	ГП(3,0)	ГП(6,0)	ГП(12,0)	...
ГП _IV {4+,3}	ткС	ctkC	cctkC	...
ГП _В {5+,3}	ткД	ctkD	cctkD	...
ГП _VI {6+,3}	ткХ	ctkH	cctkH	...

Фасованные многогранники и соты

Как и операцию расширения, фаску можно применять к любому размеру.

Для многоугольников это утроит количество вершин. Пример:

Для полихоры новые ячейки создаются вокруг исходных краев. Ячейки — это призмы, содержащие две копии исходной грани, с пирамидами, добавленными к сторонам призмы. ^{[что-то может быть не так в этом отрывке]}

Смотрите также

Ссылки

↑ Spencer 1911, стр. 575 или стр. 597 на Wikisource, КРИСТАЛЛОГРАФИЯ, 1. КУБИЧЕСКАЯ СИСТЕМА, ТЕТРАЭДРИЧЕСКИЙ КЛАСС, ФИГ. 30 и 31.
^ "C80 Isomers". Архивировано из оригинала 2014-08-12 . Получено 2014-08-09 .

Источники

Голдберг, Майкл (1937). «Класс многосимметричных многогранников». Tohoku Mathematical Journal . 43 : 104–108.
Джозеф Д. Клинтон, Гипотеза Клинтона о равном центральном угле [1]
Харт, Джордж (2012). «Многогранники Голдберга». В Сенечал, Марджори (ред.). Shaping Space (2-е изд.). Springer. стр. 125–138. doi :10.1007/978-0-387-92714-5_9. ISBN 978-0-387-92713-8.
Харт, Джордж (18 июня 2013 г.). «Математические впечатления: многогранники Голдберга». Simons Science News.
Антуан Деза, Мишель Деза, Вячеслав Гришухин, Фуллерены и координационные многогранники в сравнении с вложениями полукуба , 1998 PDF [2] (стр. 72 Рис. 26. Тетраэдр с фаской)
Деза, А.; Деза, М .; Гришухин, В. (1998), «Фуллерены и координационные многогранники в сравнении с вложениями полукубов», Дискретная математика , 192 (1): 41–80, doi :10.1016/S0012-365X(98)00065-X.
Спенсер, Леонард Джеймс (1911). «Кристаллография» . В Чисхолм, Хью (ред.). Encyclopaedia Britannica . Т. 07 (11-е изд.). Cambridge University Press. С. 569–591.

Внешние ссылки

Тетраэдр с фаской
Скошенные твердые тела
Усечение вершин и ребер Платоновых и Архимедовых тел, приводящее к вершинно-транзитивным многогранникам Ливио Зефиро
Генератор полиэдров VRML ( нотация полиэдров Конвея )
- Модель VRML Куб с фаской
3.2.7 Систематическая нумерация для фуллерена (C80-Ih) [5,6]
Фуллерен С80
1. [3] (Номер 7 -Ih)
2. [4]
Как сделать куб со скошенной гранью

[FOOTNOTESpencer1911575,_or_p._597_on_Wikisource,_CRYSTALLOGRAPHY,_1._CUBIC_SYSTEM,_TETRAHEDRAL_CLASS,_FIGS._30_&_31-1] Spencer 1911, стр. 575 или стр. 597 на Wikisource, КРИСТАЛЛОГРАФИЯ, 1. КУБИЧЕСКАЯ СИСТЕМА, ТЕТРАЭДРИЧЕСКИЙ КЛАСС, ФИГ. 30 и 31.

[2] "C80 Isomers". Архивировано из оригинала 2014-08-12 . Получено 2014-08-09 .