Метод конечных разностей

В численном анализе конечно-разностные методы ( FDM ) представляют собой класс численных методов решения дифференциальных уравнений путем аппроксимации производных конечными разностями . Как пространственная область, так и временная область (если применимо) дискретизируются или разбиваются на конечное число интервалов, а значения решения в конечных точках интервалов аппроксимируются путем решения алгебраических уравнений, содержащих конечные разности и значения из близлежащих точек.

Методы конечных разностей преобразуют обыкновенные дифференциальные уравнения (ODE) или уравнения в частных производных (PDE), которые могут быть нелинейными , в систему линейных уравнений , которые могут быть решены методами матричной алгебры . Современные компьютеры могут эффективно выполнять эти линейные алгебраические вычисления, и это, наряду с их относительной простотой реализации, привело к широкому использованию FDM в современном численном анализе. ^[1] Сегодня FDM являются одним из наиболее распространенных подходов к численному решению PDE, наряду с методами конечных элементов . ^[1]

Для n -кратно дифференцируемой функции по теореме Тейлора разложение в ряд Тейлора задается как$${\displaystyle f(x_{0}+h)=f(x_{0})+{\frac {f'(x_{0})}{1!}}h+{\frac {f^{(2)}(x_{0})}{2!}}h^{2}+\cdots +{\frac {f^{(n)}(x_{0})}{n!}}h^{n}+R_{n}(x),}$$

Где n ! обозначает факториал числа n , а R _n ( x ) — остаточный член, обозначающий разницу между полиномом Тейлора степени n и исходной функцией.

Ниже приведен процесс получения приближения для первой производной функции f путем предварительного усечения полинома Тейлора плюс остаток: Деление на h дает: Решение относительно :$${\displaystyle f(x_{0}+h)=f(x_{0})+f'(x_{0})h+R_{1}(x).}$$$${\displaystyle {f(x_{0}+h) \over h}={f(x_{0}) \over h}+f'(x_{0})+{R_{1}(x) \over h}}$$${\displaystyle f'(x_{0})}$$${\displaystyle f'(x_{0})={f(x_{0}+h)-f(x_{0}) \over h}-{R_{1}(x) \over h}.}$$

Предполагая, что достаточно мало, приближение первой производной функции f равно:${\displaystyle R_{1}(x)}$$${\displaystyle f'(x_{0})\approx {f(x_{0}+h)-f(x_{0}) \over h}.}$$

Это похоже на определение производной, которое выглядит так: за исключением предела, стремящегося к нулю (в честь этого метода и названо).$${\displaystyle f'(x_{0})=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}.}$$

Погрешность решения метода определяется как разница между приближением и точным аналитическим решением. Двумя источниками ошибок в методах конечных разностей являются ошибка округления , потеря точности из-за компьютерного округления десятичных величин, и ошибка усечения или ошибка дискретизации , разница между точным решением исходного дифференциального уравнения и точной величиной, предполагающей идеальную арифметику (без округления).

Чтобы использовать метод конечных разностей для приближения решения задачи, необходимо сначала дискретизировать область задачи. Обычно это делается путем деления области на равномерную сетку (см. изображение). Это означает, что методы конечных разностей создают наборы дискретных числовых приближений к производной, часто в манере «шага по времени».

Выражение общего интереса — это локальная ошибка усечения метода. Обычно выражаемая с помощью нотации Big-O , локальная ошибка усечения относится к ошибке от одного применения метода. То есть, это величина, если относится к точному значению и к численному приближению. Остаточный член полинома Тейлора может быть использован для анализа локальной ошибки усечения . Используя форму Лагранжа остатка от полинома Тейлора для , который является доминирующим членом локальной ошибки усечения, можно обнаружить. Например, снова используя формулу прямой разности для первой производной, зная, что , и с некоторыми алгебраическими манипуляциями, это приводит к и далее отмечая, что величина слева является приближением из метода конечных разностей, а величина справа является точной величиной интереса плюс остаток, ясно, что остаток является локальной ошибкой усечения. Окончательное выражение этого примера и его порядок:${\displaystyle f'(x_{i})-f'_{i}}$${\displaystyle f'(x_{i})}$${\displaystyle f'_{i}}$${\displaystyle f(x_{0}+h)}$$${\displaystyle R_{n}(x_{0}+h)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(h)^{n+1}\,,\quad x_{0}<\xi <x_{0}+h,}$$${\displaystyle f(x_{i})=f(x_{0}+ih)}$$${\displaystyle f(x_{0}+ih)=f(x_{0})+f'(x_{0})ih+{\frac {f''(\xi )}{2!}}(ih)^{2},}$$$${\displaystyle {\frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+{\frac {f''(\xi )}{2!}}ih,}$$$${\displaystyle {\frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+O(h).}$$

В этом случае локальная ошибка усечения пропорциональна размерам шагов. Качество и продолжительность имитированного решения FDM зависят от выбора уравнения дискретизации и размеров шагов (шагов по времени и пространству). Качество данных и продолжительность моделирования значительно увеличиваются с меньшим размером шага. ^[2] Поэтому для практического использования необходим разумный баланс между качеством данных и продолжительностью моделирования. Большие временные шаги полезны для увеличения скорости моделирования на практике. Однако слишком большие временные шаги могут создавать нестабильности и влиять на качество данных. ^{[3] [4]}

Критерии фон Неймана и Куранта-Фридрихса-Леви часто оцениваются для определения устойчивости числовой модели. ^{[3] [4] [5] [6]}

Например, рассмотрим обыкновенное дифференциальное уравнение. Метод Эйлера для решения этого уравнения использует конечно-разностное отношение для аппроксимации дифференциального уравнения, сначала подставляя его вместо u'(x), а затем применяя немного алгебры (умножая обе части на h, а затем прибавляя u(x) к обеим сторонам), чтобы получить Последнее уравнение является конечно-разностным уравнением, и решение этого уравнения дает приближенное решение дифференциального уравнения.$${\displaystyle u'(x)=3u(x)+2.}$$$${\displaystyle {\frac {u(x+h)-u(x)}{h}}\approx u'(x)}$$$${\displaystyle u(x+h)\approx u(x)+h(3u(x)+2).}$$

Рассмотрим нормализованное уравнение теплопроводности в одном измерении с однородными граничными условиями Дирихле

$${\displaystyle {\begin{cases}U_{t}=U_{xx}\\U(0,t)=U(1,t)=0&{\text{(boundary condition)}}\\U(x,0)=U_{0}(x)&{\text{(initial condition)}}\end{cases}}}$$

Один из способов численного решения этого уравнения — аппроксимировать все производные конечными разностями. Сначала разбейте область в пространстве с помощью сетки и во времени с помощью сетки . Предположим, что разбиение равномерное как в пространстве, так и во времени, так что разница между двумя последовательными точками пространства будет h , а между двумя последовательными точками времени будет k . Точки${\displaystyle x_{0},\dots ,x_{J}}$${\displaystyle t_{0},\dots ,t_{N}}$

$${\displaystyle u(x_{j},t_{n})=u_{j}^{n}}$$

будет представлять численное приближение${\displaystyle u(x_{j},t_{n}).}$

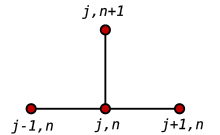
Используя прямую разность по времени и ${\displaystyle t_{n}}$центральную разность второго порядка для пространственной производной в позиции ( FTCS ), получаем рекуррентное уравнение:${\displaystyle x_{j}}$

$${\displaystyle {\frac {u_{j}^{n+1}-u_{j}^{n}}{k\Delta t}}={\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}.}$$

Это явный метод решения одномерного уравнения теплопроводности .

Из других значений можно получить следующее:${\displaystyle u_{j}^{n+1}}$

$${\displaystyle u_{j}^{n+1}=(1-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}}$$

где${\displaystyle r=k\Delta t/h^{2}.}$

Таким образом, используя это рекуррентное соотношение и зная значения в момент времени n , можно получить соответствующие значения в момент времени n +1. и их необходимо заменить граничными условиями, в этом примере они оба равны 0.${\displaystyle u_{0}^{n}}$${\displaystyle u_{J}^{n}}$

Известно, что этот явный метод численно устойчив и сходится всякий раз, когда . ^[7] Численные ошибки пропорциональны временному шагу и квадрату пространственного шага:${\displaystyle r\leq 1/2}$$${\displaystyle \Delta u=O(k)+O(h^{2})}$$

Используя обратную разность по времени${\displaystyle t_{n+1}}$ и центральную разность второго порядка для пространственной производной по позиции (метод обратного времени и центрированного пространства «BTCS»), получаем рекуррентное уравнение:${\displaystyle x_{j}}$

$${\displaystyle {\frac {u_{j}^{n+1}-u_{j}^{n}}{k\Delta t}}={\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}.}$$

Это неявный метод решения одномерного уравнения теплопроводности .

Решив систему линейных уравнений, можно получить :${\displaystyle u_{j}^{n+1}}$

$${\displaystyle (1+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=u_{j}^{n}}$$

Схема всегда численно устойчива и сходится, но обычно более численно интенсивна, чем явный метод, поскольку требует решения системы численных уравнений на каждом временном шаге. Ошибки линейны по временному шагу и квадратичны по пространственному шагу:$${\displaystyle \Delta u=O(k)+O(h^{2}).}$$

Наконец, используя центральную разность по времени и центральную разность второго порядка для пространственной производной в позиции («CTCS»), получаем рекуррентное уравнение:${\displaystyle t_{n+1/2}}$${\displaystyle x_{j}}$

$${\displaystyle {\frac {u_{j}^{n+1}-u_{j}^{n}}{k\Delta t}}={\frac {1}{2}}\left({\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}+{\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}\right).}$$

Эта формула известна как метод Кранка–Николсона .

Решив систему линейных уравнений, можно получить :${\displaystyle u_{j}^{n+1}}$

$${\displaystyle (2+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=(2-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}}$$

Схема всегда численно стабильна и сходится, но обычно более численно интенсивна, поскольку требует решения системы численных уравнений на каждом временном шаге. Ошибки квадратичны как по временному шагу, так и по пространственному шагу:$${\displaystyle \Delta u=O(k^{2})+O(h^{2}).}$$

Подводя итог, обычно схема Кранка–Николсона является наиболее точной схемой для малых временных шагов. Для больших временных шагов неявная схема работает лучше, поскольку она менее требовательна к вычислениям. Явная схема является наименее точной и может быть нестабильной, но также является наиболее простой в реализации и наименее численно интенсивной.

Вот пример. На рисунках ниже представлены решения, полученные с помощью вышеуказанных методов для аппроксимации уравнения теплопроводности.

$${\displaystyle U_{t}=\alpha U_{xx},\quad \alpha ={\frac {1}{\pi ^{2}}},}$$

с граничным условием

$${\displaystyle U(0,t)=U(1,t)=0.}$$

Точное решение:

$${\displaystyle U(x,t)={\frac {1}{\pi ^{2}}}e^{-t}\sin(\pi x).}$$

(Непрерывный) оператор Лапласа в -измерениях задается выражением . Дискретный оператор Лапласа зависит от размерности .${\displaystyle n}$${\displaystyle \Delta u(x)=\sum _{i=1}^{n}\partial _{i}^{2}u(x)}$${\displaystyle \Delta _{h}u}$${\displaystyle n}$

В 1D оператор Лапласа аппроксимируется как Это приближение обычно выражается с помощью следующего шаблона и который представляет собой симметричную трехдиагональную матрицу. Для равноотстоящей сетки получается матрица Теплица .$${\displaystyle \Delta u(x)=u''(x)\approx {\frac {u(x-h)-2u(x)+u(x+h)}{h^{2}}}=:\Delta _{h}u(x)\,.}$$$${\displaystyle \Delta _{h}={\frac {1}{h^{2}}}{\begin{bmatrix}1&-2&1\end{bmatrix}}}$$

Двумерный случай показывает все характеристики более общего n-мерного случая. Каждая вторая частная производная должна быть аппроксимирована аналогично одномерному случаю , который обычно задается следующим шаблоном$${\displaystyle {\begin{aligned}\Delta u(x,y)&=u_{xx}(x,y)+u_{yy}(x,y)\\&\approx {\frac {u(x-h,y)-2u(x,y)+u(x+h,y)}{h^{2}}}+{\frac {u(x,y-h)-2u(x,y)+u(x,y+h)}{h^{2}}}\\&={\frac {u(x-h,y)+u(x+h,y)-4u(x,y)+u(x,y-h)+u(x,y+h)}{h^{2}}}\\&=:\Delta _{h}u(x,y)\,,\end{aligned}}}$$$${\displaystyle \Delta _{h}={\frac {1}{h^{2}}}{\begin{bmatrix}&1\\1&-4&1\\&1\end{bmatrix}}\,.}$$

Согласованность вышеупомянутого приближения может быть показана для высокорегулярных функций, таких как . Утверждение имеет вид${\displaystyle u\in C^{4}(\Omega )}$$${\displaystyle \Delta u-\Delta _{h}u={\mathcal {O}}(h^{2})\,.}$$

Чтобы доказать это, нужно подставить разложения Тейлора до третьего порядка в дискретный оператор Лапласа.

Подобно непрерывным субгармоническим функциям можно определить субгармонические функции для конечно-разностных аппроксимаций.${\displaystyle u_{h}}$$${\displaystyle -\Delta _{h}u_{h}\leq 0\,.}$$

Можно определить общий трафарет позитивного типа через$${\displaystyle {\begin{bmatrix}&\alpha _{N}\\\alpha _{W}&-\alpha _{C}&\alpha _{E}\\&\alpha _{S}\end{bmatrix}}\,,\quad \alpha _{i}>0\,,\quad \alpha _{C}=\sum _{i\in \{N,E,S,W\}}\alpha _{i}\,.}$$

Если является (дискретной) субгармонической, то выполняется следующее свойство среднего значения , где приближение оценивается по точкам сетки, а шаблон предполагается положительным.${\displaystyle u_{h}}$$${\displaystyle u_{h}(x_{C})\leq {\frac {\sum _{i\in \{N,E,S,W\}}\alpha _{i}u_{h}(x_{i})}{\sum _{i\in \{N,E,S,W\}}\alpha _{i}}}\,,}$$

Аналогичное свойство среднего значения справедливо и для непрерывного случая.

Для (дискретной) субгармонической функции справедливо следующее соотношение, где — дискретизации непрерывной области , соответственно, границы .${\displaystyle u_{h}}$$${\displaystyle \max _{\Omega _{h}}u_{h}\leq \max _{\partial \Omega _{h}}u_{h}\,,}$$${\displaystyle \Omega _{h},\partial \Omega _{h}}$${\displaystyle \Omega }$${\displaystyle \partial \Omega }$

Аналогичный принцип максимума справедлив и для непрерывного случая.

Метод SBP-SAT ( суммирование по частям - одновременный приближенный член ) является стабильным и точным методом дискретизации и наложения граничных условий корректно поставленного уравнения в частных производных с использованием конечных разностей высокого порядка. ^{[8] [9]}

Метод основан на конечных разностях, где операторы дифференциации демонстрируют свойства суммирования по частям . Обычно эти операторы состоят из матриц дифференциации с центральными шаблонами разностей внутри с тщательно выбранными односторонними граничными шаблонами, разработанными для имитации интегрирования по частям в дискретной обстановке. При использовании техники SAT граничные условия PDE налагаются слабо, где граничные значения «подтягиваются» к желаемым условиям, а не выполняются точно. Если параметры настройки (присущие технике SAT) выбраны правильно, то полученная система ODE будет демонстрировать такое же энергетическое поведение, как и непрерывное PDE, т. е. система не имеет нефизического роста энергии. Это гарантирует устойчивость, если используется схема интегрирования с областью устойчивости, которая включает части мнимой оси, например, метод Рунге-Кутты четвертого порядка . Это делает технику SAT привлекательным методом наложения граничных условий для методов конечных разностей более высокого порядка, в отличие, например, от метода инъекции, который обычно не будет устойчивым, если используются операторы дифференцирования высокого порядка.

• К. В. Мортон и Д. Ф. Майерс, Численное решение уравнений с частными производными, Введение . Издательство Кембриджского университета, 2005.
• Аутар Кау и Э. Эрик Калу, Численные методы и их приложения , (2008) [1]. Содержит краткое инженерно-ориентированное введение в FDM (для ОДУ) в главе 08.07.
• Джон Стрикверда (2004). Конечно-разностные схемы и уравнения в частных производных (2-е изд.). SIAM. ISBN 978-0-89871-639-9.
• Смит, Г.Д. (1985), Численное решение уравнений с частными производными: методы конечных разностей, 3-е изд. , Oxford University Press
• Питер Олвер (2013). Введение в уравнения с частными производными. Springer. Глава 5: Конечные разности. ISBN 978-3-319-02099-0..
• Рэндалл Дж. Левек , Методы конечных разностей для обыкновенных и частных дифференциальных уравнений , SIAM, 2007.
• Сергей Лемешевский, Петр Матус, Дмитрий Поляков (редакторы): «Точные конечно-разностные схемы», Де Грюйтер (2016). DOI: https://doi.org/10.1515/9783110491326.