Дискретный оператор Лапласа

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Материалы без ссылок могут быть оспорены и удалены. Найти источники:  "Discrete Laplace Operator" – новости  · газеты  · книги  · ученый  · JSTOR ( декабрь 2007 г. ) ( Узнайте, как и когда удалять это сообщение )

В математике дискретный оператор Лапласа является аналогом непрерывного оператора Лапласа , определенного так, чтобы он имел смысл на графе или дискретной сетке . Для случая конечномерного графа (имеющего конечное число ребер и вершин) дискретный оператор Лапласа чаще называют матрицей Лапласа .

Дискретный оператор Лапласа встречается в физических задачах, таких как модель Изинга и петлевая квантовая гравитация , а также при изучении дискретных динамических систем . Он также используется в численном анализе в качестве замены непрерывного оператора Лапласа. Распространенные приложения включают обработку изображений , ^[1] где он известен как фильтр Лапласа , и в машинном обучении для кластеризации и полуконтролируемого обучения на графах соседства.

Существуют различные определения дискретного лапласиана для графов , отличающиеся знаком и масштабным множителем (иногда усредняется по соседним вершинам, иногда просто суммируется; для обычного графа это не имеет значения ). Традиционное определение лапласиана графа, приведенное ниже, соответствует отрицательному непрерывному лапласиану на области со свободной границей.

Пусть будет графом с вершинами и ребрами . Пусть будет функцией вершин, принимающей значения в кольце . Тогда дискретный Лапласиан, действующий на , определяется как${\displaystyle G=(V,E)}$${\displaystyle V}$${\displaystyle E}$${\displaystyle \phi \colon V\to R}$${\displaystyle \Дельта}$${\displaystyle \фи}$

${\displaystyle (\Delta \phi)(v)=\sum _{w:\,d(w,v)=1}\left[\phi (v)-\phi (w)\right]}$

где — расстояние графа между вершинами w и v. Таким образом, эта сумма берется по ближайшим соседям вершины v . Для графа с конечным числом ребер и вершин это определение идентично определению матрицы Лапласа . То есть, может быть записано как вектор-столбец; и так же является произведением вектора-столбца и матрицы Лапласа, в то время как — это просто v' -й элемент вектора-произведения.${\displaystyle d(w,v)}$${\displaystyle \фи}$${\displaystyle \Дельта \фи }$${\displaystyle (\Delta \phi)(v)}$

Если граф имеет взвешенные ребра, то есть задана весовая функция, то определение можно обобщить до${\displaystyle \gamma \colon E\to R}$

${\displaystyle (\Delta _{\gamma }\phi)(v)=\sum _{w:\,d(w,v)=1}\gamma _{wv}\left[\phi (v)- \фи (ш)\вправо]}$

где - значение веса на ребре .${\displaystyle \гамма _{wv}}$${\displaystyle wv\in E}$

С дискретным лапласианом тесно связан оператор усреднения :

${\displaystyle (M\phi)(v)={\frac {1}{\deg v}}\sum _{w:\,d(w,v)=1}\phi (w).}$

В дополнение к рассмотрению связности узлов и ребер в графе, операторы Лапласа сетки учитывают геометрию поверхности (например, углы в узлах). Для двумерной многообразной треугольной сетки оператор Лапласа-Бельтрами скалярной функции в вершине может быть аппроксимирован как${\displaystyle u}$${\displaystyle я}$

${\displaystyle (\Delta u)_{i}\equiv {\frac {1}{2A_{i}}}\sum _{j}(\cot \alpha _{ij}+\cot \beta _{ij})(u_{j}-u_{i}),}$

где сумма берется по всем смежным вершинам , а — два угла, противоположные ребру , а — площадь вершины ; то есть, например, одна треть суммированных площадей треугольников, инцидентных . Важно отметить, что знак дискретного оператора Лапласа-Бельтрами традиционно противоположен знаку обычного оператора Лапласа . Вышеприведенная формула котангенса может быть выведена с использованием множества различных методов, среди которых кусочно-линейные конечные элементы , конечные объемы и дискретное внешнее исчисление ^[2] (загрузка PDF: [1]).${\displaystyle j}$${\displaystyle я}$${\displaystyle \альфа _{ij}}$${\displaystyle \beta _{ij}}$${\displaystyle ij}$${\displaystyle A_{i}}$${\displaystyle я}$${\displaystyle я}$

Для облегчения вычислений лапласиан кодируется в матрице такой, что . Пусть будет (разреженной) котангенсной матрицей с элементами${\displaystyle L\in \mathbb {R} ^{|V|\times |V|}}$${\displaystyle Lu=(\Delta u)_{i}}$${\displaystyle С}$

${\displaystyle C_{ij}={\begin{cases}{\frac {1}{2}}(\cot \alpha _{ij}+\cot \beta _{ij})&ij{\text{ является ребром, то есть }}j\in N(i),\\-\sum \limits _{k\in N(i)}C_{ik}&i=j,\\0&{\text{иначе}}\end{cases}}}$

где обозначает окрестность , а пусть — диагональная матрица масс , -й элемент которой по диагонали — это площадь вершины . Тогда — искомая дискретизация лапласиана.${\displaystyle N(я)}$${\displaystyle я}$${\displaystyle М}$ ${\displaystyle М}$${\displaystyle я}$${\displaystyle A_{i}}$${\displaystyle L=M^{-1}C}$

Более общий обзор операторов сетки дан в ^{[3] .}

Аппроксимации лапласиана , полученные методом конечных разностей или методом конечных элементов , также можно назвать дискретными лапласианами . Например, лапласиан в двух измерениях можно аппроксимировать с помощью метода пятиточечных трафаретных конечных разностей , что даст

${\displaystyle \Delta f(x,y)\approx {\frac {f(xh,y)+f(x+h,y)+f(x,yh)+f(x,y+h)-4f(x,y)}{h^{2}}},}$

где размер сетки равен h в обоих измерениях, так что пятиточечный трафарет точки ( x ,  y ) в сетке равен

${\displaystyle \{(xh,y),(x,y),(x+h,y),(x,yh),(x,y+h)\}.}$

Если размер сетки h = 1, результатом является отрицательный дискретный лапласиан на графике, который является квадратной решетчатой ​​сеткой . Здесь нет ограничений на значения функции f ( x , y ) на границе решетчатой ​​сетки, таким образом, это случай отсутствия источника на границе, то есть граничное условие отсутствия потока (также известное как изоляция или однородное граничное условие Неймана ). Управление переменной состояния на границе, как f ( x , y ), заданное на границе сетки (также известное как граничное условие Дирихле ), редко используется для графовых лапласианов, но распространено в других приложениях.

Многомерные дискретные лапласианы на прямоугольных кубоидных регулярных сетках обладают весьма специальными свойствами, например, они являются суммами Кронекера одномерных дискретных лапласианов, см. Сумма Кронекера дискретных лапласианов , и в этом случае все их собственные значения и собственные векторы могут быть явно вычислены.

В этом подходе область дискретизируется на более мелкие элементы, часто треугольники или тетраэдры, но возможны и другие элементы, такие как прямоугольники или кубоиды. Затем пространство решений аппроксимируется с использованием так называемых форм-функций предопределенной степени. Затем дифференциальное уравнение, содержащее оператор Лапласа, преобразуется в вариационную формулировку, и строится система уравнений (линейные или собственные задачи). Полученные матрицы обычно очень разрежены и могут быть решены итеративными методами.

Дискретный оператор Лапласа часто используется в обработке изображений, например, в приложениях обнаружения краев и оценки движения. ^[4] Дискретный лапласиан определяется как сумма вторых производных оператор Лапласа#Координатные выражения и вычисляется как сумма разностей по ближайшим соседям центрального пикселя. Поскольку производные фильтры часто чувствительны к шуму в изображении, оператору Лапласа часто предшествует сглаживающий фильтр (например, гауссовский фильтр) для удаления шума перед вычислением производной. Сглаживающий фильтр и фильтр Лапласа часто объединяются в один фильтр. ^[5]

Для одно-, двух- и трехмерных сигналов дискретный лапласиан может быть задан в виде свертки со следующими ядрами:

1D фильтр: ,${\displaystyle {\vec {D}}_{x}^{2}={\begin{bmatrix}1&-2&1\end{bmatrix}}}$

2D-фильтр: .${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}}}$

${\displaystyle \mathbf {D} _{xy}^{2}}$соответствует ( пятиточечному трафарету ) конечно-разностной формуле, рассмотренной ранее. Она устойчива для очень плавно меняющихся полей, но для уравнений с быстро меняющимися решениями требуется более устойчивая и изотропная форма оператора Лапласа ^[6] , например, трафарет из девяти точек , который включает диагонали:

2D-фильтр: ,${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}0,25&0,5&0,25\\0,5&-3&0,5\\0,25&0,5&0,25\end{bmatrix}}}$

3D-фильтр: с использованием семиточечного трафарета определяется по формуле:${\displaystyle \mathbf {D} _{xyz}^{2}}$

первая плоскость = ; вторая плоскость = ; третья плоскость = .${\displaystyle {\begin{bmatrix}0&0&0\\0&1&0\\0&0&0\end{bmatrix}}}$${\displaystyle {\begin{bmatrix}0&1&0\\1&-6&1\\0&1&0\end{bmatrix}}}$${\displaystyle {\begin{bmatrix}0&0&0\\0&1&0\\0&0&0\end{bmatrix}}}$

и с использованием 27-точечного трафарета: ^[7]

первая плоскость = ; вторая плоскость = ; третья плоскость = .${\displaystyle {\frac {1}{26}}{\begin{bmatrix}2&3&2\\3&6&3\\2&3&2\end{bmatrix}}}$${\displaystyle {\frac {1}{26}}{\begin{bmatrix}3&6&3\\6&-88&6\\3&6&3\end{bmatrix}}}$${\displaystyle {\frac {1}{26}}{\begin{bmatrix}2&3&2\\3&6&3\\2&3&2\end{bmatrix}}}$

n D фильтр : Для элементаядра${\displaystyle a_{x_{1},x_{2},\dots ,x_{n}}}$${\displaystyle \mathbf {D} _{x_{1},x_{2},\dots ,x_{n}}^{2},}$

${\displaystyle a_{x_{1},x_{2},\dots ,x_{n}}=\left\{{\begin{array}{ll}-2n&{\text{if }}s=n,\\1&{\text{if }}s=n-1,\\0&{\text{otherwise,}}\end{array}}\right.}$

где x _i — позиция ( −1 , 0 или 1 ) элемента в ядре в i -м направлении, а s — количество направлений i, для которых x _i = 0 .

Обратите внимание, что версия n D, основанная на графовом обобщении Лапласа, предполагает, что все соседи находятся на одинаковом расстоянии, и, следовательно, приводит к следующему 2D-фильтру с включенными диагоналями, а не к версии выше:

2D-фильтр:${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}1&1&1\\1&-8&1\\1&1&1\end{bmatrix}}.}$

Эти ядра выводятся с использованием дискретных дифференциальных отношений.

Можно показать ^{[8] [9]} , что следующая дискретная аппроксимация двумерного оператора Лапласа как выпуклой комбинации разностных операторов

${\displaystyle \nabla _{\gamma }^{2}=(1-\gamma )\nabla _{5}^{2}+\gamma \nabla _{\times }^{2}=(1-\gamma ){\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}}+\gamma {\begin{bmatrix}1/2&0&1/2\\0&-2&0\\1/2&0&1/2\end{bmatrix}}}$

для γ ∈ [0, 1] совместимо со свойствами дискретного масштабного пространства, где конкретно значение γ = 1/3 дает наилучшее приближение вращательной симметрии. ^{[8] [9] [10]} Что касается трехмерных сигналов, показано ^[9] , что оператор Лапласа может быть аппроксимирован двухпараметрическим семейством разностных операторов

${\displaystyle \nabla _{\gamma _{1},\gamma _{2}}^{2}=(1-\gamma _{1}-\gamma _{2})\,\nabla _{7}^{2}+\gamma _{1}\,\nabla _{+^{3}}^{2}+\gamma _{2}\,\nabla _{\times ^{3}}^{2}),}$

где

${\displaystyle (\nabla _{7}^{2}f)_{0,0,0}=f_{-1,0,0}+f_{+1,0,0}+f_{0,-1,0}+f_{0,+1,0}+f_{0,0,-1}+f_{0,0,+1}-6f_{0,0,0},}$

${\displaystyle (\nabla _{+^{3}}^{2}f)_{0,0,0}={\frac {1}{4}}(f_{-1,-1,0}+f_{-1,+1,0}+f_{+1,-1,0}+f_{+1,+1,0}+f_{-1,0,-1}+f_{-1,0,+1}+f_{+1,0,-1}+f_{+1,0,+1}+f_{0,-1,-1}+f_{0,-1,+1}+f_{0,+1,-1}+f_{0,+1,+1}-12f_{0,0,0}),}$

${\displaystyle (\nabla _{\times ^{3}}^{2}f)_{0,0,0}={\frac {1}{4}}(f_{-1,-1,-1}+f_{-1,-1,+1}+f_{-1,+1,-1}+f_{-1,+1,+1}+f_{+1,-1,-1}+f_{+1,-1,+1}+f_{+1,+1,-1}+f_{+1,+1,+1}-8f_{0,0,0}).}$

С помощью анализа ряда Тейлора можно показать, что комбинации значений и для которых дают наилучшие приближения вращательной симметрии.${\displaystyle \gamma _{1}}$${\displaystyle \gamma _{2}}$${\displaystyle 3\gamma _{1}+6\gamma _{2}=2}$

Дискретный сигнал, включающий изображения, можно рассматривать как дискретное представление непрерывной функции , где вектор координат и область значений являются действительными . Операция деривации, таким образом, напрямую применима к непрерывной функции, . В частности, любое дискретное изображение с разумными предположениями о процессе дискретизации, например, предполагая функции с ограниченной полосой пропускания или функции, расширяемые вейвлетами и т. д., может быть восстановлено с помощью хорошо ведущих себя интерполяционных функций, лежащих в основе формулы восстановления, ^[11]${\displaystyle f({\bar {r}})}$${\displaystyle {\bar {r}}\in R^{n}}$${\displaystyle f\in R}$${\displaystyle f}$

${\displaystyle f({\bar {r}})=\sum _{k\in K}f_{k}\mu _{k}({\bar {r}})}$

где — дискретные представления на сетке и — интерполяционные функции, специфичные для сетки . На равномерной сетке, такой как изображения, и для функций с ограниченной полосой пропускания интерполяционные функции инвариантны относительно сдвига, что соответствует расширенной функции sinc, определенной в -измерениях, то есть . Другие приближения на равномерных сетках — это расширенные гауссовские функции в -измерениях. Соответственно, дискретный лапласиан становится дискретной версией лапласиана непрерывного${\displaystyle f_{k}\in R}$${\displaystyle f}$${\displaystyle K}$${\displaystyle \mu _{k}}$${\displaystyle K}$${\displaystyle \mu _{k}({\bar {r}})=\mu ({\bar {r}}-{\bar {r}}_{k})}$${\displaystyle \mu }$${\displaystyle n}$${\displaystyle {\bar {r}}=(x_{1},x_{2}...x_{n})^{T}}$${\displaystyle \mu }$${\displaystyle n}$${\displaystyle f({\bar {r}})}$

${\displaystyle \nabla ^{2}f({\bar {r}}_{k})=\sum _{k'\in K}f_{k'}(\nabla ^{2}\mu ({\bar {r}}-{\bar {r}}_{k'}))|_{{\bar {r}}={\bar {r}}_{k}}}$

который в свою очередь является сверткой с лапласианом функции интерполяции на равномерной (изображение) сетке . Преимущество использования гауссианов в качестве функций интерполяции заключается в том, что они дают линейные операторы, включая лапласианы, которые свободны от артефактов вращения системы координат, в которой представлено через , в -измерениях, и по определению учитывают частоту. Линейный оператор имеет не только ограниченный диапазон в области, но и эффективный диапазон в частотной области (альтернативно гауссово масштабное пространство), который может явно контролироваться через дисперсию гауссианы принципиальным образом. Результирующая фильтрация может быть реализована с помощью разделяемых фильтров и представлений децимации (обработки сигнала) / пирамиды (обработки изображений) для дальнейшей вычислительной эффективности в -измерениях. Другими словами, дискретный лапласовский фильтр любого размера может быть удобно сгенерирован как выборочный лапласиан гауссианы с пространственным размером, соответствующим потребностям конкретного приложения, как контролируемым его дисперсией. Мономы, которые являются нелинейными операторами, также могут быть реализованы с использованием аналогичного подхода реконструкции и аппроксимации при условии, что сигнал достаточно передискретизирован. Таким образом, такие нелинейные операторы, как, например, тензор структуры и обобщенный тензор структуры , которые используются в распознавании образов для их общей оптимальности наименьших квадратов при оценке ориентации, могут быть реализованы.${\displaystyle K}$${\displaystyle f}$${\displaystyle f_{k}}$${\displaystyle n}$${\displaystyle {\bar {r}}}$${\displaystyle n}$

Спектр дискретного лапласиана на бесконечной сетке представляет ключевой интерес; поскольку это самосопряженный оператор , он имеет действительный спектр. Для соглашения о спектр лежит внутри (так как усредняющий оператор имеет спектральные значения в ). Это также можно увидеть, применив преобразование Фурье. Обратите внимание, что дискретный лапласиан на бесконечной сетке имеет чисто абсолютно непрерывный спектр и, следовательно, не имеет собственных значений или собственных функций.${\displaystyle \Delta =I-M}$${\displaystyle Z}$${\displaystyle [0,2]}$${\displaystyle [-1,1]}$

Если граф представляет собой бесконечную квадратную решетку , то можно показать, что это определение лапласиана соответствует непрерывному лапласиану в пределе бесконечно мелкой сетки. Так, например, на одномерной сетке мы имеем

${\displaystyle {\frac {\partial ^{2}F}{\partial x^{2}}}=\lim _{\epsilon \rightarrow 0}{\frac {[F(x+\epsilon )-F(x)]-[F(x)-F(x-\epsilon )]}{\epsilon ^{2}}}.}$

Это определение лапласиана обычно используется в численном анализе и в обработке изображений . В обработке изображений он считается типом цифрового фильтра , а точнее, краевым фильтром , называемым фильтром Лапласа .

Предположим, описывает распределение температуры по графу , где - температура в вершине . Согласно закону охлаждения Ньютона , тепло, передаваемое от узла к узлу, пропорционально , ​​если узлы и соединены (если они не соединены, тепло не передается). Тогда для теплопроводности ,${\textstyle \phi }$${\textstyle \phi _{i}}$${\textstyle i}$${\textstyle i}$${\textstyle j}$${\textstyle \phi _{i}-\phi _{j}}$${\textstyle i}$${\textstyle j}$${\textstyle k}$

${\displaystyle {\begin{aligned}{\frac {d\phi _{i}}{dt}}&=-k\sum _{j}A_{ij}\left(\phi _{i}-\phi _{j}\right)\\&=-k\left(\phi _{i}\sum _{j}A_{ij}-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\left(\phi _{i}\ \deg(v_{i})-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\sum _{j}\left(\delta _{ij}\ \deg(v_{i})-A_{ij}\right)\phi _{j}\\&=-k\sum _{j}\left(L_{ij}\right)\phi _{j}.\end{aligned}}}$

В матрично-векторной записи,

${\displaystyle {\begin{aligned}{\frac {d\phi }{dt}}&=-k(D-A)\phi \\&=-kL\phi ,\end{aligned}}}$

что дает

${\displaystyle {\frac {d\phi }{dt}}+kL\phi =0.}$

Обратите внимание, что это уравнение имеет ту же форму, что и уравнение теплопроводности , где матрица − L заменяет оператор Лапласа ; отсюда и «графический Лапласиан».${\textstyle \nabla ^{2}}$

Чтобы найти решение этого дифференциального уравнения, применим стандартные методы решения матричного дифференциального уравнения первого порядка . То есть запишем как линейную комбинацию собственных векторов L (так что ) с зависящими от времени коэффициентами,${\textstyle \phi }$${\textstyle \mathbf {v} _{i}}$${\textstyle L\mathbf {v} _{i}=\lambda _{i}\mathbf {v} _{i}}$${\textstyle \phi (t)=\sum _{i}c_{i}(t)\mathbf {v} _{i}.}$

Подставляем в исходное выражение (поскольку L — симметричная матрица, ее собственные векторы единичной нормы ортогональны):${\textstyle \mathbf {v} _{i}}$

${\displaystyle {\begin{aligned}0={}&{\frac {d\left(\sum _{i}c_{i}(t)\mathbf {v} _{i}\right)}{dt}}+kL\left(\sum _{i}c_{i}(t)\mathbf {v} _{i}\right)\\{}={}&\sum _{i}\left[{\frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)L\mathbf {v} _{i}\right]\\{}={}&\sum _{i}\left[{\frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)\lambda _{i}\mathbf {v} _{i}\right]\\\Rightarrow 0={}&{\frac {dc_{i}(t)}{dt}}+k\lambda _{i}c_{i}(t),\\\end{aligned}}}$

чье решение

${\displaystyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}.}$

Как было показано ранее, собственные значения L неотрицательны, что показывает, что решение уравнения диффузии приближается к равновесию, поскольку оно только экспоненциально затухает или остается постоянным. Это также показывает, что при заданном и начальном условии решение в любой момент времени t может быть найдено. ^[12]${\textstyle \lambda _{i}}$${\textstyle \lambda _{i}}$${\textstyle c_{i}(0)}$

Чтобы найти для каждого из них в терминах общего начального условия , просто спроецируйте на собственные векторы единичной нормы ;${\textstyle c_{i}(0)}$${\textstyle i}$${\textstyle \phi (0)}$${\textstyle \phi (0)}$${\textstyle \mathbf {v} _{i}}$

${\displaystyle c_{i}(0)=\left\langle \phi (0),\mathbf {v} _{i}\right\rangle }$.

Этот подход был применен для количественного моделирования теплопередачи на неструктурированных сетках. ^{[13] [14]}

В случае неориентированных графов это работает, поскольку симметрично, и по спектральной теореме его собственные векторы все ортогональны. Таким образом, проекция на собственные векторы является просто ортогональным преобразованием координат начального условия в набор координат, которые экспоненциально затухают и не зависят друг от друга.${\textstyle L}$${\textstyle L}$

Для понимания , единственные термины , которые остаются, это те, где , поскольку${\textstyle \lim _{t\to \infty }\phi (t)}$${\textstyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}}$${\textstyle \lambda _{i}=0}$

${\displaystyle \lim _{t\to \infty }e^{-k\lambda _{i}t}={\begin{cases}0,&{\text{if}}&\lambda _{i}>0\\1,&{\text{if}}&\lambda _{i}=0\end{cases}}}$

Другими словами , равновесное состояние системы полностью определяется ядром .${\textstyle L}$

Поскольку по определению, вектор всех единиц находится в ядре. Если в графе есть непересекающиеся связные компоненты , то этот вектор всех единиц можно разбить на сумму независимых собственных векторов единиц и нулей, где каждый связный компонент соответствует собственному вектору с единицами в элементах связного компонента и нулями в других местах.${\textstyle \sum _{j}L_{ij}=0}$${\textstyle \mathbf {v} ^{1}}$${\textstyle k}$${\textstyle k}$${\textstyle \lambda =0}$

Следствием этого является то, что при заданном начальном условии для графа с вершинами${\textstyle c(0)}$${\textstyle N}$

${\displaystyle \lim _{t\to \infty }\phi (t)=\left\langle c(0),\mathbf {v^{1}} \right\rangle \mathbf {v^{1}} }$

где

${\displaystyle \mathbf {v^{1}} ={\frac {1}{\sqrt {N}}}[1,1,\ldots ,1]}$

Для каждого элемента , т.е. для каждой вершины графа, его можно переписать как${\textstyle \phi _{j}}$${\textstyle \phi }$${\textstyle j}$

${\displaystyle \lim _{t\to \infty }\phi _{j}(t)={\frac {1}{N}}\sum _{i=1}^{N}c_{i}(0)}$.

Другими словами, в устойчивом состоянии значение сходится к одному и тому же значению в каждой из вершин графа, что является средним значением начальных значений во всех вершинах. Поскольку это решение уравнения диффузии тепла, это интуитивно понятно. Мы ожидаем, что соседние элементы в графе будут обмениваться энергией до тех пор, пока эта энергия не распределится равномерно по всем элементам, которые соединены друг с другом.${\textstyle \phi }$

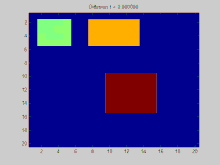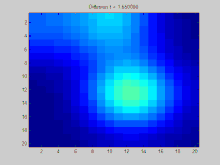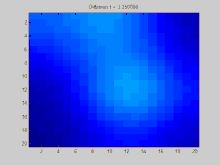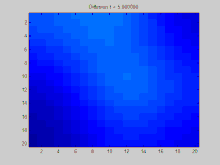
В этом разделе показан пример функции, распространяющейся со временем через график. График в этом примере построен на двумерной дискретной сетке, точки которой соединены с восемью соседями. Три начальные точки указаны как имеющие положительное значение, в то время как остальные значения в сетке равны нулю. Со временем экспоненциальное убывание действует, чтобы равномерно распределить значения в этих точках по всей сетке.${\textstyle \phi }$

Полный исходный код Matlab, который был использован для генерации этой анимации, представлен ниже. Он показывает процесс задания начальных условий, проецирования этих начальных условий на собственные значения матрицы Лапласа и моделирования экспоненциального затухания этих спроецированных начальных условий.

N = 20 ; % Количество пикселей по измерению изображения A = нули ( N , N ); % Изображение Adj = нули ( N * N , N * N ); % Матрица смежности               % Используем 8 соседей и заполняем матрицу смежности dx = [ - 1 , 0 , 1 , - 1 , 1 , - 1 , 0 , 1 ]; dy = [ - 1 , - 1 , - 1 , 0 , 0 , 1 , 1 , 1 ]; для x = 1 : N для y = 1 : N index = ( x - 1 ) * N + y ; для ne = 1 : length ( dx ) newx = x + dx ( ne ); newy = y + dy ( ne ); if newx > 0 && newx <= N && newy > 0 && newy <= N index2 = ( newx - 1 ) * N + newy ; Adj ( index , index2 ) = 1 ; end end end end                                                                                      % НИЖЕ ПРИВЕДЕН КЛЮЧЕВОЙ КОД, КОТОРЫЙ ВЫЧИСЛЯЕТ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Deg = diag ( sum ( Adj , 2 )); % Вычислить матрицу степеней L = Deg - Adj ; % Вычислить матрицу Лапласа через матрицы степеней и смежности [ V , D ] = eig ( L ); % Вычислить собственные значения/векторы матрицы Лапласа D = diag ( D );               % Начальное условие (разместите несколько больших положительных значений вокруг и % сделайте все остальное нулями) C0 = нули ( N , N ) ; C0 ( 2 : 5 , 2 : 5 ) = 5 ; C0 ( 10:15 , 10:15 ) = 10 ; C0 ( 2 : 5 , 8:13 ) = 7 ; C0 = C0 ( :) ;              C0V = V '* C0 ; % Преобразовать начальное условие в систему координат % собственных векторов для t = 0 : 0.05 : 5 % Пройтись по временам и рассчитать затухание каждого начального компонента Phi = C0V .* exp ( - D * t ); % Экспоненциальное затухание для каждого компонента Phi = V * Phi ; % Преобразовать из системы координат собственного вектора в исходную систему координат Phi = reshape ( Phi , N , N ); % Отобразить результаты и записать в файл GIF imagesc ( Phi ); caxis ( [ 0 , 10 ]); title ( sprintf ( ' Diffusion t = %3f' , t )); frame = getframe ( 1 ); im = frame2im ( frame ); [ imind , cm ] = rgb2ind ( im , 256 ); если t == 0 imwrite ( imind , cm , 'out.gif' , 'gif' , 'Loopcount' , inf , 'DelayTime' , 0.1 ); иначе imwrite ( imind , cm , 'out.gif' , 'gif' , 'WriteMode' , 'append' , 'DelayTime' , 0.1 ); конец конец                                                                  

Пусть — потенциальная функция, определенная на графике. Обратите внимание, что P можно рассматривать как мультипликативный оператор, действующий диагонально на${\displaystyle P\colon V\rightarrow R}$${\displaystyle \phi }$

${\displaystyle (P\phi )(v)=P(v)\phi (v).}$

Тогда — дискретный оператор Шредингера , аналог непрерывного оператора Шредингера .${\displaystyle H=\Delta +P}$

Если число ребер, сходящихся в вершине, равномерно ограничено, а потенциал ограничен, то H ограничен и самосопряжен .

Спектральные свойства этого гамильтониана можно изучить с помощью теоремы Стоуна ; это является следствием двойственности между частично упорядоченными множествами и булевыми алгебрами .

На регулярных решетках оператор обычно имеет как решения в виде бегущей волны, так и локализованные решения Андерсона, в зависимости от того, является ли потенциал периодическим или случайным.

Функция Грина дискретного оператора Шредингера в резольвентном формализме задается выражением

${\displaystyle G(v,w;\lambda )=\left\langle \delta _{v}\left|{\frac {1}{H-\lambda }}\right|\delta _{w}\right\rangle }$

где подразумевается дельта-функция Кронекера на графике: ; то есть она равна 1 , если v = w , и 0 в противном случае.${\displaystyle \delta _{w}}$${\displaystyle \delta _{w}(v)=\delta _{wv}}$

Для фиксированного и комплексного числа функция Грина, рассматриваемая как функция v, является единственным решением${\displaystyle w\in V}$${\displaystyle \lambda }$

${\displaystyle (H-\lambda )G(v,w;\lambda )=\delta _{w}(v).}$

Некоторые уравнения, включающие дискретный Лапласиан, имеют решения только на просто-сшитых диаграммах Дынкина (все ребра кратности 1) и являются примером классификации ADE . В частности, единственные положительные решения однородного уравнения:

${\displaystyle \Delta \phi =\phi ,}$

словами,

«Удвоенная любая метка равна сумме меток на соседних вершинах».

находятся на расширенных (аффинных) диаграммах ADE Dynkin, из которых есть 2 бесконечных семейства (A и D) и 3 исключения (E). Полученная нумерация уникальна вплоть до масштаба, и если наименьшее значение установлено равным 1, остальные числа являются целыми числами, в диапазоне до 6.

Обычные графы ADE являются единственными графами, допускающими положительную маркировку со следующим свойством:

Удвоенная любая метка минус два равна сумме меток на соседних вершинах.

В терминах Лапласа положительные решения неоднородного уравнения:

${\displaystyle \Delta \phi =\phi -2.}$

Полученная нумерация уникальна (масштаб указан цифрой «2») и состоит из целых чисел; для E ₈ они варьируются от 58 до 270 и наблюдались еще в 1968 году. ^[15]

• Анализ формы спектра
• Электрическая сеть
• Сумма Кронекера дискретных лапласианов
• Дискретное исчисление

• Оливье, Ян (2004). "Спектральный зазор графа". Архивировано из оригинала 2007-05-23.