Центральная схема разности

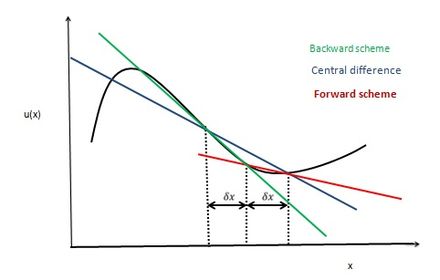
Рисунок 1. Сравнение различных схем

В прикладной математике схема центральной разности представляет собой метод конечных разностей , который оптимизирует приближение для дифференциального оператора в центральном узле рассматриваемого участка и обеспечивает численные решения дифференциальных уравнений. [1] Это одна из схем, используемых для решения интегрированного уравнения конвекции-диффузии и вычисления переносимого свойства Φ на гранях e и w, где e и w являются сокращениями для востока и запада (направления компаса обычно используются для указания направлений на вычислительных сетках). Преимущества метода заключаются в том, что его легко понять и реализовать, по крайней мере, для простых материальных отношений; и что его скорость сходимости выше, чем у некоторых других методов конечной разности, таких как прямое и обратное разность. Правая часть уравнения конвекции-диффузии, которая в основном выделяет члены диффузии, может быть представлена ​​с помощью приближения центральной разности. Чтобы упростить решение и анализ, можно логически использовать линейную интерполяцию для вычисления значений граней ячеек для левой части этого уравнения, которая представляет собой не что иное, как конвективные члены. Таким образом, номинальные значения ячеек свойства для равномерной сетки можно записать в виде: [2]

Ф е = 1 2 ( Ф П + Ф Э ) {\displaystyle \Phi _{e}={\tfrac {1}{2}}(\Phi _{P}+\Phi _{E})} Ф ж = 1 2 ( Ф Вт + Ф П ) {\displaystyle \Phi _{w}={\tfrac {1}{2}}(\Phi _{W}+\Phi _{P})}

Уравнение стационарной конвекции-диффузии

Уравнение конвекции-диффузии является коллективным представлением уравнений диффузии и конвекции и описывает или объясняет каждое физическое явление, включающее конвекцию и диффузию при переносе частиц, энергии и других физических величин внутри физической системы: [2]

див ⁡ ( ρ ты φ ) = див ⁡ ( Г ∇ φ ) + С φ ; {\displaystyle \operatorname {div} (\rho u\varphi) = \operatorname {div} (\Gamma \nabla \varphi)+S_ {\varphi};\,} где Г — коэффициент диффузии , а Φ — свойство .

Формулировка уравнения стационарной конвекции-диффузии

Формальное интегрирование уравнения стационарной конвекции-диффузии по контрольному объему дает

∫ А н ⋅ ( ρ ты φ ) г А = ∫ А н ⋅ ( Г ∇ φ ) г А + ∫ С В С φ г В {\displaystyle \int _{A}\,n\cdot (\rho u\varphi )\,dA=\int _{A}\,n\cdot (\Gamma \nabla \varphi )\,dA+\int _{CV}\,S_{\varphi }\,dV} (Уравнение 1 )

Это уравнение представляет собой баланс потока в контрольном объеме. Левая сторона дает чистый конвективный поток, а правая сторона содержит чистый диффузионный поток и генерацию или разрушение свойства в контрольном объеме.

При отсутствии уравнения исходного члена получается

d d x ( ρ u φ ) = d d x ( d φ d x ) {\displaystyle {\frac {d}{dx}}(\rho u\varphi )={\frac {d}{dx}}\left({\frac {d\varphi }{dx}}\right)} (Уравнение 2 )

Уравнение непрерывности :

d d x ( ρ u ) = 0 {\displaystyle {d \over dx}(\rho u)=0} (Уравнение 3 )
Рисунок 2. Метод интерполяции

Предполагая контрольный объем и интегрируя уравнение 2 по контрольному объему, получаем:

( ρ u φ A ) e − ( ρ u φ A ) w = ( Γ A d φ / d x ) e − ( Γ A d φ / d x ) w {\displaystyle (\rho u\varphi A)_{e}-(\rho u\varphi A)_{w}=(\Gamma Ad\varphi /dx)_{e}-(\Gamma Ad\varphi /dx)_{w}} (Интегральное уравнение конвекции-диффузии)

Интеграция уравнения 3 дает:

( ρ u A ) e − ( ρ u A ) w = 0 {\displaystyle (\rho uA)_{e}-(\rho uA)_{w}=0} (Комплексное уравнение непрерывности)

Удобно определить две переменные, представляющие конвективный поток массы на единицу площади и диффузионную проводимость на гранях ячеек, например: F = ρ u {\displaystyle F=\rho u} D = Γ / δ x {\displaystyle D=\Gamma /\delta x}

Предполагая , что мы можем записать интегральное уравнение конвекции-диффузии в виде: A e = A w {\displaystyle A_{e}=A_{w}} F e φ e − F w φ w = D e ( φ E − φ P ) − D w ( φ P − φ W ) {\displaystyle F_{e}\varphi _{e}-F_{w}\varphi _{w}=D_{e}(\varphi _{E}-\varphi _{P})-D_{w}(\varphi _{P}-\varphi _{W})}

И интегрированное уравнение непрерывности как: F e − F w = 0 {\displaystyle F_{e}-F_{w}=0}

В центральной схеме разностных уравнений мы пробуем линейную интерполяцию для вычисления номинальных значений ячеек для конвективных условий.

Для равномерной сетки мы можем записать номинальные значения ячеек свойства Φ как φ e = 1 2 ( φ E + φ P ) , φ w = 1 2 ( φ P + φ W ) {\displaystyle \varphi _{e}={\tfrac {1}{2}}(\varphi _{E}+\varphi _{P}),\quad \varphi _{w}={\tfrac {1}{2}}(\varphi _{P}+\varphi _{W})}

Подставляя это в интегральное уравнение конвекции-диффузии, получаем: F e φ E + φ P 2 − F w φ W + φ P 2 = D e ( φ E − φ P ) − D w ( φ P − φ W ) {\displaystyle F_{e}{\frac {\varphi _{E}+\varphi _{P}}{2}}-F_{w}{\frac {\varphi _{W}+\varphi _{P}}{2}}=D_{e}(\varphi _{E}-\varphi _{P})-D_{w}(\varphi _{P}-\varphi _{W})}

И по поводу перестановки: [ ( D w + F w 2 ) + ( D e − F e 2 ) + ( F e − F w ) ] φ P = ( D w + F w 2 ) φ W + ( D e − F e 2 ) φ E {\displaystyle \left[\left(D_{w}+{\frac {F_{w}}{2}}\right)+\left(D_{e}-{\frac {F_{e}}{2}}\right)+(F_{e}-F_{w})\right]\varphi _{P}=\left(D_{w}+{\frac {F_{w}}{2}}\right)\varphi _{W}+\left(D_{e}-{\frac {F_{e}}{2}}\right)\varphi _{E}} a P φ P = a W φ W + a E φ E {\displaystyle a_{P}\varphi _{P}=a_{W}\varphi _{W}+a_{E}\varphi _{E}}

Различные аспекты центральной дифференциальной схемы

Консервативность

Сохранение обеспечивается в схеме центрального дифференцирования, поскольку общий баланс потока получается путем суммирования чистого потока через каждый контрольный объем с учетом граничных потоков для контрольных объемов вокруг узлов 1 и 4.

Рисунок 3. Типичная иллюстрация

Граничный поток для контрольного объема вокруг узлов 1 и 4, поскольку [ Γ e 1 ( φ 2 − φ 1 ) δ x − q A ] + [ Γ e 2 ( φ 3 − φ 2 ) δ x − Γ w 2 ( φ 2 − φ 1 ) δ x ] + [ Γ e 3 ( φ 4 − φ 3 ) δ x − Γ w 3 ( φ 3 − φ 2 ) δ x ] + [ q B − Γ w 4 ( φ 4 − φ 3 ) δ x ] = q B − q A {\displaystyle {\begin{aligned}&\left[{\frac {\Gamma _{e_{1}}(\varphi _{2}-\varphi _{1})}{\delta x}}-q_{A}\right]+\left[{\frac {\Gamma _{e_{2}}(\varphi _{3}-\varphi _{2})}{\delta x}}-{\frac {\Gamma _{w_{2}}(\varphi _{2}-\varphi _{1})}{\delta x}}\right]\\[10pt]+{}&\left[{\frac {\Gamma _{e_{3}}(\varphi _{4}-\varphi _{3})}{\delta x}}-{\frac {\Gamma _{w_{3}}(\varphi _{3}-\varphi _{2})}{\delta x}}\right]+\left[q_{B}-{\frac {\Gamma _{w_{4}}(\varphi _{4}-\varphi _{3})}{\delta x}}\right]=q_{B}-q_{A}\end{aligned}}} Γ e 1 = Γ w 2 , Γ e 2 = Γ w 3 , Γ e 3 = Γ w 4 {\displaystyle \Gamma _{e_{1}}=\Gamma _{w_{2}},\Gamma _{e_{2}}=\Gamma _{w_{3}},\Gamma _{e_{3}}=\Gamma _{w_{4}}}

Ограниченность

Центральная разностная схема удовлетворяет первому условию ограниченности .

Так как из уравнения непрерывности следует, то; F e − F w = 0 {\displaystyle F_{e}-F_{w}=0} a P φ P = a W φ W + a E φ E {\displaystyle a_{P}\varphi _{P}=a_{W}\varphi _{W}+a_{E}\varphi _{E}}

Другим существенным требованием для ограниченности является то, что все коэффициенты дискретизированных уравнений должны иметь одинаковый знак (обычно все положительные). Но это выполняется только тогда, когда ( число Пекле ), поскольку для однонаправленного потока ( ) всегда положительно, если F e / D e < 2 {\displaystyle F_{e}/D_{e}<2} F e > 0 , F w > 0 {\displaystyle F_{e}>0,F_{w}>0} a E = ( D e − F e / 2 ) {\displaystyle a_{E}=(D_{e}-F_{e}/2)} D e > F e / 2 {\displaystyle D_{e}>F_{e}/2}

Транспортабельность

Это требует, чтобы транспортабельность изменялась в соответствии с величиной числа Пекле, т.е. когда pe равно нулю, она распространяется во всех направлениях одинаково, а когда Pe увеличивается (конвекция > диффузия) в точке в значительной степени зависит от значения вверх по течению и в меньшей степени от значения вниз по течению. Но схема центральных разностей не обладает транспортабельностью при более высоких pe, поскольку Φ в точке является средним значением соседних узлов для всех Pe. φ {\displaystyle \varphi } φ {\displaystyle \varphi }

Точность

Ошибка усечения ряда Тейлора центральной разностной схемы имеет второй порядок. Центральная разностная схема будет точной только при Pe < 2. Из-за этого ограничения центральная разностная схема не является подходящей практикой дискретизации для общих расчетов потоков.

Применение центральных схем разностной обработки

Преимущества

  • Проще в программировании, требует меньше машинного времени на шаг и хорошо работает с многосеточными методами ускорения
  • Имеет свободный параметр в сочетании с диссипацией четвертой разности, которая необходима для приближения к устойчивому состоянию.
  • Более точная, чем схема первого порядка против потока, если число Пекле меньше 2. [3]

Недостатки

  • Несколько более рассеивающий
  • Приводит к колебаниям в решении или расходимости, если локальное число Пекле больше 2. [4]

Смотрите также

Ссылки

  1. ^ Вычислительная гидродинамика –T CHUNG, ISBN  0-521-59416-2
  2. ^ ab Введение в вычислительную гидродинамику Х.К. ВЕРСТИГА и В. МАЛАЛАСЕКЕРЫ, ISBN 0-582-21884-5 
  3. ^ ab Liu, Xu-Dong; Tadmor, Eitan (1998). "Неколебательная центральная схема третьего порядка для гиперболических законов сохранения". Numerische Mathematik . 79 (3): 397–425. CiteSeerX 10.1.1.26.4631 . doi :10.1007/s002110050345. S2CID  16702600. 
  4. ^ Лекция 5 - Методы решения

Дальнейшее чтение

  • Вычислительная гидродинамика: основы и приложения – Джон Д. Андерсон, ISBN 0-07-001685-2 
  • Вычислительная гидродинамика, том 1 – Клаус А. Хоффманн, Стив Т. Чианг, ISBN 0-9623731-0-9 
  • Одномерная_устойчивая_конвекция_и_диффузия#центральная_разностная_схема
  • Конечные разности
  • Методы центральных различий Архивировано 5 ноября 2013 г. на Wayback Machine
  • Консервативная конечно-разностная схема для уравнений Пуассона–Нернста–Планка
Retrieved from "https://en.wikipedia.org/w/index.php?title=Central_differencing_scheme&oldid=1186436860"