Угловой момент импульса
| Угловой момент импульса | |
|---|---|
 Этот гироскоп сохраняет вертикальное положение во время вращения благодаря сохранению момента импульса. | |
Общие символы | Л |
| В основных единицах СИ | кг⋅м 2 ⋅с −1 |
| Сохранено ? | да |
Выводы из других величин | L = I ω = r × p |
| Измерение | |
| Часть серии статей о |
| Классическая механика |
|---|
Угловой момент (иногда называемый моментом импульса или вращательным моментом ) является вращательным аналогом линейного импульса . Это важная физическая величина , поскольку она является сохраняющейся величиной — полный угловой момент замкнутой системы остается постоянным. Угловой момент имеет как направление , так и величину, и оба они сохраняются. Велосипеды и мотоциклы , летающие диски , [1] нарезные пули и гироскопы обязаны своими полезными свойствами сохранению углового момента. Сохранение углового момента также является причиной того, что ураганы [2] образуют спирали, а нейтронные звезды имеют высокие скорости вращения. В общем случае сохранение ограничивает возможное движение системы, но не определяет его однозначно.
Трехмерный момент импульса для точечной частицы классически представляется как псевдовектор r × p , векторное произведение вектора положения частицы r (относительно некоторого начала координат) и ее вектора импульса ; последний равен p = m v в ньютоновской механике . В отличие от линейного импульса, момент импульса зависит от того, где выбрано это начало координат, поскольку положение частицы измеряется от него.
Угловой момент — это экстенсивная величина ; то есть полный угловой момент любой составной системы — это сумма угловых моментов ее составных частей. Для непрерывного твердого тела или жидкости полный угловой момент — это объемный интеграл плотности углового момента (угловой момент на единицу объема в пределе, когда объем уменьшается до нуля) по всему телу.
Подобно сохранению линейного импульса, где он сохраняется, если нет внешней силы, угловой момент сохраняется, если нет внешнего крутящего момента . Крутящий момент можно определить как скорость изменения углового момента, аналогично силе . Чистый внешний крутящий момент в любой системе всегда равен полному крутящему моменту в системе; сумма всех внутренних крутящих моментов любой системы всегда равна 0 (это вращательный аналог третьего закона движения Ньютона ). Следовательно, для замкнутой системы (где нет чистого внешнего крутящего момента), полный крутящий момент в системе должен быть равен 0, что означает, что полный угловой момент системы постоянен.
Изменение момента импульса при определенном взаимодействии называется угловым импульсом , иногда вращением . [3] Угловой импульс является угловым аналогом (линейного) импульса .
Примеры
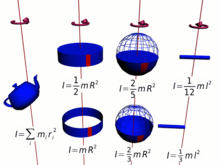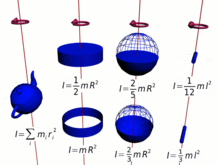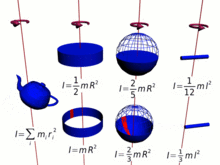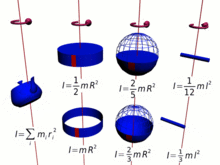
Тривиальный случай момента импульса тела на орбите определяется выражением, где — масса движущегося по орбите объекта, — частота орбиты , а — радиус орбиты.
Вместо этого момент импульса однородной жесткой сферы, вращающейся вокруг своей оси, определяется выражением
где — масса сферы, — частота вращения, — радиус сферы.
Так, например, орбитальный момент импульса Земли относительно Солнца составляет около 2,66 × 10 40 кг⋅м 2 ⋅с −1 , тогда как ее вращательный момент импульса составляет около 7,05 × 10 33 кг⋅м 2 ⋅с −1 .
В случае однородной жесткой сферы, вращающейся вокруг своей оси, если вместо ее массы известна ее плотность , момент импульса определяется выражением
где — плотность сферы , — частота вращения, — радиус сферы.
В простейшем случае вращающегося диска момент импульса определяется выражением [4]
где — масса диска, — частота вращения, — радиус диска.
Если вместо этого диск вращается вокруг своего диаметра (например, подбрасывая монету), его угловой момент определяется выражением [4]
Определение в классической механике
Так же, как и для угловой скорости , существует два особых типа углового момента объекта: спиновый угловой момент — это угловой момент относительно центра масс объекта , в то время как орбитальный угловой момент — это угловой момент относительно выбранного центра вращения. Земля имеет орбитальный угловой момент по природе вращения вокруг Солнца и спиновый угловой момент по природе своего суточного вращения вокруг полярной оси. Полный угловой момент — это сумма спинового и орбитального угловых моментов. В случае Земли первичной сохраняющейся величиной является полный угловой момент Солнечной системы, поскольку угловой момент обменивается в небольшой, но важной степени между планетами и Солнцем. Вектор орбитального углового момента точечной частицы всегда параллелен и прямо пропорционален ее вектору орбитальной угловой скорости ω , где константа пропорциональности зависит как от массы частицы, так и от ее расстояния от начала координат. Вектор момента импульса спина твердого тела пропорционален, но не всегда параллелен вектору угловой скорости спина Ω , что делает константу пропорциональности тензором второго ранга , а не скаляром.
Орбитальный угловой момент в двух измерениях

Угловой момент — это векторная величина (точнее, псевдовектор ), которая представляет собой произведение инерции вращения тела и скорости вращения (в радианах/сек) вокруг определенной оси. Однако, если траектория частицы лежит в одной плоскости , достаточно отбросить векторную природу углового момента и рассматривать его как скаляр (точнее, псевдоскаляр ). [5] Угловой момент можно считать вращательным аналогом линейного импульса. Таким образом, где линейный импульс p пропорционален массе m и линейной скорости v , p = m v , {\displaystyle p=mv,}
Угловой момент L пропорционален моменту инерции I и угловой скорости ω, измеряемой в радианах в секунду. [6] L = I ω . {\displaystyle L=I\omega .}
В отличие от массы, которая зависит только от количества материи, момент инерции зависит также от положения оси вращения и распределения материи. В отличие от линейной скорости, которая не зависит от выбора начала координат, орбитальная угловая скорость всегда измеряется относительно фиксированного начала координат. Поэтому, строго говоря, L следует называть моментом импульса относительно этого центра . [7]
В случае кругового движения отдельной частицы мы можем использовать и для расширения углового момента, сводя его к:
произведение радиуса вращения r на импульс частицы , где - линейная (тангенциальная) скорость .
Этот простой анализ можно применить и к некруговому движению, если использовать компонент движения, перпендикулярный радиус -вектору :
где - перпендикулярная составляющая движения. Расширяя, перестраивая и уменьшая, угловой момент также можно выразить,
где - длина плеча момента , линия, опущенная перпендикулярно из начала координат на путь частицы. Именно это определение, (длина плеча момента) × (линейный импульс) , относится к термину момент импульса . [8]
Скалярный угловой момент из механики Лагранжа
Другой подход заключается в определении углового момента как сопряженного импульса (также называемого каноническим импульсом ) угловой координаты, выраженной в лагранжиане механической системы. Рассмотрим механическую систему с массой, вынужденной двигаться по окружности радиусом в отсутствие какого-либо внешнего силового поля. Кинетическая энергия системы равна T = 1 2 m r 2 ω 2 = 1 2 m r 2 ϕ ˙ 2 . {\displaystyle T={\tfrac {1}{2}}mr^{2}\omega ^{2}={\tfrac {1}{2}}mr^{2}{\dot {\phi }}^{2}.}
А потенциальная энергия равна
Тогда лагранжиан равен
Обобщенный импульс, «канонически сопряженный» с координатой, определяется как
Орбитальный угловой момент в трех измерениях

Чтобы полностью определить орбитальный угловой момент в трех измерениях , необходимо знать скорость, с которой вектор положения выметает угол, направление, перпендикулярное мгновенной плоскости углового смещения, и вовлеченную массу , а также то, как эта масса распределена в пространстве. [9] Сохраняя эту векторную природу углового момента, общая природа уравнений также сохраняется и может описывать любой вид трехмерного движения вокруг центра вращения — кругового , линейного или иного. В векторной записи орбитальный угловой момент точечной частицы, движущейся вокруг начала координат, можно выразить как: где
- - момент инерции точечной массы ,
- ω = r × v r 2 {\displaystyle {\boldsymbol {\omega }}={\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}} — орбитальная угловая скорость частицы вокруг начала координат,
- — вектор положения частицы относительно начала координат, а ,
- — линейная скорость частицы относительно начала координат, а
- масса частицы.
Это можно расширить, сократить и по правилам векторной алгебры переставить: что является векторным произведением вектора положения и линейного импульса частицы. По определению векторного произведения вектор перпендикулярен обоим и . Он направлен перпендикулярно плоскости углового смещения, как указано в правиле правой руки – так что угловая скорость рассматривается как направленная против часовой стрелки от головы вектора. Наоборот, вектор определяет плоскость, в которой лежат и .
Определяя единичный вектор, перпендикулярный плоскости углового перемещения, получаем скалярную угловую скорость , где и где — перпендикулярная составляющая движения, как и выше.
Таким образом, двумерным скалярным уравнениям предыдущего раздела можно задать направление: и для кругового движения, где все движение перпендикулярно радиусу .
В сферической системе координат вектор момента импульса выражается как
Аналогия с линейным импульсом
Угловой момент можно описать как вращательный аналог линейного импульса . Как и линейный импульс, он включает элементы массы и смещения . В отличие от линейного импульса он также включает элементы положения и формы .
Многие проблемы в физике включают материю в движении относительно некоторой определенной точки пространства, будь то фактическое вращение вокруг нее или просто движение мимо нее, где желательно знать, какое влияние движущаяся материя оказывает на точку — может ли она оказывать на нее энергию или выполнять работу относительно нее? Энергия , способность выполнять работу , может быть сохранена в материи путем приведения ее в движение — сочетание ее инерции и ее смещения. Инерция измеряется ее массой , а смещение — ее скоростью . Их произведение,
есть импульс материи . [10] Отнесение этого импульса к центральной точке вносит осложнение: импульс не прикладывается к точке напрямую. Например, частица материи на внешнем крае колеса, по сути, находится на конце рычага той же длины, что и радиус колеса, ее импульс поворачивает рычаг вокруг центральной точки. Этот воображаемый рычаг известен как плечо момента . Он имеет эффект умножения усилия импульса пропорционально его длине, эффект, известный как момент . Следовательно , импульс частицы, отнесенный к определенной точке,
это угловой момент , иногда называемый, как здесь, моментом импульса частицы против этой конкретной центральной точки. Уравнение объединяет момент ( плечо вращающего момента массы ) с линейной (эквивалентной прямой) скоростью . Линейная скорость, отнесенная к центральной точке, является просто произведением расстояния и угловой скорости против точки: еще один момент. Следовательно, угловой момент содержит двойной момент: Немного упрощая, величина является моментом инерции частицы , иногда называемым вторым моментом массы. Это мера вращательной инерции. [11]
Приведенная выше аналогия поступательного и вращательного импульсов может быть выражена в векторной форме: [ необходима ссылка ]
- для линейного движения
- для вращения
Направление импульса связано с направлением скорости линейного движения. Направление момента импульса связано с угловой скоростью вращения.
Поскольку момент инерции является важнейшей частью спинового момента импульса, последний обязательно включает в себя все осложнения первого, который вычисляется путем умножения элементарных частиц массы на квадраты их расстояний от центра вращения. [12] Таким образом, полный момент инерции и момент импульса являются сложной функцией конфигурации материи вокруг центра вращения и ориентации вращения для различных частиц.
Для твердого тела , например, колеса или астероида, ориентация вращения — это просто положение оси вращения относительно материи тела. Она может проходить или не проходить через центр масс , или может полностью лежать вне тела. Для одного и того же тела угловой момент может принимать разное значение для каждой возможной оси, вокруг которой может происходить вращение. [13] Он достигает минимума, когда ось проходит через центр масс. [14]
Для набора объектов, вращающихся вокруг центра, например, всех тел Солнечной системы , ориентации могут быть несколько организованы, как в Солнечной системе, при этом большинство осей тел лежат близко к оси системы. Их ориентации также могут быть совершенно случайными.
Короче говоря, чем больше масса и чем дальше она от центра вращения (чем длиннее плечо момента ), тем больше момент инерции, и, следовательно, больше угловой момент для данной угловой скорости . Во многих случаях момент инерции , а следовательно, и угловой момент, можно упростить следующим образом: [15] I = k 2 m , {\displaystyle I=k^{2}m,} где — радиус инерции , расстояние от оси, на котором вся масса может считаться сосредоточенной.
Аналогично, для точечной массы момент инерции определяется как, где - радиус точечной массы от центра вращения,
и для любого набора частиц как сумма,
Зависимость момента импульса от положения и формы отражается в его единицах измерения в сравнении с линейным импульсом: кг⋅м 2 /с или Н⋅м⋅с для момента импульса в сравнении с кг⋅м/с или Н⋅с для линейного импульса. При вычислении момента импульса как произведения момента инерции на угловую скорость угловая скорость должна быть выражена в радианах в секунду, где радиан принимает безразмерное значение единицы. (При выполнении размерного анализа может быть продуктивным использовать ориентационный анализ , который рассматривает радианы как базовую единицу, но это не делается в Международной системе единиц ). Единицы измерения момента импульса можно интерпретировать как крутящий момент ⋅время. Объект с моментом импульса L Н⋅м⋅с может быть уменьшен до нулевой угловой скорости угловым импульсом L Н⋅м⋅с . [ 16] [17]
Плоскость , перпендикулярная оси момента импульса и проходящая через центр масс [18] , иногда называют неизменной плоскостью , поскольку направление оси остается фиксированным, если рассматривать только взаимодействия тел внутри системы, свободные от внешних влияний. [19] Одной из таких плоскостей является неизменная плоскость Солнечной системы .
Угловой импульс и крутящий момент
Второй закон движения Ньютона можно выразить математически, или сила = масса × ускорение . Вращательный эквивалент для точечных частиц может быть выведен следующим образом: что означает, что крутящий момент (т. е. производная по времени от момента импульса) равен τ = d I d t ω + I d ω d t . {\displaystyle {\boldsymbol {\tau }}={\frac {dI}{dt}}{\boldsymbol {\omega }}+I{\frac {d{\boldsymbol {\omega }}}{dt}}.}
Поскольку момент инерции равен , то отсюда следует, что , и что сводится к
Это вращательный аналог второго закона Ньютона. Обратите внимание, что крутящий момент не обязательно пропорционален или параллелен угловому ускорению (как можно было бы ожидать). Причина этого в том, что момент инерции частицы может меняться со временем, чего не может произойти для обычной массы.
Сохранение момента импульса
.jpg/440px-Cup_of_Russia_2010_-_Yuko_Kawaguti_(2).jpg)
Общие соображения
Вращательный аналог третьего закона движения Ньютона можно записать так: «В замкнутой системе никакой крутящий момент не может быть приложен к какой-либо материи без приложения к какой-либо другой материи равного и противоположного крутящего момента вокруг той же оси». [20] Следовательно, угловой момент может обмениваться между объектами в замкнутой системе, но общий угловой момент до и после обмена остается постоянным (сохраняется). [21]
С другой стороны, вращательный аналог первого закона движения Ньютона можно записать так: «Твердое тело продолжает находиться в состоянии равномерного вращения, если на него не действует внешнее воздействие». [20] Таким образом, при отсутствии внешнего воздействия на него исходный угловой момент системы остается постоянным . [22]
Сохранение момента импульса используется при анализе движения центральной силы . Если результирующая сила, действующая на некоторое тело, всегда направлена к некоторой точке, центру , то крутящий момент на теле относительно центра отсутствует, так как вся сила направлена вдоль радиус -вектора , и ни одна не перпендикулярна радиусу. Математически, крутящий момент , потому что в этом случае и являются параллельными векторами. Следовательно, момент импульса тела относительно центра постоянен. Это имеет место с гравитационным притяжением на орбитах планет и спутников , где гравитационная сила всегда направлена к основному телу, а вращающиеся по орбите тела сохраняют момент импульса, обмениваясь расстоянием и скоростью при движении вокруг основного тела . Движение центральной силы также используется при анализе модели атома Бора .
Для планеты угловой момент распределяется между вращением планеты и ее вращением по орбите, и они часто обмениваются различными механизмами. Сохранение углового момента в системе Земля-Луна приводит к передаче углового момента от Земли к Луне из-за приливного момента, который Луна оказывает на Землю. Это, в свою очередь, приводит к замедлению скорости вращения Земли, примерно на 65,7 наносекунд в день, [23] и к постепенному увеличению радиуса орбиты Луны, примерно на 3,82 сантиметра в год. [24]

Сохранение момента импульса объясняет угловое ускорение фигуриста , когда он приближает свои руки и ноги к вертикальной оси вращения. Приближая часть массы своего тела к оси, он уменьшает момент инерции своего тела. Поскольку момент импульса является произведением момента инерции и угловой скорости , если момент импульса остается постоянным (сохраняется), то угловая скорость (скорость вращения) фигуриста должна увеличиваться.
Это же явление приводит к чрезвычайно быстрому вращению компактных звезд (таких как белые карлики , нейтронные звезды и черные дыры ), когда они образуются из гораздо более крупных и медленно вращающихся звезд.
Сохранение не всегда является полным объяснением динамики системы, но является ключевым ограничением. Например, вращающийся волчок подвержен гравитационному моменту, заставляющему его наклоняться и изменять угловой момент относительно оси нутации , но, пренебрегая трением в точке вращательного контакта, он имеет сохраняющийся угловой момент относительно своей оси вращения и еще один относительно своей оси прецессии . Кроме того, в любой планетной системе планеты, звезды, кометы и астероиды могут двигаться многочисленными сложными способами, но только так, чтобы угловой момент системы сохранялся.
Теорема Нётер утверждает, что каждый закон сохранения связан с симметрией (инвариантом) базовой физики. Симметрия, связанная с сохранением момента импульса, является вращательной инвариантностью . Тот факт, что физика системы не меняется, если она вращается на любой угол вокруг оси, подразумевает, что момент импульса сохраняется. [25]
Связь со вторым законом движения Ньютона
Хотя полное сохранение углового момента можно понимать отдельно от законов движения Ньютона как вытекающее из теоремы Нётер в системах, симметричных относительно вращений, его также можно понимать просто как эффективный метод вычисления результатов, которые также могут быть получены иным образом непосредственно из второго закона Ньютона вместе с законами, управляющими силами природы (такими как третий закон Ньютона, уравнения Максвелла и сила Лоренца ). Действительно, при заданных начальных условиях положения и скорости для каждой точки, а также силах в таком состоянии, можно использовать второй закон Ньютона для вычисления второй производной положения, и решение для этого дает полную информацию о развитии физической системы со временем. [26] Обратите внимание, однако, что это больше не верно в квантовой механике из-за существования спина частицы , который является угловым моментом, который не может быть описан кумулятивным эффектом точечных движений в пространстве.
В качестве примера рассмотрим уменьшение момента инерции , например, когда фигурист тянет руки, ускоряя круговое движение. В терминах сохранения момента импульса, мы имеем для момента импульса L , момента инерции I и угловой скорости ω :
Используя это, мы видим, что изменение требует энергии:
так что уменьшение момента инерции требует вложения энергии.
Это можно сравнить с работой, выполненной с помощью законов Ньютона. Каждая точка вращающегося тела ускоряется в каждый момент времени с радиальным ускорением:
Рассмотрим точку массой m , радиус-вектор которой относительно центра движения перпендикулярен оси z в данный момент времени и находится на расстоянии z . Центростремительная сила , действующая на эту точку, сохраняющая круговое движение, равна:
Таким образом, работа, необходимая для перемещения этой точки на расстояние dz от центра движения, равна:
Для неточечного тела необходимо интегрировать по этому, заменив m на плотность массы на единицу z . Это дает:
что в точности соответствует энергии, необходимой для сохранения момента импульса.
Обратите внимание, что приведенный выше расчет можно также выполнить на основе массы, используя только кинематику . Таким образом, явление ускорения тангенциальной скорости фигуриста при подтягивании рук к себе можно понять следующим образом на языке неспециалиста: ладони фигуриста не движутся по прямой линии, поэтому они постоянно ускоряются внутрь, но не получают дополнительной скорости, поскольку ускорение всегда происходит, когда их движение внутрь равно нулю. Однако это отличается от подтягивания ладоней ближе к телу: ускорение из-за вращения теперь увеличивает скорость; но из-за вращения увеличение скорости не приводит к значительной скорости внутрь, а к увеличению скорости вращения.
Принцип стационарного действия
В классической механике можно показать, что вращательная инвариантность функционалов действия подразумевает сохранение углового момента. Действие определяется в классической физике как функционал положений, часто представляемый с помощью квадратных скобок, и конечного и начального времени. Оно принимает следующую форму в декартовых координатах: где повторяющиеся индексы указывают на суммирование по индексу. Если действие инвариантно относительно бесконечно малого преобразования, его можно математически сформулировать как: .
При преобразовании действие становится:
где мы можем использовать разложение членов до первого порядка по :
давая следующее изменение в действии:
Поскольку все вращения можно выразить в виде матричной экспоненты кососимметричных матриц, т.е. как , где — кососимметричная матрица, а — угол поворота, то можно выразить изменение координат из-за поворота с точностью до первого порядка бесконечно малого угла поворота как:
Объединяя уравнение движения и вращательную инвариантность действия , из приведенных выше уравнений получаем, что: Поскольку это верно для любой матрицы , которая удовлетворяет этому уравнению, то это приводит к сохранению следующей величины:
как . Это соответствует сохранению момента импульса на протяжении всего движения. [27]
Лагранжев формализм
В механике Лагранжа момент импульса вращения вокруг заданной оси — это сопряженный импульс обобщенной координаты угла вокруг той же оси. Например, момент импульса вокруг оси z равен: где — лагранжиан, а — угол вокруг оси z.
Обратите внимание, что , производная угла по времени, является угловой скоростью . Обычно лагранжиан зависит от угловой скорости через кинетическую энергию: Последнюю можно записать, разделив скорость на ее радиальную и тангенциальную части, причем тангенциальная часть в плоскости xy вокруг оси z равна: где индекс i обозначает i-е тело, а m , v T и ω z обозначают массу, тангенциальную скорость вокруг оси z и угловую скорость вокруг этой оси соответственно.
Для тела, не являющегося точечным, с плотностью ρ вместо этого имеем: где интегрирование выполняется по площади тела, [28] а I z — момент инерции вокруг оси z.
Таким образом, предполагая, что потенциальная энергия не зависит от ω z (это предположение может оказаться неверным для электромагнитных систем), имеем момент импульса i-го объекта:
До сих пор мы вращали каждый объект на отдельный угол; мы также можем определить общий угол θ z , на который мы вращаем всю систему, тем самым вращая также каждый объект вокруг оси z, и имеем общий угловой момент:
Из уравнений Эйлера–Лагранжа следует, что:
Поскольку лагранжиан зависит от углов объекта только через потенциал, мы имеем: что представляет собой крутящий момент, действующий на i -й объект.
Предположим, что система инвариантна к вращениям, так что потенциал не зависит от общего вращения на угол θ z (таким образом, он может зависеть от углов объектов только через их разности, в виде ). Поэтому для полного углового момента получаем:
И, таким образом, момент импульса вокруг оси z сохраняется.
Этот анализ можно повторить отдельно для каждой оси, что даст разговор о векторе углового момента. Однако углы вокруг трех осей нельзя рассматривать одновременно как обобщенные координаты, поскольку они не являются независимыми; в частности, двух углов на точку достаточно для определения ее положения. Хотя верно, что в случае твердого тела для его полного описания требуется, в дополнение к трем поступательным степеням свободы, также спецификация трех вращательных степеней свободы; однако их нельзя определить как вращения вокруг декартовых осей (см. углы Эйлера ). Это предостережение отражено в квантовой механике в нетривиальных коммутационных соотношениях различных компонентов оператора углового момента .
Гамильтонов формализм
Эквивалентно, в гамильтоновой механике гамильтониан может быть описан как функция углового момента. Как и прежде, часть кинетической энергии, связанная с вращением вокруг оси z для i -го объекта, равна:
что аналогично зависимости энергии от импульса вдоль оси z, .
Уравнения Гамильтона связывают угол вокруг оси z с его сопряженным импульсом — моментом импульса вокруг той же оси:
Первое уравнение дает
И поэтому мы получаем те же результаты, что и в лагранжевом формализме.
Обратите внимание, что для объединения всех осей мы записываем кинетическую энергию как:
где p r — импульс в радиальном направлении, а момент инерции — трехмерная матрица ; жирные буквы обозначают трехмерные векторы.
Для точечных тел имеем:
Эта форма кинетической энергии гамильтониана полезна при анализе центральных потенциальных задач и легко преобразуется в квантово-механическую рабочую систему (например, в задаче об атоме водорода ).
Угловой момент в орбитальной механике
Хотя в классической механике язык углового момента можно заменить законами движения Ньютона, он особенно полезен для движения в центральном потенциале , например, для движения планет в солнечной системе. Таким образом, орбита планеты в солнечной системе определяется ее энергией, угловым моментом и углами большой оси орбиты относительно системы координат.
В астродинамике и небесной механике величина, тесно связанная с угловым моментом, определяется как [29] называемый удельным угловым моментом . Обратите внимание, что масса часто не важна в расчетах орбитальной механики, поскольку движение тела определяется гравитацией . Основное тело системы часто настолько больше любых тел, движущихся вокруг него, что гравитационным воздействием меньших тел на него можно пренебречь; оно сохраняет, по сути, постоянную скорость. Движение всех тел подвержено его гравитации одинаково, независимо от массы, и поэтому все движутся примерно одинаково в одних и тех же условиях.
Твёрдые тела
Угловой момент также является чрезвычайно полезным понятием для описания вращающихся твердых тел, таких как гироскоп или каменистая планета. Для непрерывного распределения массы с функцией плотности ρ ( r ) дифференциальный элемент объема dV с вектором положения r внутри массы имеет элемент массы dm = ρ ( r ) dV . Следовательно, бесконечно малый угловой момент этого элемента равен:
и интегрирование этого дифференциала по объему всей массы дает ее полный угловой момент:
В следующем выводе интегралы, подобные этому, могут заменить суммы для случая непрерывной массы.
Сбор частиц

Для совокупности частиц, движущихся вокруг произвольного начала координат, информативно разработать уравнение момента импульса, разложив их движение на компоненты вокруг их собственного центра масс и вокруг начала координат. Учитывая,
- масса частицы ,
- - это вектор положения частицы относительно начала координат,
- - скорость частицы относительно начала координат,
- - радиус-вектор центра масс относительно начала координат,
- - скорость центра масс относительно начала координат,
- - радиус-вектор частицы относительно центра масс,
- - скорость частицы относительно центра масс,
Общая масса частиц — это просто их сумма,
Вектор положения центра масс определяется как [30]
По результатам осмотра,
- и
Полный момент импульса совокупности частиц представляет собой сумму моментов импульса каждой частицы,
( 1 )
Расширяясь ,
Расширяясь ,
Можно показать, что (см. боковую панель),
Докажите, что который, по определению центра масс, есть и аналогично для |
- и
поэтому второй и третий члены исчезают,
Первый член можно переставить,
и полный угловой момент для совокупности частиц в конечном итоге равен [31]
( 2 )
Первый член — это угловой момент центра масс относительно начала координат. Подобно § Отдельная частица , ниже, это угловой момент одной частицы массы M в центре масс, движущейся со скоростью V . Второй член — это угловой момент частиц, движущихся относительно центра масс, аналогично § Неподвижный центр масс , ниже. Результат является общим — движение частиц не ограничивается вращением или обращением вокруг начала координат или центра масс. Частицы не обязательно должны быть индивидуальными массами, но могут быть элементами непрерывного распределения, такими как твердое тело.
Перегруппировав уравнение ( 2 ) с помощью векторных тождеств, умножив оба члена на «один» и сгруппировав соответствующим образом,
дает полный момент импульса системы частиц через момент инерции и угловую скорость ,
( 3 )
Случай одной частицы
В случае одиночной частицы, движущейся вокруг произвольного начала координат, уравнения ( 2 ) и ( 3 ) для полного углового момента сводятся к следующему:
Случай неподвижного центра масс
Для случая центра масс, фиксированного в пространстве относительно начала координат, уравнения ( 2 ) и ( 3 ) для полного момента импульса сводятся к следующему:
Угловой момент в общей теории относительности

В современной (20-го века) теоретической физике момент импульса (не включая какой-либо собственный момент импульса – см. ниже) описывается с использованием другого формализма, вместо классического псевдовектора . В этом формализме момент импульса является 2-формой заряда Нётер, связанного с вращательной инвариантностью. В результате момент импульса обычно не сохраняется локально для общих искривленных пространств-времен , если только они не обладают вращательной симметрией; [32] тогда как глобально само понятие момента импульса имеет смысл только в том случае, если пространство-время асимптотически плоское. [33] Если пространство-время имеет только аксиальную симметрию, как для метрики Керра , полный момент импульса не сохраняется, но сохраняется, что связано с инвариантностью вращения вокруг оси симметрии, где обратите внимание, что где – метрика [ необходимо устранение неоднозначности ] , – масса покоя , – 4-скорость , а – 4-позиция в сферических координатах.
В классической механике угловой момент частицы может быть переосмыслен как элемент плоскости: в котором внешнее произведение (∧) заменяет векторное произведение (×) (эти произведения имеют схожие характеристики, но неэквивалентны). Это имеет преимущество более ясной геометрической интерпретации как элемента плоскости, определяемого с помощью векторов x и p , и выражение верно в любом количестве измерений. В декартовых координатах: или более компактно в индексной записи:
Угловая скорость может быть также определена как антисимметричный тензор второго порядка с компонентами ω ij . Связь между двумя антисимметричными тензорами задается моментом инерции, который теперь должен быть тензором четвертого порядка: [34]
Опять же, это уравнение в L и ω как тензорах верно в любом числе измерений. Это уравнение также появляется в формализме геометрической алгебры , в котором L и ω являются бивекторами, а момент инерции является отображением между ними.
В релятивистской механике релятивистский момент импульса частицы выражается как антисимметричный тензор второго порядка: в терминах четырехвекторов , а именно четырехпозиционного X и четырехимпульса P , и поглощает указанный выше L вместе с моментом массы , т. е. произведением релятивистской массы частицы и ее центра масс , которое можно рассматривать как описание движения ее центра масс, поскольку масса-энергия сохраняется.
В каждом из вышеперечисленных случаев для системы частиц полный момент импульса представляет собой просто сумму моментов импульса отдельных частиц, а центр масс — для системы.
Угловой момент в квантовой механике
В квантовой механике угловой момент (как и другие величины) выражается как оператор , а его одномерные проекции имеют квантованные собственные значения . Угловой момент подчиняется принципу неопределенности Гейзенберга , подразумевающему, что в любой момент времени только одна проекция (также называемая «компонентом») может быть измерена с определенной точностью; остальные две остаются неопределенными. Из-за этого ось вращения квантовой частицы не определена. Квантовые частицы обладают типом неорбитального углового момента, называемого «спин», но этот угловой момент не соответствует вращательному движению. [35] В релятивистской квантовой механике приведенное выше релятивистское определение становится тензорным оператором.
Спин, орбитальный и полный угловой момент

- Слева: «спиновый» момент импульса S на самом деле является орбитальным моментом импульса объекта в каждой точке.
- Справа: внешний орбитальный угловой момент L вокруг оси.
- Вверху: тензор момента инерции I и угловая скорость ω ( L не всегда параллельна ω ). [36]
- Внизу: импульс p и его радиальное положение r от оси. Полный угловой момент (спин плюс орбитальный) равен J. Для квантовой частицы интерпретации иные; спин частицы не имеет вышеуказанной интерпретации.
Классическое определение углового момента as можно перенести в квантовую механику, переосмыслив r как квантовый оператор положения , а p как квантовый оператор импульса . Тогда L является оператором , конкретно называемым оператором орбитального углового момента . Компоненты оператора углового момента удовлетворяют коммутационным соотношениям алгебры Ли so(3). Действительно, эти операторы являются в точности бесконечно малым действием группы вращений на квантовом гильбертовом пространстве . [37] (См. также обсуждение ниже операторов углового момента как генераторов вращений.)
Однако в квантовой физике существует другой тип углового момента, называемый спиновым угловым моментом , представленный оператором спина S . Спин часто изображается как частица, буквально вращающаяся вокруг оси, но это вводящая в заблуждение и неточная картина: спин является внутренним свойством частицы, не связанным с каким-либо видом движения в пространстве и принципиально отличным от орбитального углового момента. Все элементарные частицы имеют характерный спин (возможно, нулевой), [38] и почти все элементарные частицы имеют ненулевой спин. [39] Например, электроны имеют «спин 1/2» (это на самом деле означает «спин ħ /2»), фотоны имеют «спин 1» (это на самом деле означает «спин ħ»), а пи-мезоны имеют спин 0. [40]
Наконец, есть полный угловой момент J , который объединяет как спиновый, так и орбитальный угловой момент всех частиц и полей. (Для одной частицы J = L + S. ) Сохранение углового момента применимо к J , но не к L или S ; например, взаимодействие спин-орбита позволяет угловому моменту передаваться туда и обратно между L и S , при этом общий момент остается постоянным. Электроны и фотоны не обязательно должны иметь целочисленные значения для полного углового момента, но также могут иметь полуцелые значения. [41]
В молекулах полный угловой момент F является суммой ровибронного (орбитального) углового момента N , электронного спинового углового момента S и ядерного спинового углового момента I. Для электронных синглетных состояний ровибронный угловой момент обозначается как J, а не как N. Как объяснил Ван Флек [42] , компоненты молекулярного ровибронного углового момента, относящиеся к фиксированным осям молекулы, имеют иные коммутационные соотношения, чем для компонентов вокруг фиксированных в пространстве осей.
Квантование
В квантовой механике момент импульса квантуется – то есть он не может изменяться непрерывно, а только « квантовыми скачками » между определенными допустимыми значениями. Для любой системы применяются следующие ограничения на результаты измерений, где – приведенная постоянная Планка , а – любой евклидов вектор, такой как x, y или z:
| Если измерить ... | Результат может быть... |
| или | |
| , где | |
| или | , где |

Приведенная постоянная Планка мала по обыденным меркам, около 10−34 Дж с , и поэтому это квантование не оказывает заметного влияния на угловой момент макроскопических объектов. Однако оно очень важно в микроскопическом мире. Например, структура электронных оболочек и подоболочек в химии существенно зависит от квантования углового момента.
Квантование момента импульса было впервые постулировано Нильсом Бором в его модели атома и позднее предсказано Эрвином Шредингером в его уравнении Шредингера .
Неопределенность
В определении задействованы шесть операторов: операторы положения , , , и операторы импульса , , . Однако принцип неопределенности Гейзенберга говорит нам, что невозможно, чтобы все шесть этих величин были известны одновременно с произвольной точностью. Поэтому существуют пределы того, что можно узнать или измерить об угловом моменте частицы. Оказывается, лучшее, что можно сделать, — это одновременно измерить как величину вектора углового момента , так и его компоненту вдоль одной оси.
Неопределенность тесно связана с тем фактом, что различные компоненты оператора углового момента не коммутируют , например . (Для получения точных коммутационных соотношений см. оператор углового момента .)
Полный угловой момент как генератор вращений
Как упоминалось выше, орбитальный угловой момент L определяется как в классической механике: , но полный угловой момент J определяется другим, более базовым способом: J определяется как «генератор вращений». [43] Более конкретно, J определяется так, что оператор является оператором вращения , который берет любую систему и вращает ее на угол вокруг оси . («exp» в формуле относится к оператору экспоненты .) Чтобы выразить это наоборот, каким бы ни было наше квантовое гильбертово пространство, мы ожидаем, что группа вращений SO(3) будет действовать на него. Тогда существует связанное действие алгебры Ли so(3) для SO(3); операторы, описывающие действие so(3) на нашем гильбертовом пространстве, являются (полными) операторами углового момента.
Связь между оператором момента импульса и операторами вращения такая же, как связь между алгебрами Ли и группами Ли в математике. Тесная связь между моментом импульса и вращениями отражена в теореме Нётер , которая доказывает, что момент импульса сохраняется всякий раз, когда законы физики инвариантны относительно вращения.
Угловой момент в электродинамике
При описании движения заряженной частицы в электромагнитном поле канонический импульс P (выведенный из лагранжиана для этой системы) не является калибровочно-инвариантным . Как следствие, канонический угловой момент L = r × P также не является калибровочно-инвариантным. Вместо этого физический импульс, так называемый кинетический импульс (используемый в этой статье), равен (в единицах СИ )
где e — электрический заряд частицы, а A — магнитный векторный потенциал электромагнитного поля. Калибровочно-инвариантный угловой момент, то есть кинетический угловой момент , определяется как
Взаимодействие с квантовой механикой более подробно обсуждается в статье о канонических коммутационных соотношениях .
Угловой момент в оптике
В классической электродинамике Максвелла вектор Пойнтинга представляет собой линейную плотность импульса электромагнитного поля. [44]
Вектор плотности момента импульса задается векторным произведением, как в классической механике: [45]
Вышеуказанные тождества справедливы локально , т.е. в каждой точке пространства в данный момент .
Угловой момент в природе и космосе
Тропические циклоны и другие связанные с ними погодные явления включают сохранение углового момента для объяснения динамики. Ветры медленно вращаются вокруг систем низкого давления, в основном из-за эффекта Кориолиса . Если низкое давление усиливается и медленно циркулирующий воздух тянется к центру, молекулы должны ускориться, чтобы сохранить угловой момент. К тому времени, как они достигают центра, скорости становятся разрушительными. [2]
Иоганн Кеплер определил законы движения планет, не зная сохранения импульса. Однако вскоре после его открытия их вывод был определен из сохранения момента импульса. Планеты движутся тем медленнее, чем дальше они находятся на своих эллиптических орбитах, что интуитивно объясняется тем фактом, что орбитальный момент импульса пропорционален радиусу орбиты. Поскольку масса не меняется, а момент импульса сохраняется, скорость падает.
Приливное ускорение — это эффект приливных сил между естественным спутником (например, Луной ) и первичной планетой, вокруг которой он вращается (например, Землей). Гравитационный момент между Луной и приливным выступом Земли заставляет Луну постоянно продвигаться на немного более высокую орбиту (~3,8 см в год), а Землю замедлять ( на −25,858 ± 0,003″/cy²) в ее вращении ( длина дня увеличивается на ~1,7 мс за столетие, +2,3 мс из-за приливного эффекта и −0,6 мс из-за постледникового отскока). Земля теряет угловой момент, который передается Луне таким образом, что общий угловой момент сохраняется.
Угловой момент в технике и технологиях
Примеров использования сохранения углового момента для практической выгоды предостаточно. В двигателях, таких как паровые двигатели или двигатели внутреннего сгорания , маховик необходим для эффективного преобразования бокового движения поршней во вращательное движение.
Инерциальные навигационные системы явно используют тот факт, что угловой момент сохраняется относительно инерциальной системы отсчета пространства. Инерциальная навигация — это то, что позволяет подводным лодкам совершать путешествия под полярной ледяной шапкой, но также имеет решающее значение для всех форм современной навигации.
Нарезные пули используют стабильность, обеспечиваемую сохранением углового момента, чтобы быть более точными в своей траектории. Изобретение нарезного огнестрельного оружия и пушек дало их пользователям значительное стратегическое преимущество в бою и, таким образом, стало технологическим поворотным моментом в истории.
История
Исаак Ньютон в «Началах» намекнул на момент импульса в своих примерах первого закона движения :
Волчок, части которого своим сцеплением постоянно отвлекаются от прямолинейных движений, не прекращает своего вращения, иначе как задерживаясь воздухом. Более крупные тела планет и комет, встречая меньшее сопротивление в более свободных пространствах, сохраняют свои движения как поступательные, так и круговые в течение гораздо более длительного времени. [46]
Он не стал далее исследовать угловой момент непосредственно в « Началах» , заявив:
Из такого рода отражений иногда возникают также круговые движения тел вокруг их собственных центров. Но это случаи, которые я не буду рассматривать в дальнейшем; и было бы слишком утомительно доказывать каждую частность, которая относится к этому предмету. [47]
Однако его геометрическое доказательство закона площадей является выдающимся примером гениальности Ньютона и косвенно доказывает сохранение момента импульса в случае центральной силы .
Закон площадей
Вывод Ньютона
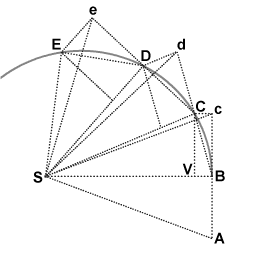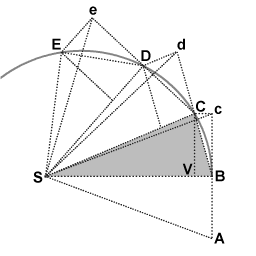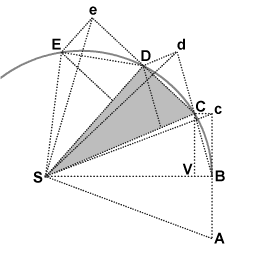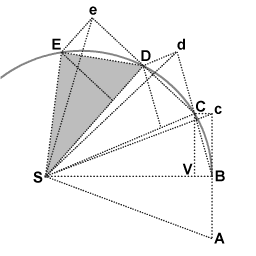
Когда планета вращается вокруг Солнца , линия между Солнцем и планетой заметает равные площади за равные промежутки времени. Это было известно с тех пор, как Кеплер изложил свой второй закон движения планет . Ньютон вывел уникальное геометрическое доказательство и продолжил показывать, что сила притяжения гравитации Солнца является причиной всех законов Кеплера.
В течение первого интервала времени объект движется из точки A в точку B. Невозмутимый, он будет продолжать движение в точку c в течение второго интервала. Когда объект прибывает в B , он получает импульс, направленный к точке S. Импульс придает ему небольшую дополнительную скорость в направлении S , так что если бы это была его единственная скорость, он двигался бы из B в V в течение второго интервала. По правилам сложения скоростей эти две скорости складываются, и точка C находится путем построения параллелограмма BcCV . Таким образом, путь объекта отклоняется импульсом так, что он достигает точки C в конце второго интервала. Поскольку треугольники SBc и SBC имеют одинаковое основание SB и одинаковую высоту Bc или VC , они имеют одинаковую площадь. По симметрии треугольник SBc также имеет такую же площадь, как треугольник SAB , поэтому объект за равные промежутки времени охватил равные площади SAB и SBC .
В точке C объект получает еще один импульс в направлении S , снова отклоняя свой путь в течение третьего интервала от d до D. Таким образом, он продолжает движение до E и далее, причем треугольники SAB , SBc , SBC , SCd , SCD , SDe , SDE имеют одинаковую площадь. Позволяя временным интервалам становиться все меньше, путь ABCDE приближается к неопределенно близкой непрерывной кривой.
Обратите внимание, что поскольку этот вывод является геометрическим и не применяется конкретная сила, он доказывает более общий закон, чем второй закон Кеплера о движении планет. Он показывает, что закон площадей применим к любой центральной силе, притягивающей или отталкивающей, непрерывной или прерывистой, или нулевой.
Сохранение момента импульса в законе площадей
Пропорциональность момента импульса площади, охватываемой движущимся объектом, можно понять, осознав, что основания треугольников, то есть линии от S до объекта, эквивалентны радиусу r, а высоты треугольников пропорциональны перпендикулярной составляющей скорости v⊥. Следовательно, если площадь, охватываемая за единицу времени, постоянна, то по формуле треугольной площади 1/2 (база)(высота) , произведение (база)(высота) и, следовательно, произведение rv ⊥ постоянны: если r и длина основания уменьшаются, v ⊥ и высота должны пропорционально увеличиваться. Масса постоянна, поэтому момент импульса rmv⊥ сохраняется при этом обмене расстоянием и скоростью.
В случае треугольника SBC площадь равна 1/2 ( SB )( VC ). Где бы в конечном итоге ни находилась точка C из-за импульса, приложенного к точке B , произведение ( SB )( VC ), а следовательно, и rmv ⊥ остаются постоянными. Аналогично для каждого из треугольников.
Другое площадное доказательство сохранения момента импульса для любой центральной силы использует теорему Мамикона о заметающих касательных. [48] [49]
После Ньютона
Леонард Эйлер , Даниил Бернулли и Патрик д'Арси все понимали угловой момент с точки зрения сохранения поверхностной скорости , что является результатом их анализа второго закона Кеплера о движении планет. Маловероятно, что они осознали последствия для обычной вращающейся материи. [50]
В 1736 году Эйлер, как и Ньютон, коснулся некоторых уравнений момента импульса в своей «Механике», не развивая их далее. [51]
В письме 1744 года Бернулли написал о «моменте вращательного движения», возможно, это была первая концепция момента импульса, как мы его сейчас понимаем. [52]
В 1799 году Пьер-Симон Лаплас впервые понял, что с вращением связана неподвижная плоскость — его неизменная плоскость .
В 1803 году Луи Пуансо начал представлять вращения в виде отрезка прямой, перпендикулярной вращению, и подробно остановился на «законе сохранения моментов».
В 1852 году Леон Фуко использовал гироскоп в эксперименте, чтобы отобразить вращение Земли.
В «Руководстве по прикладной механике» Уильяма Дж. М. Ренкина 1858 года впервые дано определение момента импульса в современном смысле:
...линия, длина которой пропорциональна величине момента импульса и направление которой перпендикулярно плоскости движения тела и неподвижной точки, и такая, что если смотреть на движение тела с конца линии, то радиус-вектор тела кажется имеющим правое вращение.
В издании той же книги 1872 года Ранкин заявил, что «термин угловой момент был введен г-ном Хейвордом» [53], вероятно, ссылаясь на статью Р. Б. Хейворда « О прямом методе оценки скоростей, ускорений и всех подобных величин относительно осей, перемещаемых любым способом в пространстве с приложениями» [54] , которая была введена в 1856 году и опубликована в 1864 году. Ранкин ошибался, поскольку многочисленные публикации содержат этот термин, начиная с конца 18-го и начала 19-го веков. [55] Однако статья Хейворда, по-видимому, была первым использованием этого термина и концепции, увиденной большей частью англоговорящего мира. До этого угловой момент обычно назывался «импульсом вращения» на английском языке. [56]
Смотрите также
- Абсолютный момент импульса
- Угловая связь импульса
- Угловой момент света
- Диаграммы углового момента (квантовая механика)
- Хаотичное вращение
- Коэффициенты Клебша–Гордана
- Линейно-вращательные аналоги
- Порядки величины (угловой момент)
- Псевдовектор Паули–Любанского
- Релятивистский момент импульса
- Жесткий ротор
- Энергия вращения
- Удельный относительный момент импульса
- Ираст
Ссылки
- ^ «Soaring Science: The Aerodynamics of Flying a Frisbee». Scientific American. 9 августа 2012 г. Получено 4 января 2022 г.
- ^ ab "Структура тропического циклона". Национальная метеорологическая служба . Получено 4 января 2022 г.
- ^ Мур, Томас (2016). Шесть идей, которые сформировали физику, раздел C: Законы сохранения ограничивают взаимодействия (третье изд.). McGraw-Hill Education. стр. 91. ISBN 978-0-07-351394-2.
- ^ ab Department of Physics and Astronomy, Georgia State University. "Moment of Inertia: Thin Disk". HyperPhysics . Получено 17 марта 2023 г.
- ^ Уилсон, Э. Б. (1915). «Линейный импульс, кинетическая энергия и угловой момент». The American Mathematical Monthly . XXII . Ginn and Co., Бостон, в сотрудничестве с Чикагским университетом и др.: 190.
- ^ Уортингтон, Артур М. (1906). Динамика вращения. Longmans, Green and Co., Лондон. стр. 21 – через Google books.
- ^ Тейлор, Джон Р. (2005). Классическая механика . University Science Books, Mill Valley, CA. стр. 90. ISBN 978-1-891389-22-1.
- ^ Дадурян, Х. М. (1913). Аналитическая механика для студентов физико-технических вузов. D. Van Nostrand Company, Нью-Йорк. стр. 266 – через Google books.
- ^ Уотсон, У. (1912). Общая физика. Longmans, Green and Co., Нью-Йорк. стр. 33 – через Google books.
- ^ Баркер, Джордж Ф. (1893). Физика: Продвинутый курс (4-е изд.). Henry Holt and Company, Нью-Йорк. стр. 66 – через Google Books.
- ^ Баркер, Джордж Ф. (1893). Физика: Продвинутый курс (4-е изд.). Henry Holt and Company, Нью-Йорк. стр. 67–68 – через Google Books.
- ^ Оберг, Эрик и др. (2000). Справочник по машиностроению (26-е изд.). Industrial Press, Inc., Нью-Йорк. стр. 143. ISBN 978-0-8311-2625-4.
- ^ Уотсон, У. (1912). Общая физика. Longmans, Green and Co., Нью-Йорк. стр. 34 – через Google books.
- ^ Кент, Уильям (1916). Карманный справочник инженеров-механиков (9-е изд.). John Wiley and Sons, Inc., Нью-Йорк. стр. 517 – через Google books.
- ^ Оберг, Эрик и др. (2000). Справочник по машиностроению (26-е изд.). Industrial Press, Inc., Нью-Йорк. стр. 146. ISBN 978-0-8311-2625-4.
- ^ Оберг, Эрик и др. (2000). Machinery's Handbook (26-е изд.). Industrial Press, Inc., Нью-Йорк. С. 161–162. ISBN 978-0-8311-2625-4.
- ^ Кент, Уильям (1916). Карманный справочник инженеров-механиков (9-е изд.). John Wiley and Sons, Inc., Нью-Йорк. стр. 527 – через Google books.
- ^ Баттин, Ричард Х. (1999). Введение в математику и методы астродинамики, пересмотренное издание . Американский институт аэронавтики и астронавтики, Inc. ISBN 978-1-56347-342-5., стр. 97
- ^ Rankine, WJM (1872). Руководство по прикладной механике (6-е изд.). Charles Griffin and Company, Лондон. стр. 507 – через Google books.
- ^ ab Crew, Henry (1908). Принципы механики: для студентов физики и инженерии. Longmans, Green, and Company, Нью-Йорк. стр. 88 – через Google books.
- ^ Уортингтон, Артур М. (1906). Динамика вращения. Longmans, Green and Co., Лондон. стр. 82 – через Google books.
- ^ Уортингтон, Артур М. (1906). Динамика вращения. Longmans, Green and Co., Лондон. стр. 11 – через Google books.
- ^ Стивенсон, FR; Моррисон, LV; Уитроу, GJ (1984). «Долгосрочные изменения во вращении Земли – 700 г. до н. э. – 1980 г. н. э.». Philosophical Transactions of the Royal Society . 313 (1524): 47–70. Bibcode : 1984RSPTA.313...47S. doi : 10.1098/rsta.1984.0082. S2CID 120566848.+2,40 мс/столетие деленное на 36525 дней.
- ^ Дики, Дж. О.; и др. (1994). «Лазерная локация Луны: продолжающееся наследие программы «Аполлон»» (PDF) . Science . 265 (5171): 482–90, см. 486. Bibcode :1994Sci...265..482D. doi :10.1126/science.265.5171.482. PMID 17781305. S2CID 10157934. Архивировано (PDF) из оригинала 2022-10-09.
- ^ Ландау, Л. Д.; Лифшиц, Э. М. (1995). Классическая теория полей . Курс теоретической физики. Оксфорд, Баттерворт–Хайнеманн. ISBN 978-0-7506-2768-9.
- ^ Тененбаум, М. и Поллард, Х. (1985). Обыкновенные дифференциальные уравнения в элементарном учебнике для студентов-математиков. Инженерное дело и науки.
- ^ Рамон, Пьер (2020). Теория поля: современный учебник (2-е изд.). Routledge. ISBN 9780429689017.Выдержка из страницы 1
- ^ Дэвид Морин (2008). Введение в классическую механику: с проблемами и решениями. Cambridge University Press. стр. 311. ISBN 978-1-139-46837-4.Выдержка из страницы 311
- ^ Баттин, Ричард Х. (1999). Введение в математику и методы астродинамики, пересмотренное издание . Американский институт аэронавтики и астронавтики, Inc. стр. 115. ISBN 978-1-56347-342-5.
- ^ Уилсон, Э. Б. (1915). «Линейный импульс, кинетическая энергия и угловой момент». The American Mathematical Monthly . XXII . Ginn and Co., Бостон, в сотрудничестве с Чикагским университетом и др.: 188, уравнение (3).
- ^ Уилсон, Э. Б. (1915). «Линейный импульс, кинетическая энергия и угловой момент». The American Mathematical Monthly . XXII . Ginn and Co., Бостон, в сотрудничестве с Чикагским университетом и др.: 191, Теорема 8.
- ^ Хокинг, SW; Эллис, GFR (1973). Крупномасштабная структура пространства-времени. Cambridge University Press. стр. 62–63. doi :10.1017/CBO9780511524646. ISBN 978-0-521-09906-6.
- ^ Мизнер, CW; Торн, KS; Уилер, JA (1973). "20: Законы сохранения для 4-импульса и углового момента". Гравитация. WH Freeman and Company.
- ^ Синг и Шильд, Тензорное исчисление, Dover Publications, издание 1978 г., стр. 161. ISBN 978-0-486-63612-2 .
- ^ де Подеста, Майкл (2002). Понимание свойств материи (2-е, иллюстрированное, исправленное издание). CRC Press. стр. 29. ISBN 978-0-415-25788-6.
- ^ RP Feynman; RB Leighton; M. Sands (1964). Лекции Фейнмана по физике (том 2) . Addison–Wesley. стр. 31–7. ISBN 978-0-201-02117-2.
- ^ Холл 2013 Раздел 17.3
- ^ Велтман, Мартинус Дж. Г. (2018). Факты и тайны в физике элементарных частиц (пересмотренное издание). World Scientific. ISBN 978-981-323-707-0.
- ^ Thaller, Bernd (2005). Advanced Visual Quantum Mechanics (иллюстрированное издание). Springer Science & Business Media. стр. 114. ISBN 978-0-387-27127-9.
- ^ Strange, Paul (1998). Relativistic Quantum Mechanics: With Applications in Condensed Matter and Atomic Physics (иллюстрированное издание). Cambridge University Press. стр. 64. ISBN 978-0-521-56583-7.
- ^ Ballantine, KE; Donegan, JF; Eastham, PR (2016). «Существует много способов вращать фотон: полуквантование полного оптического углового момента». Science Advances . 2 (4): e1501748. Bibcode : 2016SciA....2E1748B. doi : 10.1126/sciadv.1501748. PMC 5565928. PMID 28861467 .
- ^ JH Van Vleck (1951). "Связь векторов углового момента в молекулах". Rev. Mod. Phys . 23 (3): 213. Bibcode :1951RvMP...23..213V. doi :10.1103/RevModPhys.23.213.
- ^ Littlejohn, Robert (2011). "Lecture notes on rotations in quantum mechanics" (PDF) . Physics 221B Spring 2011 . Архивировано (PDF) из оригинала 2022-10-09 . Получено 13 января 2012 .
- ^ Окулов, А Ю (2008). "Угловой момент фотонов и фазовое сопряжение". Журнал физики B: атомная, молекулярная и оптическая физика . 41 (10): 101001. arXiv : 0801.2675 . Bibcode :2008JPhB...41j1001O. doi :10.1088/0953-4075/41/10/101001. S2CID 13307937.
- ^ Окулов, А.Ю. (2008). «Оптические и звуковые спиральные структуры в зеркале Мандельштама – Бриллюэна». Письма в ЖЭТФ . 88 (8): 561–566. Bibcode :2008JETPL..88..487O. doi :10.1134/s0021364008200046. S2CID 120371573. Архивировано из оригинала 22.12.2015 . Получено 31.10.2015 .
- ^ Ньютон, Исаак (1803). «Аксиомы; или Законы движения, Закон I». Математические начала натуральной философии . Эндрю Мотт, переводчик. HD Symonds, Лондон. стр. 322 – через Google books.
- ^ Ньютон, Аксиомы, или Законы движения, Следствие III
- ^ Withers, LP (2013). «Визуальный угловой момент: Мамикон встречает Кеплера». American Mathematical Monthly . 120 (1): 71–73. doi :10.4169/amer.math.monthly.120.01.071. S2CID 30994835.
- ^ Апостол, Том М.; Мнацаканян, Мамикон А. (2012). Новые горизонты в геометрии . МАА Пресс. стр. 29–30. ISBN 978-1-4704-4335-1.
- ^ см. Боррелли, Арианна (2011). "Угловой момент между физикой и математикой" (PDF) . Архивировано (PDF) из оригинала 2022-10-09.за превосходное и подробное изложение концепции момента импульса в истории.
- ^ Брюс, Ян (2008). «Эйлер: Механика, том 1».
- ^ "Переписка Эйлера с Даниилом Бернулли, Бернулли Эйлеру, 4 февраля 1744 г." (PDF) . Архив Эйлера . Архивировано (PDF) из оригинала 2022-10-09.
- ^ Rankine, WJM (1872). Руководство по прикладной механике (6-е изд.). Charles Griffin and Company, Лондон. стр. 506 – через Google books.
- ^ Хейворд, Роберт Б. (1864). «О прямом методе оценки скоростей, ускорений и всех подобных величин относительно осей, перемещаемых любым способом в пространстве, с приложениями». Труды Кембриджского философского общества . 10 : 1. Бибкод : 1864TCaPS..10....1H.
- ^ см., например, Гомпертц, Бенджамин (1818). «О маятниках, вибрирующих между щеками». Журнал науки и искусств . III (V): 17 – через Google books.; Херапат, Джон (1847). Математическая физика. Whittaker and Co., Лондон. стр. 56 – через Google books.
- ^ см., например, Ланден, Джон (1785). «О вращательном движении тела любой формы». Philosophical Transactions . LXXV (I): 311–332. doi :10.1098/rstl.1785.0016. S2CID 186212814.
Дальнейшее чтение
- Коэн-Таннуджи, Клод; Диу, Бернар; Лалоэ, Франк (2006). Квантовая механика (2-томное изд.). Джон Уайли и сыновья. ISBN 978-0-471-56952-7.
- Condon, EU; Shortley, GH (1935). "Глава III: Угловой момент". Теория атомных спектров . Cambridge University Press. ISBN 978-0-521-09209-8.
- Эдмондс, AR (1957). Угловой момент в квантовой механике . Princeton University Press. ISBN 978-0-691-07912-7.
- Холл, Брайан С. (2013), Квантовая теория для математиков , Graduate Texts in Mathematics, т. 267, Springer, Bibcode : 2013qtm..book.....H, ISBN 978-0-387-40122-5.
- Джексон, Джон Дэвид (1998). Классическая электродинамика (3-е изд.). John Wiley & Sons. ISBN 978-0-471-30932-1.
- Serway, Raymond A.; Jewett, John W. (2004). Физика для ученых и инженеров (6-е изд.). Brooks/Cole. ISBN 978-0-534-40842-8.
- Томпсон, Уильям Дж. (1994). Угловой момент: иллюстрированное руководство по вращательным симметриям для физических систем . Wiley. ISBN 978-0-471-55264-2.
- Типлер, Пол (2004). Физика для ученых и инженеров: механика, колебания и волны, термодинамика (5-е изд.). WH Freeman. ISBN 978-0-7167-0809-4.
- Фейнман Р.; Лейтон Р .; Сэндс М. (сентябрь 2013 г.). «19–4 Вращательная кинетическая энергия». Лекции Фейнмана по физике (онлайн-ред.) – через веб-сайт лекций Фейнмана.
Внешние ссылки
- «Что общего у подводной лодки, ракеты и футбольного мяча? Почему вытянутый сфероид — это форма успеха» ( Scientific American , 8 ноября 2010 г.)
- Сохранение углового момента Архивировано 2016-12-07 в Wayback Machine – глава из онлайн-учебника
- Угловой момент в процессе столкновения – вывод трехмерного случая
- Угловой момент и качение – больше о теории импульса










































































![{\displaystyle S\left([x_{i}];t_{1},t_{2}\right)\equiv \int _{t_{1}}^{t_{2}}dt\left({\frac {1}{2}}m{\frac {dx_{i}}{dt}}\ {\frac {dx_{i}}{dt}}-V(x_{i})\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a1a0a77886ae741be2679b9b7123e90de2e3ae9)
![{\textstyle \delta S=S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right)-S\left([x_{i}];t_{1},t_{2}\right)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/560e494d7450ac05174984f59efb1377447616e5)

![{\displaystyle S\left([x_{i}+\delta x_{i}];t_{1},t_{2}\right)=\!\int _{t_{1}}^{t_{2}}dt\left({\frac {1}{2}}m{\frac {d(x_{i}+\delta x_{i})}{dt}}{\frac {d(x_{i}+\delta x_{i})}{dt}}-V(x_{i}+\delta x_{i})\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6cea9bc1b2c5c3fe5c29911ab7cedd3b088354b)


![{\displaystyle S[x_{i}+\delta x_{i}]\simeq S[x_{i}]+\int _{t_{1}}^{t_{2}}dt\,\delta x_{i}\left(-{\frac {\partial V}{\partial x_{i}}}-m{\frac {d^{2}x_{i}}{dt^{2}}}\right)+m\int _{t_{1}}^{t_{2}}dt{\frac {d}{dt}}\left(\delta x_{i}{\frac {dx_{i}}{dt}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3d0a75604f66354be4b20123019ee46516b215e)














































![{\displaystyle {\begin{align}\mathbf {L} &=\sum _{i}\left[\left(\mathbf {R} +\mathbf {r} _{i}\right)\times m_{i}\mathbf {V} _{i}\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} _{i}\right]\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77077ef30b49ac992b78c6a4c6446709bb1720a9)
![{\displaystyle {\begin{aligned}\mathbf {L} &=\sum _{i}\left[\mathbf {R} \times m_{i}\left(\mathbf {V} +\mathbf {v} _{i}\right)+\mathbf {r} _{i}\times m_{i}(\mathbf {V} +\mathbf {v} _{i})\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} +\mathbf {R} \times m_{i}\mathbf {v} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} +\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\right]\\&=\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} +\sum _{i}\mathbf {R} \times m_{i}\mathbf {v} _{i}+\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4784bd78e4066783f47bd72472bfa49a0887b0bf)








![{\displaystyle {\begin{aligned}\mathbf {L} &=M(\mathbf {R} \times \mathbf {V} )+\sum _{i}\left[m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&={\frac {R^{2}}{R^{2}}}M\left(\mathbf {R} \times \mathbf {V} \right)+\sum _{i}\left[{\frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&=R^{2}M\left({\frac {\mathbf {R} \times \mathbf {V} }{R^{2}}}\right)+\sum _{i}\left[r_{i}^{2}m_{i}\left({\frac {\mathbf {r} _{i}\times \mathbf {v} _{i}}{r_{i}^{2}}}\right)\right],\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5324c7fa7e5e94893f678fab046c2538416bc51)































![{\displaystyle \left[\hbar ^{2}n(n+1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd720bdca13e8588818fb477347fb90c9789bb4a)























