Атом водорода
 | |
| Общий | |
|---|---|
| Символ | 1 ч. |
| Имена | атом водорода, 1H, H-1, протий |
| Протоны ( Z ) | 1 |
| Нейтроны ( N ) | 0 |
| Данные по нуклидам | |
| Естественное изобилие | 99,985% |
| Период полураспада ( t 1/2 ) | стабильный |
| Масса изотопа | 1,007825 Да |
| Вращаться | 1/2 |
| Избыток энергии | 7 288 .969 ± 0,001 кэВ |
| Энергия связи | 0,000 ± 0,0000 кэВ |
| Изотопы водорода Полная таблица нуклидов | |
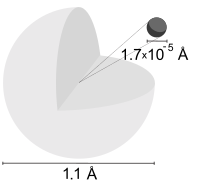
Атом водорода — атом химического элемента водорода . Электрически нейтральный атом водорода содержит ядро из одного положительно заряженного протона и одного отрицательно заряженного электрона, связанного с ядром кулоновской силой . Атомарный водород составляет около 75% барионной массы Вселенной. [1]
В повседневной жизни на Земле изолированные атомы водорода (называемые «атомарным водородом») встречаются крайне редко. Вместо этого атом водорода имеет тенденцию объединяться с другими атомами в соединениях или с другим атомом водорода, образуя обычный ( двухатомный ) водородный газ, H2 . «Атомарный водород» и «атом водорода» в обычном английском языке имеют перекрывающиеся, но различные значения. Например, молекула воды содержит два атома водорода, но не содержит атомарного водорода (что относилось бы к изолированным атомам водорода).
Атомная спектроскопия показывает, что существует дискретный бесконечный набор состояний, в которых может существовать атом водорода (или любой другой), вопреки предсказаниям классической физики . Попытки разработать теоретическое понимание состояний атома водорода были важны для истории квантовой механики , поскольку все другие атомы можно приблизительно понять, зная в деталях эту простейшую атомную структуру.
Изотопы
Самый распространенный изотоп , протий ( 1 H), или легкий водород, не содержит нейтронов и представляет собой просто протон и электрон . Протий стабилен и составляет 99,985% атомов водорода, встречающихся в природе. [2]
Дейтерий ( 2H ) содержит один нейтрон и один протон в своем ядре. Дейтерий стабилен, составляет 0,0156% природного водорода, [2] и используется в промышленных процессах, таких как ядерные реакторы и ядерный магнитный резонанс .
Тритий ( 3 H) содержит два нейтрона и один протон в своем ядре и нестабилен, распадаясь с периодом полураспада 12,32 года. Из-за своего короткого периода полураспада тритий не существует в природе, за исключением следовых количеств.
Более тяжелые изотопы водорода создаются только искусственно в ускорителях частиц и имеют период полураспада порядка 10−22 секунд . Они представляют собой несвязанные резонансы, расположенные за пределами нейтронной границы ; это приводит к быстрому испусканию нейтрона .
Приведенные ниже формулы справедливы для всех трех изотопов водорода, но для каждого изотопа водорода необходимо использовать немного отличающиеся значения постоянной Ридберга (корректирующая формула приведена ниже).
Ион водорода
Одиночные нейтральные атомы водорода редки при нормальных условиях. Однако нейтральный водород распространен, когда он ковалентно связан с другим атомом, и атомы водорода могут также существовать в катионных и анионных формах.
Если нейтральный атом водорода теряет свой электрон, он становится катионом. Полученный ион, который состоит исключительно из протона для обычного изотопа, записывается как "H + " и иногда называется гидроном . Свободные протоны обычны в межзвездной среде и солнечном ветре . В контексте водных растворов классических кислот Бренстеда-Лоури , таких как соляная кислота , на самом деле подразумевается гидроний , H 3 O + . Вместо того, чтобы буквально образовывать ионизированный одиночный атом водорода, кислота переносит водород в H 2 O, образуя H 3 O + .
Если вместо этого атом водорода получает второй электрон, он становится анионом. Анион водорода записывается как "H– " и называется гидридом .
Теоретический анализ
Атом водорода имеет особое значение в квантовой механике и квантовой теории поля как простая физическая система двух тел , которая дала множество простых аналитических решений в замкнутой форме.
Неудачное классическое описание
Эксперименты Эрнеста Резерфорда в 1909 году показали, что структура атома представляет собой плотное положительное ядро с разреженным облаком отрицательного заряда вокруг него. Это сразу же вызвало вопросы о том, как такая система может быть стабильной. Классический электромагнетизм показал, что любой ускоряющийся заряд излучает энергию, как показано в формуле Лармора . Если предположить, что электрон движется по идеальной окружности и непрерывно излучает энергию, электрон быстро по спирали войдет в ядро со временем падения: [3] где — радиус Бора , а — классический радиус электрона . Если бы это было так, все атомы мгновенно бы разрушились. Однако атомы кажутся стабильными. Более того, спираль вовнутрь высвободила бы размытость электромагнитных частот по мере уменьшения орбиты. Вместо этого было обнаружено, что атомы излучают только дискретные частоты излучения. Решением стало бы развитие квантовой механики .
Модель Бора-Зоммерфельда
В 1913 году Нильс Бор получил энергетические уровни и спектральные частоты атома водорода, сделав ряд простых предположений, чтобы исправить несостоятельную классическую модель. Предположения включали:
- Электроны могут находиться только на определенных, дискретных круговых орбитах или в стационарных состояниях , тем самым имея дискретный набор возможных радиусов и энергий.
- Электроны не испускают излучение, находясь в одном из этих стационарных состояний.
- Электрон может приобретать или терять энергию, переходя с одной дискретной орбиты на другую.
Бор предположил, что угловой момент электрона квантуется с возможными значениями: где и — постоянная Планка над . Он также предположил, что центростремительная сила , которая удерживает электрон на его орбите, обеспечивается силой Кулона , и что энергия сохраняется. Бор вывел энергию каждой орбиты атома водорода следующим образом: [4] где — масса электрона , — заряд электрона , — диэлектрическая проницаемость вакуума , — квантовое число (теперь известное как главное квантовое число ). Предсказания Бора совпали с экспериментами по измерению спектральной серии водорода до первого порядка, что придало большую уверенность теории, которая использовала квантованные значения.
Для величина [5] называется единицей энергии Ридберга. Она связана с постоянной Ридберга атомной физики соотношением
Точное значение постоянной Ридберга предполагает, что ядро бесконечно массивно по отношению к электрону. Для водорода-1, водорода-2 ( дейтерия ) и водорода-3 ( трития ), которые имеют конечную массу, константу необходимо немного изменить, чтобы использовать приведенную массу системы, а не просто массу электрона. Это включает кинетическую энергию ядра в задаче, поскольку полная (электронная плюс ядерная) кинетическая энергия эквивалентна кинетической энергии приведенной массы, движущейся со скоростью, равной скорости электрона относительно ядра. Однако, поскольку ядро намного тяжелее электрона, масса электрона и приведенная масса почти одинаковы. Постоянная Ридберга R M для атома водорода (один электрон), R определяется как, где - масса атомного ядра. Для водорода-1 эта величина составляет около 1/1836 (т. е. отношение масс электрона к протону). Для дейтерия и трития эти отношения составляют около 1/3670 и 1/5497 соответственно. Эти цифры, если их добавить к 1 в знаменателе, представляют собой очень небольшие поправки к значению R и, следовательно, лишь небольшие поправки ко всем уровням энергии в соответствующих изотопах водорода.
В модели Бора все еще оставались проблемы:
- он не смог предсказать другие спектральные детали, такие как тонкая структура и сверхтонкая структура
- он мог предсказать уровни энергии с какой-либо точностью только для одноэлектронных атомов (атомов, подобных водороду)
- предсказанные значения были верны только для , где - постоянная тонкой структуры .
Большинство этих недостатков были устранены модификацией модели Бора Арнольдом Зоммерфельдом . Зоммерфельд ввел две дополнительные степени свободы, что позволило электрону двигаться по эллиптической орбите, характеризующейся его эксцентриситетом и наклонением относительно выбранной оси. Это ввело два дополнительных квантовых числа, которые соответствуют орбитальному угловому моменту и его проекции на выбранную ось. Таким образом, была найдена правильная множественность состояний (за исключением фактора 2, учитывающего пока неизвестный спин электрона). Далее, применив специальную теорию относительности к эллиптическим орбитам, Зоммерфельду удалось вывести правильное выражение для тонкой структуры спектров водорода (которое оказалось точно таким же, как в самой сложной теории Дирака). Однако некоторые наблюдаемые явления, такие как аномальный эффект Зеемана , остались необъясненными. Эти вопросы были решены с полным развитием квантовой механики и уравнения Дирака . Часто утверждается, что уравнение Шредингера превосходит теорию Бора–Зоммерфельда в описании атома водорода. Это не так, поскольку большинство результатов обоих подходов совпадают или очень близки (замечательным исключением является задача об атоме водорода в скрещенных электрическом и магнитном полях, которая не может быть самосогласованно решена в рамках теории Бора–Зоммерфельда), а в обеих теориях основные недостатки вытекают из отсутствия спина электрона. Полная неспособность теории Бора–Зоммерфельда объяснить многоэлектронные системы (такие как атом гелия или молекула водорода) продемонстрировала ее неадекватность для описания квантовых явлений.
Уравнение Шредингера
Уравнение Шредингера — это стандартная модель квантовой механики; оно позволяет вычислять стационарные состояния, а также временную эволюцию квантовых систем. Точные аналитические ответы доступны для нерелятивистского атома водорода. Прежде чем перейти к представлению формального отчета, здесь мы дадим элементарный обзор.
Учитывая, что атом водорода содержит ядро и электрон, квантовая механика позволяет предсказать вероятность нахождения электрона на любом заданном радиальном расстоянии . Она задается квадратом математической функции, известной как « волновая функция », которая является решением уравнения Шредингера. Состояние равновесия атома водорода с наименьшей энергией известно как основное состояние. Волновая функция основного состояния известна как волновая функция. Она записывается как:
Здесь — численное значение радиуса Бора. Плотность вероятности нахождения электрона на расстоянии в любом радиальном направлении — это квадрат значения волновой функции:
Волновая функция сферически симметрична, а площадь поверхности оболочки на расстоянии равна , поэтому полная вероятность нахождения электрона в оболочке на расстоянии и толщине равна
Оказывается, это максимум при . То есть, картина Бора электрона, вращающегося вокруг ядра в радиусе, соответствует наиболее вероятному радиусу. На самом деле, существует конечная вероятность того, что электрон может быть найден в любом месте , с вероятностью, указанной квадратом волновой функции. Поскольку вероятность нахождения электрона где-то во всем объеме равна единице, интеграл от равен единице. Тогда мы говорим, что волновая функция правильно нормирована.
Как обсуждается ниже, основное состояние также обозначается квантовыми числами . Вторые по низшей энергии состояния, сразу над основным состоянием, задаются квантовыми числами , , и . Все эти состояния имеют одинаковую энергию и известны как состояния и . Существует одно состояние: и существует три состояния:
Электрон в состоянии или с наибольшей вероятностью будет находиться на второй орбите Бора с энергией, определяемой формулой Бора.
Волновая функция
Гамильтониан атома водорода — это оператор радиальной кинетической энергии плюс кулоновская электростатическая потенциальная энергия между положительным протоном и отрицательным электроном. Используя не зависящее от времени уравнение Шредингера, игнорируя все спин-связывающие взаимодействия и используя приведенную массу , уравнение записывается как:
Разложение Лапласа в сферических координатах:
Это разделяемое , частное дифференциальное уравнение , которое может быть решено в терминах специальных функций. Когда волновая функция разделяется как произведение функций , , и появляются три независимые дифференциальные функции [6] с A и B, являющимися константами разделения:
- радиальный:
- полярный:
- азимут:
Нормализованные волновые функции положения , заданные в сферических координатах, имеют вид:
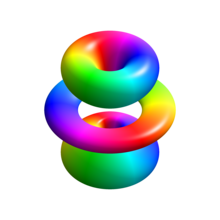
где:
- ,
- - приведенный радиус Бора , ,
- является обобщенным полиномом Лагерра степени , и
- является сферической гармонической функцией степени и порядка .
Обратите внимание, что обобщенные полиномы Лагерра определяются разными авторами по-разному. Использование здесь согласуется с определениями, используемыми Messiah, [7] и Mathematica. [8] В других местах полином Лагерра включает множитель , [9] или обобщенный полином Лагерра, появляющийся в волновой функции водорода , вместо этого. [10]
Квантовые числа могут принимать следующие значения:
Кроме того, эти волновые функции нормализованы (т.е. интеграл квадрата их модуля равен 1) и ортогональны : где — состояние, представленное волновой функцией в нотации Дирака , а — дельта-функция Кронекера . [11]
Волновые функции в импульсном пространстве связаны с волновыми функциями в пространстве положений посредством преобразования Фурье , которое для связанных состояний приводит к [12] где обозначает полином Гегенбауэра и находится в единицах .
Решения уравнения Шредингера для водорода являются аналитическими , давая простое выражение для энергетических уровней водорода и, следовательно, частот спектральных линий водорода , и полностью воспроизводя модель Бора и выходя за ее рамки. Оно также дает два других квантовых числа и форму волновой функции электрона («орбиталь») для различных возможных квантово-механических состояний, тем самым объясняя анизотропный характер атомных связей.
Уравнение Шредингера применимо также к более сложным атомам и молекулам . Когда имеется более одного электрона или ядра, решение не является аналитическим и необходимы либо компьютерные вычисления, либо должны быть сделаны упрощающие предположения.
Поскольку уравнение Шредингера справедливо только для нерелятивистской квантовой механики, решения, которые оно дает для атома водорода, не совсем верны. Уравнение Дирака релятивистской квантовой теории улучшает эти решения (см. ниже).
Результаты уравнения Шредингера
Решение уравнения Шредингера (волнового уравнения) для атома водорода использует тот факт, что кулоновский потенциал, создаваемый ядром, является изотропным (он радиально симметричен в пространстве и зависит только от расстояния до ядра). Хотя результирующие собственные функции энергии ( орбитали ) не обязательно сами изотропны, их зависимость от угловых координат в общем случае полностью следует из этой изотропии базового потенциала: собственные состояния гамильтониана (то есть собственные состояния энергии) могут быть выбраны как одновременные собственные состояния оператора углового момента . Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Следовательно, собственные состояния энергии могут быть классифицированы двумя квантовыми числами углового момента , и (оба являются целыми числами). Квантовое число углового момента определяет величину углового момента. Магнитное квантовое число определяет проекцию углового момента на (произвольно выбранную) ось .
В дополнение к математическим выражениям для полного углового момента и проекции углового момента волновых функций, необходимо найти выражение для радиальной зависимости волновых функций. Только здесь вступают в действие детали кулоновского потенциала (приводящие к полиномам Лагерра в ). Это приводит к третьему квантовому числу, главному квантовому числу . Главное квантовое число в водороде связано с полной энергией атома.
Обратите внимание, что максимальное значение квантового числа момента импульса ограничено главным квантовым числом: оно может достигать только , т. е . .
Из-за сохранения углового момента состояния одинаковых, но разных имеют одинаковую энергию (это справедливо для всех задач с вращательной симметрией ). Кроме того, для атома водорода состояния одинаковых , но разных также вырождены (т. е. имеют одинаковую энергию). Однако это специфическое свойство водорода и больше не относится к более сложным атомам, которые имеют (эффективный) потенциал, отличающийся от формы (из-за наличия внутренних электронов, экранирующих потенциал ядра).
Учет спина электрона добавляет последнее квантовое число, проекцию спинового момента импульса электрона вдоль оси , которая может принимать два значения. Таким образом, любое собственное состояние электрона в атоме водорода полностью описывается четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это также объясняет, почему выбор оси для направленного квантования вектора момента импульса несущественен: орбиталь заданной и полученной для другой предпочтительной оси всегда можно представить как подходящую суперпозицию различных состояний разных (но одинаковых ), которые были получены для .
Математическое резюме собственных состояний атома водорода
В 1928 году Поль Дирак нашел уравнение , которое было полностью совместимо со специальной теорией относительности , и (как следствие) сделал волновую функцию 4-компонентным « спинором Дирака », включающим компоненты спина «вверх» и «вниз», как с положительной, так и с «отрицательной» энергией (или материей и антиматерией). Решение этого уравнения дало следующие результаты, более точные, чем решение Шредингера.
Уровни энергии
Уровни энергии водорода, включая тонкую структуру (исключая сдвиг Лэмба и сверхтонкую структуру ), задаются выражением тонкой структуры Зоммерфельда : [13] где — постоянная тонкой структуры , а — квантовое число полного углового момента , которое равно , в зависимости от ориентации спина электрона относительно орбитального углового момента. [14] Эта формула представляет собой небольшую поправку к энергии, полученной Бором и Шредингером, как указано выше. Множитель в квадратных скобках в последнем выражении близок к единице; дополнительный член возникает из-за релятивистских эффектов (подробнее см. в разделе #Особенности, выходящие за рамки решения Шредингера). Стоит отметить, что это выражение было впервые получено А. Зоммерфельдом в 1916 году на основе релятивистской версии старой теории Бора . Однако Зоммерфельд использовал другие обозначения для квантовых чисел.
Визуализация электронных орбиталей водорода

На изображении справа показаны первые несколько орбиталей атома водорода (собственные функции энергии). Это поперечные сечения плотности вероятности , которые имеют цветовую кодировку (черный цвет представляет нулевую плотность, а белый цвет представляет самую высокую плотность). Квантовое число углового момента (орбитальное) ℓ обозначено в каждом столбце с использованием обычного спектроскопического буквенного кода ( s означает ℓ = 0, p означает ℓ = 1, d означает ℓ = 2). Главное (главное) квантовое число n (= 1, 2, 3, ...) отмечено справа от каждой строки. Для всех изображений магнитное квантовое число m установлено равным 0, а плоскость поперечного сечения является плоскостью xz ( z — вертикальная ось). Плотность вероятности в трехмерном пространстве получается путем вращения показанной здесь вокруг оси z .
« Основное состояние », т.е. состояние с наименьшей энергией, в котором обычно находится электрон, — это первое состояние, состояние 1s ( главный квантовый уровень n = 1, ℓ = 0).
Черные линии встречаются на каждой орбитали, кроме первой: это узлы волновой функции, то есть места, где плотность вероятности равна нулю. (Точнее, узлы — это сферические гармоники , которые появляются в результате решения уравнения Шредингера в сферических координатах.)
Квантовые числа определяют расположение этих узлов. Существуют: [ необходима цитата ]
- общее количество узлов,
- из которых угловые узлы:
- Угловые узлы располагаются вокруг оси (в плоскости xy ). (На рисунке выше эти узлы не показаны, поскольку на нем изображены поперечные сечения через плоскость xz .)
- (остальные угловые узлы) находятся на (вертикальной) оси.
- (остальные неугловые узлы) являются радиальными узлами.
Колебание орбиталей

Частота состояния на уровне n равна , поэтому в случае суперпозиции нескольких орбиталей они будут колебаться из-за разницы в частоте. Например, два состояния, ψ 1 и ψ 2 : Волновая функция задается как , а функция вероятности равна

Результатом является вращающаяся волновая функция. Движение электронов и изменение квантовых состояний излучает свет с частотой косинуса.
Возможности, выходящие за рамки решения Шредингера
Существует несколько важных эффектов, которые не учитываются уравнением Шредингера и которые ответственны за некоторые небольшие, но измеримые отклонения реальных спектральных линий от предсказанных:
- Хотя средняя скорость электрона в водороде составляет всего 1/137 скорости света , многие современные эксперименты достаточно точны, чтобы полное теоретическое объяснение требовало полностью релятивистского подхода к проблеме. Релятивистский подход приводит к увеличению импульса электрона примерно на 1 часть из 37 000. Поскольку длина волны электрона определяется его импульсом, орбитали, содержащие электроны с большей скоростью, демонстрируют сокращение из-за меньших длин волн.
- Даже когда нет внешнего магнитного поля , в инерциальной системе отсчета движущегося электрона электромагнитное поле ядра имеет магнитную составляющую. Спин электрона имеет связанный магнитный момент , который взаимодействует с этим магнитным полем. Этот эффект также объясняется специальной теорией относительности, и он приводит к так называемой спин-орбитальной связи , т. е. взаимодействию между орбитальным движением электрона вокруг ядра и его спином .
Обе эти особенности (и даже больше) включены в релятивистское уравнение Дирака , с предсказаниями, которые еще ближе к эксперименту. Опять же, уравнение Дирака может быть решено аналитически в частном случае двухчастичной системы, такой как атом водорода. Полученные квантовые состояния решения теперь должны быть классифицированы по полному угловому моменту j (возникающему из-за связи между спином электрона и орбитальным угловым моментом ). Состояния с тем же j и тем же n по-прежнему вырождены. Таким образом, прямое аналитическое решение уравнения Дирака предсказывает 2S( 1/2 ) и 2P( 1/2 ) уровни водорода имеют абсолютно одинаковую энергию, что противоречит наблюдениям ( эксперимент Лэмба–Резерфорда ).
- Согласно квантовой механике, всегда существуют вакуумные флуктуации электромагнитного поля . Из-за таких флуктуаций вырождение между состояниями с одинаковым j, но разными l снимается, что дает им немного разные энергии. Это было продемонстрировано в знаменитом эксперименте Лэмба-Резерфорда и стало отправной точкой для развития теории квантовой электродинамики (которая способна иметь дело с этими вакуумными флуктуациями и использует знаменитые диаграммы Фейнмана для приближений с использованием теории возмущений ). Этот эффект теперь называется сдвигом Лэмба .
Для этих разработок было важно, чтобы решение уравнения Дирака для атома водорода могло быть получено точно, так что любое экспериментально наблюдаемое отклонение следовало воспринимать серьезно как сигнал о несостоятельности теории.
Альтернативы теории Шредингера
На языке матричной механики Гейзенберга атом водорода был впервые решен Вольфгангом Паули [15] с использованием вращательной симметрии в четырех измерениях [O(4)-симметрия], порожденной угловым моментом и вектором Лапласа-Рунге-Ленца . Расширяя группу симметрии O(4) до динамической группы O(4,2), весь спектр и все переходы были вложены в единое неприводимое групповое представление. [16]
В 1979 году Дуру и Кляйнерт впервые решили задачу (нерелятивистского) атома водорода в рамках интеграла по траекториям Фейнмана в квантовой механике . [17] [18] Эта работа значительно расширила область применимости метода Фейнмана .
Другими альтернативными моделями являются механика Бома и сложная формулировка Гамильтона-Якоби квантовой механики .
Смотрите также
Ссылки
- ^ Палмер, Д. (13 сентября 1997 г.). «Водород во Вселенной». NASA . Архивировано из оригинала 29 октября 2014 г. Получено 23 февраля 2017 г.
- ^ ab Housecroft, Catherine E.; Sharpe, Alan G. (2005). Неорганическая химия (2-е изд.). Pearson Prentice-Hall. стр. 237. ISBN 0130-39913-2.
- ^ Olsen, James; McDonald, Kirk (7 марта 2005 г.). "Classical Lifetime of a Bohr Atom" (PDF) . Joseph Henry Laboratories, Princeton University. Архивировано из оригинала (PDF) 9 сентября 2019 г. . Получено 11 декабря 2015 г. .
- ^ "Вывод уравнений Бора для одноэлектронного атома" (PDF) . Массачусетский университет, Бостон.
- ^ Eite Tiesinga, Peter J. Mohr, David B. Newell и Barry N. Taylor (2019), "The 2018 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 8.0). База данных разработана J. Baker, M. Douma и S. Kotochigova . Доступно по адресу http://physics.nist.gov/constants, Национальный институт стандартов и технологий, Гейтерсберг, Мэриленд 20899. Ссылка на R∞, Ссылка на hcR∞
- ^ "Решение уравнения Шредингера для атома водорода :: Атомная физика :: Веб-пространство Руди Винтера". users.aber.ac.uk . Получено 30 ноября 2020 г. .
- ^ Мессия, Альберт (1999). Квантовая механика . Нью-Йорк: Довер. С. 1136. ISBN 0-486-40924-4.
- ^ LaguerreL. Страница Wolfram Mathematica
- ^ Гриффитс, стр. 152
- ^ Кондон и Шортли (1963). Теория атомных спектров . Лондон: Кембридж. стр. 441.
- ↑ Гриффитс, Гл. 4 стр. 89
- ^ Bransden, BH; Joachain, CJ (1983). Физика атомов и молекул . Longman . стр. Приложение 5. ISBN 0-582-44401-2.
- ^ Зоммерфельд, Арнольд (1919). Atombau und Spektrallinien [ Атомная структура и спектральные линии ]. Брауншвейг: Фридрих Видег и Зон. ISBN 3-87144-484-7.немецкий английский
- ^ Аткинс, Питер; де Паула, Хулио (2006). Физическая химия (8-е изд.). WH Freeman. стр. 349. ISBN 0-7167-8759-8.
- ^ Паули, W (1926). «Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik». Zeitschrift für Physik . 36 (5): 336–363. Бибкод : 1926ZPhy...36..336P. дои : 10.1007/BF01450175. S2CID 128132824.
- ^ Kleinert H. (1968). "Групповая динамика атома водорода" (PDF) . Лекции по теоретической физике, под редакцией WE Brittin и AO Barut, Gordon and Breach, NY 1968 : 427–482.
- ^ Duru IH, Kleinert H. (1979). "Решение интеграла по траектории для атома водорода" (PDF) . Physics Letters B. 84 ( 2): 185–188. Bibcode : 1979PhLB...84..185D. doi : 10.1016/0370-2693(79)90280-6.
- ^ Дуру IH, Кляйнерт Х. (1982). «Квантовая механика H-атома из интегралов по траекториям» (PDF) . Форчр. Физ . 30 (2): 401–435. Бибкод : 1982ForPh..30..401D. дои : 10.1002/prop.19820300802.
Книги
- Гриффитс, Дэвид Дж. (1995). Введение в квантовую механику . Prentice Hall . ISBN 0-13-111892-7.Раздел 4.2 посвящен конкретно атому водорода, но вся глава 4 имеет отношение к делу.
- Kleinert, H. (2009). Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets , 4-е издание, Worldscibooks.com, World Scientific, Сингапур (также доступно онлайн physik.fu-berlin.de)
Внешние ссылки
- Атом водорода и периодическая таблица - Фейнмановские лекции по физике
- Физика атома водорода на Scienceworld











































![{\displaystyle -{\frac {\hbar ^{2}}{2\mu }}\left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \varphi ^{2}}}\right]-{\frac {e^{2}}{4\pi \varepsilon _{0}r}}\пси =E\пси }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed150abb1693ab2493937b669446a54865b9562)





































![{\displaystyle {\begin{aligned}E_{j\,n}={}&-\mu c^{2}\left[1-\left(1+\left[{\frac {\alpha }{nj-{\frac {1}{2}}+{\sqrt {\left(j+{\frac {1}{2}}\right)^{2}-\alpha ^{2}}}}}\right]^{2}\right)^{-1/2}\right]\\\приблизительно {}&-{\frac {\mu c^{2}\alpha ^{2}}{2n^{2}}}\left[1+{\frac {\alpha ^{2}}{n^{2}}}\left({\frac {n}{j+{\frac {1}{2}}}}-{\frac {3}{4}}\right)\right],\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e54f0064eafaeab9e7d8b3e5e41e667a3138a7b)








![{\displaystyle \propto |\psi _{1}\psi _{2}|\cos {[(\omega _{1}-\omega _{2})t]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c419edd50715058a41be3adb8684f2826fe790e9)