Классическая задача центральной силы
| Часть серии статей о |
| Классическая механика |
|---|
В классической механике проблема центральной силы заключается в определении движения частицы в одном центральном потенциальном поле . Центральная сила — это сила (возможно, отрицательная), которая направлена от частицы прямо к фиксированной точке в пространстве, центру, и величина которой зависит только от расстояния объекта до центра. В нескольких важных случаях задача может быть решена аналитически, т. е. в терминах хорошо изученных функций, таких как тригонометрические функции .
Решение этой проблемы важно для классической механики , поскольку многие силы естественного происхождения являются центральными. Примерами служат гравитация и электромагнетизм, описанные законом всемирного тяготения Ньютона и законом Кулона соответственно. Проблема также важна, поскольку некоторые более сложные проблемы классической физики (например, задача двух тел с силами вдоль линии, соединяющей два тела) можно свести к задаче центральной силы. Наконец, решение задачи центральной силы часто дает хорошее начальное приближение истинного движения, как при расчете движения планет в Солнечной системе .
Основы
Суть задачи о центральной силе состоит в определении положения r [примечание 1] частицы, движущейся под действием центральной силы F , либо как функции времени t , либо как функции угла φ относительно центра силы и произвольной оси.
Определение центральной силы

Консервативная центральная сила F имеет два определяющих свойства. [1] Во-первых, она должна двигать частицы либо прямо к фиксированной точке пространства, либо прямо от нее, центра силы, который часто обозначается как O. Другими словами, центральная сила должна действовать вдоль линии, соединяющей O с текущим положением частицы. Во-вторых, консервативная центральная сила зависит только от расстояния r между O и движущейся частицей; она не зависит явно от времени или других дескрипторов положения.
Это двойное определение может быть выражено математически следующим образом. Центр силы O может быть выбран в качестве начала системы координат. Вектор r, соединяющий O с текущим положением частицы, известен как вектор положения . Следовательно, центральная сила должна иметь математическую форму [2] где r — векторная величина | r | (расстояние до центра силы), а r̂ = r /r — соответствующий единичный вектор . Согласно второму закону движения Ньютона , центральная сила F создает параллельное ускорение a, масштабируемое массой m частицы [примечание 2]
Для сил притяжения F ( r ) отрицательна, поскольку она работает на сокращение расстояния r до центра. Наоборот, для сил отталкивания F ( r ) положительна.
Потенциальная энергия
Если центральная сила является консервативной , то величина F ( r ) центральной силы всегда может быть выражена как производная не зависящей от времени функции потенциальной энергии U ( r ) [3]
Таким образом, полная энергия частицы — сумма ее кинетической энергии и потенциальной энергии U — является постоянной; говорят, что энергия сохраняется . Чтобы показать это, достаточно, что работа W, совершаемая силой, зависит только от начального и конечного положений, а не от пути, пройденного между ними.
Эквивалентно, достаточно, чтобы ротор силового поля F был равен нулю; используя формулу для ротора в сферических координатах , поскольку частные производные равны нулю для центральной силы; величина F не зависит от угловых сферических координат θ и φ.
Поскольку скалярный потенциал V ( r ) зависит только от расстояния r до начала координат, он имеет сферическую симметрию . В этом отношении проблема центральной силы аналогична геодезическим Шварцшильда в общей теории относительности и квантово-механическим трактовкам частиц в потенциалах сферической симметрии .
Одномерная задача
Если начальная скорость v частицы совпадает с вектором положения r , то движение навсегда остается на линии, определяемой r . Это следует из того, что сила — а по второму закону Ньютона также и ускорение a — также совпадает с r . Чтобы определить это движение, достаточно решить уравнение
Одним из методов решения является использование закона сохранения полной энергии.
Взяв обратную величину и интегрируя, получаем:
В оставшейся части статьи предполагается, что начальная скорость v частицы не совпадает с вектором положения r , т. е. что вектор момента импульса L = r × m v не равен нулю.
Равномерное круговое движение
Каждая центральная сила может производить равномерное круговое движение при условии, что начальный радиус r и скорость v удовлетворяют уравнению для центростремительной силы
Если это уравнение выполняется в начальные моменты времени, оно будет выполняться и во все последующие моменты времени; частица будет продолжать двигаться по окружности радиуса r со скоростью v вечно.
Связь с классической задачей двух тел

Проблема центральной силы касается идеальной ситуации («задача одного тела»), в которой одна частица притягивается или отталкивается от неподвижной точки O , центра силы. [4] Однако физические силы, как правило, существуют между двумя телами; и по третьему закону Ньютона, если первое тело прикладывает силу ко второму, второе тело прикладывает равную и противоположную силу к первому. Следовательно, оба тела ускоряются, если между ними присутствует сила; нет совершенно неподвижного центра силы. Однако, если одно тело в подавляющем большинстве массивнее другого, его ускорением относительно другого можно пренебречь; центр более массивного тела можно рассматривать как приблизительно фиксированный. [5] Например, Солнце в подавляющем большинстве массивнее планеты Меркурий; следовательно, Солнце можно аппроксимировать как неподвижный центр силы, сводя проблему к движению Меркурия в ответ на силу, приложенную Солнцем. В действительности, однако, Солнце также движется (хотя и незначительно) в ответ на силу, приложенную планетой Меркурий.

Однако такие приближения не нужны. Законы движения Ньютона позволяют преобразовать любую классическую задачу двух тел в соответствующую точную задачу одного тела. [6] Чтобы продемонстрировать это, пусть x 1 и x 2 будут положениями двух частиц, а r = x 1 − x 2 будет их относительным положением. Тогда, по второму закону Ньютона,
Окончательное уравнение вытекает из третьего закона Ньютона ; сила второго тела, действующая на первое тело ( F 21 ), равна и противоположна силе первого тела, действующей на второе ( F 12 ). Таким образом, уравнение движения для r можно записать в виде где - приведенная масса
Как частный случай, задачу о двух телах, взаимодействующих посредством центральной силы, можно свести к задаче о центральной силе одного тела.
Качественные свойства
Плоское движение

Движение частицы под действием центральной силы F всегда остается в плоскости, определяемой ее начальным положением и скоростью. [7] Это можно увидеть с помощью симметрии. Поскольку положение r , скорость v и сила F лежат в одной плоскости, никогда не существует ускорения, перпендикулярного этой плоскости, поскольку это нарушило бы симметрию между «над» плоскостью и «под» плоскостью.
Чтобы продемонстрировать это математически, достаточно показать, что момент импульса частицы постоянен. Этот момент импульса L определяется уравнением , где m — масса частицы, а p — ее линейный импульс . В этом уравнении символ × обозначает векторное векторное произведение , а не умножение. Поэтому вектор момента импульса L всегда перпендикулярен плоскости, определяемой вектором положения частицы r и вектором скорости v . [примечание 3]
В общем случае скорость изменения момента импульса L равна чистому крутящему моменту r × F [8]
Первый член m v × v всегда равен нулю, поскольку векторное векторное произведение всегда равно нулю для любых двух векторов, направленных в одном или противоположных направлениях. Однако, когда F является центральной силой, оставшийся член r × F также равен нулю, поскольку векторы r и F направлены в одном или противоположных направлениях. Следовательно, вектор углового момента L постоянен. Тогда
Следовательно, положение частицы r (и, следовательно, скорость v ) всегда лежит в плоскости, перпендикулярной L. [ 9]
Полярные координаты

Поскольку движение плоское, а сила радиальная, принято переходить к полярным координатам . [9] В этих координатах радиус-вектор r представлен через радиальное расстояние r и азимутальный угол φ .
Взяв первую производную по времени, получаем вектор скорости частицы v
Аналогично, вторая производная положения частицы r равна ее ускорению a
Скорость v и ускорение a можно выразить через радиальный и азимутальный единичные векторы. Радиальный единичный вектор получается путем деления вектора положения r на его величину r , как описано выше
Азимутальный единичный вектор определяется как [примечание 4]
Таким образом, скорость можно записать как, тогда как ускорение равно
Удельный момент импульса

Поскольку F = m a по второму закону движения Ньютона и поскольку F является центральной силой, то только радиальная составляющая ускорения a может быть ненулевой; угловая составляющая a φ должна быть равна нулю.
Поэтому,
Это выражение в скобках обычно обозначается h
что равно скорости v, умноженной на r ⊥ , компоненту радиуса-вектора, перпендикулярного скорости. h — это величина удельного момента импульса , поскольку она равна величине L момента импульса, деленной на массу m частицы.
Для краткости угловую скорость иногда записывают как ω.
Однако не следует предполагать, что ω постоянна. Поскольку h постоянна, ω изменяется с радиусом r согласно формуле [10]
Поскольку h постоянна, а r 2 положителен, угол φ изменяется монотонно в любой задаче с центральной силой, либо непрерывно увеличиваясь ( h положительна), либо непрерывно уменьшаясь ( h отрицательна). [11]
Постоянная площадная скорость

Величина h также равна удвоенной скорости площади , которая является скоростью, с которой площадь выметается частицей относительно центра. [12] Таким образом, скорость площади постоянна для частицы, на которую действует любая центральная сила; это второй закон Кеплера . [13] И наоборот, если движение под действием консервативной силы F является плоским и имеет постоянную скорость площади для всех начальных условий радиуса r и скорости v , то азимутальное ускорение a φ всегда равно нулю. Следовательно, по второму закону Ньютона, F = m a , сила является центральной силой.
Постоянство скорости площади можно проиллюстрировать равномерным круговым и линейным движением. При равномерном круговом движении частица движется с постоянной скоростью v по окружности радиуса r . Поскольку угловая скорость ω = v / r постоянна, площадь, выметенная за время Δ t, равна ω r 2 Δ t ; следовательно, равные площади выметаются за равное время Δ t . При равномерном линейном движении (т. е. движении в отсутствие силы, по первому закону движения Ньютона) частица движется с постоянной скоростью, то есть с постоянной скоростью v вдоль линии. За время Δ t частица выметает площадь 1 ⁄ 2 v Δ tr ⊥ ( параметр удара ). [примечание 5] Расстояние r ⊥ не изменяется по мере движения частицы вдоль линии; оно представляет собой расстояние наибольшего приближения линии к центру O ( параметр удара ). Поскольку скорость v также неизменна, площадная скорость 1 ⁄ 2 vr ⊥ является константой движения; частица заметает равные площади за равное время.

Эквивалентное параллельное силовое поле
Путем преобразования переменных [14] любую задачу с центральной силой можно преобразовать в эквивалентную задачу с параллельной силой. [примечание 6] Вместо обычных декартовых координат x и y определяются две новые переменные положения ξ = x / y и η = 1/ y , а также новая временная координата τ.
Соответствующие уравнения движения для ξ и η имеют вид
Поскольку скорость изменения ξ постоянна, ее вторая производная равна нулю.
Поскольку это ускорение в направлении ξ и поскольку F = ma по второму закону Ньютона, то отсюда следует, что сила в направлении ξ равна нулю. Следовательно, сила действует только вдоль направления η , что является критерием для задачи о параллельных силах. Явно, ускорение в направлении η равно , поскольку ускорение в направлении y равно
Здесь F y обозначает y -компоненту центральной силы, а y / r равен косинусу угла между осью y и радиальным вектором r .
Общее решение
Уравнение Бине
Поскольку центральная сила F действует только вдоль радиуса, то ненулевой является только радиальная составляющая ускорения. Согласно второму закону движения Ньютона, величина F равна массе m частицы, умноженной на величину ее радиального ускорения [15]
Это уравнение имеет интеграционный коэффициент
Интеграция урожайности
Если h не равно нулю, независимую переменную можно изменить с t на ϕ [16], что даст новое уравнение движения [17]
Сделав замену переменных на обратный радиус u = 1/ r [17], получим
| 1 |
где C — константа интегрирования, а функция G ( u ) определяется как
Это уравнение становится квазилинейным при дифференцировании по ϕ
Это известно как уравнение Бине . Интегрирование ( 1 ) дает решение для ϕ [18] , где ϕ 0 — еще одна константа интегрирования. Задача центральной силы называется «интегрируемой», если это окончательное интегрирование может быть решено в терминах известных функций.
Орбита частицы
Возьмите скалярное произведение второго закона движения Ньютона со скоростью частицы, где сила получается из потенциальной энергии, дает где предполагается суммирование по пространственному декартову индексу , и мы использовали тот факт, что и использовали цепное правило . Перестановка Член в скобках с левой стороны является константой, обозначим это как , полная механическая энергия. Очевидно, что это сумма кинетической энергии и потенциальной энергии. [19]
Кроме того, если потенциал центральный, и поэтому сила направлена вдоль радиального направления. В этом случае перекрестное произведение второго закона движения Ньютона с вектором положения частицы должно исчезнуть, поскольку перекрестное произведение двух параллельных векторов равно нулю: но (перекрестное произведение параллельных векторов), поэтому Член в скобках в левой части является константой, обозначим это как угловой момент, В частности, в полярных координатах, или Далее, , поэтому уравнение энергии может быть упрощено с угловым моментом как Это указывает на то, что угловой момент вносит вклад в эффективную потенциальную энергию [20] Решите это уравнение для которого можно преобразовать в производную по азимутальному углу как Это разделяемое дифференциальное уравнение первого порядка. Интегрирование и дает формулу [21]
Изменение переменной интегрирования на обратный радиус дает интеграл [22] , который выражает указанные выше константы C = 2 mE tot / L 2 и G ( u ) = 2 mU (1/ u )/ L 2 через полную энергию E tot и потенциальную энергию U ( r ).
Точки поворота и замкнутые орбиты
Скорость изменения r равна нулю, когда эффективная потенциальная энергия равна полной энергии [23]
Точки, в которых это уравнение выполняется, называются точками поворота . [23] Орбита по обе стороны от точки поворота симметрична; другими словами, если азимутальный угол определен таким образом, что φ = 0 в точке поворота, то орбита одинакова в противоположных направлениях, r ( φ ) = r (− φ ). [24]
Если имеются две точки поворота, такие, что радиус r ограничен между r min и r max , то движение заключено в кольце этих радиусов. [23] Поскольку радиус изменяется от одной точки поворота к другой, изменение азимутального угла φ равно [23]
Орбита замкнется сама на себя [примечание 7] при условии, что Δφ равно рациональной дроби 2π , т.е. [23] где m и n — целые числа. В этом случае радиус колеблется ровно m раз, в то время как азимутальный угол φ совершает ровно n оборотов. Однако в общем случае Δφ/2π не будет таким рациональным числом , и, таким образом, орбита не будет замкнутой. В этом случае частица в конечном итоге пройдет произвольно близко к каждой точке внутри кольца. Два типа центральной силы всегда создают замкнутые орбиты: F ( r ) = αr ( линейная сила) и F ( r ) = α/ r2 ( закон обратных квадратов ). Как показал Бертран, эти две центральные силы являются единственными, которые гарантируют замкнутые орбиты. [25]
В общем случае, если угловой момент L не равен нулю, то член L 2 /2 mr 2 препятствует падению частицы в начало координат, если только эффективная потенциальная энергия не стремится к отрицательной бесконечности в пределе r, стремящегося к нулю. [26] Поэтому, если имеется одна точка поворота, орбита, как правило, стремится к бесконечности; точка поворота соответствует точке минимального радиуса.
Конкретные решения
проблема Кеплера

В классической физике многие важные силы подчиняются закону обратных квадратов, например, гравитация или электростатика . Общая математическая форма таких центральных сил с обратными квадратами — константа , которая отрицательна для силы притяжения и положительна для силы отталкивания.
Этот частный случай классической проблемы центральной силы называется проблемой Кеплера . Для силы, обратной квадрату, уравнение Бине, полученное выше, является линейным
Решение этого уравнения есть которое показывает, что орбита является коническим сечением эксцентриситета e ; здесь φ 0 — начальный угол, а центр силы находится в фокусе конического сечения. Используя формулу половинного угла для синуса , это решение можно также записать как

где u 1 и u 2 — константы, причем u 2 больше u 1. Две версии решения связаны уравнениями и
Так как функция sin 2 всегда больше нуля, u 2 является наибольшим возможным значением u и обратным наименьшему возможному значению r , т. е. расстоянию наибольшего сближения ( перицентру ). Так как радиальное расстояние r не может быть отрицательным числом, то и обратное ему u ; следовательно, u 2 должно быть положительным числом. Если u 1 также положительно, то это наименьшее возможное значение u , которое соответствует наибольшему возможному значению r , расстоянию наибольшего сближения ( апоцентру ). Если u 1 равно нулю или отрицательно, то наименьшее возможное значение u равно нулю (орбита стремится к бесконечности); в этом случае единственные соответствующие значения φ — это те, которые делают u положительным.
Для силы притяжения (α < 0) орбита представляет собой эллипс , гиперболу или параболу , в зависимости от того, является ли u 1 положительным, отрицательным или нулевым соответственно; это соответствует эксцентриситету e меньше единицы, больше единицы или равному единице. Для силы отталкивания (α > 0) u 1 должен быть отрицательным, так как u 2 по определению положительно, а их сумма отрицательна; следовательно, орбита представляет собой гиперболу. Естественно, если сила отсутствует (α = 0), орбита представляет собой прямую линию.
Центральные силы с точными решениями
Уравнение Бине для u ( φ ) может быть решено численно для почти любой центральной силы F (1/ u ). Однако только несколько сил приводят к формулам для u в терминах известных функций. Как выведено выше, решение для φ может быть выражено как интеграл по u
Задача с центральной силой называется «интегрируемой», если эта интеграция может быть решена в терминах известных функций.
Если сила является степенным законом, т. е. если F ( r ) = α r n , то u может быть выражена в терминах круговых функций и/или эллиптических функций, если n равно 1, -2, -3 (круговые функции) и -7, -5, -4, 0, 3, 5, -3/2, -5/2, -1/3, -5/3 и -7/3 (эллиптические функции). [27] Аналогично, только шесть возможных линейных комбинаций степенных законов дают решения в терминах круговых и эллиптических функций [28] [29]
Следующие особые случаи первых двух типов сил всегда приводят к круговым функциям.
Этот особый случай был упомянут Ньютоном в следствии 1 к предложению VII «Начал», как сила, подразумеваемая круговыми орбитами, проходящими через точку притяжения.
Вращающиеся орбиты
Член r −3 встречается во всех законах силы выше, указывая на то, что добавление силы обратного куба не влияет на разрешимость задачи в терминах известных функций. Ньютон показал, что с корректировками начальных условий добавление такой силы не влияет на радиальное движение частицы, но умножает ее угловое движение на постоянный коэффициент k . Расширение теоремы Ньютона было обнаружено в 2000 году Магомедом и Ваудой. [29]
Предположим, что частица движется под действием произвольной центральной силы F 1 ( r ), и пусть ее радиус r и азимутальный угол φ будут обозначены как r ( t ) и φ 1 ( t ) как функции времени t . Теперь рассмотрим вторую частицу с той же массой m , которая разделяет то же радиальное движение r ( t ), но чья угловая скорость в k раз больше, чем у первой частицы. Другими словами, азимутальные углы двух частиц связаны уравнением φ 2 ( t ) = k φ 1 ( t ). Ньютон показал, что сила, действующая на вторую частицу, равна силе F 1 ( r ), действующей на первую частицу, плюс обратная кубическая центральная сила [30] , где L 1 — величина углового момента первой частицы .
Если k 2 больше единицы, F 2 − F 1 — отрицательное число; таким образом, добавленная сила обратного куба является притягивающей . Наоборот, если k 2 меньше единицы, F 2 − F 1 — положительное число; добавленная сила обратного куба является отталкивающей . Если k — целое число, например 3, то орбита второй частицы называется гармоникой орбиты первой частицы; напротив, если k — обратное целое число, например 1 ⁄ 3 , то вторая орбита называется субгармоникой первой орбиты.
Историческое развитие

Вывод Ньютона
Классическая проблема центральной силы была решена геометрически Исааком Ньютоном в его Philosophiæ Naturalis Principia Mathematica , в котором Ньютон ввел свои законы движения . Ньютон использовал эквивалент интегрирования скачком, чтобы преобразовать непрерывное движение в дискретное, так что можно было бы применять геометрические методы. При таком подходе положение частицы рассматривается только в равномерно разнесенных временных точках. Для иллюстрации частица на рисунке 10 находится в точке A в момент времени t = 0, в точке B в момент времени t = Δ t , в точке C в момент времени t = 2Δ t и так далее для всех моментов времени t = n Δ t , где n — целое число. Предполагается, что скорость постоянна между этими временными точками. Таким образом, вектор r AB = r B − r A равен Δ t, умноженному на вектор скорости v AB (красная линия), тогда как r BC = r C − r B равен v BC Δ t (синяя линия). Поскольку скорость постоянна между точками, предполагается, что сила действует мгновенно в каждом новом положении; например, сила, действующая на частицу в точке B, мгновенно изменяет скорость с v AB на v BC . Вектор разности Δ r = r BC − r AB равен Δ v Δ t (зеленая линия), где Δ v = v BC − v AB — это изменение скорости в результате действия силы в точке B . Поскольку ускорение a параллельно Δ v и поскольку F = m a , сила F должна быть параллельна Δ v и Δ r . Если F — центральная сила, она должна быть параллельна вектору r B из центра O в точку B (штриховая зеленая линия); в этом случае Δ r также параллелен r B.
Если в точке B не действует никакая сила , скорость не меняется, и частица прибывает в точку K в момент времени t = 2Δ t . Площади треугольников OAB и OBK равны, поскольку они имеют одинаковое основание ( r AB ) и высоту ( r ⊥ ). Если Δ r параллельна r B , треугольники OBK и OBC также равны, поскольку они имеют одинаковое основание ( r B ), а высота не меняется. В этом случае площади треугольников OAB и OBC одинаковы, и частица заметает равные площади за одинаковое время. И наоборот, если площади всех таких треугольников равны, то Δ r должна быть параллельна r B , из чего следует, что F является центральной силой. Таким образом, частица заметает равные площади за одинаковое время тогда и только тогда, когда F является центральной силой.
Альтернативные выводы уравнений движения
Лагранжева механика
Формула для радиальной силы может быть также получена с использованием механики Лагранжа . В полярных координатах лагранжиан L отдельной частицы в потенциальном поле энергии U ( r ) определяется как
Тогда уравнения движения Лагранжа принимают вид, поскольку величина F ( r ) радиальной силы равна отрицательной производной потенциальной энергии U ( r ) в радиальном направлении.
Гамильтонова механика
Формула радиальной силы может быть также выведена с использованием гамильтоновой механики . В полярных координатах гамильтониан можно записать как
Поскольку азимутальный угол φ не появляется в гамильтониане, его сопряженный импульс p φ является константой движения. Этот сопряженный импульс является величиной L углового момента, как показано в гамильтоновом уравнении движения для φ
Соответствующее уравнение движения для r имеет вид
Взяв вторую производную от r по времени и используя уравнение движения Гамильтона для p r, получаем уравнение радиальной силы
Уравнение Гамильтона-Якоби
Орбитальное уравнение может быть получено непосредственно из уравнения Гамильтона-Якоби . [31] Принимая радиальное расстояние r и азимутальный угол φ в качестве координат, уравнение Гамильтона-Якоби для задачи центральной силы можно записать , где S = S φ ( φ ) + S r ( r ) − E tot t — главная функция Гамильтона , а E tot и t представляют собой полную энергию и время соответственно. Это уравнение может быть решено путем последовательного интегрирования обыкновенных дифференциальных уравнений , начиная с уравнения φ , где p φ — константа движения, равная величине углового момента L . Таким образом, S φ (φ) = L φ и уравнение Гамильтона-Якоби становится
Интегрирование этого уравнения для S r дает
Взяв производную от S по L, получаем орбитальное уравнение, выведенное выше:
Смотрите также
- Геодезические линии Шварцшильда , аналог в общей теории относительности
- Частица в сферически симметричном потенциале , аналог в квантовой механике
- Водородоподобный атом , задача Кеплера в квантовой механике
- Обратный квадрат потенциала
Примечания
- ^ В этой статье жирный шрифт используется для обозначения того, что такие величины, как r и F, являются векторами , тогда как обычные числа пишутся курсивом. Вкратце, вектор v — это величина, имеющая величину v (также пишется | v |) и направление. Векторы часто определяются их компонентами. Например, вектор положения r = ( x , y ) в декартовых координатах описывается как упорядоченная пара его координат x и y .
- ^ В этой статье нотация Ньютона для производных («точечная нотация») иногда используется для того, чтобы сделать формулы более удобными для чтения; она не имеет другого значения. В этой нотации одна точка над переменной обозначает ее первую производную по времени, например, Аналогично, две точки над переменной обозначают ее вторую производную по времени, например,
- ^ Если a и b — трехмерные векторы, то их векторное произведение c = a × b всегда перпендикулярно плоскости, определяемой a и b .
- ^ Эту формулу для азимутального единичного вектора можно проверить расчетом; его величина равна единице , а его скалярное произведение на r равно нулю. Следовательно, это единичный вектор, перпендикулярный радиальному вектору r .
- ^ Площадь треугольника равна половине основания, умноженного на его высоту. В этом случае основание задается как v Δ t , а высота равна ударному параметру r ⊥ .
- ^ Задача с параллельными силами — это задача, в которой сила равна нулю вдоль одного направления.
- ^ Замкнутая орбита — это та, которая возвращается в исходное положение через конечное время с точно такой же скоростью. Следовательно, она выполняет точно такое же движение снова и снова.
Ссылки
- ^ Гольдштейн, с. 71; Ландау и Лифшиц, с. 30; Зоммерфельд, с. 39; Саймон, с. 121.
- ↑ Ландау и Лифшиц, стр. 30; Саймон, стр. 121.
- ↑ Гольдштейн, стр. 4; Ландау и Лифшиц, стр. 30; Саймон, стр. 122.
- ↑ Гольдштейн, стр. 71; Ландау и Лифшиц, стр. 30; Уиттекер, стр. 77.
- ^ Зоммерфельд, с. 39; Саймон, с. 123.
- ↑ Гольдштейн, стр. 70–71; Ландау и Лифшиц, стр. 29; Саймон, стр. 182–185; Уиттекер, стр. 76–77.
- ↑ Гольдштейн, стр. 72; Ландау и Лифшиц, стр. 30; Уиттекер, стр. 77.
- ↑ Гольдштейн, стр. 2–3, 6–7.
- ^ ab Goldstein, стр. 72.
- ^ Гольдштейн, с. 73; Ландау и Лифшиц, стр. 30–31; Зоммерфельд, стр. 39–40; Саймон, стр. 124, 127.
- ↑ Ландау и Лифшиц, стр. 31.
- ^ Гольдштейн, с. 73; Ландау и Лифшиц, стр. 30–31; Зоммерфельд, стр. 36, 39; Саймон, стр. 127–128.
- ^ Гольдштейн, с. 73; Ландау и Лифшиц, с. 31; Зоммерфельд, с. 39; Саймон, с. 135.
- ↑ Уиттекер, стр. 93–94.
- ↑ Гольдштейн, стр. 73.
- ↑ Гольдштейн, стр. 75, 86.
- ^ ab Goldstein, стр. 86.
- ↑ Уиттекер, стр. 80‒81.
- ↑ Гольдштейн, стр. 4.
- ↑ Гольдштейн, стр. 76–82.
- ↑ Гольдштейн, стр. 87.
- ↑ Гольдштейн, стр. 88.
- ^ abcde Ландау и Лифшиц, стр. 32.
- ↑ Ландау и Лифшиц, стр. 32–33.
- ↑ Гольдштейн, стр. 601–605.
- ↑ Ландау и Лифшиц, стр. 33.
- ↑ Уиттекер, стр. 80–95.
- ^ Broucke R (1980). «Заметки о центральной силе r n ». Астрофизика и космическая наука . 72 (1): 33– 53. Bibcode : 1980Ap&SS..72...33B. doi : 10.1007/BF00642162. S2CID 123025228.
- ^ ab Mahomed FM, Vawda F (2000). "Применение симметрий к проблемам центральной силы". Нелинейная динамика . 21 (4): 307– 315. Bibcode :2000NonDy..21..307M. doi :10.1023/A:1008317327402. S2CID 116319304.
- ↑ Ньютон, Principia , раздел IX книги I, предложения 43–45, стр. 135–147.
- ↑ Гольдштейн, стр. 454–457; Ландау и Лифшиц, стр. 149–151; Мизнер, Торн и Уилер, стр. 644–649; Зоммерфельд, стр. 235–238.
Библиография
- Goldstein, H. (1980). Классическая механика (2-е изд.). Reading, MA: Addison-Wesley. ISBN 0-201-02918-9.
- Ландау, Л. Д. и Лифшиц, Э. М. (1976). Механика . Курс теоретической физики (3-е изд.). Нью-Йорк: Pergamon Press. ISBN 0-08-029141-4.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Misner, CW , Thorne, K. и Wheeler, JA (1973). Гравитация . Сан-Франциско: WH Freeman. ISBN 978-0-7167-0344-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Зоммерфельд, А. (1970). Механика . Лекции по теоретической физике . Т. I (4-е изд.). Нью-Йорк: Academic Press. ISBN 978-0-12-654670-5.
- Symon KR (1971). Механика (3-е изд.). Reading, Massachusetts: Addison-Wesley. ISBN 0-201-07392-7.
- Уиттекер, ET (1937). Трактат об аналитической динамике частиц и твердых тел с введением в задачу трех тел (4-е изд.). Нью-Йорк: Dover Publications. ISBN 978-0-521-35883-5.
Внешние ссылки
- Задачи двух тел с центральной силой, Д. Э. Гэри из Технологического института Нью-Джерси
- Движение в поле центральной силы. Архивировано 21 сентября 2018 г. в Wayback Machine А. Бризардом из колледжа Святого Михаила.
- Движение под действием центральной силы, автор GW Collins, II, Университет Кейс Вестерн Резерв
- Видеолекция WHG Lewin из Массачусетского технологического института

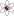





































![{\displaystyle {\begin{aligned}F(r)\,dr&=F(r){\frac {dr}{dt}}\,dt\\&=m\left({\frac {dr}{dt}}{\frac {d^{2}r}{dt^{2}}}-{\frac {h^{2}}{r^{3}}}{\frac {dr}{dt}}\right)\,dt\\&={\frac {m}{2}}\,d\left[\left({\frac {dr}{dt}}\right)^{2}+\left({\frac {h}{r}}\right)^{2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26e59b4b76c0a42cc89c842afa0563c4a6d2ff20)
![{\displaystyle \int ^{r}F(r)\,dr={\frac {m}{2}}\left[\left({\frac {dr}{dt}}\right)^{2}+\left({\frac {h}{r}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e10a467bb0dce3d92b1826c73e13f580c30db95)

![{\displaystyle \int ^{r}F(r)\,dr={\frac {mh^{2}}{2}}\left[\left(-{\frac {1}{r^{2}}}{\frac {dr}{d\varphi }}\right)^{2}+\left({\frac {1}{r}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6fdd7a0a24825cd61f57b5f2a34446ac449f6b8)



































![{\displaystyle u(\varphi)=- {\frac {\alpha }{mh^{2}}}\left[1+e\cos \left(\varphi -\varphi _{0}\right)\right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d346a044e3603002a2d0a12ae4bf88984c4e7d7)































