В тригонометрии тригонометрические тождества — это равенства , которые включают тригонометрические функции и верны для каждого значения встречающихся переменных, для которых определены обе стороны равенства. Геометрически это тождества , включающие определенные функции одного или нескольких углов . Они отличаются от тождеств треугольников , которые являются тождествами, потенциально включающими углы, но также включающими длины сторон или другие длины треугольника .
Эти тождества полезны всякий раз, когда выражения, включающие тригонометрические функции, необходимо упростить. Важным применением является интегрирование нетригонометрических функций: распространенный метод включает в себя сначала использование правила подстановки с тригонометрической функцией , а затем упрощение полученного интеграла с помощью тригонометрического тождества.
Пифагорейские тождества Тригонометрические функции и их обратные величины на единичной окружности. Все прямоугольные треугольники подобны, т. е. соотношения между их соответствующими сторонами одинаковы. Для sin, cos и tan единичный радиус образует гипотенузу треугольника, который их определяет. Обратные тождества возникают как соотношения сторон в треугольниках, где эта единичная линия больше не является гипотенузой. Треугольник, закрашенный синим цветом, иллюстрирует тождество , а красный треугольник показывает, что . 1 + детская кроватка 2 θ = csc 2 θ {\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta } загар 2 θ + 1 = сек 2 θ {\displaystyle \tan ^{2}\theta +1=\sec ^{2}\theta } Основное соотношение между синусом и косинусом определяется тождеством Пифагора:
грех 2 θ + потому что 2 θ = 1 , {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}
где средства и средства грех 2 θ {\displaystyle \sin^{2}\theta} ( грех θ ) 2 {\displaystyle (\sin \theta )^{2}} потому что 2 θ {\displaystyle \cos ^{2}\theta } ( потому что θ ) 2 . {\displaystyle (\cos \theta)^{2}.}
Это можно рассматривать как версию теоремы Пифагора , и следует из уравнения для единичной окружности . Это уравнение можно решить либо относительно синуса, либо относительно косинуса: х 2 + у 2 = 1 {\displaystyle x^{2}+y^{2}=1}
грех θ = ± 1 − потому что 2 θ , потому что θ = ± 1 − грех 2 θ . {\displaystyle {\begin{aligned}\sin \theta &=\pm {\sqrt {1-\cos ^{2}\theta }},\\\cos \theta &=\pm {\sqrt {1-\sin ^{2}\theta }}.\end{aligned}}}
где знак зависит от квадранта θ . {\displaystyle \тета .}
Разделив это тождество на , или на оба, получим следующие тождества: грех 2 θ {\displaystyle \sin^{2}\theta} потому что 2 θ {\displaystyle \cos ^{2}\theta } 1 + детская кроватка 2 θ = csc 2 θ 1 + загар 2 θ = сек 2 θ сек 2 θ + csc 2 θ = сек 2 θ csc 2 θ {\displaystyle {\begin{aligned}&1+\cot ^{2}\theta =\csc ^{2}\theta \\&1+\tan ^{2}\theta =\sec ^{2}\theta \\&\sec ^{2}\theta +\csc ^{2}\theta =\sec ^{2}\theta \csc ^{2}\theta \end{aligned}}}
Используя эти тождества, можно выразить любую тригонометрическую функцию через любую другую ( с точностью до знака плюс или минус):
Каждая тригонометрическая функция через каждую из пяти других. [1] с точки зрения sin θ {\displaystyle \sin \theta } csc θ {\displaystyle \csc \theta } cos θ {\displaystyle \cos \theta } sec θ {\displaystyle \sec \theta } tan θ {\displaystyle \tan \theta } cot θ {\displaystyle \cot \theta } sin θ = {\displaystyle \sin \theta =} sin θ {\displaystyle \sin \theta } 1 csc θ {\displaystyle {\frac {1}{\csc \theta }}} ± 1 − cos 2 θ {\displaystyle \pm {\sqrt {1-\cos ^{2}\theta }}} ± sec 2 θ − 1 sec θ {\displaystyle \pm {\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}} ± tan θ 1 + tan 2 θ {\displaystyle \pm {\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}} ± 1 1 + cot 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1+\cot ^{2}\theta }}}} csc θ = {\displaystyle \csc \theta =} 1 sin θ {\displaystyle {\frac {1}{\sin \theta }}} csc θ {\displaystyle \csc \theta } ± 1 1 − cos 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\cos ^{2}\theta }}}} ± sec θ sec 2 θ − 1 {\displaystyle \pm {\frac {\sec \theta }{\sqrt {\sec ^{2}\theta -1}}}} ± 1 + tan 2 θ tan θ {\displaystyle \pm {\frac {\sqrt {1+\tan ^{2}\theta }}{\tan \theta }}} ± 1 + cot 2 θ {\displaystyle \pm {\sqrt {1+\cot ^{2}\theta }}} cos θ = {\displaystyle \cos \theta =} ± 1 − sin 2 θ {\displaystyle \pm {\sqrt {1-\sin ^{2}\theta }}} ± csc 2 θ − 1 csc θ {\displaystyle \pm {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}} cos θ {\displaystyle \cos \theta } 1 sec θ {\displaystyle {\frac {1}{\sec \theta }}} ± 1 1 + tan 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1+\tan ^{2}\theta }}}} ± cot θ 1 + cot 2 θ {\displaystyle \pm {\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}} sec θ = {\displaystyle \sec \theta =} ± 1 1 − sin 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\sin ^{2}\theta }}}} ± csc θ csc 2 θ − 1 {\displaystyle \pm {\frac {\csc \theta }{\sqrt {\csc ^{2}\theta -1}}}} 1 cos θ {\displaystyle {\frac {1}{\cos \theta }}} sec θ {\displaystyle \sec \theta } ± 1 + tan 2 θ {\displaystyle \pm {\sqrt {1+\tan ^{2}\theta }}} ± 1 + cot 2 θ cot θ {\displaystyle \pm {\frac {\sqrt {1+\cot ^{2}\theta }}{\cot \theta }}} tan θ = {\displaystyle \tan \theta =} ± sin θ 1 − sin 2 θ {\displaystyle \pm {\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}} ± 1 csc 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}} ± 1 − cos 2 θ cos θ {\displaystyle \pm {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}} ± sec 2 θ − 1 {\displaystyle \pm {\sqrt {\sec ^{2}\theta -1}}} tan θ {\displaystyle \tan \theta } 1 cot θ {\displaystyle {\frac {1}{\cot \theta }}} cot θ = {\displaystyle \cot \theta =} ± 1 − sin 2 θ sin θ {\displaystyle \pm {\frac {\sqrt {1-\sin ^{2}\theta }}{\sin \theta }}} ± csc 2 θ − 1 {\displaystyle \pm {\sqrt {\csc ^{2}\theta -1}}} ± cos θ 1 − cos 2 θ {\displaystyle \pm {\frac {\cos \theta }{\sqrt {1-\cos ^{2}\theta }}}} ± 1 sec 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\sec ^{2}\theta -1}}}} 1 tan θ {\displaystyle {\frac {1}{\tan \theta }}} cot θ {\displaystyle \cot \theta }
Рассматривая единичную окружность, можно установить следующие свойства тригонометрических функций.
Размышления Преобразование координат ( a , b ) при смещении угла отражения с шагом α {\displaystyle \alpha } π 4 {\displaystyle {\frac {\pi }{4}}} Когда направление евклидова вектора представлено углом, это угол, определяемый свободным вектором (начинающимся в начале координат) и положительным единичным вектором. То же самое понятие может быть применено к линиям в евклидовом пространстве, где угол определяется параллельной данной линии, проходящей через начало координат и положительную ось. Если линия (вектор) с направлением отражается относительно линии с направлением, то угол направления этой отраженной линии (вектора) имеет значение θ , {\displaystyle \theta ,} x {\displaystyle x} x {\displaystyle x} θ {\displaystyle \theta } α , {\displaystyle \alpha ,} θ ′ {\displaystyle \theta ^{\prime }} θ ′ = 2 α − θ . {\displaystyle \theta ^{\prime }=2\alpha -\theta .}
Значения тригонометрических функций этих углов для конкретных углов удовлетворяют простым тождествам: они либо равны, либо имеют противоположные знаки, либо используют дополнительную тригонометрическую функцию. Они также известны как формулы редукции . [2] θ , θ ′ {\displaystyle \theta ,\;\theta ^{\prime }} α {\displaystyle \alpha }
θ {\displaystyle \theta } [3] четно/нечетных тождествах α = 0 {\displaystyle \alpha =0} θ {\displaystyle \theta } α = π 4 {\displaystyle \alpha ={\frac {\pi }{4}}} θ {\displaystyle \theta } α = π 2 {\displaystyle \alpha ={\frac {\pi }{2}}} θ {\displaystyle \theta } α = 3 π 4 {\displaystyle \alpha ={\frac {3\pi }{4}}} θ {\displaystyle \theta } сравнении с α = π {\displaystyle \alpha =\pi } α = 0 {\displaystyle \alpha =0} sin ( − θ ) = − sin θ {\displaystyle \sin(-\theta )=-\sin \theta } sin ( π 2 − θ ) = cos θ {\displaystyle \sin \left({\tfrac {\pi }{2}}-\theta \right)=\cos \theta } sin ( π − θ ) = + sin θ {\displaystyle \sin(\pi -\theta )=+\sin \theta } sin ( 3 π 2 − θ ) = − cos θ {\displaystyle \sin \left({\tfrac {3\pi }{2}}-\theta \right)=-\cos \theta } sin ( 2 π − θ ) = − sin ( θ ) = sin ( − θ ) {\displaystyle \sin(2\pi -\theta )=-\sin(\theta )=\sin(-\theta )} cos ( − θ ) = + cos θ {\displaystyle \cos(-\theta )=+\cos \theta } cos ( π 2 − θ ) = sin θ {\displaystyle \cos \left({\tfrac {\pi }{2}}-\theta \right)=\sin \theta } cos ( π − θ ) = − cos θ {\displaystyle \cos(\pi -\theta )=-\cos \theta } cos ( 3 π 2 − θ ) = − sin θ {\displaystyle \cos \left({\tfrac {3\pi }{2}}-\theta \right)=-\sin \theta } cos ( 2 π − θ ) = + cos ( θ ) = cos ( − θ ) {\displaystyle \cos(2\pi -\theta )=+\cos(\theta )=\cos(-\theta )} tan ( − θ ) = − tan θ {\displaystyle \tan(-\theta )=-\tan \theta } tan ( π 2 − θ ) = cot θ {\displaystyle \tan \left({\tfrac {\pi }{2}}-\theta \right)=\cot \theta } tan ( π − θ ) = − tan θ {\displaystyle \tan(\pi -\theta )=-\tan \theta } tan ( 3 π 2 − θ ) = + cot θ {\displaystyle \tan \left({\tfrac {3\pi }{2}}-\theta \right)=+\cot \theta } tan ( 2 π − θ ) = − tan ( θ ) = tan ( − θ ) {\displaystyle \tan(2\pi -\theta )=-\tan(\theta )=\tan(-\theta )} csc ( − θ ) = − csc θ {\displaystyle \csc(-\theta )=-\csc \theta } csc ( π 2 − θ ) = sec θ {\displaystyle \csc \left({\tfrac {\pi }{2}}-\theta \right)=\sec \theta } csc ( π − θ ) = + csc θ {\displaystyle \csc(\pi -\theta )=+\csc \theta } csc ( 3 π 2 − θ ) = − sec θ {\displaystyle \csc \left({\tfrac {3\pi }{2}}-\theta \right)=-\sec \theta } csc ( 2 π − θ ) = − csc ( θ ) = csc ( − θ ) {\displaystyle \csc(2\pi -\theta )=-\csc(\theta )=\csc(-\theta )} sec ( − θ ) = + sec θ {\displaystyle \sec(-\theta )=+\sec \theta } sec ( π 2 − θ ) = csc θ {\displaystyle \sec \left({\tfrac {\pi }{2}}-\theta \right)=\csc \theta } sec ( π − θ ) = − sec θ {\displaystyle \sec(\pi -\theta )=-\sec \theta } sec ( 3 π 2 − θ ) = − csc θ {\displaystyle \sec \left({\tfrac {3\pi }{2}}-\theta \right)=-\csc \theta } sec ( 2 π − θ ) = + sec ( θ ) = sec ( − θ ) {\displaystyle \sec(2\pi -\theta )=+\sec(\theta )=\sec(-\theta )} cot ( − θ ) = − cot θ {\displaystyle \cot(-\theta )=-\cot \theta } cot ( π 2 − θ ) = tan θ {\displaystyle \cot \left({\tfrac {\pi }{2}}-\theta \right)=\tan \theta } cot ( π − θ ) = − cot θ {\displaystyle \cot(\pi -\theta )=-\cot \theta } cot ( 3 π 2 − θ ) = + tan θ {\displaystyle \cot \left({\tfrac {3\pi }{2}}-\theta \right)=+\tan \theta } cot ( 2 π − θ ) = − cot ( θ ) = cot ( − θ ) {\displaystyle \cot(2\pi -\theta )=-\cot(\theta )=\cot(-\theta )}
Смены и периодичность Преобразование координат ( a , b ) при смещении угла с шагом θ {\displaystyle \theta } π 2 {\displaystyle {\frac {\pi }{2}}} Сдвиг на одну четверть периода Сдвиг на половину периода Сдвиг на полные периоды [4] Период sin ( θ ± π 2 ) = ± cos θ {\displaystyle \sin(\theta \pm {\tfrac {\pi }{2}})=\pm \cos \theta } sin ( θ + π ) = − sin θ {\displaystyle \sin(\theta +\pi )=-\sin \theta } sin ( θ + k ⋅ 2 π ) = + sin θ {\displaystyle \sin(\theta +k\cdot 2\pi )=+\sin \theta } 2 π {\displaystyle 2\pi } cos ( θ ± π 2 ) = ∓ sin θ {\displaystyle \cos(\theta \pm {\tfrac {\pi }{2}})=\mp \sin \theta } cos ( θ + π ) = − cos θ {\displaystyle \cos(\theta +\pi )=-\cos \theta } cos ( θ + k ⋅ 2 π ) = + cos θ {\displaystyle \cos(\theta +k\cdot 2\pi )=+\cos \theta } 2 π {\displaystyle 2\pi } csc ( θ ± π 2 ) = ± sec θ {\displaystyle \csc(\theta \pm {\tfrac {\pi }{2}})=\pm \sec \theta } csc ( θ + π ) = − csc θ {\displaystyle \csc(\theta +\pi )=-\csc \theta } csc ( θ + k ⋅ 2 π ) = + csc θ {\displaystyle \csc(\theta +k\cdot 2\pi )=+\csc \theta } 2 π {\displaystyle 2\pi } sec ( θ ± π 2 ) = ∓ csc θ {\displaystyle \sec(\theta \pm {\tfrac {\pi }{2}})=\mp \csc \theta } sec ( θ + π ) = − sec θ {\displaystyle \sec(\theta +\pi )=-\sec \theta } sec ( θ + k ⋅ 2 π ) = + sec θ {\displaystyle \sec(\theta +k\cdot 2\pi )=+\sec \theta } 2 π {\displaystyle 2\pi } tan ( θ ± π 4 ) = tan θ ± 1 1 ∓ tan θ {\displaystyle \tan(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\tan \theta \pm 1}{1\mp \tan \theta }}} tan ( θ + π 2 ) = − cot θ {\displaystyle \tan(\theta +{\tfrac {\pi }{2}})=-\cot \theta } tan ( θ + k ⋅ π ) = + tan θ {\displaystyle \tan(\theta +k\cdot \pi )=+\tan \theta } π {\displaystyle \pi } cot ( θ ± π 4 ) = cot θ ∓ 1 1 ± cot θ {\displaystyle \cot(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\cot \theta \mp 1}{1\pm \cot \theta }}} cot ( θ + π 2 ) = − tan θ {\displaystyle \cot(\theta +{\tfrac {\pi }{2}})=-\tan \theta } cot ( θ + k ⋅ π ) = + cot θ {\displaystyle \cot(\theta +k\cdot \pi )=+\cot \theta } π {\displaystyle \pi }
Знаки Знак тригонометрических функций зависит от квадранта угла. Если и sgn — знаковая функция , − π < θ ≤ π {\displaystyle {-\pi }<\theta \leq \pi }
sgn ( sin θ ) = sgn ( csc θ ) = { + 1 if 0 < θ < π − 1 if − π < θ < 0 0 if θ ∈ { 0 , π } sgn ( cos θ ) = sgn ( sec θ ) = { + 1 if − 1 2 π < θ < 1 2 π − 1 if − π < θ < − 1 2 π or 1 2 π < θ < π 0 if θ ∈ { − 1 2 π , 1 2 π } sgn ( tan θ ) = sgn ( cot θ ) = { + 1 if − π < θ < − 1 2 π or 0 < θ < 1 2 π − 1 if − 1 2 π < θ < 0 or 1 2 π < θ < π 0 if θ ∈ { − 1 2 π , 0 , 1 2 π , π } {\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}
Тригонометрические функции являются периодическими с общим периодом, поэтому для значений θ вне интервала они принимают повторяющиеся значения (см. § Сдвиги и периодичность выше). 2 π , {\displaystyle 2\pi ,} ( − π , π ] , {\displaystyle ({-\pi },\pi ],}
Тождества суммы и разности углов Иллюстрация формул сложения углов для синуса и косинуса острых углов. Выделенный отрезок имеет единичную длину. Диаграмма, показывающая тождества разности углов для и sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} cos ( α − β ) {\displaystyle \cos(\alpha -\beta )} Они также известны как теоремы (или формулы ) сложения и вычитания углов . sin ( α + β ) = sin α cos β + cos α sin β sin ( α − β ) = sin α cos β − cos α sin β cos ( α + β ) = cos α cos β − sin α sin β cos ( α − β ) = cos α cos β + sin α sin β {\displaystyle {\begin{aligned}\sin(\alpha +\beta )&=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\\sin(\alpha -\beta )&=\sin \alpha \cos \beta -\cos \alpha \sin \beta \\\cos(\alpha +\beta )&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\cos(\alpha -\beta )&=\cos \alpha \cos \beta +\sin \alpha \sin \beta \end{aligned}}}
Тождества разности углов для и могут быть выведены из версий суммы углов путем замены и использования фактов, что и . Их также можно вывести, используя слегка измененную версию рисунка для тождеств суммы углов, оба из которых показаны здесь. sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} cos ( α − β ) {\displaystyle \cos(\alpha -\beta )} − β {\displaystyle -\beta } β {\displaystyle \beta } sin ( − β ) = − sin ( β ) {\displaystyle \sin(-\beta )=-\sin(\beta )} cos ( − β ) = cos ( β ) {\displaystyle \cos(-\beta )=\cos(\beta )}
Эти тождества обобщены в первых двух строках следующей таблицы, которая также включает тождества сумм и разностей для других тригонометрических функций.
Синус sin ( α ± β ) {\displaystyle \sin(\alpha \pm \beta )} = {\displaystyle =} sin α cos β ± cos α sin β {\displaystyle \sin \alpha \cos \beta \pm \cos \alpha \sin \beta } [5] [6] Косинус cos ( α ± β ) {\displaystyle \cos(\alpha \pm \beta )} = {\displaystyle =} cos α cos β ∓ sin α sin β {\displaystyle \cos \alpha \cos \beta \mp \sin \alpha \sin \beta } [6] [7] Тангенс tan ( α ± β ) {\displaystyle \tan(\alpha \pm \beta )} = {\displaystyle =} tan α ± tan β 1 ∓ tan α tan β {\displaystyle {\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}} [6] [8] Косеканс csc ( α ± β ) {\displaystyle \csc(\alpha \pm \beta )} = {\displaystyle =} sec α sec β csc α csc β sec α csc β ± csc α sec β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\sec \alpha \csc \beta \pm \csc \alpha \sec \beta }}} [9] Секущая sec ( α ± β ) {\displaystyle \sec(\alpha \pm \beta )} = {\displaystyle =} sec α sec β csc α csc β csc α csc β ∓ sec α sec β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\csc \alpha \csc \beta \mp \sec \alpha \sec \beta }}} [9] Котангенс cot ( α ± β ) {\displaystyle \cot(\alpha \pm \beta )} = {\displaystyle =} cot α cot β ∓ 1 cot β ± cot α {\displaystyle {\frac {\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha }}} [6] [10] Арксинус arcsin x ± arcsin y {\displaystyle \arcsin x\pm \arcsin y} = {\displaystyle =} arcsin ( x 1 − y 2 ± y 1 − x 2 y ) {\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}\pm y{\sqrt {1-x^{2}{\vphantom {y}}}}\right)} [11] Арккосинус arccos x ± arccos y {\displaystyle \arccos x\pm \arccos y} = {\displaystyle =} arccos ( x y ∓ ( 1 − x 2 ) ( 1 − y 2 ) ) {\displaystyle \arccos \left(xy\mp {\sqrt {\left(1-x^{2}\right)\left(1-y^{2}\right)}}\right)} [12] Арктангенс arctan x ± arctan y {\displaystyle \arctan x\pm \arctan y} = {\displaystyle =} arctan ( x ± y 1 ∓ x y ) {\displaystyle \arctan \left({\frac {x\pm y}{1\mp xy}}\right)} [13] Арккотангенс arccot x ± arccot y {\displaystyle \operatorname {arccot} x\pm \operatorname {arccot} y} = {\displaystyle =} arccot ( x y ∓ 1 y ± x ) {\displaystyle \operatorname {arccot} \left({\frac {xy\mp 1}{y\pm x}}\right)}
Синусы и косинусы сумм бесконечного числа углов Когда ряд сходится абсолютно, то ∑ i = 1 ∞ θ i {\textstyle \sum _{i=1}^{\infty }\theta _{i}}
sin ( ∑ i = 1 ∞ θ i ) = ∑ odd k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ( ∏ i ∈ A sin θ i ∏ i ∉ A cos θ i ) cos ( ∑ i = 1 ∞ θ i ) = ∑ even k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ( ∏ i ∈ A sin θ i ∏ i ∉ A cos θ i ) . {\displaystyle {\begin{aligned}{\sin }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggl )}&=\sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\!\!\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}\\{\cos }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggr )}&=\sum _{{\text{even}}\ k\geq 0}(-1)^{\frac {k}{2}}\,\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}.\end{aligned}}}
Поскольку ряд сходится абсолютно, то обязательно имеет место и В частности, в этих двух тождествах появляется асимметрия, которая не наблюдается в случае сумм конечного числа углов: в каждом произведении имеется только конечное число синусных множителей, но имеется коконечное число косинусных множителей. Члены с бесконечным числом синусных множителей обязательно будут равны нулю. ∑ i = 1 ∞ θ i {\textstyle \sum _{i=1}^{\infty }\theta _{i}} lim i → ∞ θ i = 0 , {\textstyle \lim _{i\to \infty }\theta _{i}=0,} lim i → ∞ sin θ i = 0 , {\textstyle \lim _{i\to \infty }\sin \theta _{i}=0,} lim i → ∞ cos θ i = 1. {\textstyle \lim _{i\to \infty }\cos \theta _{i}=1.}
Когда только конечное число углов не равно нулю, то только конечное число членов в правой части не равно нулю, поскольку все, кроме конечного числа синусных множителей, равны нулю. Более того, в каждом члене все, кроме конечного числа косинусных множителей, равны единице. θ i {\displaystyle \theta _{i}}
Тангенсы и котангенсы сумм Пусть (для ) будет элементарным симметрическим многочленом степени k от переменных
для , то есть, e k {\displaystyle e_{k}} k = 0 , 1 , 2 , 3 , … {\displaystyle k=0,1,2,3,\ldots } x i = tan θ i {\displaystyle x_{i}=\tan \theta _{i}} i = 0 , 1 , 2 , 3 , … , {\displaystyle i=0,1,2,3,\ldots ,}
e 0 = 1 e 1 = ∑ i x i = ∑ i tan θ i e 2 = ∑ i < j x i x j = ∑ i < j tan θ i tan θ j e 3 = ∑ i < j < k x i x j x k = ∑ i < j < k tan θ i tan θ j tan θ k ⋮ ⋮ {\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{aligned}}}
Затем
tan ( ∑ i θ i ) = sin ( ∑ i θ i ) / ∏ i cos θ i cos ( ∑ i θ i ) / ∏ i cos θ i = ∑ odd k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ∏ i ∈ A tan θ i ∑ even k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ∏ i ∈ A tan θ i = e 1 − e 3 + e 5 − ⋯ e 0 − e 2 + e 4 − ⋯ cot ( ∑ i θ i ) = e 0 − e 2 + e 4 − ⋯ e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}{\tan }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {{\sin }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\[10pt]&={\frac {\displaystyle \sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\[10pt]{\cot }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
используя приведенные выше формулы суммы синуса и косинуса.
Количество членов в правой части зависит от количества членов в левой части.
Например: tan ( θ 1 + θ 2 ) = e 1 e 0 − e 2 = x 1 + x 2 1 − x 1 x 2 = tan θ 1 + tan θ 2 1 − tan θ 1 tan θ 2 , tan ( θ 1 + θ 2 + θ 3 ) = e 1 − e 3 e 0 − e 2 = ( x 1 + x 2 + x 3 ) − ( x 1 x 2 x 3 ) 1 − ( x 1 x 2 + x 1 x 3 + x 2 x 3 ) , tan ( θ 1 + θ 2 + θ 3 + θ 4 ) = e 1 − e 3 e 0 − e 2 + e 4 = ( x 1 + x 2 + x 3 + x 4 ) − ( x 1 x 2 x 3 + x 1 x 2 x 4 + x 1 x 3 x 4 + x 2 x 3 x 4 ) 1 − ( x 1 x 2 + x 1 x 3 + x 1 x 4 + x 2 x 3 + x 2 x 4 + x 3 x 4 ) + ( x 1 x 2 x 3 x 4 ) , {\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}
и так далее. Случай только конечного числа членов может быть доказан с помощью математической индукции . [14] Случай бесконечного числа членов может быть доказан с помощью некоторых элементарных неравенств. [15]
Секансы и косекансы сумм sec ( ∑ i θ i ) = ∏ i sec θ i e 0 − e 2 + e 4 − ⋯ csc ( ∑ i θ i ) = ∏ i sec θ i e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}{\sec }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\[8pt]{\csc }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
где — элементарный симметрический многочлен степени k от n переменных , а число членов в знаменателе и число множителей в произведении в числителе зависят от числа членов в сумме слева. [16] Случай только конечного числа членов может быть доказан методом математической индукции по числу таких членов. e k {\displaystyle e_{k}} x i = tan θ i , {\displaystyle x_{i}=\tan \theta _{i},} i = 1 , … , n , {\displaystyle i=1,\ldots ,n,}
Например,
sec ( α + β + γ ) = sec α sec β sec γ 1 − tan α tan β − tan α tan γ − tan β tan γ csc ( α + β + γ ) = sec α sec β sec γ tan α + tan β + tan γ − tan α tan β tan γ . {\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}
Диаграмма, иллюстрирующая связь между теоремой Птолемея и тригонометрическим тождеством суммы углов для синуса. Теорема Птолемея утверждает, что сумма произведений длин противоположных сторон равна произведению длин диагоналей. Когда эти длины сторон выражаются через значения sin и cos, показанные на рисунке выше, это дает тригонометрическое тождество суммы углов для синуса: sin( α + β ) = sin α cos β + cos α sin β . Теорема Птолемея важна в истории тригонометрических тождеств, поскольку именно так были впервые доказаны результаты, эквивалентные формулам суммы и разности для синуса и косинуса. Она утверждает, что во вписанном четырехугольнике , как показано на прилагаемом рисунке, сумма произведений длин противоположных сторон равна произведению длин диагоналей. В особых случаях, когда одна из диагоналей или сторон является диаметром окружности, эта теорема приводит непосредственно к тригонометрическим тождествам суммы и разности углов. [17] Соотношение следует проще всего, когда окружность построена так, чтобы иметь диаметр длины один, как показано здесь. A B C D {\displaystyle ABCD}
По теореме Фалеса , и оба являются прямыми углами. Прямоугольные треугольники и оба имеют общую гипотенузу длины 1. Таким образом, сторона , , и . ∠ D A B {\displaystyle \angle DAB} ∠ D C B {\displaystyle \angle DCB} D A B {\displaystyle DAB} D C B {\displaystyle DCB} B D ¯ {\displaystyle {\overline {BD}}} A B ¯ = sin α {\displaystyle {\overline {AB}}=\sin \alpha } A D ¯ = cos α {\displaystyle {\overline {AD}}=\cos \alpha } B C ¯ = sin β {\displaystyle {\overline {BC}}=\sin \beta } C D ¯ = cos β {\displaystyle {\overline {CD}}=\cos \beta }
По теореме о вписанном угле центральный угол, опирающийся на хорду в центре окружности, в два раза больше угла , то есть . Следовательно, симметричная пара красных треугольников имеет угол в центре. Каждый из этих треугольников имеет гипотенузу длиной , поэтому длина равна , то есть просто . Другая диагональ четырехугольника является диаметром длиной 1, поэтому произведение длин диагоналей также равно . A C ¯ {\displaystyle {\overline {AC}}} ∠ A D C {\displaystyle \angle ADC} 2 ( α + β ) {\displaystyle 2(\alpha +\beta )} α + β {\displaystyle \alpha +\beta } 1 2 {\textstyle {\frac {1}{2}}} A C ¯ {\displaystyle {\overline {AC}}} 2 × 1 2 sin ( α + β ) {\textstyle 2\times {\frac {1}{2}}\sin(\alpha +\beta )} sin ( α + β ) {\displaystyle \sin(\alpha +\beta )} sin ( α + β ) {\displaystyle \sin(\alpha +\beta )}
Когда эти значения подставляются в утверждение теоремы Птолемея, что , это дает тригонометрическое тождество суммы углов для синуса: . Формула разности углов для может быть получена аналогичным образом, если вместо брать сторону в качестве диаметра . [17] | A C ¯ | ⋅ | B D ¯ | = | A B ¯ | ⋅ | C D ¯ | + | A D ¯ | ⋅ | B C ¯ | {\displaystyle |{\overline {AC}}|\cdot |{\overline {BD}}|=|{\overline {AB}}|\cdot |{\overline {CD}}|+|{\overline {AD}}|\cdot |{\overline {BC}}|} sin ( α + β ) = sin α cos β + cos α sin β {\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta } sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} C D ¯ {\displaystyle {\overline {CD}}} B D ¯ {\displaystyle {\overline {BD}}}
T n — n -й полином Чебышева cos ( n θ ) = T n ( cos θ ) {\displaystyle \cos(n\theta )=T_{n}(\cos \theta )} [18] Формула де Муавра , i — мнимая единица cos ( n θ ) + i sin ( n θ ) = ( cos θ + i sin θ ) n {\displaystyle \cos(n\theta )+i\sin(n\theta )=(\cos \theta +i\sin \theta )^{n}} [19]
Визуальная демонстрация формулы двойного угла для синуса. Для приведенного выше равнобедренного треугольника с единичными сторонами и углом площадь 2 θ {\displaystyle 2\theta } 1 / 2 sin θ cos θ {\displaystyle \sin \theta \cos \theta } 1 2 sin 2 θ {\textstyle {\frac {1}{2}}\sin 2\theta } sin 2 θ = 2 sin θ cos θ . {\displaystyle \sin 2\theta =2\sin \theta \cos \theta .} Формулы для удвоенного угла. [20]
sin ( 2 θ ) = 2 sin θ cos θ = ( sin θ + cos θ ) 2 − 1 = 2 tan θ 1 + tan 2 θ {\displaystyle \sin(2\theta )=2\sin \theta \cos \theta =(\sin \theta +\cos \theta )^{2}-1={\frac {2\tan \theta }{1+\tan ^{2}\theta }}} cos ( 2 θ ) = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ = 1 − tan 2 θ 1 + tan 2 θ {\displaystyle \cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta =2\cos ^{2}\theta -1=1-2\sin ^{2}\theta ={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}} tan ( 2 θ ) = 2 tan θ 1 − tan 2 θ {\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}} cot ( 2 θ ) = cot 2 θ − 1 2 cot θ = 1 − tan 2 θ 2 tan θ {\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {1-\tan ^{2}\theta }{2\tan \theta }}} sec ( 2 θ ) = sec 2 θ 2 − sec 2 θ = 1 + tan 2 θ 1 − tan 2 θ {\displaystyle \sec(2\theta )={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }}={\frac {1+\tan ^{2}\theta }{1-\tan ^{2}\theta }}} csc ( 2 θ ) = sec θ csc θ 2 = 1 + tan 2 θ 2 tan θ {\displaystyle \csc(2\theta )={\frac {\sec \theta \csc \theta }{2}}={\frac {1+\tan ^{2}\theta }{2\tan \theta }}}
Формулы для тройных углов. [20]
sin ( 3 θ ) = 3 sin θ − 4 sin 3 θ = 4 sin θ sin ( π 3 − θ ) sin ( π 3 + θ ) {\displaystyle \sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin \left({\frac {\pi }{3}}-\theta \right)\sin \left({\frac {\pi }{3}}+\theta \right)} cos ( 3 θ ) = 4 cos 3 θ − 3 cos θ = 4 cos θ cos ( π 3 − θ ) cos ( π 3 + θ ) {\displaystyle \cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \cos \left({\frac {\pi }{3}}-\theta \right)\cos \left({\frac {\pi }{3}}+\theta \right)} tan ( 3 θ ) = 3 tan θ − tan 3 θ 1 − 3 tan 2 θ = tan θ tan ( π 3 − θ ) tan ( π 3 + θ ) {\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan \left({\frac {\pi }{3}}-\theta \right)\tan \left({\frac {\pi }{3}}+\theta \right)} cot ( 3 θ ) = 3 cot θ − cot 3 θ 1 − 3 cot 2 θ {\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}} sec ( 3 θ ) = sec 3 θ 4 − 3 sec 2 θ {\displaystyle \sec(3\theta )={\frac {\sec ^{3}\theta }{4-3\sec ^{2}\theta }}} csc ( 3 θ ) = csc 3 θ 3 csc 2 θ − 4 {\displaystyle \csc(3\theta )={\frac {\csc ^{3}\theta }{3\csc ^{2}\theta -4}}}
Формулы для нескольких углов. [21]
sin ( n θ ) = ∑ k odd ( − 1 ) k − 1 2 ( n k ) cos n − k θ sin k θ = sin θ ∑ i = 0 ( n + 1 ) / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i + 1 ) ( i j ) cos n − 2 ( i − j ) − 1 θ = sin ( θ ) ⋅ ∑ k = 0 ⌊ n − 1 2 ⌋ ( − 1 ) k ⋅ ( 2 ⋅ cos ( θ ) ) n − 2 k − 1 ⋅ ( n − k − 1 k ) = 2 ( n − 1 ) ∏ k = 0 n − 1 sin ( k π / n + θ ) {\displaystyle {\begin{aligned}\sin(n\theta )&=\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sin \theta \sum _{i=0}^{(n+1)/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i+1}{i \choose j}\cos ^{n-2(i-j)-1}\theta \\{}&=\sin(\theta )\cdot \sum _{k=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }(-1)^{k}\cdot {(2\cdot \cos(\theta ))}^{n-2k-1}\cdot {n-k-1 \choose k}\\{}&=2^{(n-1)}\prod _{k=0}^{n-1}\sin(k\pi /n+\theta )\end{aligned}}} cos ( n θ ) = ∑ k even ( − 1 ) k 2 ( n k ) cos n − k θ sin k θ = ∑ i = 0 n / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i ) ( i j ) cos n − 2 ( i − j ) θ = ∑ k = 0 ⌊ n 2 ⌋ ( − 1 ) k ⋅ ( 2 ⋅ cos ( θ ) ) n − 2 k ⋅ ( n − k k ) ⋅ n 2 n − 2 k {\displaystyle {\begin{aligned}\cos(n\theta )&=\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sum _{i=0}^{n/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i}{i \choose j}\cos ^{n-2(i-j)}\theta \\{}&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{k}\cdot {(2\cdot \cos(\theta ))}^{n-2k}\cdot {n-k \choose k}\cdot {\frac {n}{2n-2k}}\end{aligned}}} cos ( ( 2 n + 1 ) θ ) = ( − 1 ) n 2 2 n ∏ k = 0 2 n cos ( k π / ( 2 n + 1 ) − θ ) {\displaystyle \cos((2n+1)\theta )=(-1)^{n}2^{2n}\prod _{k=0}^{2n}\cos(k\pi /(2n+1)-\theta )} cos ( 2 n θ ) = ( − 1 ) n 2 2 n − 1 ∏ k = 0 2 n − 1 cos ( ( 1 + 2 k ) π / ( 4 n ) − θ ) {\displaystyle \cos(2n\theta )=(-1)^{n}2^{2n-1}\prod _{k=0}^{2n-1}\cos((1+2k)\pi /(4n)-\theta )} tan ( n θ ) = ∑ k odd ( − 1 ) k − 1 2 ( n k ) tan k θ ∑ k even ( − 1 ) k 2 ( n k ) tan k θ {\displaystyle \tan(n\theta )={\frac {\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\tan ^{k}\theta }{\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\tan ^{k}\theta }}}
метод Чебышева Метод Чебышева представляет собой рекурсивный алгоритм для нахождения формулы n- го кратного угла, зная значения th и th. [22] ( n − 1 ) {\displaystyle (n-1)} ( n − 2 ) {\displaystyle (n-2)}
cos ( n x ) {\displaystyle \cos(nx)} cos ( ( n − 1 ) x ) {\displaystyle \cos((n-1)x)} cos ( ( n − 2 ) x ) {\displaystyle \cos((n-2)x)} cos ( x ) {\displaystyle \cos(x)}
cos ( n x ) = 2 cos x cos ( ( n − 1 ) x ) − cos ( ( n − 2 ) x ) . {\displaystyle \cos(nx)=2\cos x\cos((n-1)x)-\cos((n-2)x).}
Это можно доказать, сложив формулы
cos ( ( n − 1 ) x + x ) = cos ( ( n − 1 ) x ) cos x − sin ( ( n − 1 ) x ) sin x cos ( ( n − 1 ) x − x ) = cos ( ( n − 1 ) x ) cos x + sin ( ( n − 1 ) x ) sin x {\displaystyle {\begin{aligned}\cos((n-1)x+x)&=\cos((n-1)x)\cos x-\sin((n-1)x)\sin x\\\cos((n-1)x-x)&=\cos((n-1)x)\cos x+\sin((n-1)x)\sin x\end{aligned}}}
По индукции следует, что является многочленом так называемого многочлена Чебышёва первого рода, см. Многочлены Чебышёва#Тригонометрическое определение . cos ( n x ) {\displaystyle \cos(nx)} cos x , {\displaystyle \cos x,}
Аналогично, можно вычислить из и с помощью
Это можно доказать, добавив формулы для и sin ( n x ) {\displaystyle \sin(nx)} sin ( ( n − 1 ) x ) , {\displaystyle \sin((n-1)x),} sin ( ( n − 2 ) x ) , {\displaystyle \sin((n-2)x),} cos x {\displaystyle \cos x} sin ( n x ) = 2 cos x sin ( ( n − 1 ) x ) − sin ( ( n − 2 ) x ) {\displaystyle \sin(nx)=2\cos x\sin((n-1)x)-\sin((n-2)x)} sin ( ( n − 1 ) x + x ) {\displaystyle \sin((n-1)x+x)} sin ( ( n − 1 ) x − x ) . {\displaystyle \sin((n-1)x-x).}
Служа целям, аналогичным целям метода Чебышева, для касательной можно записать:
tan ( n x ) = tan ( ( n − 1 ) x ) + tan x 1 − tan ( ( n − 1 ) x ) tan x . {\displaystyle \tan(nx)={\frac {\tan((n-1)x)+\tan x}{1-\tan((n-1)x)\tan x}}\,.}
sin θ 2 = sgn ( sin θ 2 ) 1 − cos θ 2 cos θ 2 = sgn ( cos θ 2 ) 1 + cos θ 2 tan θ 2 = 1 − cos θ sin θ = sin θ 1 + cos θ = csc θ − cot θ = tan θ 1 + sec θ = sgn ( sin θ ) 1 − cos θ 1 + cos θ = − 1 + sgn ( cos θ ) 1 + tan 2 θ tan θ cot θ 2 = 1 + cos θ sin θ = sin θ 1 − cos θ = csc θ + cot θ = sgn ( sin θ ) 1 + cos θ 1 − cos θ sec θ 2 = sgn ( cos θ 2 ) 2 1 + cos θ csc θ 2 = sgn ( sin θ 2 ) 2 1 − cos θ {\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\[3pt]\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\[3pt]\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\[6mu]&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\[3pt]\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}} [23] [24]
Также tan η ± θ 2 = sin η ± sin θ cos η + cos θ tan ( θ 2 + π 4 ) = sec θ + tan θ 1 − sin θ 1 + sin θ = | 1 − tan θ 2 | | 1 + tan θ 2 | {\displaystyle {\begin{aligned}\tan {\frac {\eta \pm \theta }{2}}&={\frac {\sin \eta \pm \sin \theta }{\cos \eta +\cos \theta }}\\[3pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[3pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\end{aligned}}}
Стол Их можно показать, используя либо тождества суммы и разности, либо формулы множественных углов.
Синус Косинус Тангенс Котангенс Формула двойного угла [25] [26] sin ( 2 θ ) = 2 sin θ cos θ = 2 tan θ 1 + tan 2 θ {\displaystyle {\begin{aligned}\sin(2\theta )&=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}} cos ( 2 θ ) = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ = 1 − tan 2 θ 1 + tan 2 θ {\displaystyle {\begin{aligned}\cos(2\theta )&=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}} tan ( 2 θ ) = 2 tan θ 1 − tan 2 θ {\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}} cot ( 2 θ ) = cot 2 θ − 1 2 cot θ {\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}} Формула тройного угла [18] [27] sin ( 3 θ ) = − sin 3 θ + 3 cos 2 θ sin θ = − 4 sin 3 θ + 3 sin θ {\displaystyle {\begin{aligned}\sin(3\theta )&=-\sin ^{3}\theta +3\cos ^{2}\theta \sin \theta \\&=-4\sin ^{3}\theta +3\sin \theta \end{aligned}}} cos ( 3 θ ) = cos 3 θ − 3 sin 2 θ cos θ = 4 cos 3 θ − 3 cos θ {\displaystyle {\begin{aligned}\cos(3\theta )&=\cos ^{3}\theta -3\sin ^{2}\theta \cos \theta \\&=4\cos ^{3}\theta -3\cos \theta \end{aligned}}} tan ( 3 θ ) = 3 tan θ − tan 3 θ 1 − 3 tan 2 θ {\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}} cot ( 3 θ ) = 3 cot θ − cot 3 θ 1 − 3 cot 2 θ {\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}} Формула половинного угла [23] [24] sin θ 2 = sgn ( sin θ 2 ) 1 − cos θ 2 ( or sin 2 θ 2 = 1 − cos θ 2 ) {\displaystyle {\begin{aligned}&\sin {\frac {\theta }{2}}=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\\\&\left({\text{or }}\sin ^{2}{\frac {\theta }{2}}={\frac {1-\cos \theta }{2}}\right)\end{aligned}}} cos θ 2 = sgn ( cos θ 2 ) 1 + cos θ 2 ( or cos 2 θ 2 = 1 + cos θ 2 ) {\displaystyle {\begin{aligned}&\cos {\frac {\theta }{2}}=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\\\&\left({\text{or }}\cos ^{2}{\frac {\theta }{2}}={\frac {1+\cos \theta }{2}}\right)\end{aligned}}} tan θ 2 = csc θ − cot θ = ± 1 − cos θ 1 + cos θ = sin θ 1 + cos θ = 1 − cos θ sin θ tan η + θ 2 = sin η + sin θ cos η + cos θ tan ( θ 2 + π 4 ) = sec θ + tan θ 1 − sin θ 1 + sin θ = | 1 − tan θ 2 | | 1 + tan θ 2 | tan θ 2 = tan θ 1 + 1 + tan 2 θ for θ ∈ ( − π 2 , π 2 ) {\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1+\cos \theta }}\\[3pt]&={\frac {1-\cos \theta }{\sin \theta }}\\[5pt]\tan {\frac {\eta +\theta }{2}}&={\frac {\sin \eta +\sin \theta }{\cos \eta +\cos \theta }}\\[5pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[5pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\\[5pt]\tan {\frac {\theta }{2}}&={\frac {\tan \theta }{1+{\sqrt {1+\tan ^{2}\theta }}}}\\&{\text{for }}\theta \in \left(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right)\end{aligned}}} cot θ 2 = csc θ + cot θ = ± 1 + cos θ 1 − cos θ = sin θ 1 − cos θ = 1 + cos θ sin θ {\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1-\cos \theta }}\\[4pt]&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}}
Тот факт, что формула тройного угла для синуса и косинуса содержит только степени одной функции, позволяет связать геометрическую задачу построения трисекции угла с помощью циркуля и линейки с алгебраической задачей решения кубического уравнения , что позволяет доказать, что трисекция в общем случае невозможна с использованием данных инструментов.
Формула для вычисления тригонометрических тождеств для угла в одну треть существует, но она требует нахождения нулей кубического уравнения 4 x 3 − 3 x + d = 0 , где — значение косинуса при угле в одну треть, а d — известное значение косинуса при полном угле. Однако дискриминант этого уравнения положителен, поэтому это уравнение имеет три действительных корня (из которых только один является решением для косинуса угла в одну треть). Ни одно из этих решений не сводится к действительному алгебраическому выражению , поскольку они используют промежуточные комплексные числа под кубическими корнями . x {\displaystyle x}
Получено путем решения второй и третьей версии формулы косинуса двойного угла.
Синус Косинус Другой sin 2 θ = 1 − cos ( 2 θ ) 2 {\displaystyle \sin ^{2}\theta ={\frac {1-\cos(2\theta )}{2}}} cos 2 θ = 1 + cos ( 2 θ ) 2 {\displaystyle \cos ^{2}\theta ={\frac {1+\cos(2\theta )}{2}}} sin 2 θ cos 2 θ = 1 − cos ( 4 θ ) 8 {\displaystyle \sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos(4\theta )}{8}}} sin 3 θ = 3 sin θ − sin ( 3 θ ) 4 {\displaystyle \sin ^{3}\theta ={\frac {3\sin \theta -\sin(3\theta )}{4}}} cos 3 θ = 3 cos θ + cos ( 3 θ ) 4 {\displaystyle \cos ^{3}\theta ={\frac {3\cos \theta +\cos(3\theta )}{4}}} sin 3 θ cos 3 θ = 3 sin ( 2 θ ) − sin ( 6 θ ) 32 {\displaystyle \sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin(2\theta )-\sin(6\theta )}{32}}} sin 4 θ = 3 − 4 cos ( 2 θ ) + cos ( 4 θ ) 8 {\displaystyle \sin ^{4}\theta ={\frac {3-4\cos(2\theta )+\cos(4\theta )}{8}}} cos 4 θ = 3 + 4 cos ( 2 θ ) + cos ( 4 θ ) 8 {\displaystyle \cos ^{4}\theta ={\frac {3+4\cos(2\theta )+\cos(4\theta )}{8}}} sin 4 θ cos 4 θ = 3 − 4 cos ( 4 θ ) + cos ( 8 θ ) 128 {\displaystyle \sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos(4\theta )+\cos(8\theta )}{128}}} sin 5 θ = 10 sin θ − 5 sin ( 3 θ ) + sin ( 5 θ ) 16 {\displaystyle \sin ^{5}\theta ={\frac {10\sin \theta -5\sin(3\theta )+\sin(5\theta )}{16}}} cos 5 θ = 10 cos θ + 5 cos ( 3 θ ) + cos ( 5 θ ) 16 {\displaystyle \cos ^{5}\theta ={\frac {10\cos \theta +5\cos(3\theta )+\cos(5\theta )}{16}}} sin 5 θ cos 5 θ = 10 sin ( 2 θ ) − 5 sin ( 6 θ ) + sin ( 10 θ ) 512 {\displaystyle \sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin(2\theta )-5\sin(6\theta )+\sin(10\theta )}{512}}}
Формула приведения косинуса к степени: наглядная диаграмма. Красный, оранжевый и синий треугольники подобны, а красный и оранжевый треугольники конгруэнтны. Гипотенуза синего треугольника имеет длину . Угол равен , поэтому основание этого треугольника имеет длину . Эта длина также равна сумме длин и , то есть . Следовательно, . Разделив обе стороны на, получаем формулу приведения косинуса к степени: . Формулу половинного угла для косинуса можно получить, заменив на и извлекая квадратный корень из обеих сторон: A D ¯ {\displaystyle {\overline {AD}}} 2 cos θ {\displaystyle 2\cos \theta } ∠ D A E {\displaystyle \angle DAE} θ {\displaystyle \theta } A E ¯ {\displaystyle {\overline {AE}}} 2 cos 2 θ {\displaystyle 2\cos ^{2}\theta } B D ¯ {\displaystyle {\overline {BD}}} A F ¯ {\displaystyle {\overline {AF}}} 1 + cos ( 2 θ ) {\displaystyle 1+\cos(2\theta )} 2 cos 2 θ = 1 + cos ( 2 θ ) {\displaystyle 2\cos ^{2}\theta =1+\cos(2\theta )} 2 {\displaystyle 2} cos 2 θ = {\displaystyle \cos ^{2}\theta =} 1 2 ( 1 + cos ( 2 θ ) ) {\textstyle {\frac {1}{2}}(1+\cos(2\theta ))} θ {\displaystyle \theta } θ / 2 {\displaystyle \theta /2} cos ( θ / 2 ) = ± ( 1 + cos θ ) / 2 . {\textstyle \cos \left(\theta /2\right)=\pm {\sqrt {\left(1+\cos \theta \right)/2}}.} Формула понижения степени синуса: наглядная диаграмма. Заштрихованные синий и зеленый треугольники, а также треугольник с красной рамкой — все прямоугольные и подобны, и все содержат угол . Гипотенуза треугольника с красной рамкой имеет длину , поэтому его сторона имеет длину . Отрезок прямой имеет длину и сумму длин и равен длине , которая равна 1. Следовательно, . Вычитание из обеих сторон и деление на 2 на два дает формулу понижения степени для синуса: . Формулу половинного угла для синуса можно получить, заменив на и извлекая квадратный корень из обеих сторон: Обратите внимание, что этот рисунок также иллюстрирует в вертикальном отрезке прямой , что . E B D {\displaystyle EBD} θ {\displaystyle \theta } B D ¯ {\displaystyle {\overline {BD}}} 2 sin θ {\displaystyle 2\sin \theta } D E ¯ {\displaystyle {\overline {DE}}} 2 sin 2 θ {\displaystyle 2\sin ^{2}\theta } A E ¯ {\displaystyle {\overline {AE}}} cos 2 θ {\displaystyle \cos 2\theta } A E ¯ {\displaystyle {\overline {AE}}} D E ¯ {\displaystyle {\overline {DE}}} A D ¯ {\displaystyle {\overline {AD}}} cos 2 θ + 2 sin 2 θ = 1 {\displaystyle \cos 2\theta +2\sin ^{2}\theta =1} cos 2 θ {\displaystyle \cos 2\theta } sin 2 θ = {\displaystyle \sin ^{2}\theta =} 1 2 ( 1 − cos ( 2 θ ) ) {\textstyle {\frac {1}{2}}(1-\cos(2\theta ))} θ {\displaystyle \theta } θ / 2 {\displaystyle \theta /2} sin ( θ / 2 ) = ± ( 1 − cos θ ) / 2 . {\textstyle \sin \left(\theta /2\right)=\pm {\sqrt {\left(1-\cos \theta \right)/2}}.} E B ¯ {\displaystyle {\overline {EB}}} sin 2 θ = 2 sin θ cos θ {\displaystyle \sin 2\theta =2\sin \theta \cos \theta }
В общих чертах для степеней или справедливо следующее утверждение, которое можно вывести с помощью формулы Муавра , формулы Эйлера и биномиальной теоремы . sin θ {\displaystyle \sin \theta } cos θ {\displaystyle \cos \theta }
если н это ... cos n θ {\displaystyle \cos ^{n}\theta } sin n θ {\displaystyle \sin ^{n}\theta } n нечетное cos n θ = 2 2 n ∑ k = 0 n − 1 2 ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}} sin n θ = 2 2 n ∑ k = 0 n − 1 2 ( − 1 ) ( n − 1 2 − k ) ( n k ) sin ( ( n − 2 k ) θ ) {\displaystyle \sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left({\frac {n-1}{2}}-k\right)}{\binom {n}{k}}\sin {{\big (}(n-2k)\theta {\big )}}} n четное cos n θ = 1 2 n ( n n 2 ) + 2 2 n ∑ k = 0 n 2 − 1 ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}} sin n θ = 1 2 n ( n n 2 ) + 2 2 n ∑ k = 0 n 2 − 1 ( − 1 ) ( n 2 − k ) ( n k ) cos ( ( n − 2 k ) θ ) {\displaystyle \sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{\left({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}
Тождества «произведение-сумма» и «сумма-произведение» Доказательство тождества суммы и разности к произведению косинуса для расчетов простефаэрезис с использованием равнобедренного треугольника Тождества произведения в сумму [28] или формулы простеаферезиса можно доказать, разложив их правые части с помощью теорем сложения углов. Исторически первые четыре из них были известны как формулы Вернера , в честь Иоганнеса Вернера , который использовал их для астрономических расчетов. [29] См. амплитудную модуляцию для применения формул произведения в сумму и биение (акустика) и фазовый детектор для применения формул суммы в произведение.
Идентификации произведения в сумму cos θ cos φ = 1 2 ( cos ( θ − φ ) + cos ( θ + φ ) ) sin θ sin φ = 1 2 ( cos ( θ − φ ) − cos ( θ + φ ) ) sin θ cos φ = 1 2 ( sin ( θ + φ ) + sin ( θ − φ ) ) cos θ sin φ = 1 2 ( sin ( θ + φ ) − sin ( θ − φ ) ) {\displaystyle {\begin{aligned}\cos \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )+\cos(\theta +\varphi ){\bigr )}\\[3mu]\sin \theta \,\sin \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )-\cos(\theta +\varphi ){\bigr )}\\[3mu]\sin \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )+\sin(\theta -\varphi ){\bigr )}\\[3mu]\cos \theta \,\sin \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )-\sin(\theta -\varphi ){\bigr )}\end{aligned}}} tan θ tan φ = cos ( θ − φ ) − cos ( θ + φ ) cos ( θ − φ ) + cos ( θ + φ ) {\displaystyle \tan \theta \,\tan \varphi ={\frac {\cos(\theta -\varphi )-\cos(\theta +\varphi )}{\cos(\theta -\varphi )+\cos(\theta +\varphi )}}} tan θ cot φ = sin ( θ + φ ) + sin ( θ − φ ) sin ( θ + φ ) − sin ( θ − φ ) {\displaystyle \tan \theta \,\cot \varphi ={\frac {\sin(\theta +\varphi )+\sin(\theta -\varphi )}{\sin(\theta +\varphi )-\sin(\theta -\varphi )}}} ∏ k = 1 n cos θ k = 1 2 n ∑ e ∈ S cos ( e 1 θ 1 + ⋯ + e n θ n ) where e = ( e 1 , … , e n ) ∈ S = { 1 , − 1 } n {\displaystyle {\begin{aligned}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\\[6pt]&{\text{where }}e=(e_{1},\ldots ,e_{n})\in S=\{1,-1\}^{n}\end{aligned}}} ∏ k = 1 n sin θ k = ( − 1 ) ⌊ n 2 ⌋ 2 n { ∑ e ∈ S cos ( e 1 θ 1 + ⋯ + e n θ n ) ∏ j = 1 n e j if n is even , ∑ e ∈ S sin ( e 1 θ 1 + ⋯ + e n θ n ) ∏ j = 1 n e j if n is odd {\displaystyle \prod _{k=1}^{n}\sin \theta _{k}={\frac {(-1)^{\left\lfloor {\frac {n}{2}}\right\rfloor }}{2^{n}}}{\begin{cases}\displaystyle \sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is even}},\\\displaystyle \sum _{e\in S}\sin(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is odd}}\end{cases}}}
Идентификации суммы и произведения Диаграмма, иллюстрирующая тождества суммы-произведения для синуса и косинуса. Синий прямоугольный треугольник имеет угол , а красный прямоугольный треугольник имеет угол . Оба имеют гипотенузу длины 1. Вспомогательные углы, здесь называемые и , построены таким образом, что и . Следовательно, и . Это позволяет построить два конгруэнтных треугольника с фиолетовым контуром и , каждый с гипотенузой и углом в основании. Сумма высот красного и синего треугольников равна , и это равно удвоенной высоте одного фиолетового треугольника, то есть . Запись и в этом уравнении через и дает тождество суммы-произведения для синуса: . Аналогично, сумма ширин красного и синего треугольников дает соответствующее тождество для косинуса. θ {\displaystyle \theta } φ {\displaystyle \varphi } p {\displaystyle p} q {\displaystyle q} p = ( θ + φ ) / 2 {\displaystyle p=(\theta +\varphi )/2} q = ( θ − φ ) / 2 {\displaystyle q=(\theta -\varphi )/2} θ = p + q {\displaystyle \theta =p+q} φ = p − q {\displaystyle \varphi =p-q} A F G {\displaystyle AFG} F C E {\displaystyle FCE} cos q {\displaystyle \cos q} p {\displaystyle p} sin θ + sin φ {\displaystyle \sin \theta +\sin \varphi } 2 sin p cos q {\displaystyle 2\sin p\cos q} p {\displaystyle p} q {\displaystyle q} θ {\displaystyle \theta } φ {\displaystyle \varphi } sin θ + sin φ = 2 sin ( θ + φ 2 ) cos ( θ − φ 2 ) {\displaystyle \sin \theta +\sin \varphi =2\sin \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)} Тождества суммы и произведения следующие: [30]
sin θ ± sin φ = 2 sin ( θ ± φ 2 ) cos ( θ ∓ φ 2 ) {\displaystyle \sin \theta \pm \sin \varphi =2\sin \left({\frac {\theta \pm \varphi }{2}}\right)\cos \left({\frac {\theta \mp \varphi }{2}}\right)} cos θ + cos φ = 2 cos ( θ + φ 2 ) cos ( θ − φ 2 ) {\displaystyle \cos \theta +\cos \varphi =2\cos \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)} cos θ − cos φ = − 2 sin ( θ + φ 2 ) sin ( θ − φ 2 ) {\displaystyle \cos \theta -\cos \varphi =-2\sin \left({\frac {\theta +\varphi }{2}}\right)\sin \left({\frac {\theta -\varphi }{2}}\right)} tan θ ± tan φ = sin ( θ ± φ ) cos θ cos φ {\displaystyle \tan \theta \pm \tan \varphi ={\frac {\sin(\theta \pm \varphi )}{\cos \theta \,\cos \varphi }}}
Чарльз Эрмит продемонстрировал следующее тождество. [31] Предположим, что являются комплексными числами , никакие два из которых не отличаются на целое число, кратное π . Пусть a 1 , … , a n {\displaystyle a_{1},\ldots ,a_{n}}
A n , k = ∏ 1 ≤ j ≤ n j ≠ k cot ( a k − a j ) {\displaystyle A_{n,k}=\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq k\end{smallmatrix}}\cot(a_{k}-a_{j})}
(в частности, будучи пустым произведением , равно 1). Тогда A 1 , 1 , {\displaystyle A_{1,1},}
cot ( z − a 1 ) ⋯ cot ( z − a n ) = cos n π 2 + ∑ k = 1 n A n , k cot ( z − a k ) . {\displaystyle \cot(z-a_{1})\cdots \cot(z-a_{n})=\cos {\frac {n\pi }{2}}+\sum _{k=1}^{n}A_{n,k}\cot(z-a_{k}).}
Простейшим нетривиальным примером является случай n = 2
cot ( z − a 1 ) cot ( z − a 2 ) = − 1 + cot ( a 1 − a 2 ) cot ( z − a 1 ) + cot ( a 2 − a 1 ) cot ( z − a 2 ) . {\displaystyle \cot(z-a_{1})\cot(z-a_{2})=-1+\cot(a_{1}-a_{2})\cot(z-a_{1})+\cot(a_{2}-a_{1})\cot(z-a_{2}).}
Конечные произведения тригонометрических функций Для взаимно простых целых чисел n , m
∏ k = 1 n ( 2 a + 2 cos ( 2 π k m n + x ) ) = 2 ( T n ( a ) + ( − 1 ) n + m cos ( n x ) ) {\displaystyle \prod _{k=1}^{n}\left(2a+2\cos \left({\frac {2\pi km}{n}}+x\right)\right)=2\left(T_{n}(a)+{(-1)}^{n+m}\cos(nx)\right)}
где T n — полином Чебышева . [ требуется ссылка
Для синусоидальной функции справедливо следующее соотношение:
∏ k = 1 n − 1 sin ( k π n ) = n 2 n − 1 . {\displaystyle \prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{n}}\right)={\frac {n}{2^{n-1}}}.}
В более общем случае для целого числа n > 0 [32]
sin ( n x ) = 2 n − 1 ∏ k = 0 n − 1 sin ( k n π + x ) = 2 n − 1 ∏ k = 1 n sin ( k n π − x ) . {\displaystyle \sin(nx)=2^{n-1}\prod _{k=0}^{n-1}\sin \left({\frac {k}{n}}\pi +x\right)=2^{n-1}\prod _{k=1}^{n}\sin \left({\frac {k}{n}}\pi -x\right).}
или записано в терминах функции аккорда , crd x ≡ 2 sin 1 2 x {\textstyle \operatorname {crd} x\equiv 2\sin {\tfrac {1}{2}}x}
crd ( n x ) = ∏ k = 1 n crd ( k n 2 π − x ) . {\displaystyle \operatorname {crd} (nx)=\prod _{k=1}^{n}\operatorname {crd} \left({\frac {k}{n}}2\pi -x\right).}
Это происходит из-за разложения многочлена на линейные множители (ср. корень из единицы ): Для любого комплексного z и целого числа n > 0 , z n − 1 {\textstyle z^{n}-1}
z n − 1 = ∏ k = 1 n ( z − exp ( k n 2 π i ) ) . {\displaystyle z^{n}-1=\prod _{k=1}^{n}\left(z-\exp {\Bigl (}{\frac {k}{n}}2\pi i{\Bigr )}\right).}
Линейные комбинации Для некоторых целей важно знать, что любая линейная комбинация синусоидальных волн с одинаковым периодом или частотой, но разными фазовыми сдвигами также является синусоидальной волной с одинаковым периодом или частотой, но разными фазовыми сдвигами. Это полезно при подгонке данных синусоиды , поскольку измеренные или наблюдаемые данные линейно связаны с неизвестными a и b базиса синфазных и квадратурных компонентов ниже, что приводит к более простому якобиану по сравнению с и . c {\displaystyle c} φ {\displaystyle \varphi }
Синус и косинус Линейная комбинация или гармоническое сложение синусоидальных и косинусоидальных волн эквивалентно одной синусоидальной волне со сдвигом фазы и масштабированной амплитудой, [33] [34]
a cos x + b sin x = c cos ( x + φ ) {\displaystyle a\cos x+b\sin x=c\cos(x+\varphi )}
где и определяются следующим образом: c {\displaystyle c} φ {\displaystyle \varphi }
c = sgn ( a ) a 2 + b 2 , φ = arctan ( − b / a ) , {\displaystyle {\begin{aligned}c&=\operatorname {sgn}(a){\sqrt {a^{2}+b^{2}}},\\\varphi &={\arctan }{\bigl (}{-b/a}{\bigr )},\end{aligned}}}
при условии a ≠ 0. {\displaystyle a\neq 0.}
Произвольный сдвиг фаз В более общем случае для произвольных фазовых сдвигов мы имеем
a sin ( x + θ a ) + b sin ( x + θ b ) = c sin ( x + φ ) {\displaystyle a\sin(x+\theta _{a})+b\sin(x+\theta _{b})=c\sin(x+\varphi )}
где и удовлетворяют: c {\displaystyle c} φ {\displaystyle \varphi }
c 2 = a 2 + b 2 + 2 a b cos ( θ a − θ b ) , tan φ = a sin θ a + b sin θ b a cos θ a + b cos θ b . {\displaystyle {\begin{aligned}c^{2}&=a^{2}+b^{2}+2ab\cos \left(\theta _{a}-\theta _{b}\right),\\\tan \varphi &={\frac {a\sin \theta _{a}+b\sin \theta _{b}}{a\cos \theta _{a}+b\cos \theta _{b}}}.\end{aligned}}}
Более двух синусоид Общий случай выглядит так [34]
∑ i a i sin ( x + θ i ) = a sin ( x + θ ) , {\displaystyle \sum _{i}a_{i}\sin(x+\theta _{i})=a\sin(x+\theta ),} a 2 = ∑ i , j a i a j cos ( θ i − θ j ) {\displaystyle a^{2}=\sum _{i,j}a_{i}a_{j}\cos(\theta _{i}-\theta _{j})} tan θ = ∑ i a i sin θ i ∑ i a i cos θ i . {\displaystyle \tan \theta ={\frac {\sum _{i}a_{i}\sin \theta _{i}}{\sum _{i}a_{i}\cos \theta _{i}}}.}
Эти тождества, названные в честь Жозефа Луи Лагранжа , таковы: [35] [36] [37]
для ∑ k = 0 n sin k θ = cos 1 2 θ − cos ( ( n + 1 2 ) θ ) 2 sin 1 2 θ ∑ k = 0 n cos k θ = sin 1 2 θ + sin ( ( n + 1 2 ) θ ) 2 sin 1 2 θ {\displaystyle {\begin{aligned}\sum _{k=0}^{n}\sin k\theta &={\frac {\cos {\tfrac {1}{2}}\theta -\cos \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\\[5pt]\sum _{k=0}^{n}\cos k\theta &={\frac {\sin {\tfrac {1}{2}}\theta +\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\end{aligned}}} θ ≢ 0 ( mod 2 π ) . {\displaystyle \theta \not \equiv 0{\pmod {2\pi }}.}
Связанная функция — ядро Дирихле :
D n ( θ ) = 1 + 2 ∑ k = 1 n cos k θ = sin ( ( n + 1 2 ) θ ) sin 1 2 θ . {\displaystyle D_{n}(\theta )=1+2\sum _{k=1}^{n}\cos k\theta ={\frac {\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{\sin {\tfrac {1}{2}}\theta }}.}
Подобная идентичность [38]
∑ k = 1 n cos ( 2 k − 1 ) α = sin ( 2 n α ) 2 sin α . {\displaystyle \sum _{k=1}^{n}\cos(2k-1)\alpha ={\frac {\sin(2n\alpha )}{2\sin \alpha }}.}
Доказательство следующее. Используя тождества суммы и разности углов,
давайте рассмотрим следующую формулу: sin ( A + B ) − sin ( A − B ) = 2 cos A sin B . {\displaystyle \sin(A+B)-\sin(A-B)=2\cos A\sin B.}
2 sin α ∑ k = 1 n cos ( 2 k − 1 ) α = 2 sin α cos α + 2 sin α cos 3 α + 2 sin α cos 5 α + … + 2 sin α cos ( 2 n − 1 ) α {\displaystyle 2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha =2\sin \alpha \cos \alpha +2\sin \alpha \cos 3\alpha +2\sin \alpha \cos 5\alpha +\ldots +2\sin \alpha \cos(2n-1)\alpha }
2 sin α ∑ k = 1 n cos ( 2 k − 1 ) α = ∑ k = 1 n ( sin ( 2 k α ) − sin ( 2 ( k − 1 ) α ) ) = ( sin 2 α − sin 0 ) + ( sin 4 α − sin 2 α ) + ( sin 6 α − sin 4 α ) + … + ( sin ( 2 n α ) − sin ( 2 ( n − 1 ) α ) ) = sin ( 2 n α ) . {\displaystyle {\begin{aligned}&2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha \\&\quad =\sum _{k=1}^{n}(\sin(2k\alpha )-\sin(2(k-1)\alpha ))\\&\quad =(\sin 2\alpha -\sin 0)+(\sin 4\alpha -\sin 2\alpha )+(\sin 6\alpha -\sin 4\alpha )+\ldots +(\sin(2n\alpha )-\sin(2(n-1)\alpha ))\\&\quad =\sin(2n\alpha ).\end{aligned}}}
Итак, деление этой формулы на завершает доказательство. 2 sin α {\displaystyle 2\sin \alpha }
Если задано дробно-линейным преобразованием
и аналогично
, то f ( x ) {\displaystyle f(x)} f ( x ) = ( cos α ) x − sin α ( sin α ) x + cos α , {\displaystyle f(x)={\frac {(\cos \alpha )x-\sin \alpha }{(\sin \alpha )x+\cos \alpha }},} g ( x ) = ( cos β ) x − sin β ( sin β ) x + cos β , {\displaystyle g(x)={\frac {(\cos \beta )x-\sin \beta }{(\sin \beta )x+\cos \beta }},} f ( g ( x ) ) = g ( f ( x ) ) = ( cos ( α + β ) ) x − sin ( α + β ) ( sin ( α + β ) ) x + cos ( α + β ) . {\displaystyle f{\big (}g(x){\big )}=g{\big (}f(x){\big )}={\frac {{\big (}\cos(\alpha +\beta ){\big )}x-\sin(\alpha +\beta )}{{\big (}\sin(\alpha +\beta ){\big )}x+\cos(\alpha +\beta )}}.}
Говоря короче, если мы оставим все как есть , то, что мы назвали выше, тогда α {\displaystyle \alpha } f α {\displaystyle f_{\alpha }} f {\displaystyle f} f α ∘ f β = f α + β . {\displaystyle f_{\alpha }\circ f_{\beta }=f_{\alpha +\beta }.}
Если - наклон прямой, то - наклон ее поворота на угол x {\displaystyle x} f ( x ) {\displaystyle f(x)} − α . {\displaystyle -\alpha .}
Связь с комплексной показательной функцией Формула Эйлера гласит, что для любого действительного числа x : [39]
где i — мнимая единица . Подстановка − x вместо x дает нам: e i x = cos x + i sin x , {\displaystyle e^{ix}=\cos x+i\sin x,} e − i x = cos ( − x ) + i sin ( − x ) = cos x − i sin x . {\displaystyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x.}
Эти два уравнения можно использовать для решения косинуса и синуса в терминах экспоненциальной функции . В частности, [40] [41] cos x = e i x + e − i x 2 {\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}} sin x = e i x − e − i x 2 i {\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}
Эти формулы полезны для доказательства многих других тригонометрических тождеств. Например, то, что e i ( θ + φ )e iθ e iφ
соз( θ + φ ) + я грех ( θ + φ ) = ( соз θ + я грех θ ) ( соз φ + я грех φ ) = ( соз θ соз φ - грех θ грех φ ) + я ( соз θ грех φ + грех θ соз φ ) .
То, что действительная часть левой стороны равна действительной части правой стороны, является формулой сложения углов для косинуса. Равенство мнимых частей дает формулу сложения углов для синуса.
В следующей таблице тригонометрические функции и обратные им функции выражены через показательную функцию и комплексный логарифм .
Функция Обратная функция [42] sin θ = e i θ − e − i θ 2 i {\displaystyle \sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}} arcsin x = − i ln ( i x + 1 − x 2 ) {\displaystyle \arcsin x=-i\,\ln \left(ix+{\sqrt {1-x^{2}}}\right)} cos θ = e i θ + e − i θ 2 {\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}} arccos x = − i ln ( x + x 2 − 1 ) {\displaystyle \arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)} tan θ = − i e i θ − e − i θ e i θ + e − i θ {\displaystyle \tan \theta =-i\,{\frac {e^{i\theta }-e^{-i\theta }}{e^{i\theta }+e^{-i\theta }}}} arctan x = i 2 ln ( i + x i − x ) {\displaystyle \arctan x={\frac {i}{2}}\ln \left({\frac {i+x}{i-x}}\right)} csc θ = 2 i e i θ − e − i θ {\displaystyle \csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}} arccsc x = − i ln ( i x + 1 − 1 x 2 ) {\displaystyle \operatorname {arccsc} x=-i\,\ln \left({\frac {i}{x}}+{\sqrt {1-{\frac {1}{x^{2}}}}}\right)} sec θ = 2 e i θ + e − i θ {\displaystyle \sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}} arcsec x = − i ln ( 1 x + i 1 − 1 x 2 ) {\displaystyle \operatorname {arcsec} x=-i\,\ln \left({\frac {1}{x}}+i{\sqrt {1-{\frac {1}{x^{2}}}}}\right)} cot θ = i e i θ + e − i θ e i θ − e − i θ {\displaystyle \cot \theta =i\,{\frac {e^{i\theta }+e^{-i\theta }}{e^{i\theta }-e^{-i\theta }}}} arccot x = i 2 ln ( x − i x + i ) {\displaystyle \operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {x-i}{x+i}}\right)} cis θ = e i θ {\displaystyle \operatorname {cis} \theta =e^{i\theta }} arccis x = − i ln x {\displaystyle \operatorname {arccis} x=-i\ln x}
Отношение к сложным гиперболическим функциям Тригонометрические функции могут быть выведены из гиперболических функций с комплексными аргументами. Формулы для соотношений приведены ниже [43] [44] . sin x = − i sinh ( i x ) cos x = cosh ( i x ) tan x = − i tanh ( i x ) cot x = i coth ( i x ) sec x = sech ( i x ) csc x = i csch ( i x ) {\displaystyle {\begin{aligned}\sin x&=-i\sinh(ix)\\\cos x&=\cosh(ix)\\\tan x&=-i\tanh(ix)\\\cot x&=i\coth(ix)\\\sec x&=\operatorname {sech} (ix)\\\csc x&=i\operatorname {csch} (ix)\\\end{aligned}}}
Расширение серии При использовании разложения в степенной ряд для определения тригонометрических функций получаются следующие тождества: [45]
sin x = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! , {\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},} cos x = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! . {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.}
Для приложений к специальным функциям полезны следующие формулы бесконечного произведения для тригонометрических функций: [46] [47]
sin x = x ∏ n = 1 ∞ ( 1 − x 2 π 2 n 2 ) , cos x = ∏ n = 1 ∞ ( 1 − x 2 π 2 ( n − 1 2 ) ) 2 ) , sinh x = x ∏ n = 1 ∞ ( 1 + x 2 π 2 n 2 ) , cosh x = ∏ n = 1 ∞ ( 1 + x 2 π 2 ( n − 1 2 ) ) 2 ) . {\displaystyle {\begin{aligned}\sin x&=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cos x&=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right),\\[10mu]\sinh x&=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cosh x&=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right).\end{aligned}}}
Обратные тригонометрические функции Следующие тождества дают результат составления тригонометрической функции с обратной тригонометрической функцией. [48]
sin ( arcsin x ) = x cos ( arcsin x ) = 1 − x 2 tan ( arcsin x ) = x 1 − x 2 sin ( arccos x ) = 1 − x 2 cos ( arccos x ) = x tan ( arccos x ) = 1 − x 2 x sin ( arctan x ) = x 1 + x 2 cos ( arctan x ) = 1 1 + x 2 tan ( arctan x ) = x sin ( arccsc x ) = 1 x cos ( arccsc x ) = x 2 − 1 x tan ( arccsc x ) = 1 x 2 − 1 sin ( arcsec x ) = x 2 − 1 x cos ( arcsec x ) = 1 x tan ( arcsec x ) = x 2 − 1 sin ( arccot x ) = 1 1 + x 2 cos ( arccot x ) = x 1 + x 2 tan ( arccot x ) = 1 x {\displaystyle {\begin{aligned}\sin(\arcsin x)&=x&\cos(\arcsin x)&={\sqrt {1-x^{2}}}&\tan(\arcsin x)&={\frac {x}{\sqrt {1-x^{2}}}}\\\sin(\arccos x)&={\sqrt {1-x^{2}}}&\cos(\arccos x)&=x&\tan(\arccos x)&={\frac {\sqrt {1-x^{2}}}{x}}\\\sin(\arctan x)&={\frac {x}{\sqrt {1+x^{2}}}}&\cos(\arctan x)&={\frac {1}{\sqrt {1+x^{2}}}}&\tan(\arctan x)&=x\\\sin(\operatorname {arccsc} x)&={\frac {1}{x}}&\cos(\operatorname {arccsc} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\tan(\operatorname {arccsc} x)&={\frac {1}{\sqrt {x^{2}-1}}}\\\sin(\operatorname {arcsec} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\cos(\operatorname {arcsec} x)&={\frac {1}{x}}&\tan(\operatorname {arcsec} x)&={\sqrt {x^{2}-1}}\\\sin(\operatorname {arccot} x)&={\frac {1}{\sqrt {1+x^{2}}}}&\cos(\operatorname {arccot} x)&={\frac {x}{\sqrt {1+x^{2}}}}&\tan(\operatorname {arccot} x)&={\frac {1}{x}}\\\end{aligned}}}
Взяв мультипликативную инверсию обеих сторон каждого из приведенных выше уравнений, получим уравнения для
Правая сторона приведенной выше формулы всегда будет перевернута. Например, уравнение для имеет вид:
в то время как уравнения для и имеют вид: csc = 1 sin , sec = 1 cos , and cot = 1 tan . {\displaystyle \csc ={\frac {1}{\sin }},\;\sec ={\frac {1}{\cos }},{\text{ and }}\cot ={\frac {1}{\tan }}.} cot ( arcsin x ) {\displaystyle \cot(\arcsin x)} cot ( arcsin x ) = 1 tan ( arcsin x ) = 1 x 1 − x 2 = 1 − x 2 x {\displaystyle \cot(\arcsin x)={\frac {1}{\tan(\arcsin x)}}={\frac {1}{\frac {x}{\sqrt {1-x^{2}}}}}={\frac {\sqrt {1-x^{2}}}{x}}} csc ( arccos x ) {\displaystyle \csc(\arccos x)} sec ( arccos x ) {\displaystyle \sec(\arccos x)} csc ( arccos x ) = 1 sin ( arccos x ) = 1 1 − x 2 and sec ( arccos x ) = 1 cos ( arccos x ) = 1 x . {\displaystyle \csc(\arccos x)={\frac {1}{\sin(\arccos x)}}={\frac {1}{\sqrt {1-x^{2}}}}\qquad {\text{ and }}\quad \sec(\arccos x)={\frac {1}{\cos(\arccos x)}}={\frac {1}{x}}.}
Следующие тождества подразумеваются тождествами отражения. Они выполняются всякий раз, когда находятся в областях соответствующих функций. x , r , s , − x , − r , and − s {\displaystyle x,r,s,-x,-r,{\text{ and }}-s} π 2 = arcsin ( x ) + arccos ( x ) = arctan ( r ) + arccot ( r ) = arcsec ( s ) + arccsc ( s ) π = arccos ( x ) + arccos ( − x ) = arccot ( r ) + arccot ( − r ) = arcsec ( s ) + arcsec ( − s ) 0 = arcsin ( x ) + arcsin ( − x ) = arctan ( r ) + arctan ( − r ) = arccsc ( s ) + arccsc ( − s ) {\displaystyle {\begin{alignedat}{9}{\frac {\pi }{2}}~&=~\arcsin(x)&&+\arccos(x)~&&=~\arctan(r)&&+\operatorname {arccot}(r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arccsc}(s)\\[0.4ex]\pi ~&=~\arccos(x)&&+\arccos(-x)~&&=~\operatorname {arccot}(r)&&+\operatorname {arccot}(-r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arcsec}(-s)\\[0.4ex]0~&=~\arcsin(x)&&+\arcsin(-x)~&&=~\arctan(r)&&+\arctan(-r)~&&=~\operatorname {arccsc}(s)&&+\operatorname {arccsc}(-s)\\[1.0ex]\end{alignedat}}}
Также, [49] arctan x + arctan 1 x = { π 2 , if x > 0 − π 2 , if x < 0 arccot x + arccot 1 x = { π 2 , if x > 0 3 π 2 , if x < 0 {\displaystyle {\begin{aligned}\arctan x+\arctan {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\-{\frac {\pi }{2}},&{\text{if }}x<0\end{cases}}\\\operatorname {arccot} x+\operatorname {arccot} {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\{\frac {3\pi }{2}},&{\text{if }}x<0\end{cases}}\\\end{aligned}}} arccos 1 x = arcsec x and arcsec 1 x = arccos x {\displaystyle \arccos {\frac {1}{x}}=\operatorname {arcsec} x\qquad {\text{ and }}\qquad \operatorname {arcsec} {\frac {1}{x}}=\arccos x} arcsin 1 x = arccsc x and arccsc 1 x = arcsin x {\displaystyle \arcsin {\frac {1}{x}}=\operatorname {arccsc} x\qquad {\text{ and }}\qquad \operatorname {arccsc} {\frac {1}{x}}=\arcsin x}
Функцию арктангенса можно разложить в ряд: [50] arctan ( n x ) = ∑ m = 1 n arctan x 1 + ( m − 1 ) m x 2 {\displaystyle \arctan(nx)=\sum _{m=1}^{n}\arctan {\frac {x}{1+(m-1)mx^{2}}}}
Идентичности без переменных В терминах функции арктангенса имеем [49] arctan 1 2 = arctan 1 3 + arctan 1 7 . {\displaystyle \arctan {\frac {1}{2}}=\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}
Любопытное тождество, известное как закон Морри , cos 20 ∘ ⋅ cos 40 ∘ ⋅ cos 80 ∘ = 1 8 , {\displaystyle \cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}},}
является частным случаем тождества, содержащего одну переменную: ∏ j = 0 k − 1 cos ( 2 j x ) = sin ( 2 k x ) 2 k sin x . {\displaystyle \prod _{j=0}^{k-1}\cos \left(2^{j}x\right)={\frac {\sin \left(2^{k}x\right)}{2^{k}\sin x}}.}
Аналогично,
есть частный случай тождества с : sin 20 ∘ ⋅ sin 40 ∘ ⋅ sin 80 ∘ = 3 8 {\displaystyle \sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\frac {\sqrt {3}}{8}}} x = 20 ∘ {\displaystyle x=20^{\circ }} sin x ⋅ sin ( 60 ∘ − x ) ⋅ sin ( 60 ∘ + x ) = sin 3 x 4 . {\displaystyle \sin x\cdot \sin \left(60^{\circ }-x\right)\cdot \sin \left(60^{\circ }+x\right)={\frac {\sin 3x}{4}}.}
Для этого случая , x = 15 ∘ {\displaystyle x=15^{\circ }} sin 15 ∘ ⋅ sin 45 ∘ ⋅ sin 75 ∘ = 2 8 , sin 15 ∘ ⋅ sin 75 ∘ = 1 4 . {\displaystyle {\begin{aligned}\sin 15^{\circ }\cdot \sin 45^{\circ }\cdot \sin 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\sin 15^{\circ }\cdot \sin 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}
Для этого случая , x = 10 ∘ {\displaystyle x=10^{\circ }} sin 10 ∘ ⋅ sin 50 ∘ ⋅ sin 70 ∘ = 1 8 . {\displaystyle \sin 10^{\circ }\cdot \sin 50^{\circ }\cdot \sin 70^{\circ }={\frac {1}{8}}.}
То же самое тождество косинуса cos x ⋅ cos ( 60 ∘ − x ) ⋅ cos ( 60 ∘ + x ) = cos 3 x 4 . {\displaystyle \cos x\cdot \cos \left(60^{\circ }-x\right)\cdot \cos \left(60^{\circ }+x\right)={\frac {\cos 3x}{4}}.}
Сходным образом, cos 10 ∘ ⋅ cos 50 ∘ ⋅ cos 70 ∘ = 3 8 , cos 15 ∘ ⋅ cos 45 ∘ ⋅ cos 75 ∘ = 2 8 , cos 15 ∘ ⋅ cos 75 ∘ = 1 4 . {\displaystyle {\begin{aligned}\cos 10^{\circ }\cdot \cos 50^{\circ }\cdot \cos 70^{\circ }&={\frac {\sqrt {3}}{8}},\\\cos 15^{\circ }\cdot \cos 45^{\circ }\cdot \cos 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\cos 15^{\circ }\cdot \cos 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}
Сходным образом, tan 50 ∘ ⋅ tan 60 ∘ ⋅ tan 70 ∘ = tan 80 ∘ , tan 40 ∘ ⋅ tan 30 ∘ ⋅ tan 20 ∘ = tan 10 ∘ . {\displaystyle {\begin{aligned}\tan 50^{\circ }\cdot \tan 60^{\circ }\cdot \tan 70^{\circ }&=\tan 80^{\circ },\\\tan 40^{\circ }\cdot \tan 30^{\circ }\cdot \tan 20^{\circ }&=\tan 10^{\circ }.\end{aligned}}}
Следующее утверждение, возможно, не так легко обобщить на тождество, содержащее переменные (но см. объяснение ниже): cos 24 ∘ + cos 48 ∘ + cos 96 ∘ + cos 168 ∘ = 1 2 . {\displaystyle \cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.}
Градусная мера перестает быть более удачной, чем радианная мера, если учесть это тождество с 21 в знаменателе: cos 2 π 21 + cos ( 2 ⋅ 2 π 21 ) + cos ( 4 ⋅ 2 π 21 ) + cos ( 5 ⋅ 2 π 21 ) + cos ( 8 ⋅ 2 π 21 ) + cos ( 10 ⋅ 2 π 21 ) = 1 2 . {\displaystyle \cos {\frac {2\pi }{21}}+\cos \left(2\cdot {\frac {2\pi }{21}}\right)+\cos \left(4\cdot {\frac {2\pi }{21}}\right)+\cos \left(5\cdot {\frac {2\pi }{21}}\right)+\cos \left(8\cdot {\frac {2\pi }{21}}\right)+\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.}
Множители 1, 2, 4, 5, 8, 10 могут начать прояснять закономерность: это те целые числа, которые меньше 21 / 2 взаимно просты (или не имеют общих простых множителей с) 21. Последние несколько примеров являются следствиями основного факта о неприводимых циклотомических многочленах : косинусы являются действительными частями нулей этих многочленов; сумма нулей является функцией Мёбиуса , вычисленной в (в самом последнем случае выше) 21; только половина нулей присутствует выше. Два тождества, предшествующие этому последнему, возникают таким же образом с заменой 21 на 10 и 15 соответственно.
Другие тождества косинуса включают в себя: [51]
и так далее для всех нечетных чисел, и, следовательно, 2 cos π 3 = 1 , 2 cos π 5 × 2 cos 2 π 5 = 1 , 2 cos π 7 × 2 cos 2 π 7 × 2 cos 3 π 7 = 1 , {\displaystyle {\begin{aligned}2\cos {\frac {\pi }{3}}&=1,\\2\cos {\frac {\pi }{5}}\times 2\cos {\frac {2\pi }{5}}&=1,\\2\cos {\frac {\pi }{7}}\times 2\cos {\frac {2\pi }{7}}\times 2\cos {\frac {3\pi }{7}}&=1,\end{aligned}}} cos π 3 + cos π 5 × cos 2 π 5 + cos π 7 × cos 2 π 7 × cos 3 π 7 + ⋯ = 1. {\displaystyle \cos {\frac {\pi }{3}}+\cos {\frac {\pi }{5}}\times \cos {\frac {2\pi }{5}}+\cos {\frac {\pi }{7}}\times \cos {\frac {2\pi }{7}}\times \cos {\frac {3\pi }{7}}+\dots =1.}
Многие из этих любопытных идентичностей вытекают из более общих фактов, таких как следующие: [52]
и ∏ k = 1 n − 1 sin k π n = n 2 n − 1 {\displaystyle \prod _{k=1}^{n-1}\sin {\frac {k\pi }{n}}={\frac {n}{2^{n-1}}}} ∏ k = 1 n − 1 cos k π n = sin π n 2 2 n − 1 . {\displaystyle \prod _{k=1}^{n-1}\cos {\frac {k\pi }{n}}={\frac {\sin {\frac {\pi n}{2}}}{2^{n-1}}}.}
Объединив их, мы получаем ∏ k = 1 n − 1 tan k π n = n sin π n 2 {\displaystyle \prod _{k=1}^{n-1}\tan {\frac {k\pi }{n}}={\frac {n}{\sin {\frac {\pi n}{2}}}}}
Если n — нечетное число ( ), мы можем использовать симметрии, чтобы получить n = 2 m + 1 {\displaystyle n=2m+1} ∏ k = 1 m tan k π 2 m + 1 = 2 m + 1 {\displaystyle \prod _{k=1}^{m}\tan {\frac {k\pi }{2m+1}}={\sqrt {2m+1}}}
Передаточная функция фильтра нижних частот Баттерворта может быть выражена через полином и полюса. Задавая частоту как частоту среза, можно доказать следующее тождество: ∏ k = 1 n sin ( 2 k − 1 ) π 4 n = ∏ k = 1 n cos ( 2 k − 1 ) π 4 n = 2 2 n {\displaystyle \prod _{k=1}^{n}\sin {\frac {\left(2k-1\right)\pi }{4n}}=\prod _{k=1}^{n}\cos {\frac {\left(2k-1\right)\pi }{4n}}={\frac {\sqrt {2}}{2^{n}}}}
π Эффективный способ вычисления π с большим количеством цифр основан на следующем тождестве без переменных, предложенном Мачиным . Это известно как формула типа Мачиного :
или, альтернативно, с использованием тождества Леонарда Эйлера :
или с использованием пифагорейских троек : π 4 = 4 arctan 1 5 − arctan 1 239 {\displaystyle {\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}} π 4 = 5 arctan 1 7 + 2 arctan 3 79 {\displaystyle {\frac {\pi }{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}} π = arccos 4 5 + arccos 5 13 + arccos 16 65 = arcsin 3 5 + arcsin 12 13 + arcsin 63 65 . {\displaystyle \pi =\arccos {\frac {4}{5}}+\arccos {\frac {5}{13}}+\arccos {\frac {16}{65}}=\arcsin {\frac {3}{5}}+\arcsin {\frac {12}{13}}+\arcsin {\frac {63}{65}}.}
Другие включают: [53] [49] π 4 = arctan 1 2 + arctan 1 3 , {\displaystyle {\frac {\pi }{4}}=\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}},} π = arctan 1 + arctan 2 + arctan 3 , {\displaystyle \pi =\arctan 1+\arctan 2+\arctan 3,} π 4 = 2 arctan 1 3 + arctan 1 7 . {\displaystyle {\frac {\pi }{4}}=2\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}
В общем случае для чисел t 1 , ..., t n −1θ n n −1 к =1t k π /4, 3 π /4)t n π /2 − θ n θ n t 1 , ..., t n −1 ,(−1, 1) . В частности, вычисленное t n t 1 , ..., t n −1 π 2 = ∑ k = 1 n arctan ( t k ) π = ∑ k = 1 n sgn ( t k ) arccos ( 1 − t k 2 1 + t k 2 ) π = ∑ k = 1 n arcsin ( 2 t k 1 + t k 2 ) π = ∑ k = 1 n arctan ( 2 t k 1 − t k 2 ) , {\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\sum _{k=1}^{n}\arctan(t_{k})\\\pi &=\sum _{k=1}^{n}\operatorname {sgn}(t_{k})\arccos \left({\frac {1-t_{k}^{2}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arcsin \left({\frac {2t_{k}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arctan \left({\frac {2t_{k}}{1-t_{k}^{2}}}\right)\,,\end{aligned}}}
где во всех выражениях, кроме первого, мы использовали формулы тангенса половинного угла. Первые две формулы работают, даже если одно или несколько значений t k (−1, 1) . Обратите внимание, что если t = p / q (2 t , 1 − t 2 , 1 + t 2 ) в приведенных выше формулах пропорциональны пифагоровой тройке (2 pq , q 2 − p 2 , q 2 + p 2 ) .
Например, для n = 3a , b , c , d > 0 . π 2 = arctan ( a b ) + arctan ( c d ) + arctan ( b d − a c a d + b c ) {\displaystyle {\frac {\pi }{2}}=\arctan \left({\frac {a}{b}}\right)+\arctan \left({\frac {c}{d}}\right)+\arctan \left({\frac {bd-ac}{ad+bc}}\right)}
Тождество Евклида Евклид показал в Книге XIII, Предложении 10 своих Элементов sin 2 18 ∘ + sin 2 30 ∘ = sin 2 36 ∘ . {\displaystyle \sin ^{2}18^{\circ }+\sin ^{2}30^{\circ }=\sin ^{2}36^{\circ }.}
Птолемей использовал это предложение для вычисления некоторых углов в своей таблице хорд в книге I, главе 11 Альмагеста
Состав тригонометрических функций Эти тождества включают тригонометрическую функцию тригонометрической функции: [54]
cos ( t sin x ) = J 0 ( t ) + 2 ∑ k = 1 ∞ J 2 k ( t ) cos ( 2 k x ) {\displaystyle \cos(t\sin x)=J_{0}(t)+2\sum _{k=1}^{\infty }J_{2k}(t)\cos(2kx)} sin ( t sin x ) = 2 ∑ k = 0 ∞ J 2 k + 1 ( t ) sin ( ( 2 k + 1 ) x ) {\displaystyle \sin(t\sin x)=2\sum _{k=0}^{\infty }J_{2k+1}(t)\sin {\big (}(2k+1)x{\big )}} cos ( t cos x ) = J 0 ( t ) + 2 ∑ k = 1 ∞ ( − 1 ) k J 2 k ( t ) cos ( 2 k x ) {\displaystyle \cos(t\cos x)=J_{0}(t)+2\sum _{k=1}^{\infty }(-1)^{k}J_{2k}(t)\cos(2kx)} sin ( t cos x ) = 2 ∑ k = 0 ∞ ( − 1 ) k J 2 k + 1 ( t ) cos ( ( 2 k + 1 ) x ) {\displaystyle \sin(t\cos x)=2\sum _{k=0}^{\infty }(-1)^{k}J_{2k+1}(t)\cos {\big (}(2k+1)x{\big )}} где J i — функции Бесселя .
α +β +γ = 180°Условное тригонометрическое тождество — это тригонометрическое тождество, которое выполняется, если выполняются указанные условия для аргументов тригонометрических функций. [55] Следующие формулы применимы к произвольным плоским треугольникам и вытекают из того, что функции, встречающиеся в формулах, хорошо определены (последнее применимо только к формулам, в которых встречаются тангенсы и котангенсы). α + β + γ = 180 ∘ , {\displaystyle \alpha +\beta +\gamma =180^{\circ },} tan α + tan β + tan γ = tan α tan β tan γ 1 = cot β cot γ + cot γ cot α + cot α cot β cot ( α 2 ) + cot ( β 2 ) + cot ( γ 2 ) = cot ( α 2 ) cot ( β 2 ) cot ( γ 2 ) 1 = tan ( β 2 ) tan ( γ 2 ) + tan ( γ 2 ) tan ( α 2 ) + tan ( α 2 ) tan ( β 2 ) sin α + sin β + sin γ = 4 cos ( α 2 ) cos ( β 2 ) cos ( γ 2 ) − sin α + sin β + sin γ = 4 cos ( α 2 ) sin ( β 2 ) sin ( γ 2 ) cos α + cos β + cos γ = 4 sin ( α 2 ) sin ( β 2 ) sin ( γ 2 ) + 1 − cos α + cos β + cos γ = 4 sin ( α 2 ) cos ( β 2 ) cos ( γ 2 ) − 1 sin ( 2 α ) + sin ( 2 β ) + sin ( 2 γ ) = 4 sin α sin β sin γ − sin ( 2 α ) + sin ( 2 β ) + sin ( 2 γ ) = 4 sin α cos β cos γ cos ( 2 α ) + cos ( 2 β ) + cos ( 2 γ ) = − 4 cos α cos β cos γ − 1 − cos ( 2 α ) + cos ( 2 β ) + cos ( 2 γ ) = − 4 cos α sin β sin γ + 1 sin 2 α + sin 2 β + sin 2 γ = 2 cos α cos β cos γ + 2 − sin 2 α + sin 2 β + sin 2 γ = 2 cos α sin β sin γ cos 2 α + cos 2 β + cos 2 γ = − 2 cos α cos β cos γ + 1 − cos 2 α + cos 2 β + cos 2 γ = − 2 cos α sin β sin γ + 1 sin 2 ( 2 α ) + sin 2 ( 2 β ) + sin 2 ( 2 γ ) = − 2 cos ( 2 α ) cos ( 2 β ) cos ( 2 γ ) + 2 cos 2 ( 2 α ) + cos 2 ( 2 β ) + cos 2 ( 2 γ ) = 2 cos ( 2 α ) cos ( 2 β ) cos ( 2 γ ) + 1 1 = sin 2 ( α 2 ) + sin 2 ( β 2 ) + sin 2 ( γ 2 ) + 2 sin ( α 2 ) sin ( β 2 ) sin ( γ 2 ) {\displaystyle {\begin{aligned}\tan \alpha +\tan \beta +\tan \gamma &=\tan \alpha \tan \beta \tan \gamma \\1&=\cot \beta \cot \gamma +\cot \gamma \cot \alpha +\cot \alpha \cot \beta \\\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\beta }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)&=\cot \left({\frac {\alpha }{2}}\right)\cot \left({\frac {\beta }{2}}\right)\cot \left({\frac {\gamma }{2}}\right)\\1&=\tan \left({\frac {\beta }{2}}\right)\tan \left({\frac {\gamma }{2}}\right)+\tan \left({\frac {\gamma }{2}}\right)\tan \left({\frac {\alpha }{2}}\right)+\tan \left({\frac {\alpha }{2}}\right)\tan \left({\frac {\beta }{2}}\right)\\\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)\\-\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)\\\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)+1\\-\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)-1\\\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \sin \beta \sin \gamma \\-\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \cos \beta \cos \gamma \\\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \cos \beta \cos \gamma -1\\-\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \cos \beta \cos \gamma +2\\-\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \sin \beta \sin \gamma \\\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \cos \beta \cos \gamma +1\\-\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}(2\alpha )+\sin ^{2}(2\beta )+\sin ^{2}(2\gamma )&=-2\cos(2\alpha )\cos(2\beta )\cos(2\gamma )+2\\\cos ^{2}(2\alpha )+\cos ^{2}(2\beta )+\cos ^{2}(2\gamma )&=2\cos(2\alpha )\,\cos(2\beta )\,\cos(2\gamma )+1\\1&=\sin ^{2}\left({\frac {\alpha }{2}}\right)+\sin ^{2}\left({\frac {\beta }{2}}\right)+\sin ^{2}\left({\frac {\gamma }{2}}\right)+2\sin \left({\frac {\alpha }{2}}\right)\,\sin \left({\frac {\beta }{2}}\right)\,\sin \left({\frac {\gamma }{2}}\right)\end{aligned}}}
Исторические стенографии Версинус , коверсинус , гаверсинус и экссеканс использовались в навигации. Например, формула гаверсинуса использовалась для вычисления расстояния между двумя точками на сфере. Сегодня они используются редко .
Разнообразный
ядро Дирихле Ядро Дирихле D n ( x ) 1 + 2 cos x + 2 cos ( 2 x ) + 2 cos ( 3 x ) + ⋯ + 2 cos ( n x ) = sin ( ( n + 1 2 ) x ) sin ( 1 2 x ) . {\displaystyle 1+2\cos x+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin \left({\frac {1}{2}}x\right)}}.}
Свертка любой интегрируемой функции периода с ядром Дирихле совпадает с Фурье-аппроксимацией функции th-й степени. То же самое справедливо для любой меры или обобщенной функции . 2 π {\displaystyle 2\pi } n {\displaystyle n}
Замена половинного угла тангенса Если мы установим то [56]
, где иногда сокращается до цис x t = tan x 2 , {\displaystyle t=\tan {\frac {x}{2}},} sin x = 2 t 1 + t 2 ; cos x = 1 − t 2 1 + t 2 ; e i x = 1 + i t 1 − i t ; d x = 2 d t 1 + t 2 , {\displaystyle \sin x={\frac {2t}{1+t^{2}}};\qquad \cos x={\frac {1-t^{2}}{1+t^{2}}};\qquad e^{ix}={\frac {1+it}{1-it}};\qquad dx={\frac {2\,dt}{1+t^{2}}},} e i x = cos x + i sin x , {\displaystyle e^{ix}=\cos x+i\sin x,}
Когда эта замена на tan t {\displaystyle t} х / 2 исчислении , следует, чтозаменяется на sin x {\displaystyle \sin x} 2 т / 1 + т 2 cos x {\displaystyle \cos x} 1 − т 2 / 1 + т 2 d x заменяется на 2 д т / 1 + т 2 первообразные . sin x {\displaystyle \sin x} cos x {\displaystyle \cos x} t {\displaystyle t}
cos θ 2 ⋅ cos θ 4 ⋅ cos θ 8 ⋯ = ∏ n = 1 ∞ cos θ 2 n = sin θ θ = sinc θ . {\displaystyle \cos {\frac {\theta }{2}}\cdot \cos {\frac {\theta }{4}}\cdot \cos {\frac {\theta }{8}}\cdots =\prod _{n=1}^{\infty }\cos {\frac {\theta }{2^{n}}}={\frac {\sin \theta }{\theta }}=\operatorname {sinc} \theta .}
Смотрите также
Ссылки ^ Абрамовиц, Милтон ; Стиган, Ирен Энн , ред. (1983) [июнь 1964]. "Глава 4, уравнение 4.3.45". Справочник по математическим функциям с формулами, графиками и математическими таблицами ISBN 978-0-486-61272-0 LCCN 64-60036. MR 0167642. LCCN 65-12253.^ Селби 1970, стр. 188 ^ Абрамовиц и Стегун, с. 72, 4.3.13–15 ^ Абрамовиц и Стегун, с. 72, 4.3.7–9 ^ Абрамовиц и Стегун, с. 72, 4.3.16 ^ abcd Вайсштейн, Эрик В. «Тригонометрические формулы сложения». MathWorld . ^ Абрамовиц и Стегун, с. 72, 4.3.17 ^ Абрамовиц и Стегун, с. 72, 4.3.18 ^ ab "Тождества суммы и разности углов". www.milefoot.com . Получено 12 октября 2019 г. ^ Абрамовиц и Стегун, с. 72, 4.3.19 ^ Абрамовиц и Стегун, с. 80, 4.4.32 ^ Абрамовиц и Стегун, с. 80, 4.4.33 ^ Абрамовиц и Стегун, с. 80, 4.4.34 ^ Бронштейн, Мануэль (1989). «Упрощение действительных элементарных функций». В Gonnet, GH (ред.). Труды Международного симпозиума ACM- SIGSAM 1989 по символическим и алгебраическим вычислениям . ISSAC '89 (Портленд, США, штат Орегон, 1989-07). Нью-Йорк: ACM . С. 207–211 . doi :10.1145/74540.74566. ISBN 0-89791-325-6 ^ Майкл Харди. (2016). «О касательных и секущих бесконечных сумм». The American Mathematical Monthly , том 123, номер 7, 701–703. https://doi.org/10.4169/amer.math.monthly.123.7.701 ^ Харди, Майкл (2016). «О касательных и секущих бесконечных сумм». American Mathematical Monthly . 123 (7): 701– 703. doi :10.4169/amer.math.monthly.123.7.701. ^ ab «Синус, косинус и теорема Птолемея». ^ аб Вайсштейн, Эрик В. «Формулы нескольких углов». Математический мир . ^ Абрамовиц и Стегун, с. 74, 4.3.48 ^ ab Selby 1970, стр. 190 ^ Weisstein, Eric W. "Multiple-Angle Formulas". mathworld.wolfram.com . Получено 2022-02-06 . ^ Уорд, Кен. "Рекурсивная формула для нескольких углов". Страницы математики Кена Уорда . ^ ab Abramowitz, Milton ; Stegun, Irene Ann , ред. (1983) [июнь 1964]. "Глава 4, уравнение 4.3.20-22". Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия Applied Mathematics. Том 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. стр. 72. ISBN 978-0-486-61272-0 LCCN 64-60036. MR 0167642. LCCN 65-12253.^ аб Вайсштейн, Эрик В. «Формулы половинного угла». Математический мир . ^ Абрамовиц и Стегун, с. 72, 4.3.24–26 ^ Вайсштейн, Эрик В. «Формулы двойного угла». MathWorld . ^ Абрамовиц и Стегун, с. 72, 4.3.27–28 ^ Абрамовиц и Стегун, с. 72, 4.3.31–33 ^ Ивс, Говард (1990). Введение в историю математики (6-е изд.). Филадельфия: Saunders College Pub. стр. 309. ISBN 0-03-029558-0 OCLC 20842510.^ Абрамовиц и Стегун, с. 72, 4.3.34–39 ^ Джонсон, Уоррен П. (апрель 2010 г.). «Тригонометрические тождества в духе Эрмита». American Mathematical Monthly . 117 (4): 311– 327. doi :10.4169/000298910x480784. S2CID 29690311. ^ «Идентификация продукта под разными углами». ^ Апостол, ТМ (1967) Исчисление. 2-е издание. Нью-Йорк, Нью-Йорк, Wiley. С. 334-335. ^ ab Weisstein, Eric W. «Теорема о гармоническом сложении». MathWorld . ^ Ортис Муньис, Эдди (февраль 1953 г.). «Метод вывода различных формул в электростатике и электромагнетизме с использованием тригонометрических тождеств Лагранжа». American Journal of Physics . 21 (2): 140. Bibcode : 1953AmJPh..21..140M. doi : 10.1119/1.1933371. ^ Агарвал, Рави П.; О'Реган, Донал (2008). Обыкновенные и частные дифференциальные уравнения: со специальными функциями, рядами Фурье и граничными задачами (иллюстрированное издание). Springer Science & Business Media. стр. 185. ISBN 978-0-387-79146-3 ^ Джеффри, Алан; Дай, Хуэй-хуэй (2008). "Раздел 2.4.1.6". Справочник по математическим формулам и интегралам (4-е изд.). Academic Press. ISBN 978-0-12-374288-9 ^ Фэй, Темпл Х.; Клопперс, П. Хендрик (2001). «Феномен Гиббса». Международный журнал математического образования в науке и технике . 32 (1): 73– 89. doi :10.1080/00207390117151. ^ Абрамовиц и Стегун, с. 74, 4.3.47 ^ Абрамовиц и Стегун, с. 71, 4.3.2 ^ Абрамовиц и Стегун, с. 71, 4.3.1 ^ Абрамовиц и Стегун, с. 80, 4.4.26–31 ^ Хокинс, Фейт Мэри; Хокинс, Дж. К. (1 марта 1969 г.). Комплексные числа и элементарные комплексные функции. Лондон: MacDonald Technical & Scientific London (опубликовано в 1968 г.). стр. 122. ISBN 978-0356025056 {{cite book }}: CS1 maint: date and year (link )^ Маркушевич, А.И. (1966). Замечательная функция синуса. Нью-Йорк: American Elsevier Publishing Company, Inc. стр. 35–37 , 81. ISBN 978-1483256313 ^ Абрамовиц и Стегун, с. 74, 4.3.65–66 ^ Абрамовиц и Стегун, с. 75, 4.3.89–90 ^ Абрамовиц и Стегун, с. 85, 4.5.68–69 ^ Абрамовиц и Стегун 1972, стр. 73, 4.3.45 ^ abc Wu, Rex H. «Доказательство без слов: тождество арктангенса Эйлера», Mathematics Magazine 77(3), июнь 2004 г., стр. 189. ^ SM Abrarov, RK Jagpal, R. Siddiqui и BM Quine (2021), «Алгоритмическое определение большого целого числа в двухчленной формуле типа Мачина для π», Mathematics , 9 (17), 2162, arXiv : 2107.01027 , doi : 10.3390/math9172162 {{citation }}: CS1 maint: multiple names: authors list (link )↑ Хамбл, Стив (ноябрь 2004 г.). «Идентичность бабушки». Mathematical Gazette . 88 : 524– 525. doi :10.1017/s0025557200176223. S2CID 125105552. ^ Вайсштейн, Эрик В. «Синус». MathWorld . ^ Харрис, Эдвард М. «Суммы арктангенсов», в книге Роджера Б. Нельсона « Доказательства без слов» (1993, Математическая ассоциация Америки), стр. 39. ↑ Милтон Абрамовиц и Ирен Стиган, Справочник по математическим функциям с формулами, графиками и математическими таблицами , Dover Publications , Нью-Йорк, 1972, формулы 9.1.42–9.1.45^ Эр. К.С. Джоши, ИИТ Кришны МАТЕМАТИКА . Кришна Пракашан Медиа. Меерут, Индия. страница 636. ^ Абрамовиц и Стегун, с. 72, 4.3.23
Библиография Абрамовиц, Милтон ; Стиган, Ирен А. , ред. (1972). Справочник по математическим функциям с формулами, графиками и математическими таблицами. Нью-Йорк: Dover Publications . ISBN 978-0-486-61272-0 Нильсен, Кай Л. (1966), Логарифмические и тригонометрические таблицы до пяти знаков (2-е изд.), Нью-Йорк: Barnes & Noble , LCCN 61-9103 Селби, Сэмюэл М., ред. (1970), Стандартные математические таблицы (18-е изд.), The Chemical Rubber Co.
Внешние ссылки Значения sin и cos, выраженные в иррациональных дробях, для целых кратных 3° и 5+5/8°, а также для тех же углов csc и sec и tan 





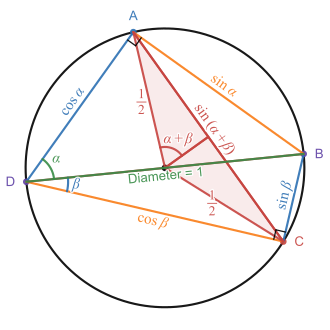


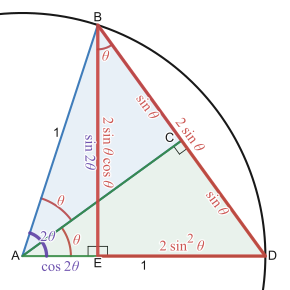

























































































































![{\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14cc79239a0fcdfb53b132d75a93474e9e6d5ba0)

![{\displaystyle ({-\пи},\пи],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/122328145a5f3a4162d21b4fbb5f4d1149932d2b)






































![{\displaystyle {\begin{align}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1927ae2be96f5156e18813a20486fdb0ff72f1)
![{\displaystyle {\begin{aligned}{\tan}{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {{\sin}{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\[10pt]&={\frac {\displaystyle \sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\[10pt]{\cot }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02567417a5a013481366384787e518cd74c68be)
![{\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9196b8ab5e0aef6cf7d7fec7d7546f2a6e7d2f)
![{\displaystyle {\begin{align}{\sec}{\Bigl (}\sum _{i}\theta _{i}{\Bigr)}&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots}}\\[8pt]{\csc}{\Bigl (}\sum _{i}\theta _{i}{\Bigr)}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots}}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24f2b169fbe11608507c63f5bb728e03b2b4957)


![{\displaystyle {\begin{align}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e082e69aab7a9c782f590f3a93262ba3101899b7)




























































![{\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\[3pt]\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\[3pt]\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\[6mu]&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\[3pt]\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d104c73c4b28f1dd7bfa5d2b0c7207c68cd87)
![{\displaystyle {\begin{align}\tan {\frac {\eta \pm \theta }{2}}&={\frac {\sin \eta \pm \sin \theta }{\cos \eta +\cos \theta }}\\[3pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[3pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639270245e163f1afa8682ac8aa12086db43dce1)








![{\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \, {\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1+\cos \theta }}\\[3pt]&={\frac {1-\cos \theta }{\sin \theta }}\\[5pt]\tan {\frac {\eta +\theta }{2}}&={\frac {\sin \eta +\sin \theta }{\cos \eta +\cos \theta }}\\[5pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[5pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\\[5pt]\tan {\frac {\theta }{2}}&={\frac {\tan \theta }{1+{\sqrt {1+\tan ^{2}\theta }}}}\\&{\text{for }}\theta \in \left(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cab50a58d64b8c3341fb4f7646888bbbc67ea0c)
![{\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \, {\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1-\cos \theta }}\\[4pt]&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c9be831a310f112ffc6e5790bc705dc7b070b87)










































![{\displaystyle {\begin{aligned}\cos \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )+\cos(\theta +\varphi ){\bigr )}\\[3mu]\sin \theta \,\sin \varphi &= {\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )-\cos(\theta +\varphi ){\bigr )}\\[3mu]\sin \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )+\sin(\theta -\варфи ){\bigr )}\\[3mu]\cos \theta \,\sin \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )-\sin(\theta -\varphi ){\bigr )}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa5a52add0153b90bd4863677fe0eab2f1700561)


![{\displaystyle {\begin{align}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\\[6pt]&{\text{где }}e=(e_{1},\ldots ,e_{n})\in S=\{1,-1\}^{n}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce2126a8ded0d0c92cf2bc4e9386c34430513c4b)







































![{\displaystyle {\begin{align}\sum _{k=0}^{n}\sin k\theta &={\frac {\cos {\tfrac {1}{2}}\theta -\cos \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\\[5pt]\sum _{k=0}^{n}\cos k\theta &={\frac {\sin {\tfrac {1}{2}}\theta +\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c850aa2dd7cc306d87d5d68d5802cab64f8572a0)




































![{\displaystyle {\begin{aligned}\sin x&=x\prod _{n=1}^{\infty}\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cos x&=\prod _{n=1}^{\infty}\left(1-{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right),\\[10mu]\sinh x&=x\prod _{n=1}^{\infty}\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cosh x&=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right).\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d43e1176a38b1e6b653837eb782ae79735783ac)








![{\displaystyle {\begin{alignedat}{9}{\frac {\pi }{2}}~&=~\arcsin(x)&&+\arccos(x)~&&=~\arctan(r)&&+\operatorname {arccot}(r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arccsc}(s)\\[0.4ex]\pi ~&=~\arccos(x)&&+\arccos(-x)~&&=~\operatorname {arccot}(r)&&+\operatorname {arccot}(-r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arcsec}(-s)\\[0.4ex]0~&=~\arcsin(x)&&+\arcsin(-x)~&&=~\arctan(r)&&+\arctan(-r)~&&=~\имя_оператора {arccsc}(s)&&+\имя_оператора {arccsc}(-s)\\[1.0ex]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/839db041f421b4af5890106450e2b4d3e9e183d4)
















































