5
| ||||
|---|---|---|---|---|
| Кардинал | пять | |||
| Порядковый | 5-й (пятый) | |||
| Система счисления | пятеричный | |||
| Факторизация | основной | |||
| Основной | 3-й | |||
| Делители | 1, 5 | |||
| греческое число | Э´ | |||
| римская цифра | В, в | |||
| греческий префикс | пента-/пент- | |||
| латинский префикс | куинке-/куинку-/квинт- | |||
| Двоичный | 101 2 | |||
| Тройной | 12 3 | |||
| Шенерный | 5 6 | |||
| Восьмеричный | 5 8 | |||
| Двенадцатеричная система счисления | 5 12 | |||
| Шестнадцатеричный | 5 16 | |||
| греческий | ε (или Ε) | |||
| арабский , курдский | 5 | |||
| Персидский , Синдхи , Урду | 5 | |||
| Геэз | ፭ | |||
| бенгальский | ৫ | |||
| каннада | ೫ | |||
| пенджаби | ੫ | |||
| китайские цифры | 五 | |||
| армянский | Ե | |||
| Деванагари | ५ | |||
| иврит | ה | |||
| кхмерский | ៥ | |||
| телугу | ౫ | |||
| малаялам | ൫ | |||
| тамильский | ௫ | |||
| тайский | к | |||
| Вавилонское число | 𒐙 | |||
| Египетский иероглиф , китайский счетный стержень | ||||| | |||
| Цифры майя | 𝋥 | |||
| азбука Морзе | ..... | |||
| ASCII-значение | ENQ | |||
5 ( пять ) — число , цифра и числовое значение . Это натуральное число , количественное числительное , следующее за 4 и предшествующее 6 , и является простым числом .
У людей и многих других животных на конечностях по 5 пальцев .
Математика

5 — простое число Ферма , показатель степени простого числа Мерсенна , а также число Фибоначчи . 5 — первое конгруэнтное число , а также длина гипотенузы наименьшего прямоугольного треугольника с целыми сторонами , входящего в наименьшую пифагорейскую тройку ( 3 , 4 , 5). [1]
5 — первое безопасное простое число [2] и первое хорошее простое число . [3] 11 образует первую пару сексуальных простых чисел с 5. [4] 5 — второе простое число Ферма из пяти известных простых чисел Ферма. [5] 5 также является первым из трех известных простых чисел Вильсона (5, 13, 563). [6]
Геометрия
Фигура с пятью сторонами называется пентагон . Пентагон — первый правильный многоугольник , который не замощает плоскость своими копиями. Это самая большая грань, которую может иметь любое из пяти правильных трехмерных правильных Платоновых тел .
Коника определяется с помощью пяти точек таким же образом, как для определения прямой нужны две точки . [7] Пентаграмма , или пятиконечная полиграмма , представляет собой звездчатый многоугольник, построенный путем соединения некоторых несмежных частей правильного пятиугольника в качестве самопересекающихся ребер . [8] Внутренняя геометрия пятиугольника и пентаграммы (представленная символом Шлефли {5/2} ) занимает видное место в мозаиках Пенроуза . Пентаграммы представляют собой грани внутри звездчатых многогранников Кеплера–Пуансо и звездчатых многогранников Шлефли–Гесса .
Существует пять правильных Платоновых тел: тетраэдр , куб , октаэдр , додекаэдр и икосаэдр . [ 9]
Хроматическое число плоскости — это минимальное количество цветов, необходимое для раскрашивания плоскости таким образом, чтобы ни одна пара точек на расстоянии 1 не имела одинаковый цвет. [ 10] Пять — это меньшее число, зависящее от хроматического числа плоскости, но это может зависеть от выбора аксиом теории множеств : [11]
Плоскость содержит в общей сложности пять решеток Браве , или массивов точек, определяемых дискретными операциями переноса . Однородные мозаики плоскости генерируются из комбинаций всего пяти правильных многоугольников. [12]
Геометрия более высокого измерения
Гипертетраэдр , или 5-ячейка, является 4- мерным аналогом тетраэдра . Он имеет пять вершин. Его ортографическая проекция гомоморфна группе K 5. [ 13] : стр.120
Существует пять фундаментальных семейств точечных групп зеркальной симметрии в 4-мерном пространстве . Существует также 5 компактных гиперболических групп Коксетера , или 4-призм , ранга 5, каждая из которых генерирует однородные соты в гиперболическом 4-пространстве как перестановки колец диаграмм Коксетера. [14]

Алгебра
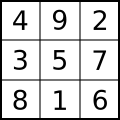
5 — значение центральной ячейки первого нетривиального нормального магического квадрата , называемого квадратом Луошу . Все целые числа можно выразить как сумму пяти ненулевых квадратов . [15] [16] Существует пять счетно бесконечных классов Рамсея перестановок . [ 17] : с.4 Предполагается , что 5 — единственное нечетное , неприкасаемое число ; если это так, то пять будет единственным нечетным простым числом, которое не является основанием аликвотного дерева. [18]

 ).
).Предполагается, что каждое нечетное число больше пяти может быть выражено как сумма трех простых чисел; Хельфготт предоставил доказательство этого [19] (также известное как нечетная гипотеза Гольдбаха ), которое уже широко признано математиками, поскольку оно все еще проходит экспертную оценку . С другой стороны, каждое нечетное число больше единицы является суммой не более пяти простых чисел (как нижний предел). [20]
Теория групп
В теории графов все графы с четырьмя или менее вершинами являются планарными , однако существует граф с пятью вершинами, который не является: K 5 , полный граф с пятью вершинами. По теореме Куратовского , конечный граф является планарным тогда и только тогда, когда он не содержит подграфа, который является подразделением , или K 3,3 , графа полезности . [21]
Существует пять комплексных исключительных алгебр Ли . Пять групп Матье составляют первое поколение в счастливом семействе спорадических групп . Это также первые пять спорадических групп, которые были описаны . [22] : стр.54 Централизатор элемента порядка 5 внутри наибольшей спорадической группы возникает из произведения спорадической группы Харады–Нортона и группы порядка 5. [23] [24]
Список основных расчетов
| Умножение | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 × х | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| Разделение | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 ÷ х | 5 | 2.5 | 1. 6 | 1.25 | 1 | 0,8 3 | 0.714285 | 0,625 | 0. 5 | 0,5 | 0. 45 | 0,41 6 | 0.384615 | 0.3 571428 | 0. 3 |
| х ÷ 5 | 0.2 | 0,4 | 0,6 | 0.8 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.4 | 2.6 | 2.8 | 3 |
| Возведение в степень | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 х | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 | 48828125 | 244140625 | 1220703125 | 6103515625 | 30517578125 |
| х 5 | 1 | 32 | 243 | 1024 | 7776 | 16807 | 32768 | 59049 | 100000 | 161051 | 248832 | 371293 | 537824 | 759375 |
Эволюция арабской цифры

Эволюция современной западной цифры для обозначения цифры пять восходит к индийской системе цифр, где в некоторых ранних версиях цифра имела сходство с вариациями цифры четыре, а не с «5» (как она представлена сегодня). Империи Кушана и Гупта на территории современной Индии имели между собой несколько форм, которые не имели никакого сходства с современной цифрой. Позже арабские традиции преобразовали цифру несколькими способами, создав формы, которые все еще были похожи на цифру четыре, со сходством с цифрой три; но все еще непохожи на современную пять. [25] Именно из этих цифр европейцы в конечном итоге придумали современную 5 (представленную, например, в трудах Дюрера).
В то время как в большинстве современных шрифтов форма символа цифры 5 имеет выносной элемент , в шрифтах с текстовыми цифрами глиф обычно имеет подстрочный элемент , как, например, в .
.

На семисегментном дисплее калькулятора и цифровых часов он часто представлен пятью сегментами в четырех последовательных поворотах сверху вниз, вращаясь сначала против часовой стрелки, затем по часовой стрелке и наоборот. Это одно из трех чисел, наряду с 4 и 6, где количество сегментов соответствует числу. Это делает его часто неотличимым от буквы S. Дисплеи с большим количеством сегментов иногда могут использовать диагональ для одного из двух.
Другие поля
Религия
ислам
Пять столпов ислама . [26] Пятиконечная простая звезда ☆ — одна из пяти, используемых в исламских плитках гирих . [27]
Мистика
Гностицизм
Число пять было важным символическим числом в манихействе , где небесные существа, концепции и другие часто группировались в группы по пять. [ необходима цитата ]
Пентаграмма , или пятиконечная звезда, имеет мистическое значение в различных системах верований, включая бахаи , христианство , масонство , сатанизм , даосизм , телему и викку .
Разнообразный

- «Дай мне пять» — это распространенная фраза, используемая перед приветствием «дай пять» .
Смотрите также
Ссылки
- ^ Sloane, N. J. A. (ред.). "Последовательность A003273 (Конгруэнтные числа)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 01.06.2016 .
- ^ Sloane, N. J. A. (ред.). "Последовательность A005385 (Безопасные простые числа p: (p-1)/2 также являются простыми числами)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 14.02.2023 .
- ^ Sloane, N. J. A. (ред.). "Последовательность A028388 (хорошие простые числа)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 01.06.2016 .
- ^ Sloane, N. J. A. (ред.). "Последовательность A023201 (Простые числа p, такие, что p + 6 также является простым числом. (Меньшее из пары сексуальных простых чисел.))". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 14.01.2023 .
- ^ Sloane, N. J. A. (ред.). "Последовательность A019434 (простые числа Ферма)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 21 июля 2022 г.
- ^ Sloane, N. J. A. (ред.). "Последовательность A007540 (простые числа Уилсона: простые числа p, такие, что (p-1)! равно -1 (mod p^2).)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 06.09.2023 .
- ^ Диксон, AC (март 1908 г.). «Коническое сечение через пять данных точек». The Mathematical Gazette . 4 (70). The Mathematical Association: 228– 230. doi :10.2307/3605147. JSTOR 3605147. S2CID 125356690.
- ^ Слоан, Н. Дж. А. (ред.). «Последовательность A307681 (Разница между числом сторон и числом диагоналей выпуклого n-угольника.)». Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.
- ↑ Брайан Банч, Королевство бесконечных чисел . Нью-Йорк: WH Freeman & Company (2000): 61
- ^ de Grey, Aubrey DNJ (2018). «Хроматическое число плоскости не менее 5». Geombinatorics . 28 : 5–18 . arXiv : 1804.02385 . MR 3820926. S2CID 119273214.
- ^ Exoo, Geoffrey; Ismailescu, Dan (2020). «Хроматическое число плоскости не менее 5: новое доказательство». Дискретная и вычислительная геометрия . 64. Нью-Йорк, Нью-Йорк: Springer : 216– 226. arXiv : 1805.00157 . doi : 10.1007/s00454-019-00058-1. MR 4110534. S2CID 119266055. Zbl 1445.05040.
- ^ Грюнбаум, Бранко ; Шепард, Джеффри (ноябрь 1977 г.). "Tilings by Regular Polygons" (PDF) . Mathematics Magazine . 50 (5). Taylor & Francis, Ltd.: 227– 236. doi :10.2307/2689529. JSTOR 2689529. S2CID 123776612. Zbl 0385.51006. Архивировано из оригинала (PDF) 2016-03-03 . Получено 2023-01-18 .
- ^ HSM Coxeter (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Dover Publications, Inc. стр. 1–368 . ISBN 978-0-486-61480-9.
- ^ МакМаллен, Питер ; Шульте, Эгон (2002). Абстрактные правильные многогранники . Энциклопедия математики и ее приложений. Т. 92. Кембридж: Cambridge University Press. С. 162– 164. doi :10.1017/CBO9780511546686. ISBN 0-521-81496-0. MR 1965665. S2CID 115688843.
- ^ Нивен, Иван ; Цукерман, Герберт С.; Монтгомери, Хью Л. (1980). Введение в теорию чисел (5-е изд.). Нью-Йорк, Нью-Йорк: John Wiley . С. 144, 145. ISBN 978-0-19-853171-5.
- ^ Sloane, N. J. A. (ред.). "Последовательность A047701 (Все положительные числа, которые не являются суммой 5 ненулевых квадратов.)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 2023-09-20 .
- Только двенадцать целых чисел до 33 не могут быть выражены в виде суммы пяти ненулевых квадратов: {1, 2, 3, 4, 6, 7, 9, 10, 12, 15, 18, 33}, где 2, 3 и 7 — единственные такие простые числа без выражения.
- ^ Бёттхер, Джулия ; Фониок, Ян (2013). «Свойства Рамсея перестановок». Электронный журнал комбинаторики . 20 (1): P2. arXiv : 1103.5686v2 . doi : 10.37236/2978. S2CID 17184541. Zbl 1267.05284.
- ^ Померанс, Карл; Ян, Хи-Сун (14 июня 2012 г.). «О неприкасаемых числах и связанных с ними проблемах» (PDF) . math.dartmouth.edu . Дартмутский колледж : 1. S2CID 30344483.Классификация предметов по математике 2010 года. 11A25, 11Y70, 11Y16.
- ^ Хельфготт, Харальд Андрес (2014). «Тернарная проблема Гольдбаха» (PDF) . Ин Джанг, Сан Ён (ред.). Труды Сеульского международного конгресса математиков . Том 2. Сеул, Корея: Kyung Moon SA. стр. 391–418 . ISBN 978-89-6105-805-6. OCLC 913564239.
- ^ Тао, Теренс (март 2014 г.). «Каждое нечетное число, большее 1, имеет представление в виде суммы не более пяти простых чисел» (PDF) . Mathematics of Computation . 83 (286): 997– 1038. doi :10.1090/S0025-5718-2013-02733-0. MR 3143702. S2CID 2618958.
- ^ Бернстайн, Майкл (1978). «Теорема Куратовского-Понтрягина о планарных графах». Журнал комбинаторной теории . Серия B. 24 (2): 228– 232. doi : 10.1016/0095-8956(78)90024-2 .
- ^ Роберт Л. Грисс-младший (1998). Двенадцать спорадических групп . Монографии Спрингера по математике. Берлин: Springer-Verlag. стр. 1−169. дои : 10.1007/978-3-662-03516-0. ISBN 978-3-540-62778-4. МР 1707296. S2CID 116914446. Збл 0908.20007.
- ^ Люкс, Клаус; Ноеске, Феликс; Рыба, Александр JE (2008). «5-модулярные характеры спорадической простой группы Харады–Нортона HN и ее группа автоморфизмов HN.2». Журнал алгебры . 319 (1). Амстердам: Elsevier : 320–335 . doi : 10.1016/j.jalgebra.2007.03.046 . MR 2378074. S2CID 120706746. Zbl 1135.20007.
- ^ Уилсон, Роберт А. (2009). «Нечетные локальные подгруппы монстра». Журнал Австралийского математического общества (серия A) . 44 (1). Кембридж: Cambridge University Press : 12– 13. doi : 10.1017/S1446788700031323 . MR 0914399. S2CID 123184319. Zbl 0636.20014.
- ^ Жорж Ифра, Всеобщая история чисел: от доисторических времен до изобретения компьютера , перевод Дэвида Беллоса и др. Лондон: The Harvill Press (1998): 394, рис. 24.65
- ^ "PBS – Ислам: Империя веры – Вера – Пять столпов". www.pbs.org . Получено 2020-08-03 .
- ^ Сарханги, Реза (2012). «Взаимодействующие звездчатые многоугольники в персидской архитектуре: особый случай декаграммы в мозаичных узорах» (PDF) . Nexus Network Journal . 14 (2): 350. doi : 10.1007/s00004-012-0117-5 . S2CID 124558613.
Дальнейшее чтение
- Уэллс, Д. (1987). Словарь любопытных и интересных чисел издательства Penguin . Лондон, Великобритания: Penguin Group . С. 58–67 .




