Математическая физика
| Часть серии статей о | ||
| Математика | ||
|---|---|---|
 Математический портал Математический портал | ||
| Часть серии статей о |
| Физика |
|---|
 |
|

Математическая физика относится к разработке математических методов для применения к проблемам в физике . Журнал математической физики определяет эту область как «применение математики к проблемам в физике и разработку математических методов, подходящих для таких приложений и для формулирования физических теорий». [1] Альтернативное определение также включало бы те области математики, которые вдохновлены физикой, известные как физическая математика . [2]
Объем
Существует несколько отдельных разделов математической физики, и они примерно соответствуют определенным историческим частям нашего мира.
Классическая механика
Применение методов математической физики к классической механике обычно включает в себя строгую, абстрактную и продвинутую переформулировку ньютоновской механики в терминах лагранжевой механики и гамильтоновой механики (включая оба подхода при наличии ограничений). Обе формулировки воплощены в аналитической механике и приводят к пониманию глубокого взаимодействия между понятиями симметрии и сохраняющимися величинами в ходе динамической эволюции механических систем, как это воплощено в самой элементарной формулировке теоремы Нётер . Эти подходы и идеи были распространены на другие области физики, такие как статистическая механика , механика сплошной среды , классическая теория поля и квантовая теория поля . Более того, они предоставили множество примеров и идей в дифференциальной геометрии (например, несколько понятий в симплектической геометрии и векторных расслоениях ).
Уравнения с частными производными
В рамках собственно математики теория дифференциальных уравнений с частными производными , вариационное исчисление , анализ Фурье , теория потенциала и векторный анализ , пожалуй, наиболее тесно связаны с математической физикой. Эти области интенсивно развивались со второй половины XVIII века (например, Д'Аламбером , Эйлером и Лагранжем ) до 1930-х годов. Физические приложения этих разработок включают гидродинамику , небесную механику , механику сплошных сред , теорию упругости , акустику , термодинамику , электричество , магнетизм и аэродинамику .
Квантовая теория
Теория атомных спектров (а позднее и квантовая механика ) развивалась почти одновременно с некоторыми разделами математической области линейной алгебры , спектральной теории операторов , операторных алгебр и, в более широком смысле, функционального анализа . Нерелятивистская квантовая механика включает операторы Шредингера и имеет связи с атомной и молекулярной физикой . Квантовая теория информации — еще одна узкая специальность.
Теория относительности и квантово-релятивистские теории
Специальные и общие теории относительности требуют совершенно иного типа математики. Это была теория групп , которая играла важную роль как в квантовой теории поля, так и в дифференциальной геометрии . Однако она постепенно дополнялась топологией и функциональным анализом в математическом описании космологических , а также квантово-полевых явлений. В математическом описании этих физических областей также важны некоторые концепции гомологической алгебры и теории категорий [3] .
Статистическая механика
Статистическая механика образует отдельную область, которая включает теорию фазовых переходов . Она опирается на гамильтонову механику (или ее квантовую версию) и тесно связана с более математической эргодической теорией и некоторыми частями теории вероятностей . Растет взаимодействие между комбинаторикой и физикой , в частности, статистической физикой.
Использование
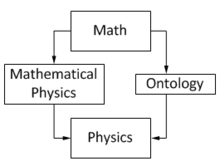
Использование термина «математическая физика» иногда является своеобразным . Некоторые части математики, которые изначально возникли в результате развития физики , на самом деле не считаются частями математической физики, в то время как другие тесно связанные области считаются. Например, обыкновенные дифференциальные уравнения и симплектическая геометрия обычно рассматриваются как чисто математические дисциплины, тогда как динамические системы и гамильтонова механика относятся к математической физике. Джон Херапат использовал этот термин для названия своего текста 1847 года о «математических принципах натуральной философии», сферой действия которого в то время были «причины тепла, газообразной упругости, гравитации и других великих явлений природы». [4]
Математическая и теоретическая физика
Термин «математическая физика» иногда используется для обозначения исследований, направленных на изучение и решение проблем в физике или мысленных экспериментов в математически строгой структуре. В этом смысле математическая физика охватывает очень широкую академическую область, отличающуюся только смешением некоторого математического аспекта и аспекта теоретической физики. Хотя математическая физика связана с теоретической физикой , [5] в этом смысле она подчеркивает математическую строгость аналогичного типа, как в математике.
С другой стороны, теоретическая физика подчеркивает связи с наблюдениями и экспериментальной физикой , что часто требует от физиков-теоретиков (и физиков-математиков в более общем смысле) использования эвристических , интуитивных или приблизительных аргументов. [6] Такие аргументы не считаются математиками строгими.
Такие математические физики в первую очередь расширяют и проясняют физические теории . Из-за требуемого уровня математической строгости эти исследователи часто имеют дело с вопросами, которые физики-теоретики считали уже решенными. Однако иногда они могут показать, что предыдущее решение было неполным, неверным или просто слишком наивным. Примерами являются вопросы о попытках вывести второй закон термодинамики из статистической механики . [ необходима цитата ] Другие примеры касаются тонкостей, связанных с процедурами синхронизации в специальной и общей теории относительности ( эффект Саньяка и синхронизация Эйнштейна ).
Попытка поставить физические теории на математически строгую основу не только развила физику, но и повлияла на развитие некоторых математических областей. Например, развитие квантовой механики и некоторых аспектов функционального анализа во многом параллельны друг другу. Математическое изучение квантовой механики , квантовой теории поля и квантовой статистической механики мотивировало результаты в операторных алгебрах . Попытка построить строгую математическую формулировку квантовой теории поля также привела к некоторому прогрессу в таких областях, как теория представлений .
Выдающиеся физики-математики
До Ньютона
Существует традиция математического анализа природы, которая восходит к древним грекам; примерами являются Евклид ( Оптика ), Архимед ( О равновесии плоскостей , О плавающих телах ) и Птолемей ( Оптика , Гармоника ). [7] [8] Позднее исламские и византийские ученые развивали эти работы, и в конечном итоге они были вновь введены или стали доступны Западу в XII веке и в эпоху Возрождения .
В первом десятилетии XVI века любитель астрономии Николай Коперник предложил гелиоцентризм и опубликовал трактат о нем в 1543 году. Он сохранил идею Птолемея об эпициклах и просто стремился упростить астрономию, построив более простые наборы эпициклических орбит. Эпициклы состоят из окружностей на окружностях. Согласно аристотелевской физике , окружность была совершенной формой движения и была внутренним движением пятого элемента Аристотеля — квинтэссенции или универсальной сущности, известной по-гречески как эфир для английского чистого воздуха — который был чистой субстанцией за пределами подлунной сферы , и, таким образом, был чистым составом небесных сущностей. Немец Иоганн Кеплер [1571–1630], помощник Тихо Браге , модифицировал коперниканские орбиты в эллипсы , формализованные в уравнениях законов Кеплера о движении планет .
Увлеченный атомист Галилео Галилей в своей книге 1623 года «Пробирщик» утверждал, что «книга природы написана математикой». [9] Его книга 1632 года о его телескопических наблюдениях поддерживала гелиоцентризм. [10] Введя эксперимент, Галилей затем опроверг геоцентрическую космологию , опровергнув саму физику Аристотеля. Книга Галилея 1638 года «Рассуждение о двух новых науках» установила закон равного свободного падения, а также принципы инерционного движения, положив начало центральным концепциям того, что станет сегодняшней классической механикой . [10] Согласно закону инерции Галилея , а также принципу инвариантности Галилея , также называемому относительностью Галилея, для любого объекта, испытывающего инерцию, существует эмпирическое обоснование знания только того, что он находится в относительном покое или относительном движении — покое или движении по отношению к другому объекту.
Рене Декарт разработал полную систему гелиоцентрической космологии, основанную на принципе вихревого движения, декартовой физике , широкое признание которой помогло привести к краху аристотелевскую физику. Декарт использовал математическое обоснование в качестве модели для науки и разработал аналитическую геометрию , которая со временем позволила наносить на карту местоположения в трехмерном пространстве ( декартовы координаты ) и отмечать их прогрессии по потоку времени. [11]
Христиан Гюйгенс , талантливый математик и физик, старший современник Ньютона, был первым, кто успешно идеализировал физическую проблему с помощью набора параметров в своем труде Horologium Oscillatorum (1673), и первым, кто полностью математизировал механистическое объяснение ненаблюдаемого физического явления в Traité de la Lumière (1690). По этим причинам он считается первым физиком-теоретиком и одним из основателей современной математической физики. [12] [13]
Ньютоновская физика и пост-ньютоновская
Преобладающая структура науки в XVI и начале XVII веков была заимствована из древнегреческой математики , где геометрические формы формировали строительные блоки для описания и размышления о пространстве, а время часто мыслилось как отдельная сущность. С введением алгебры в геометрию, а вместе с ней и идеи системы координат, время и пространство теперь могли быть осями, принадлежащими одной плоскости. Эта существенная математическая структура лежит в основе всей современной физики и используется во всех дальнейших математических структурах, разработанных в последующие столетия.
К середине XVII века такие важные концепции, как фундаментальная теорема исчисления (доказанная в 1668 году шотландским математиком Джеймсом Грегори ) и нахождение экстремумов и минимумов функций с помощью дифференцирования с использованием теоремы Ферма (французским математиком Пьером де Ферма ), были известны уже до Лейбница и Ньютона. [14] Исаак Ньютон (1642–1727) разработал исчисление (хотя Готфрид Вильгельм Лейбниц разработал схожие концепции вне контекста физики) и метод Ньютона для решения задач в математике и физике. Он был чрезвычайно успешен в своем применении исчисления и других методов к изучению движения. Теория движения Ньютона, достигшая кульминации в его Philosophiæ Naturalis Principia Mathematica ( Математические начала натуральной философии ) в 1687 году, смоделировала три закона движения Галилея вместе с законом всемирного тяготения Ньютона в рамках абсолютного пространства — гипотетически выдвинутого Ньютоном как физически реальная сущность евклидовой геометрической структуры, простирающейся бесконечно во всех направлениях — при этом предполагая абсолютное время , предположительно оправдывая знание абсолютного движения, движения объекта относительно абсолютного пространства. [15] Принцип инвариантности/относительности Галилея был просто подразумеваемым в теории движения Ньютона. Якобы сведя небесные законы движения Кеплера, а также земные законы движения Галилея к объединяющей силе, Ньютон достиг большой математической строгости, но с теоретической небрежностью. [16]
В 18 веке швейцарец Даниил Бернулли (1700–1782) внес вклад в гидродинамику и вибрирующие струны . Швейцарец Леонард Эйлер (1707–1783) провел особую работу в вариационном исчислении , динамике, гидродинамике и других областях. Также был известен француз итальянского происхождения Жозеф-Луи Лагранж (1736–1813) за работу в области аналитической механики : он сформулировал механику Лагранжа и вариационные методы. Большой вклад в формулировку аналитической динамики, называемой гамильтоновой динамикой, также внес ирландский физик, астроном и математик Уильям Роуэн Гамильтон (1805–1865). Гамильтонова динамика сыграла важную роль в формулировке современных теорий в физике, включая теорию поля и квантовую механику. Французский физик и математик Жозеф Фурье (1768–1830) ввел понятие рядов Фурье для решения уравнения теплопроводности , что дало начало новому подходу к решению уравнений в частных производных с помощью интегральных преобразований .
В начале 19 века математики из Франции, Германии и Англии внесли свой вклад в математическую физику. Француз Пьер-Симон Лаплас (1749–1827) внес важнейший вклад в математическую астрономию , теорию потенциала . Симеон Дени Пуассон (1781–1840) работал в области аналитической механики и теории потенциала . В Германии Карл Фридрих Гаусс (1777–1855) внес ключевой вклад в теоретические основы электричества , магнетизма , механики и гидродинамики . В Англии Джордж Грин (1793–1841) опубликовал в 1828 году «Очерк о применении математического анализа к теориям электричества и магнетизма» , который в дополнение к своему значительному вкладу в математику сделал ранний прогресс в направлении установления математических основ электричества и магнетизма.
За пару десятилетий до публикации Ньютоном корпускулярной теории света голландец Христиан Гюйгенс (1629–1695) разработал волновую теорию света, опубликованную в 1690 году. К 1804 году эксперимент Томаса Юнга с двумя щелями выявил интерференционную картину, как будто свет был волной, и, таким образом, волновая теория света Гюйгенса, а также вывод Гюйгенса о том, что световые волны являются колебаниями светоносного эфира , были приняты. Жан-Огюстен Френель смоделировал гипотетическое поведение эфира. Английский физик Майкл Фарадей ввел теоретическую концепцию поля, а не действия на расстоянии. В середине 19 века шотландец Джеймс Клерк Максвелл (1831–1879) свел электричество и магнетизм к теории электромагнитного поля Максвелла, сокращенной другими до четырех уравнений Максвелла . Первоначально оптика была обнаружена как следствие [ необходимо уточнение ] поля Максвелла. Позже излучение, а затем и известный сегодня электромагнитный спектр были обнаружены также как следствие [ необходимо уточнение ] этого электромагнитного поля.
Английский физик лорд Рэлей [1842–1919] работал над звуком . Ирландцы Уильям Роуэн Гамильтон (1805–1865), Джордж Габриэль Стокс (1819–1903) и лорд Кельвин (1824–1907) создали несколько крупных работ: Стокс был лидером в оптике и гидродинамике; Кельвин сделал существенные открытия в термодинамике ; Гамильтон проделал заметную работу по аналитической механике , открыв новый и мощный подход, ныне известный как гамильтонова механика . Весьма существенный вклад в этот подход был сделан его немецким коллегой математиком Карлом Густавом Якоби (1804–1851), в частности, ссылаясь на канонические преобразования . Немец Герман фон Гельмгольц (1821–1894) внес существенный вклад в области электромагнетизма , волн, жидкостей и звука. В Соединенных Штатах новаторская работа Джозайи Уилларда Гиббса (1839–1903) стала основой статистической механики . Фундаментальные теоретические результаты в этой области были достигнуты немцем Людвигом Больцманом (1844–1906). Вместе эти люди заложили основы электромагнитной теории, гидродинамики и статистической механики.
Релятивистский
К 1880-м годам появился заметный парадокс, что наблюдатель в электромагнитном поле Максвелла измерял его с приблизительно постоянной скоростью, независимо от скорости наблюдателя относительно других объектов в электромагнитном поле. Таким образом, хотя скорость наблюдателя постоянно терялась [ необходимо разъяснение ] относительно электромагнитного поля, она сохранялась относительно других объектов в электромагнитном поле. И все же не было обнаружено никакого нарушения инвариантности Галилея в физических взаимодействиях между объектами. Поскольку электромагнитное поле Максвелла было смоделировано как колебания эфира , физики сделали вывод, что движение в эфире приводит к дрейфу эфира, смещающему электромагнитное поле, объясняя недостающую скорость наблюдателя относительно него. Преобразование Галилея было математическим процессом, используемым для перевода положений в одной системе отсчета в предсказания положений в другой системе отсчета, все построенные в декартовых координатах , но этот процесс был заменен преобразованием Лоренца , смоделированным голландцем Хендриком Лоренцом [1853–1928].
Однако в 1887 году экспериментаторы Майкельсон и Морли не смогли обнаружить эфирный дрейф. Была выдвинута гипотеза, что движение в эфир также вызвало сокращение эфира, как это было смоделировано в сокращении Лоренца . Была выдвинута гипотеза, что эфир таким образом поддерживал электромагнитное поле Максвелла в соответствии с принципом инвариантности Галилея во всех инерциальных системах отсчета , в то время как теория движения Ньютона была сохранена.
Австрийский физик-теоретик и философ Эрнст Мах критиковал постулированное Ньютоном абсолютное пространство. Математик Жюль-Анри Пуанкаре (1854–1912) подвергал сомнению даже абсолютное время. В 1905 году Пьер Дюгем опубликовал сокрушительную критику основ теории движения Ньютона. [16] Также в 1905 году Альберт Эйнштейн (1879–1955) опубликовал свою специальную теорию относительности , по-новому объяснив как инвариантность электромагнитного поля, так и галилеевскую инвариантность, отбросив все гипотезы, касающиеся эфира, включая существование самого эфира. Опровергая основу теории Ньютона — абсолютное пространство и абсолютное время — специальная теория относительности относится к относительному пространству и относительному времени , в результате чего длина сокращается, а время расширяется вдоль пути движения объекта.
Декартовы координаты произвольно использовали прямолинейные координаты. Гаусс, вдохновленный работой Декарта, ввел искривленную геометрию, заменив прямолинейные оси искривленными. Гаусс также ввел еще один ключевой инструмент современной физики — кривизну. Работа Гаусса была ограничена двумя измерениями. Расширение ее до трех или более измерений внесло большую сложность, с необходимостью (еще не изобретенных) тензоров. Именно Римман был тем, кто отвечал за расширение искривленной геометрии до N измерений. В 1908 году бывший профессор математики Эйнштейна Герман Минковский применил конструкцию искривленной геометрии для моделирования трехмерного пространства вместе с одномерной осью времени, рассматривая временную ось как четвертое пространственное измерение — в целом 4D пространство-время — и объявил о неизбежной кончине разделения пространства и времени. [17] Эйнштейн изначально называл это «излишней ученостью», но позже использовал пространство-время Минковского с большой элегантностью в своей общей теории относительности , [18] распространив инвариантность на все системы отсчета — воспринимаемые как инерциальные или как ускоренные — и приписал это Минковскому, к тому времени покойному. Общая теория относительности заменяет декартовы координаты на гауссовы координаты и заменяет заявленное Ньютоном пустое, но евклидово пространство, мгновенно пересекаемое вектором гипотетической гравитационной силы Ньютона — мгновенное действие на расстоянии — гравитационным полем . Гравитационное поле — это само пространство-время Минковского , 4D- топология эфира Эйнштейна, смоделированная на лоренцевом многообразии , которое «искривляется» геометрически, согласно тензору кривизны Римана . Концепция гравитации Ньютона: «две массы притягиваются друг к другу» заменена геометрическим аргументом: «масса преобразует кривизну пространства-времени , а свободно падающие частицы с массой движутся по геодезической кривой в пространстве-времени» ( Риманова геометрия существовала еще до 1850-х годов математиками Карлом Фридрихом Гауссом и Бернхардом Риманом в поисках внутренней геометрии и неевклидовой геометрии), вблизи либо массы, либо энергии. (В специальной теории относительности — частном случае общей теории относительности — даже безмассовая энергия оказывает гравитационное воздействие за счет своей эквивалентности массе, локально «искривляя» геометрию четырех единых измерений пространства и времени.)
Квантовый
Другим революционным достижением 20-го века стала квантовая теория , которая возникла из основополагающих трудов Макса Планка (1856–1947) (об излучении черного тела ) и работы Эйнштейна по фотоэлектрическому эффекту . В 1912 году математик Анри Пуанкаре опубликовал работу Sur la théorie des quanta . [19] [20] В этой статье он ввел первое ненаивное определение квантования. Развитие ранней квантовой физики сопровождалось эвристической структурой, разработанной Арнольдом Зоммерфельдом (1868–1951) и Нильсом Бором (1885–1962), но вскоре ее заменила квантовая механика, разработанная Максом Борном (1882–1970), Луи де Бройлем (1892–1987), Вернером Гейзенбергом (1901–1976), Полем Дираком (1902–1984), Эрвином Шредингером (1887–1961), Сатьендра Натом Бозе (1894–1974) и Вольфгангом Паули (1900–1958). Эта революционная теоретическая структура основана на вероятностной интерпретации состояний, эволюции и измерений в терминах самосопряженных операторов на бесконечномерном векторном пространстве. Это называется гильбертовым пространством (введено математиками Давидом Гильбертом (1862–1943), Эрхардом Шмидтом (1876–1959) и Фридьешем Риссом (1880–1956) в поисках обобщения евклидова пространства и изучения интегральных уравнений), и строго определено в аксиоматической современной версии Джоном фон Нейманом в его знаменитой книге « Математические основы квантовой механики» , где он построил важную часть современного функционального анализа на гильбертовых пространствах, спектральную теорию (введенную Давидом Гильбертом , который исследовал квадратичные формы с бесконечным числом переменных. Много лет спустя было обнаружено, что его спектральная теория связана со спектром атома водорода. Он был удивлен этим применением.) в частности. Поль Дирак использовал алгебраические конструкции для создания релятивистской модели для электрона , предсказывая его магнитный момент и существование его античастицы, позитрона .
Список выдающихся деятелей математической физики в 20 веке
Выдающиеся деятели математической физики XX века (перечислены по дате рождения):
- Уильям Томсон (лорд Кельвин) (1824–1907)
- Оливер Хевисайд (1850–1925)
- Жюль Анри Пуанкаре (1854–1912)
- Давид Гильберт (1862–1943)
- Арнольд Зоммерфельд (1868–1951)
- Константин Каратеодори (1873–1950)
- Альберт Эйнштейн (1879–1955)
- Эмми Нётер (1882–1935)
- Макс Борн (1882–1970)
- Джордж Дэвид Биркгоф (1884–1944)
- Герман Вайль (1885–1955)
- Сатьендра Натх Бос (1894–1974)
- Луи де Бройль (1892–1987)
- Норберт Винер (1894–1964)
- Джон Лайтон Синг (1897–1995)
- Марио Шенберг (1914–1990)
- Вольфганг Паули (1900–1958)
- Поль Дирак (1902–1984)
- Юджин Вигнер (1902–1995)
- Андрей Колмогоров (1903–1987)
- Ларс Онсагер (1903–1976)
- Джон фон Нейман (1903–1957)
- Син-Итиро Томонага (1906–1979)
- Хидеки Юкава (1907–1981)
- Николай Николаевич Боголюбов (1909–1992).
- Субраманьян Чандрасекхар (1910–1995)
- Марк Кац (1914–1984)
- Джулиан Швингер (1918–1994)
- Ричард Филлипс Фейнман (1918–1988)
- Ирвинг Эзра Сигал (1918–1998)
- Рёго Кубо (1920–1995)
- Артур Стронг Уайтман (1922–2013)
- Чэнь-Нин Ян (1922–)
- Рудольф Хааг (1922–2016)
- Фримен Джон Дайсон (1923–2020)
- Мартин Гуцвиллер (1925–2014)
- Абдус Салам (1926–1996)
- Юрген Мозер (1928–1999)
- Майкл Фрэнсис Атья (1929–2019)
- Джоэл Луис Лебовиц (1930–)
- Роджер Пенроуз (1931–)
- Эллиотт Гершель Либ (1932–)
- Якир Ахаронов (1932–)
- Шелдон Глэшоу (1932–)
- Стивен Вайнберг (1933–2021)
- Людвиг Дмитриевич Фаддеев (1934–2017).
- Дэвид Рюэль (1935–)
- Яков Григорьевич Синай (1935–)
- Владимир Игоревич Арнольд (1937–2010)
- Артур Майкл Джаффе (1937–)
- Роман Владимир Яцкив (1939–)
- Леонард Сасскинд (1940–)
- Родни Джеймс Бакстер (1940–)
- Майкл Виктор Берри (1941–)
- Джованни Галлавотти (1941–)
- Стивен Уильям Хокинг (1942–2018)
- Джерролд Элдон Марсден (1942–2010)
- Майкл С. Рид (1942–)
- Джон Майкл Костерлиц (1943–)
- Исраэль Майкл Сигал (1945–)
- Александр Маркович Поляков (1945–)
- Барри Саймон (1946–)
- Герберт Спон (1946–)
- Джон Лоуренс Карди (1947–)
- Джорджио Паризи (1948-)
- Абхай Аштекар (1949-)
- Эдвард Виттен (1951–)
- Ф. Дункан Холдейн (1951–)
- Ашоке Сен (1956–)
- Хуан Мартин Мальдасена (1968–)
Смотрите также
- Международная ассоциация математической физики
- Известные публикации по математической физике
- Список журналов по математической физике
- Калибровочная теория (математика)
- Связь между математикой и физикой
- Теоретическая , вычислительная и философская физика
Примечания
- ^ Определение из журнала математической физики . "Архивная копия". Архивировано из оригинала 2006-10-03 . Получено 2006-10-03 .
{{cite web}}: CS1 maint: archived copy as title (link) - ^ "Физическая математика и будущее" (PDF) . www.physics.rutgers.edu . Получено 2022-05-09 .
- ^ "квантовая теория поля". nLab .
- ^ Джон Херапат (1847) Математическая физика, или Математические начала натуральной философии, причины тепла, упругости газов, гравитации и других великих явлений природы, Уиттекер и компания через HathiTrust
- ^ Цитата: "...отрицательное определение теоретика указывает на его неспособность проводить физические эксперименты, тогда как положительное... подразумевает его энциклопедические познания в физике в сочетании с обладанием достаточной математической вооруженностью. В зависимости от соотношения этих двух компонентов теоретик может быть ближе либо к экспериментатору, либо к математику. В последнем случае его обычно считают специалистом по математической физике.", Я. Френкель, как указано в А. Т. Филиппов, Универсальный солитон , стр. 131. Биркхаузер, 2000.
- ↑ Цитата: «Физическая теория — это нечто вроде костюма, сшитого для Природы. Хорошая теория — как хороший костюм. ... Поэтому теоретик — как портной». Я. Френкель, как указано в Филиппове (2000), стр. 131.
- ^ Пеллегрин, П. (2000). Бруншвиг, Дж.; Ллойд, GER (ред.). «Физика». Греческая мысль: Путеводитель по классическому знанию : 433–451.
- ^ Берггрен, Дж. Л. (2008). «Кодекс Архимеда» (PDF) . Уведомления AMS . 55 (8): 943–947.
- ↑ Питер Макамер «Галилео Галилей» — раздел 1 «Краткая биография», в Zalta EN, ред., Стэнфордская энциклопедия философии , весна 2010 г.
- ^ Энтони Г. Флю, Словарь философии , переиздание 2-е изд. (Нью-Йорк: St Martin's Press, 1984), стр. 129
- ↑ Энтони Г. Флю, Словарь философии , переиздание 2-е изд. (Нью-Йорк: St Martin's Press, 1984), стр. 89
- ^ Дейкстерхейс, Ф.Дж. (2008). Стевин, Гюйгенс и Голландская республика. Nieuw archive voor wiskunde, 5, стр. 100–107. https://research.utwente.nl/files/6673130/Dijksterhuis_naw5-2008-09-2-100.pdf
- ^ Андрессен, CD (2005) Гюйгенс: Человек, стоящий за принципом . Cambridge University Press: 6
- ^ Грегори, Джеймс (1668). Геометрия Pars Universalis. Музей Галилея : Патавии: типис Хередум Паули Фрамботти.
- ^ «Математические начала натуральной философии», Encyclopaedia Britannica , Лондон
- ^ ab Имре Лакатос, автор, Уорралл Дж. и Карри Г., редакторы, Методология научных исследовательских программ: Том 1: Философские статьи (Кембридж: Издательство Кембриджского университета, 1980), стр. 213–214, 220
- ^ Минковский, Герман (1908–1909), «Raum und Zeit» [Пространство и время], Physikalische Zeitschrift, 10: 75–88. На самом деле объединение пространства и времени подразумевалось сначала в работах Декарта, где пространство и время были представлены как оси координат, а затем в преобразованиях Лоренца, но его физическая интерпретация все еще была скрыта от здравого смысла.
- ^ Salmon WC & Wolters G, ред., Логика, язык и структура научных теорий (Питтсбург: University of Pittsburgh Press, 1994), стр. 125
- ^ Маккормах, Рассел (весна 1967 г.). «Анри Пуанкаре и квантовая теория». Isis . 58 (1): 37–55. doi :10.1086/350182. S2CID 120934561.
- ^ Айронс, FE (август 2001 г.). «Доказательство Пуанкаре 1911–12 гг. квантовой прерывности, интерпретируемое как применимое к атомам». American Journal of Physics . 69 (8): 879–84. Bibcode : 2001AmJPh..69..879I. doi : 10.1119/1.1356056.
Ссылки
- Заслоу, Эрик (2005), Физматика , arXiv : physics/0506153 , Bibcode : 2005physics...6153Z
Дальнейшее чтение
Общие работы
- Аллен, Джонт (2020), Приглашение к математической физике и ее истории , Springer, Bibcode : 2020imph.book.....A, ISBN 978-3-030-53758-6
- Курант, Ричард ; Гильберт, Дэвид (1989), Методы математической физики , том 1–2, Interscience Publishers
- Франсуаза, Жан П.; Набер, Грегори Л.; Цун, Цоу С. (2006), Энциклопедия математической физики , Elsevier, ISBN 978-0-1251-2660-1
- Йос, Георг ; Фримен, Айра М. (1987), Теоретическая физика (3-е изд.), Dover Publications, ISBN 0-486-65227-0
- Като, Тосио (1995), Теория возмущений линейных операторов (2-е изд.), Springer-Verlag, ISBN 3-540-58661-X
- Маргенау, Генри ; Мерфи, Джордж М. (2009), Математика физики и химии (2-е изд.), Young Press, ISBN 978-1444627473
- Масани, Песи Р. (1976–1986), Норберт Винер : Собрание сочинений с комментариями , том 1–4, The MIT Press
- Морзе, Филип М.; Фешбах , Герман (1999), Методы теоретической физики , том 1–2, McGraw Hill, ISBN 0-07-043316-X
- Тирринг, Уолтер Э. (1978–1983), Курс математической физики , том 1–4, Springer-Verlag
- Тихомиров, Владимир М. (1991–1993), Избранные труды А.Н. Колмогорова , том 1–3, Kluwer Academic Publishers
- Титчмарш, Эдвард К. (1985), Теория функций (2-е изд.), Oxford University Press
Учебники для бакалавриата
- Арфкен, Джордж Б .; Вебер, Ханс Дж.; Харрис, Фрэнк Э. (2013), Математические методы для физиков: всеобъемлющее руководство (7-е изд.), Academic Press, ISBN 978-0-12-384654-9, (Математические методы для физиков, Решения для математических методов для физиков (7-е изд.), archive.org)
- Баын, Сельчук Ш. (2018), Математические методы в науке и технике (2-е изд.), Wiley, ISBN 9781119425397
- Боас, Мэри Л. (2006), Математические методы в физических науках (3-е изд.), Wiley, ISBN 978-0-471-19826-0
- Бутков, Евгений (1968), Математическая физика , Эддисон-Уэсли
- Хассани, Садри (2009), Математические методы для студентов физики и смежных дисциплин , (2-е изд.), Нью-Йорк, Springer, eISBN 978-0-387-09504-2
- Джеффрис, Гарольд ; Свирлз Джеффрис, Берта (1956), Методы математической физики (3-е изд.), Cambridge University Press
- Марш, Адам (2018), «Математика для физики: иллюстрированное руководство», Contemporary Physics , 59 (3), World Scientific: 329, Bibcode : 2018ConPh..59..329N, doi : 10.1080/00107514.2018.1501430, ISBN 978-981-3233-91-1
- Мэтьюз, Джон ; Уокер, Роберт Л. (1970), Математические методы физики (2-е изд.), WA Benjamin, ISBN 0-8053-7002-1
- Менцель, Дональд Х. (1961), Математическая физика , Dover Publications, ISBN 0-486-60056-4
- Райли, Кен Ф.; Хобсон, Майкл П.; Бенс, Стивен Дж. (2006), Математические методы в физике и инженерии (3-е изд.), Cambridge University Press, ISBN 978-0-521-86153-3
- Stakgold, Ivar (2000), Краевые задачи математической физики , том 1-2., Общество промышленной и прикладной математики, ISBN 0-89871-456-7
- Старкович, Стивен П. (2021), Структуры математической физики: Введение , Springer, Bibcode :2021smpa.book.....S, ISBN 978-3-030-73448-0
Учебники для аспирантуры
- Бланшар, Филипп ; Брюнинг, Эрвин (2015), Математические методы в физике: распределения, операторы гильбертова пространства, вариационные методы и приложения в квантовой физике (2-е изд.), Springer, Bibcode : 2015mmpd.book.....B, ISBN 978-3-319-14044-5
- Кэхилл, Кевин (2019), Физическая математика (2-е изд.), Cambridge University Press, ISBN 978-1-108-47003-2
- Герох, Роберт (1985), математическая физика , издательство Чикагского университета, ISBN 0-226-28862-5
- Хассани, Садри (2013), Математическая физика: Современное введение в ее основы (2-е изд.), Springer-Verlag, Bibcode :2013mpmi.book.....H, ISBN 978-3-319-01194-3
- Марате, Кишор (2010), Темы по физической математике , Springer-Verlag, ISBN 978-1-84882-938-1
- Мильштейн, Григорий Н.; Третьяков, Михаил В. (2021), Стохастические числа для математической физики (2-е изд.), Springer, ISBN 978-3-030-82039-8
- Рид, Майкл С.; Саймон , Барри (1972–1981), Методы современной математической физики , том 1–4, Academic Press
- Рихтмайер, Роберт Д. (1978–1981), Принципы высшей математической физики , том 1-2., Springer-Verlag
- Рудольф, Герд; Шмидт, Маттиас (2013–2017), Дифференциальная геометрия и математическая физика , том 1-2, Springer
- Серов, Валерий (2017), Ряды Фурье, Преобразование Фурье и их приложения к математической физике , Springer, ISBN 978-3-319-65261-0
- Саймон, Барри (2015), Комплексный курс анализа , том 1-5, Американское математическое общество
- Stakgold, Ivar ; Holst, Michael (2011), Функции Грина и граничные задачи (3-е изд.), Wiley, ISBN 978-0-470-60970-5
- Стоун, Майкл; Голдбарт, Пол (2009), «Математика для физики: путеводитель для аспирантов», Physics Today , 62 (10), Cambridge University Press: 57, Bibcode : 2009PhT....62j..57S, doi : 10.1063/1.3248483, ISBN 978-0-521-85403-0
- Секереш, Питер (2004), Курс современной математической физики: группы, гильбертово пространство и дифференциальная геометрия , Cambridge University Press, ISBN 978-0-521-53645-5
- Тейлор, Майкл Э. (2011), Уравнения в частных производных , том 1-3 (2-е изд.), Springer.
- Уиттекер, Эдмунд Т.; Уотсон , Джордж Н. (1950), Курс современного анализа: Введение в общую теорию бесконечных процессов и аналитических функций с учетом главных трансцендентных функций (4-е изд.), Cambridge University Press
Специализированные тексты по классической физике
- Абрахам, Ральф ; Марсден, Джерролд Э. (2008), Основы механики: математическое изложение классической механики с введением в качественную теорию динамических систем (2-е изд.), AMS Chelsea Publishing, ISBN 978-0-8218-4438-0
- Адам, Джон А. (2017), Лучи, волны и рассеяние: темы классической математической физики , Princeton University Press., ISBN 978-0-691-14837-3
- Арнольд, Владимир И. (1997), Математические методы классической механики (2-е изд.), Springer-Verlag, ISBN 0-387-96890-3
- Блум, Фредерик (1993), Математические проблемы классической нелинейной электромагнитной теории , CRC Press, ISBN 0-582-21021-6
- Бойер, Франк; Фабри, Пьер (2013), Математические инструменты для изучения несжимаемых уравнений Навье-Стокса и связанных с ними моделей , Springer, ISBN 978-1-4614-5974-3
- Колтон, Дэвид; Кресс, Райнер (2013), Методы интегральных уравнений в теории рассеяния , Общество промышленной и прикладной математики, ISBN 978-1-611973-15-0
- Ciarlet, Philippe G. (1988–2000), Математическая эластичность , том 1–3, Elsevier
- Гальди, Джованни П. (2011), Введение в математическую теорию уравнений Навье-Стокса: стационарные задачи (2-е изд.), Springer, ISBN 978-0-387-09619-3
- Хансон, Джордж У.; Яковлев, Александр Б. (2002), Операторная теория электромагнетизма: Введение , Springer, ISBN 978-1-4419-2934-1
- Кирш, Андреас; Хеттлих, Франк (2015), Математическая теория гармонических во времени уравнений Максвелла: методы расширения, интегральные и вариационные методы , Springer, Bibcode :2015mttm.book.....K, ISBN 978-3-319-11085-1
- Кнауф, Андреас (2018), Математическая физика: Классическая механика , Springer, ISBN 978-3-662-55772-3
- Лехнер, Курт (2018), Классическая электродинамика: современная перспектива , Springer, ISBN 978-3-319-91808-2
- Марсден, Джерролд Э.; Ратиу , Тюдор С. (1999), Введение в механику и симметрию: базовое изложение классических механических систем (2-е изд.), Springer, ISBN 978-1-4419-3143-6
- Мюллер, Клаус (1969), Основы математической теории электромагнитных волн , Springer-Verlag, ISBN 978-3-662-11775-0
- Рамм, Александр Г. (2018), Рассеивание препятствиями и потенциалами , World Scientific, ISBN 9789813220966
- Роуч, Гэри Ф.; Стратис, Иоаннис Г.; Яннакопулос, Атанасиос Н. (2012), Математический анализ детерминированных и стохастических задач в сложных электромагнитных средах , Princeton University Press, Bibcode : 2012mads.book.....R, ISBN 978-0-691-14217-3
Специализированные тексты по современной физике
- Баез, Джон К.; Муниаин, Хавьер П. (1994), Калибровочные поля, узлы и гравитация , World Scientific, ISBN 981-02-2034-0
- Бланк, Иржи; Экснер, Павел ; Гавличек, Милослав (2008), Операторы гильбертового пространства в квантовой физике (2-е изд.), Springer, ISBN 978-1-4020-8869-8
- Энгель, Эберхард; Дрейцлер, Райнер М. (2011), Теория функционала плотности: продвинутый курс , Springer-Verlag, ISBN 978-3-642-14089-1
- Глимм, Джеймс ; Джаффе, Артур (1987), Квантовая физика: точка зрения функционального интеграла (2-е изд.), Springer-Verlag, ISBN 0-387-96477-0
- Хааг, Рудольф (1996), Локальная квантовая физика: поля, частицы, алгебры (2-е изд.), Springer-Verlag, ISBN 3-540-61049-9
- Холл, Брайан С. (2013), Квантовая теория для математиков , Springer, Bibcode :2013qtm..book.....H, ISBN 978-1-4614-7115-8
- Гамильтон, Марк Дж. Д. (2017), Математическая теория калибровок: с приложениями к Стандартной модели физики элементарных частиц , Springer, Bibcode :2017mgta.book.....H, ISBN 978-3-319-68438-3
- Хокинг, Стивен У .; Эллис, Джордж Ф.Р. (1973), Крупномасштабная структура пространства-времени , Cambridge University Press, ISBN 0-521-20016-4
- Джекив, Роман (1995), Разнообразные темы в теоретической и математической физике , World Scientific, ISBN 9810216963
- Ландсман, Клаас (2017), Основы квантовой теории: от классических концепций к операторным алгебрам , Springer, Bibcode :2017fqtf.book.....L, ISBN 978-3-319-51776-6
- Моретти, Вальтер (2017), Спектральная теория и квантовая механика: математические основы квантовых теорий, симметрии и введение в алгебраическую формулировку, Unitext, т. 110 (2-е изд.), Springer, Bibcode : 2017stqm.book.....M, doi : 10.1007/978-3-319-70706-8, ISBN 978-3-319-70705-1, S2CID 125121522
- Роберт, Дидье; Комбескюр, Моник (2021), Когерентные состояния и их применение в математической физике (2-е изд.), Springer, ISBN 978-3-030-70844-3
- Тасаки, Хэл (2020), Физика и математика квантовых многочастичных систем, Springer, ISBN 978-3-030-41265-4, OCLC 1154567924
- Тешль, Джеральд (2009), Математические методы в квантовой механике: с приложениями к операторам Шредингера, Американское математическое общество, ISBN 978-0-8218-4660-5
- Тирринг, Уолтер Э. (2002), Квантовая математическая физика: атомы, молекулы и большие системы (2-е изд.), Springer-Verlag, Bibcode :2002qmpa.book.....T, ISBN 978-3-642-07711-1
- фон Нейман, Джон (2018), Математические основы квантовой механики , Princeton University Press, ISBN 978-0-691-17856-1
- Вейль, Герман (2014), Теория групп и квантовая механика , Martino Fine Books, ISBN 978-1614275800
- Ynduráin, Francisco J. (2006), Теория кварковых и глюонных взаимодействий (4-е изд.), Springer, ISBN 978-3642069741
- Зейдлер, Эберхард (2006–2011), Квантовая теория поля: мост между математиками и физиками , том 1-3, Springer


