Усеченные 8-симплексы

8-симплекс	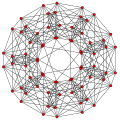Усеченный 8-симплекс	Выпрямленный 8-симплекс
Квадритрукированный 8-симплекс	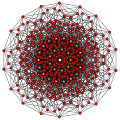Три-усеченный 8-симплекс	Усеченный 8-симплекс
Ортогональные проекции в плоскости Коксетера A 8

В восьмимерной геометрии усеченный 8-симплекс — это выпуклый однородный 8-многогранник , являющийся усечением правильного 8-симплекса .

Существует четыре уникальные степени усечения. Вершины усеченного 8-симплекса расположены парами на ребре 8-симплекса. Вершины битусеченного 8-симплекса расположены на треугольных гранях 8-симплекса. Вершины триусеченного 8-симплекса расположены внутри тетраэдрических ячеек 8- симплекса .

Усеченный 8-симплекс
Тип	однородный 8-многогранник
Символ Шлефли	т{3 7 }
Диаграммы Коксетера-Дынкина
7-гранный
6-гранный
5-гранный
4-х гранный
Клетки
Лица
Края	288
Вершины	72
Вершинная фигура	( )в{3,3,3,3,3}
Группа Коксетера	А 8 , [3 7 ], заказ 362880
Характеристики	выпуклый

• Усеченный эннеазеттон (Акроним: тенэ) (Джонатан Бауэрс) ^[1]

Декартовы координаты вершин усеченного 8-симплекса проще всего расположить в 9-пространстве как перестановки (0,0,0,0,0,0,0,1,2). Эта конструкция основана на гранях усеченного 9-ортоплекса.

ортографические проекции

Самолет Коксетера ​	А 8	А 7	А 6	А 5
График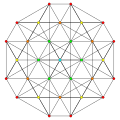
Диэдральная симметрия	[9]	[8]	[7]	[6]
Самолет Коксетера​	А 4	А 3	А 2
График
Диэдральная симметрия	[5]	[4]	[3]

Усеченный 8-симплекс
Тип	однородный 8-многогранник
Символ Шлефли	2т{3 7 }
Диаграммы Коксетера-Дынкина
7-гранный
6-гранный
5-гранный
4-х гранный
Клетки
Лица
Края	1008
Вершины	252
Вершинная фигура	{ }v{3,3,3,3}
Группа Коксетера	А 8 , [3 7 ], заказ 362880
Характеристики	выпуклый

• Усеченный эннеазеттон (сокращение: batene) (Джонатан Бауэрс) ^[2]

Декартовы координаты вершин битусеченного 8-симплекса проще всего расположить в 9-пространстве как перестановки (0,0,0,0,0,0,1,2,2). Эта конструкция основана на гранях битусеченного 9-ортоплекса.

ортографические проекции

Самолет Коксетера ​	А 8	А 7	А 6	А 5
График
Диэдральная симметрия	[9]	[8]	[7]	[6]
Самолет Коксетера​	А 4	А 3	А 2
График
Диэдральная симметрия	[5]	[4]	[3]

три-усеченный 8-симплекс
Тип	однородный 8-многогранник
Символ Шлефли	3т{3 7 }
Диаграммы Коксетера-Дынкина
7-гранный
6-гранный
5-гранный
4-х гранный
Клетки
Лица
Края	2016
Вершины	504
Вершинная фигура	{3}в{3,3,3}
Группа Коксетера	А 8 , [3 7 ], заказ 362880
Характеристики	выпуклый

• Три-усеченный эннеазеттон (Акроним: татене) (Джонатан Бауэрс) ^[3]

Декартовы координаты вершин триусеченного 8-симплекса проще всего расположить в 9-пространстве как перестановки (0,0,0,0,0,1,2,2,2). Эта конструкция основана на гранях триусеченного 9-ортоплекса.

ортографические проекции

Самолет Коксетера ​	А 8	А 7	А 6	А 5
График
Диэдральная симметрия	[9]	[8]	[7]	[6]
Самолет Коксетера​	А 4	А 3	А 2
График
Диэдральная симметрия	[5]	[4]	[3]

Квадритрукированный 8-симплекс
Тип	однородный 8-многогранник
Символ Шлефли	4т{3 7 }
Диаграммы Коксетера-Дынкина	или
6-гранный	18 3т{3,3,3,3,3,3}
7-гранный
5-гранный
4-х гранный
Клетки
Лица
Края	2520
Вершины	630
Вершинная фигура	{3,3}в{3,3}
Группа Коксетера	А 8 , [[3 7 ]], заказ 725760
Характеристики	выпуклый , изотопный

Квадроусеченный 8-симплекс — изотопный многогранник, построенный из 18 триусеченных 7-симплексных граней .

• Октадеказеттон (18-гранный 8-многогранник) (Акроним: be) (Джонатан Бауэрс) ^[4]

Декартовы координаты вершин квадриусеченного 8-симплекса проще всего расположить в 9-пространстве как перестановки (0,0,0,0,1,2,2,2,2). Эта конструкция основана на гранях квадриусеченного 9-ортоплекса.

ортографические проекции

Самолет Коксетера ​	А 8	А 7	А 6	А 5
График
Диэдральная симметрия	[[9]] = [18]	[8]	[[7]] = [14]	[6]
Самолет Коксетера​	А 4	А 3	А 2
График
Диэдральная симметрия	[[5]] = [10]	[4]	[[3]] = [6]

Изотопные однородные усеченные симплексы

Размыто.	2	3	4	5	6	7	8
Имя Коксетер	Шестиугольник = т{3} = {6}	Октаэдр = г{3,3} = {3 1,1 } = {3,4} ${\displaystyle \left\{{\begin{array}{l}3\\3\end{array}}\right\}}$	Декахорон 2т{3 3 }	Додекатерон 2r{3 4 } = {3 2,2 } ${\displaystyle \left\{{\begin{array}{l}3,3\\3,3\end{array}}\right\}}$	Тетрадекапетон 3т{3 5 }	Гексадекаэкзон 3r{3 6 } = {3 3,3 } ${\displaystyle \left\{{\begin{array}{l}3,3,3\\3,3,3\end{array}}\right\}}$	Октадеказеттон 4т{3 7 }
Изображения
Вершинная фигура	( )∨( )	{ }×{ }	{ }∨{ }	{3}×{3}	{3}∨{3}	{3,3}×{3,3}	{3,3}∨{3,3}
Грани		{3}	т{3,3}	г{3,3,3}	2т{3,3,3,3}	2р{3,3,3,3,3}	3т{3,3,3,3,3,3}
Как пересекающиеся двойные симплексы	∩	∩	∩	∩	∩	∩	∩

Этот многогранник является одним из 135 однородных 8-мерных многогранников с симметрией A ₈ .

Многогранники A8
т 0	т 1	т 2	т 3	т 01	т 02	т 12	т 03	т 13	т 23	т 04	т 14	т 24	т 34	т 05
т 15	т 25	т 06	т 16	т 07	т 012	т 013	т 023	т 123	т 014	т 024	т 124	т 034	т 134	т 234
т015	т025	т 125	т035	т 135	т235	т045	т 145	т016	т026	т126	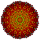т036	т136	т046	т056
т017	т027	т037	т 0123	т 0124	т 0134	т 0234	т 1234	т0125	т0135	т0235	т 1235	т0145	т0245	т 1245
т0345	т 1345	т 2345	т0126	т0136	т0236	т1236	т0146	т0246	т1246	т0346	т1346	т0156	т0256	т1256
т0356	т0456	т0127	т0137	т0237	т0147	т0247	т0347	т0157	т0257	т0167	т 01234	т01235	т01245	т01345
т02345	т 12345	т01236	т01246	т01346	т02346	т12346	т01256	т01356	т02356	т12356	т01456	т02456	т03456	т01237
т01247	т01347	т02347	т01257	т01357	т02357	т01457	т01267	т01367	т012345	т012346	т012356	т012456	т013456	т023456
т123456	т012347	т012357	т012457	т013457	т023457	т012367	т012467	т013467	т012567	т0123456	т0123457	т0123467	т0123567	т 01234567

• HSM Коксетер :
  • HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973 г.
  • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
    • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
• Норман Джонсон Однородные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
• Клитцинг, Ричард. «8D однородные многогранники (полизеттовые)».х3х3о3о3о3о3о3о - тэнэ, о3х3х3о3о3о3о3о - батэне, о3о3х3х3о3о3о3о - татене, о3о3о3х3х3о3о3о - быть

• Многогранники различных размерностей
• Многомерный глоссарий